Cuadrícula regular
Este artículo necesita citas adicionales para su verificación . ( diciembre de 2009 ) |
Una cuadrícula regular es una teselación del espacio euclidiano n -dimensional mediante paraleletotopos congruentes (por ejemplo, ladrillos ). [1] Su opuesto es la cuadrícula irregular .
Las cuadrículas de este tipo aparecen en papel cuadriculado y pueden utilizarse en análisis de elementos finitos , métodos de volumen finito , métodos de diferencias finitas y, en general, para la discretización de espacios de parámetros. Dado que las derivadas de las variables de campo pueden expresarse convenientemente como diferencias finitas, [2] las cuadrículas estructuradas aparecen principalmente en métodos de diferencias finitas. Las cuadrículas no estructuradas ofrecen más flexibilidad que las cuadrículas estructuradas y, por lo tanto, son muy útiles en los métodos de elementos finitos y de volumen finito.
Cada celda de la cuadrícula puede ser direccionada por el índice (i, j) en dos dimensiones o (i, j, k) en tres dimensiones, y cada vértice tiene coordenadas en 2D o en 3D para algunos números reales dx , dy y dz que representan el espaciado de la cuadrícula.
Cuadrículas relacionadas
Una cuadrícula cartesiana es un caso especial donde los elementos son cuadrados unitarios o cubos unitarios , y los vértices son puntos en la red entera .
Una cuadrícula rectilínea es una teselación de rectángulos o cuboides rectangulares (también conocidos como paralelepípedos rectangulares ) que, en general, no son todos congruentes entre sí. Las celdas pueden seguir estando indexadas por números enteros como se indicó anteriormente, pero la asignación de índices a coordenadas de vértices es menos uniforme que en una cuadrícula regular. Un ejemplo de una cuadrícula rectilínea que no es regular aparece en papel cuadriculado de escala logarítmica .
Una cuadrícula sesgada es una teselación de paralelogramos o paralelepípedos . (Si las longitudes unitarias son todas iguales, se trata de una teselación de rombos o romboedros ).
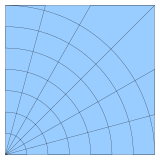
Una cuadrícula curvilínea o cuadrícula estructurada es una cuadrícula con la misma estructura combinatoria que una cuadrícula regular, en la que las celdas son cuadriláteros o cuboides [generales] , en lugar de rectángulos o cuboides rectangulares.
Véase también
- Sistema de coordenadas cartesianas : sistema de coordenadas más común (geometría)
- Red de enteros : grupo reticular en el espacio euclidiano cuyos puntos son n-tuplas de enteros
- Cuadrícula no estructurada : una cuadrícula no estructurada (o irregular) es una teselación de una parte del plano euclidiano.
- Discretización : proceso de transferencia de funciones continuas a contrapartes discretas.
Referencias
- ^ Uznanski, Dan. "Grid". De MathWorld--A Wolfram Web Resource, creado por Eric W. Weisstein . Consultado el 25 de marzo de 2012 .
- ^ JF Thompson, B. K. Soni y NP Weatherill (1998). Manual de generación de redes. CRC-Press. ISBN 978-0-8493-2687-5.
 | Este artículo relacionado con la geometría elemental es un esbozo . Puedes ayudar a Wikipedia expandiéndolo. |
