Computación cuántica superconductora
Implementación de la computación cuántica

La computación cuántica superconductora es una rama de la física del estado sólido y la computación cuántica que implementa circuitos electrónicos superconductores utilizando cúbits superconductores como átomos artificiales o puntos cuánticos . Para los cúbits superconductores, los dos estados lógicos son el estado fundamental y el estado excitado , denotados respectivamente. [1] La investigación en computación cuántica superconductora la llevan a cabo empresas como Google , [2] IBM , [3] IMEC , [4] BBN Technologies , [5] Rigetti , [6] e Intel . [7] Muchas QPU ( unidades de procesamiento cuántico o chips cuánticos) desarrolladas recientemente utilizan una arquitectura superconductora. | gramo ⟩  y  | mi ⟩ {\displaystyle |g\rangle {\text{ y }}|e\rangle }

A partir de mayo de 2016 , se demostraron [actualizar]hasta 9 qubits totalmente controlables en la matriz 1D , [8] y hasta 16 en la arquitectura 2D. [3] En octubre de 2019, el grupo Martinis , asociado con Google , publicó un artículo que demostraba una novedosa supremacía cuántica , utilizando un chip compuesto por 53 qubits superconductores. [9]

Fondo

Los modelos de computación clásica se basan en implementaciones físicas consistentes con las leyes de la mecánica clásica . [10] Las descripciones clásicas son precisas solo para sistemas específicos que constan de un número relativamente grande de átomos. La mecánica cuántica proporciona una descripción más general de la naturaleza . La computación cuántica estudia las aplicaciones de los fenómenos cuánticos más allá del alcance de la aproximación clásica, con el propósito de realizar el procesamiento y la comunicación de información cuántica . Existen varios modelos de computación cuántica, pero los modelos más populares incorporan conceptos de qubits y puertas cuánticas (o computación cuántica superconductora basada en puertas).

Los superconductores se implementan debido a que a bajas temperaturas tienen una conductividad infinita y una resistencia cero. Cada cúbit se construye utilizando circuitos semiconductores con un circuito LC : un condensador y un inductor. [ cita requerida ]

Los condensadores e inductores superconductores se utilizan para producir un circuito resonante que casi no disipa energía, ya que el calor puede alterar la información cuántica. Los circuitos resonantes superconductores son una clase de átomos artificiales que se pueden utilizar como qubits. Las implementaciones teóricas y físicas de los circuitos cuánticos son muy diferentes. La implementación de un circuito cuántico tiene su propio conjunto de desafíos y debe cumplir con los criterios de DiVincenzo , condiciones propuestas por el físico teórico David P DiVincenzo, [11] que es un conjunto de criterios para la implementación física de la computación cuántica superconductora, donde los cinco criterios iniciales aseguran que la computadora cuántica esté en línea con los postulados de la mecánica cuántica y los dos restantes pertenecen a la retransmisión de esta información a través de una red. [ cita requerida ]

Mapeamos los estados fundamental y excitado de estos átomos al estado 0 y 1, ya que estos son valores de energía discretos y distintos y, por lo tanto, está en línea con los postulados de la mecánica cuántica. Sin embargo, en una construcción de este tipo, un electrón puede saltar a múltiples otros estados de energía y no estar confinado a nuestro estado excitado; por lo tanto, es imperativo que el sistema se limite a verse afectado solo por fotones con la diferencia de energía requerida para saltar del estado fundamental al estado excitado. [12] Sin embargo, esto deja un problema importante: requerimos un espaciado desigual entre nuestros niveles de energía para evitar que los fotones con la misma energía provoquen transiciones entre pares de estados vecinos. Las uniones Josephson son elementos superconductores con una inductancia no lineal, que es de importancia crítica para la implementación de qubits. [12] El uso de este elemento no lineal en el circuito superconductor resonante produce espaciamientos desiguales entre los niveles de energía. [ cita requerida ]

Cubits

Un qubit es una generalización de un bit (un sistema con dos estados posibles ) capaz de ocupar una superposición cuántica de ambos estados. Una compuerta cuántica, por otro lado, es una generalización de una compuerta lógica que describe la transformación de uno o más qubits una vez que se aplica una compuerta dado su estado inicial. La implementación física de qubits y compuertas es un desafío por la misma razón que los fenómenos cuánticos son difíciles de observar en la vida cotidiana dada la escala diminuta en la que ocurren. Un enfoque para lograr computadoras cuánticas es mediante la implementación de superconductores mediante los cuales los efectos cuánticos son observables macroscópicamente , aunque al precio de temperaturas de operación extremadamente bajas .

Superconductores

A diferencia de los conductores típicos, los superconductores poseen una temperatura crítica en la que la resistividad cae en picado hasta casi cero y la conductividad aumenta drásticamente. En los superconductores, los portadores de carga básicos son pares de electrones (conocidos como pares de Cooper ), en lugar de fermiones individuales como los que se encuentran en los conductores típicos. [13] Los pares de Cooper están débilmente ligados y tienen un estado de energía inferior al de la energía de Fermi . Los electrones que forman pares de Cooper poseen un momento y un espín iguales y opuestos, de modo que el espín total del par de Cooper es un espín entero . Por tanto, los pares de Cooper son bosones . Dos de estos superconductores que se han utilizado en modelos de cúbits superconductores son el niobio y el tantalio , ambos superconductores de banda d. [14]

Condensados ​​de Bose-Einstein

Una vez enfriados hasta casi el cero absoluto , una colección de bosones colapsa en su estado cuántico de energía más baja (el estado fundamental ) para formar un estado de la materia conocido como condensado de Bose-Einstein . A diferencia de los fermiones, los bosones pueden ocupar el mismo nivel de energía cuántica (o estado cuántico ) y no obedecen al principio de exclusión de Pauli . Clásicamente, el condensado de Bose-Einstein puede conceptualizarse como múltiples partículas que ocupan la misma posición en el espacio y tienen el mismo momento . Debido a que las fuerzas interactivas entre los bosones se minimizan, los condensados ​​de Bose-Einstein actúan efectivamente como un superconductor. Por lo tanto, los superconductores se implementan en la computación cuántica porque poseen una conductividad casi infinita y una resistencia cercana a cero . Las ventajas de un superconductor sobre un conductor típico, entonces, son dobles en el sentido de que los superconductores pueden, en teoría, transmitir señales casi instantáneamente y funcionar infinitamente sin pérdida de energía. La perspectiva de hacer realidad las computadoras cuánticas superconductoras se torna aún más prometedora considerando el reciente desarrollo por parte de la NASA del Laboratorio de Átomos Fríos en el espacio exterior, donde los Condensados ​​de Bose-Einstein se logran y sostienen más fácilmente (sin disipación rápida) durante períodos más largos sin las limitaciones de la gravedad . [15]

Circuitos eléctricos

En cada punto de un circuito electrónico superconductor (una red de elementos eléctricos ), la función de onda condensada que describe el flujo de carga está bien definida por una amplitud de probabilidad compleja . En los circuitos eléctricos conductores típicos, esta misma descripción es válida para los portadores de carga individuales , excepto que las diversas funciones de onda se promedian en el análisis macroscópico, lo que hace imposible observar los efectos cuánticos. La función de onda condensada se vuelve útil para permitir el diseño y la medición de efectos cuánticos macroscópicos. De manera similar a los niveles de energía atómica discretos en el modelo de Bohr , solo un número discreto de cuantos de flujo magnético pueden penetrar un bucle superconductor. En ambos casos, la cuantificación resulta de la continuidad de amplitud compleja . A diferencia de las implementaciones microscópicas de las computadoras cuánticas (como los átomos o los fotones ), los parámetros de los circuitos superconductores se diseñan estableciendo valores (clásicos) para los elementos eléctricos que los componen, como por ejemplo ajustando la capacitancia o la inductancia .

Para obtener una descripción mecánico cuántica de un circuito eléctrico, se requieren algunos pasos. En primer lugar, todos los elementos eléctricos deben describirse mediante la amplitud y la fase de la función de onda condensada en lugar de mediante descripciones macroscópicas de corriente y voltaje estrechamente relacionadas que se utilizan para los circuitos clásicos. Por ejemplo, el cuadrado de la amplitud de la función de onda en cualquier punto arbitrario del espacio corresponde a la probabilidad de encontrar un portador de carga allí. Por lo tanto, la amplitud al cuadrado corresponde a una distribución de carga clásica. El segundo requisito para obtener una descripción mecánico cuántica de un circuito eléctrico es que se apliquen las leyes de circuitos de Kirchhoff generalizadas en cada nodo de la red de circuitos para obtener las ecuaciones de movimiento del sistema . Finalmente, estas ecuaciones de movimiento deben reformularse a la mecánica lagrangiana de modo que se derive un hamiltoniano cuántico que describa la energía total del sistema.

Tecnología

Fabricación

Los dispositivos de computación cuántica superconductores se diseñan típicamente en el espectro de radiofrecuencia , se enfrían en refrigeradores de dilución por debajo de 15  mK y se abordan con instrumentos electrónicos convencionales, por ejemplo, sintetizadores de frecuencia y analizadores de espectro . Las dimensiones típicas caen en el rango de micrómetros, con resolución submicrométrica, lo que permite el diseño conveniente de un sistema hamiltoniano con tecnología de circuito integrado bien establecida . La fabricación de qubits superconductores sigue un proceso que involucra litografía , deposición de metal, grabado y oxidación controlada como se describe en. [16] Los fabricantes continúan mejorando la vida útil de los qubits superconductores y han realizado mejoras significativas desde principios de la década de 2000. [16] : 4 

Cruces de Josephson

Una única unión Josephson donde C es una fina capa de aislante y A y B son corrientes (superconductoras) con funciones de onda no equivalentes

Un atributo distintivo de los circuitos cuánticos superconductores es el uso de uniones Josephson . Las uniones Josephson son un elemento eléctrico que no existe en los conductores normales . Recordemos que una unión es una conexión débil entre dos conductores de cable (en este caso, un cable superconductor) a cada lado de una fina capa de material aislante de solo unos pocos átomos de espesor, generalmente implementada mediante la técnica de evaporación de sombra . El dispositivo de unión Josephson resultante exhibe el efecto Josephson por el cual la unión produce una supercorriente . A la derecha se muestra una imagen de una sola unión Josephson. La función de onda de condensado en los dos lados de la unión está débilmente correlacionada, lo que significa que se les permite tener diferentes fases superconductoras. Esta distinción de no linealidad contrasta con el cable superconductor continuo para el cual la función de onda a través de la unión debe ser continua . El flujo de corriente a través de la unión se produce por efecto túnel cuántico , que parece "tunelizarse" instantáneamente de un lado de la unión al otro. Este fenómeno de efecto túnel es exclusivo de los sistemas cuánticos. Por lo tanto, la tunelización cuántica se utiliza para crear inductancia no lineal, esencial para el diseño de qubits, ya que permite un diseño de osciladores anarmónicos para los cuales los niveles de energía se discretizan (o cuantifican ) con un espaciado no uniforme entre niveles de energía, denotado . [1] Por el contrario, el oscilador armónico cuántico no se puede utilizar como un qubit, ya que no hay forma de abordar solo dos de sus estados, dado que el espaciado entre cada nivel de energía y el siguiente es exactamente el mismo. Δ mi {\displaystyle \Delta E}

Arquetipos de qubits

Los tres arquetipos primarios de cúbits superconductores son los cúbits de fase , carga y flujo . Existen muchas hibridaciones de estos arquetipos, incluidos el fluxonio, [17] transmon , [18] Xmon, [19] y quantronio. [20] Para cualquier implementación de cúbits, los estados cuánticos lógicos se asignan a diferentes estados del sistema físico (normalmente a niveles de energía discretos o sus superposiciones cuánticas ). Cada uno de los tres arquetipos posee un rango distinto de relación entre la energía de Josephson y la energía de carga. La energía de Josephson se refiere a la energía almacenada en las uniones de Josephson cuando pasa corriente a través de ellas, y la energía de carga es la energía necesaria para que un par de Cooper cargue la capacitancia total de la unión. [21] La energía de Josephson se puede escribir como { | 0 ⟩ , | 1 ⟩ } {\displaystyle \{|0\rangle ,|1\rangle \}}

Gráfico de varios arquetipos de cúbits superconductores según su relación de energía de Josephson con la energía de carga, con una leyenda a la derecha. [22] El gráfico superior izquierdo ilustra un circuito eléctrico unimon. [22]
tú yo = − I 0 Φ 0 2 π porque ⁡ del {\displaystyle U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}\cos \delta } ,

donde es el parámetro de corriente crítico de la unión Josephson, es el cuanto de flujo (superconductor) y es la diferencia de fase a través de la unión. [21] Nótese que el término indica no linealidad de la unión Josephson. [21] La energía de carga se escribe como I 0 {\displaystyle I_{0}} Φ 0 = yo 2 mi {\displaystyle \textstyle \Phi _{0}={\frac {h}{2e}}} del {\estilo de visualización \delta} do o s del {\displaystyle cos\delta}

mi do = mi 2 2 do {\displaystyle E_{C}={\frac {e^{2}}{2C}}} ,

donde es la capacitancia de la unión y es la carga del electrón. [21] De los tres arquetipos, los qubits de fase permiten que la mayoría de los pares de Cooper pasen a través de la unión, seguidos por los qubits de flujo, y los qubits de carga permiten la menor cantidad. do {\estilo de visualización C} mi {\estilo de visualización e}

Cubit de fase

El cúbit de fase posee una relación de energía de Josephson a carga del orden de magnitud . Para los cúbits de fase, los niveles de energía corresponden a diferentes amplitudes de oscilación de carga cuántica a través de una unión Josephson, donde la carga y la fase son análogas al momento y la posición respectivamente, como análogas a un oscilador armónico cuántico . Nótese que en este contexto la fase es el argumento complejo de la función de onda superconductora (también conocida como el parámetro de orden superconductor ), no la fase entre los diferentes estados del cúbit. 10 6 {\estilo de visualización 10^{6}}

La imagen más a la izquierda muestra un circuito superconductor de fluxonio que consiste en una colección de uniones Josephson de área más grande y una unión Josephson de área más pequeña, como se muestra mediante un microscopio electrónico. [23] La imagen superior derecha muestra los componentes del circuito de fluxonio y la imagen inferior derecha muestra una unión Josephson de área más pequeña. [23]

cúbit de flujo

El cúbit de flujo (también conocido como cúbit de corriente persistente) posee una relación entre la energía de Josephson y la energía de carga del orden de magnitud . En el caso de los cúbits de flujo, los niveles de energía corresponden a diferentes números enteros de cuantos de flujo magnético atrapados en un anillo superconductor. 10 {\estilo de visualización 10}

Fluxonio

Los qubits de fluxonio son un tipo específico de qubit de flujo cuya unión Josephson está desviada por un inductor lineal de donde . [24] En la práctica, el inductor lineal suele implementarse mediante una matriz de uniones Josephson que se compone de una gran cantidad (puede ser a menudo ) de uniones Josephson de gran tamaño conectadas en serie. Bajo esta condición, el hamiltoniano de un fluxonio se puede escribir como: mi Yo ≫ mi yo {\displaystyle E_{J}\gg E_{L}} mi yo = ( ℏ / 2 mi ) 2 / yo {\displaystyle E_{L}=(\hbar /2e)^{2}/L} norte > 100 {\displaystyle N>100}

yo ^ = 4 mi do norte ^ 2 + 1 2 mi yo ( ϕ ^ − ϕ mi incógnita a ) 2 − mi Yo porque ⁡ ϕ ^ {\displaystyle {\hat {H}}=4E_{C}{\hat {n}}^{2}+{\frac {1}{2}}E_{L}({\hat {\phi }} -\phi _{\mathrm {ext} })^{2}-E_{J}\cos {\hat {\phi }}} .

Una propiedad importante del qubit de fluxonio es su mayor vida útil en el punto óptimo de flujo medio, que puede superar 1 milisegundo. [24] [25] Otra ventaja crucial del qubit de fluxonio sesgado en el punto óptimo es su gran anarmonicidad, que permite un rápido control local de microondas y mitiga los problemas de aglomeración espectral, lo que conduce a una mejor escalabilidad. [26] [27]

Carga de qubit

El cúbit de carga, también conocido como caja de pares de Cooper , posee una relación de energía de Josephson a energía de carga del orden de magnitud . Para los cúbits de carga, los diferentes niveles de energía corresponden a un número entero de pares de Cooper en una isla superconductora (una pequeña área superconductora con un número controlable de portadores de carga). [28] De hecho, el primer cúbit realizado experimentalmente fue la caja de pares de Cooper, lograda en 1999. [29] < 1 {\estilo de visualización <1}

Un dispositivo que consta de cuatro qubits transmon superconductores , cuatro buses cuánticos y cuatro resonadores de lectura fabricados por IBM y publicados en npj Quantum Information en enero de 2017 [30]

Transmón

Los transmones son un tipo especial de cúbit con un condensador derivado diseñado específicamente para mitigar el ruido . El modelo de cúbit transmones se basó en la caja de pares de Cooper [31] (ilustrada en la tabla anterior en la fila uno, columna uno). También fue el primer cúbit en demostrar la supremacía cuántica . [32] La mayor relación entre la energía de Josephson y la energía de carga mitiga el ruido. Se pueden acoplar dos transmones utilizando un condensador de acoplamiento . [1] Para este sistema de 2 cúbits, el hamiltoniano se escribe

yo ^ = ℏ Yo 2 ( σ 1 incógnita σ 2 incógnita + σ 1 y σ 2 y ) {\displaystyle {\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})} ,

donde es la densidad de corriente y es la densidad de carga superficial . [1] Yo {\estilo de visualización J} σ {\estilo de visualización \sigma}

Xmon

El diseño del Xmon es muy similar al de un transmon, ya que se originó a partir del modelo transmon planar. [33] Un Xmon es esencialmente un transmon ajustable. La principal diferencia distintiva entre los cúbits transmon y Xmon es que los primeros están conectados a tierra con uno de sus capacitores. [34]

Gatemon

Otra variación del qubit transmon es el Gatemon. Al igual que el Xmon, el Gatemon es una variación ajustable del transmon. El Gatemon se puede ajustar a través del voltaje de compuerta .

Circuito superconductor formado por 3 Unimons (azules), cada uno conectado a resonadores (rojos), líneas de accionamiento (verdes) y líneas de sonda conjuntas (amarillas) [35]

Unimon

En 2022, investigadores de IQM Quantum Computers, la Universidad Aalto y el Centro de Investigación Técnica VTT de Finlandia descubrieron un nuevo qubit superconductor conocido como Unimon. [36] Un qubit relativamente simple, el Unimon consiste en una única unión Josephson derivada por un inductor lineal (que posee una inductancia que no depende de la corriente) dentro de un resonador (superconductor) . [37] Los Unimons tienen una anarmocidad aumentada y muestran un tiempo de operación más rápido, lo que resulta en una menor susceptibilidad a errores de ruido. [37] Además de una mayor anarmocidad, otras ventajas del qubit Unimon incluyen una menor susceptibilidad al ruido de flujo y una insensibilidad total al ruido de carga de CC. [22]

Arquetipos de cúbits superconductores [38]
Tipo
Aspecto
Carga de qubitQubit RF-SQUID (prototipo del Flux Qubit)Cubit de fase
Circuito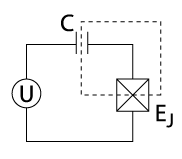
Circuito de cúbits de carga. Se define una isla superconductora (rodeada con una línea discontinua) entre los conductores de un condensador con capacidad y una unión Josephson con energía polarizada por voltaje . do {\estilo de visualización C} mi Yo Estilo de visualización E_ {J}} tú {\estilo de visualización U}
Circuito de cúbits de flujo. Un bucle superconductor con inductancia se interrumpe por una unión con energía de Josephson . El flujo de polarización se induce mediante una línea de flujo con corriente . yo {\estilo de visualización L} mi Yo Estilo de visualización E_ {J}} Φ {\estilo de visualización \Phi} I 0 {\displaystyle I_{0}}
Circuito qubit de fase. Una unión Josephson con parámetro de energía está polarizada por la corriente . mi Yo Estilo de visualización E_ {J}} I 0 {\displaystyle I_{0}}
Hamiltoniano

yo = mi do ( norte − norte gramo ) 2 − mi Yo porque ⁡ ϕ {\displaystyle H=E_{C}(N-N_{g})^{2}-E_{J}\cos \phi }

En este caso, es el número de pares de Cooper que se tunelizan a través de la unión, es la carga del capacitor en unidades de número de pares de Cooper, es la energía de carga asociada tanto con la capacitancia como con la capacitancia de la unión Josephson . norte {\estilo de visualización N} norte gramo = do V 0 / 2 mi {\displaystyle N_{g}=CV_{0}/2e} mi do = ( 2 mi ) 2 / 2 ( do Yo + do ) {\displaystyle E_{C}=(2e)^{2}/2(C_{J}+C)} do {\estilo de visualización C} do Yo Estilo de visualización C_ {J}}

yo = q 2 2 do Yo + ( Φ 0 2 π ) 2 ϕ 2 2 yo − mi Yo porque ⁡ [ ϕ − Φ 2 π Φ 0 ] {\displaystyle H={\frac {q^{2}}{2C_{J}}}+\left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]}

Téngase en cuenta que solo se permite tomar valores mayores que y se define alternativamente como la integral temporal del voltaje a lo largo de la inductancia . ϕ {\displaystyle \phi } 2 π {\displaystyle 2\pi } L {\displaystyle L}

H = ( 2 e ) 2 2 C J q 2 − I 0 Φ 0 2 π ϕ − E J cos ⁡ ϕ {\displaystyle H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi } Aquí está el flujo magnético cuántico. Φ 0 {\displaystyle \Phi _{0}}

Potencial
U = − E J cos ⁡ ϕ {\displaystyle U=-E_{J}\cos \phi } . La tensión de polarización se establece de forma que , minimizando la brecha de energía entre y , distinguiendo en consecuencia la brecha de otras brechas de energía (por ejemplo, la brecha entre y ). La diferencia en las brechas permite abordar transiciones de a y viceversa únicamente, sin completar otros estados. N g = 1 2 {\displaystyle N_{g}={\frac {1}{2}}} | 0 ⟩ {\displaystyle |0\rangle } | 1 ⟩ {\displaystyle |1\rangle } | 1 ⟩ {\displaystyle |1\rangle } | 2 ⟩ {\displaystyle |2\rangle } | 0 ⟩ {\displaystyle |0\rangle } | 1 ⟩ {\displaystyle |1\rangle }
U = ( Φ 0 2 π ) 2 ϕ 2 2 L − E J cos ⁡ [ ϕ − Φ 2 π Φ 0 ] {\displaystyle U=\left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]} El flujo de polarización es . Los diferentes pozos corresponden a un número distinto de cuantos de flujo atrapados en los bucles superconductores. Los dos estados inferiores corresponden a una superposición simétrica y antisimétrica de cuantos de flujo atrapados cero o únicos, a veces denominados estados de corriente de bucle en sentido horario y antihorario: y . Φ = Φ 0 / 2 {\displaystyle \Phi =\Phi _{0}/2} | 0 ⟩ = [ | ↺ ⟩ + | ↻ ⟩ ] / 2 {\displaystyle |0\rangle =\left[|\circlearrowleft \rangle +|\circlearrowright \rangle \right]/{\sqrt {2}}} | 1 ⟩ = [ | ↺ ⟩ − | ↻ ⟩ ] / 2 {\displaystyle |1\rangle =\left[|\circlearrowleft \rangle -|\circlearrowright \rangle \right]/{\sqrt {2}}}
U = − I 0 Φ 0 2 π ϕ − E J cos ⁡ ϕ {\displaystyle U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi } , también conocido como potencial 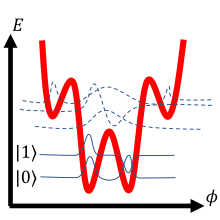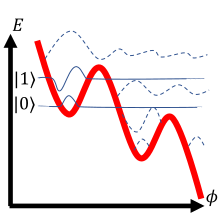de "tabla de lavar". La corriente de polarización se ajusta para permitir pozos lo suficientemente poco profundos como para contener exactamente dos funciones de onda localizadas. Un ligero aumento en la corriente de polarización provoca un "derrame" selectivo de un estado de mayor energía ( ), expresado con un pico de voltaje medible (un mecanismo comúnmente utilizado para la medición de cúbits de fase ). | 1 ⟩ {\displaystyle |1\rangle }

En la tabla anterior se analizan los tres arquetipos de cúbits superconductores. En la primera fila se presenta el diagrama del circuito eléctrico del cúbit. La segunda fila representa un hamiltoniano cuántico derivado del circuito. En general, el hamiltoniano es la suma de los componentes de energía cinética y potencial del sistema (análogo a una partícula en un pozo de potencial ). Para los hamiltonianos denotados, es la diferencia de fase de la función de onda superconductora a través de la unión, es la capacitancia asociada con la unión Josephson y es la carga en la capacitancia de la unión. Para cada potencial representado, solo se utilizan funciones de onda sólidas para el cálculo. El potencial del cúbit se indica con una línea roja gruesa y las soluciones esquemáticas de la función de onda se representan con líneas delgadas, elevadas a su nivel de energía apropiado para mayor claridad. ϕ {\displaystyle \phi } C J {\displaystyle C_{J}} q {\displaystyle q}

Obsérvese que la masa de la partícula corresponde a una función inversa de la capacitancia del circuito y que la forma del potencial está determinada por inductores regulares y uniones Josephson. Las soluciones de onda esquemáticas en la tercera fila de la tabla muestran la amplitud compleja de la variable de fase. Específicamente, si se mide la fase de un cúbit mientras el cúbit ocupa un estado particular, existe una probabilidad distinta de cero de medir un valor específico solo donde la función de onda representada oscila. Las tres filas son esencialmente presentaciones diferentes del mismo sistema físico.

cúbits individuales

La brecha de energía de GHz entre los niveles de energía de un qubit superconductor está diseñada para ser compatible con el equipo electrónico disponible, debido a la brecha de terahercios (falta de equipo en la banda de frecuencia más alta ). La brecha de energía del superconductor implica un límite superior de operación por debajo de ~1 THz más allá del cual se rompen los pares de Cooper, por lo que la separación de niveles de energía no puede ser demasiado alta. Por otro lado, la separación de niveles de energía no puede ser demasiado pequeña debido a consideraciones de enfriamiento: una temperatura de 1 K implica fluctuaciones de energía de 20 GHz. Se logran temperaturas de decenas de milikelvins en refrigeradores de dilución y permiten la operación de qubit a una separación de niveles de energía de ~5 GHz. La separación de niveles de energía de qubit se ajusta con frecuencia controlando una línea de corriente de polarización dedicada , proporcionando una "perilla" para ajustar con precisión los parámetros del qubit.

Puertas de un solo qubit

Una representación de la esfera de Bloch

Una puerta de un solo cúbit se logra mediante la rotación en la esfera de Bloch . Las rotaciones entre diferentes niveles de energía de un solo cúbit se inducen mediante pulsos de microondas enviados a una antena o línea de transmisión acoplada al cúbit con una frecuencia resonante con la separación de energía entre niveles. Los cúbits individuales pueden ser direccionados por una línea de transmisión dedicada o por una compartida si los otros cúbits están fuera de resonancia . El eje de rotación se establece mediante la modulación de amplitud en cuadratura del pulso de microondas, mientras que la longitud del pulso determina el ángulo de rotación . [39]

De manera más formal (siguiendo la notación de [39] ) para una señal de conducción

E ( t ) = E x ( t ) cos ⁡ ( ω d t ) + E y ( t ) sin ⁡ ( ω d t ) {\displaystyle {\mathcal {E}}(t)={\mathcal {E}}^{x}(t)\cos(\omega _{d}t)+{\mathcal {E}}^{y}(t)\sin(\omega _{d}t)}

de frecuencia , un hamiltoniano de qubit impulsado en una aproximación de onda rotatoria es ω d {\displaystyle \omega _{d}}

H R / ℏ = ( ω − ω d ) | 1 ⟩ ⟨ 1 | + E x ( t ) 2 σ x + E y ( t ) 2 σ y {\displaystyle H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}} ,

donde es la resonancia del qubit y son matrices de Pauli . ω {\displaystyle \omega } σ x , σ y {\displaystyle \sigma _{x},\sigma _{y}}

Para implementar una rotación sobre el eje, se puede configurar y aplicar un pulso de microondas a una frecuencia durante un tiempo . La transformación resultante es X {\displaystyle X} E y ( t ) = 0 {\displaystyle {\mathcal {E}}^{y}(t)=0} ω d = ω {\displaystyle \omega _{d}=\omega } t g {\displaystyle t_{g}}

U x = exp ⁡ { − i ℏ ∫ 0 t g H R d t } = exp ⁡ { − i ∫ 0 t g E x ( t ) d t ⋅ σ x / 2 } {\displaystyle U_{x}=\exp \left\{-{\frac {i}{\hbar }}\int _{0}^{t_{g}}H^{R}dt\right\}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}} .

Este es exactamente el operador de rotación por ángulo sobre el eje en la esfera de Bloch. Una rotación sobre el eje se puede implementar de manera similar. Mostrar los dos operadores de rotación es suficiente para satisfacer la universalidad , ya que cada operador unitario de cúbit puede presentarse como (hasta una fase global que es físicamente intrascendente) mediante un procedimiento conocido como descomposición. [40] La configuración da como resultado la transformación R X ( θ ) {\displaystyle R_{X}(\theta )} θ = ∫ 0 t g E x ( t ) d t {\displaystyle \theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt} X {\displaystyle X} Y {\displaystyle Y} U {\displaystyle U} U = R X ( θ 1 ) R Y ( θ 2 ) R X ( θ 3 ) {\displaystyle U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})} X − Y {\displaystyle X-Y} ∫ 0 t g E x ( t ) d t = π {\displaystyle \int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi }

U x = exp ⁡ { − i ∫ 0 t g E x ( t ) d t ⋅ σ x / 2 } = e − i π σ x / 2 = − i σ x {\displaystyle U_{x}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}=e^{-i\pi \sigma _{x}/2}=-i\sigma _{x}}

hasta la fase global y se conoce como puerta NOT . − i {\displaystyle -i}

Acoplamiento de qubits

La capacidad de acoplar qubits es esencial para implementar puertas de 2 qubits . El acoplamiento de dos qubits se puede lograr conectando ambos a un circuito de acoplamiento eléctrico intermedio. El circuito puede ser un elemento fijo (como un condensador) o ser controlable (como el DC-SQUID ). En el primer caso, el desacoplamiento de los qubits durante el tiempo en que la puerta está apagada se logra al sintonizar los qubits fuera de resonancia entre sí, lo que hace que las brechas de energía entre sus estados computacionales sean diferentes. [41] Este enfoque está inherentemente limitado al acoplamiento del vecino más cercano, ya que se debe diseñar un circuito eléctrico físico entre los qubits conectados. En particular, el acoplamiento del vecino más cercano de D-Wave Systems logra una celda unitaria altamente conectada de 8 qubits en la configuración del gráfico Chimera. Los algoritmos cuánticos generalmente requieren el acoplamiento entre qubits arbitrarios. En consecuencia, son necesarias múltiples operaciones de intercambio , lo que limita la longitud del cálculo cuántico posible antes de la decoherencia del procesador .

Bus cuántico

Otro método para acoplar dos o más qubits es por medio de un bus cuántico , emparejando qubits con este intermedio. Un bus cuántico se implementa a menudo como una cavidad de microondas modelada por un oscilador armónico cuántico. Los qubits acoplados pueden entrar y salir de la resonancia con el bus y entre sí, eliminando la limitación del vecino más cercano. El formalismo que describe el acoplamiento es la electrodinámica cuántica de cavidades . En la electrodinámica cuántica de cavidades, los qubits son análogos a los átomos que interactúan con una cavidad de fotones ópticos con una diferencia de GHz (en lugar del régimen de THz de radiación electromagnética). El intercambio de excitación resonante entre estos átomos artificiales es potencialmente útil para la implementación directa de puertas multi-qubit. [42] Siguiendo la variedad de estados oscuros , el esquema de Khazali-Mølmer [42] realiza operaciones complejas multi-qubit en un solo paso, proporcionando un atajo sustancial al modelo de circuito convencional.

Puerta resonante cruzada

Un mecanismo de compuerta popular utiliza dos cúbits y un bus, cada uno ajustado a diferentes separaciones de niveles de energía. La aplicación de excitación de microondas al primer cúbit, con una frecuencia resonante con el segundo cúbit, provoca una rotación del segundo cúbit. La dirección de rotación depende del estado del primer cúbit, lo que permite una construcción de compuerta de fase controlada . [43] σ x {\displaystyle \sigma _{x}}

Siguiendo la notación de, [43] el hamiltoniano impulsor que describe el sistema excitado a través de la primera línea impulsora del qubit se escribe formalmente

H D / ℏ = A ( t ) cos ⁡ ( ω ~ 2 t ) ( σ x ⊗ I − J Δ 12 σ z ⊗ σ x + m 12 I ⊗ σ x ) {\displaystyle H_{D}/\hbar =A(t)\cos({\tilde {\omega }}_{2}t)\left(\sigma _{x}\otimes I-{\frac {J}{\Delta _{12}}}\sigma _{z}\otimes \sigma _{x}+m_{12}I\otimes \sigma _{x}\right)} ,

donde es la forma del pulso de microondas en el tiempo, es la frecuencia de resonancia del segundo qubit, son las matrices de Pauli , es el coeficiente de acoplamiento entre los dos qubits a través del resonador, es la desintonización del qubit, es el acoplamiento disperso (no deseado) entre qubits, y es la constante de Planck reducida . La integral temporal sobre determina el ángulo de rotación. Las rotaciones no deseadas de los términos primero y tercero del hamiltoniano se pueden compensar con operaciones de un solo qubit. El componente restante, combinado con rotaciones de un solo qubit, forma una base para el álgebra de Lie su(4) . A ( t ) {\displaystyle A(t)} ω ~ 2 {\displaystyle {\tilde {\omega }}_{2}} { I , σ x , σ y , σ z } {\displaystyle \{I,\sigma _{x},\sigma _{y},\sigma _{z}\}} J {\displaystyle J} Δ 12 ≡ ω 1 − ω 2 {\displaystyle \Delta _{12}\equiv \omega _{1}-\omega _{2}} m 12 {\displaystyle m_{12}} ℏ {\displaystyle \hbar } A ( t ) {\displaystyle A(t)}

Puerta de fase geométrica

Se pueden utilizar niveles superiores (fuera del subespacio computacional) de un par de circuitos superconductores acoplados para inducir una fase geométrica en uno de los estados computacionales de los qubits. Esto conduce a un cambio de fase condicional de entrelazamiento de los estados relevantes de los qubits. Este efecto se ha implementado mediante el ajuste de flujo de los espectros de los qubits [44] y mediante el uso de excitación selectiva por microondas. [45] La excitación fuera de resonancia se puede utilizar para inducir un cambio diferencial de ac-Stark, lo que permite la implementación de puertas de fase controladas completamente por microondas. [46]

Interacciones de Heisenberg

El modelo de interacciones de Heisenberg, escrito como

H ^ X X Z / ℏ = ∑ i , j J X Y ( σ ^ x i σ ^ x j + σ ^ y i σ ^ y j ) + J Z Z σ ^ z i σ ^ z j {\displaystyle {\hat {\mathcal {H}}}_{\mathrm {XXZ} }/\hbar =\sum _{i,j}J_{\mathrm {XY} }({\hat {\sigma }}_{\text{x}}^{i}{\hat {\sigma }}_{\text{x}}^{j}+{\hat {\sigma }}_{\text{y}}^{i}{\hat {\sigma }}_{\text{y}}^{j})+J_{\mathrm {ZZ} }{\hat {\sigma }}_{\text{z}}^{i}{\hat {\sigma }}_{\text{z}}^{j}} ,

sirve como base para la simulación cuántica analógica de sistemas de espín y como primitiva para un conjunto expresivo de puertas cuánticas, a veces denominadas puertas de simulación fermiónica (o fSim ). En circuitos superconductores, este modelo de interacción se ha implementado utilizando qubits ajustables por flujo con acoplamiento ajustable por flujo, [47] lo que permite la demostración de la supremacía cuántica. [48] Además, también se puede realizar en qubits de frecuencia fija con acoplamiento fijo utilizando controladores de microondas. [49] La familia de puertas fSim abarca unidades arbitrarias de dos qubits XY y ZZ, incluidas las puertas iSWAP, CZ y SWAP (consulte Puerta lógica cuántica ).

Lectura de qubit

Existen mecanismos de lectura o medición específicos de la arquitectura . La lectura de un qubit de fase se explica en la tabla de arquetipos de qubit anterior. Un estado de qubit de flujo a menudo se lee utilizando un magnetómetro DC- SQUID ajustable . Los estados también se pueden medir utilizando un electrómetro . [1] Un esquema de lectura más general incluye un acoplamiento a un resonador de microondas , donde la frecuencia de resonancia del resonador se desplaza de forma dispersiva por el estado del qubit. [50] [51] Los sistemas multinivel (qudits) se pueden leer utilizando estanterías de electrones. [52]

Criterios de DiVincenzo

Los criterios de DiVincenzo son una lista que describe los requisitos para que un sistema físico sea capaz de implementar un cúbit lógico. Los criterios de DiVincenzo se satisfacen mediante la implementación de computación cuántica superconductora. Gran parte del esfuerzo de desarrollo actual en computación cuántica superconductora apunta a lograr interconexión, control y lectura en la tercera dimensión con capas de litografía adicionales . La lista de criterios de DiVincenzo para que un sistema físico implemente un cúbit lógico se satisface mediante la implementación de cúbits superconductores. Aunque los criterios de DiVincenzo tal como se propusieron originalmente consisten en cinco criterios necesarios para implementar físicamente una computadora cuántica, la lista más completa consta de siete criterios, ya que tiene en cuenta la comunicación a través de una red de computadoras capaz de transmitir información cuántica entre computadoras, conocida como la "internet cuántica". Por lo tanto, los primeros cinco criterios garantizan una computación cuántica exitosa, mientras que los dos criterios finales permiten la comunicación cuántica.

  1. Un sistema físico escalable con qubits bien caracterizados. "Bien caracterizado implica que esa función hamiltoniana debe estar bien definida, es decir, los estados propios de energía del qubit deben poder cuantificarse. Un sistema escalable se explica por sí solo, indica que esta capacidad de regular un qubit debe ser ampliable para muchos más qubits. Aquí radica el principal problema al que se enfrentan las computadoras cuánticas, ya que a medida que se implementan más qubits, conduce a un aumento exponencial en el costo y otras implementaciones físicas que palidecen en comparación con la velocidad mejorada que puede ofrecer. [11] Como los qubits superconductores se fabrican en un chip, el sistema de muchos qubits es fácilmente escalable. Los qubits se asignan en la superficie 2D del chip. La demanda de qubits bien caracterizados se satisface con (a) no linealidad de qubit (acceso solo a dos de los niveles de energía disponibles) y (b) acceso a un solo qubit a la vez (en lugar de todo el sistema de muchos qubits) mediante líneas de control dedicadas por qubit y/o separación de frecuencia, o ajuste fuera, de diferentes qubits.
  2. Capacidad de inicializar el estado de los cúbits a un estado fiducial simple. [53] Un estado fiducial es uno que se puede replicar de manera fácil y consistente y es útil en computación cuántica, ya que se puede utilizar para garantizar el estado inicial de los cúbits. Una forma sencilla de inicializar un cúbit superconductor es esperar el tiempo suficiente para que los cúbits se relajen al estado fundamental. Controlar el potencial de los cúbits con perillas de ajuste permite mecanismos de inicialización más rápidos.
  3. Tiempos de decoherencia relevantes largos [53] . La decoherencia de los qubits superconductores se ve afectada por múltiples factores. La mayor parte de la decoherencia se atribuye a la calidad de la unión Josephson y a las imperfecciones en el sustrato del chip. Debido a su escala mesoscópica, los qubits superconductores tienen una vida útil relativamente corta. Sin embargo, se han demostrado miles de operaciones de compuerta en estos sistemas de muchos qubits. [54] Las estrategias recientes para mejorar la coherencia del dispositivo incluyen la purificación de los materiales del circuito y el diseño de qubits con una menor sensibilidad a las fuentes de ruido. [24]
  4. Un conjunto "universal" de puertas cuánticas. [53] Los qubits superconductores permiten rotaciones arbitrarias en la esfera de Bloch con señales de microondas pulsadas, implementando puertas de un solo qubit. y se muestran acoplamientos para la mayoría de las implementaciones y para complementar el conjunto de puertas universales. [55] [56] [49] Este criterio también puede satisfacerse acoplando dos transmonedas con un condensador de acoplamiento. [1] σ z σ z {\displaystyle \sigma _{z}\sigma _{z}} σ x σ x {\displaystyle \sigma _{x}\sigma _{x}}
  5. Capacidad de medición específica de qubits. [53] En general, se utilizan qubits superconductores individuales para control o medición.
  6. Interconvertibilidad de qubits estacionarios y volantes. [53] Mientras que los qubits estacionarios se utilizan para almacenar información o realizar cálculos, los qubits volantes transmiten información macroscópicamente. Los qubits deberían ser capaces de convertirse de qubits estacionarios a volantes y viceversa.
  7. Transmisión confiable de qubits voladores entre ubicaciones específicas. [53]

Los dos últimos criterios han sido probados experimentalmente mediante una investigación realizada por ETH con dos qubits superconductores conectados por un cable coaxial . [57]

Desafíos

Uno de los principales desafíos de la computación cuántica superconductora son las temperaturas extremadamente bajas a las que existen los superconductores como los condensados ​​de Bose-Einstein. Otros desafíos básicos en el diseño de qubits superconductores son la configuración del pozo de potencial y la elección de la masa de las partículas de manera que la separación de energía entre dos niveles de energía específicos sea única, diferente de todas las demás separaciones de energía entre niveles en el sistema, ya que estos dos niveles se utilizan como estados lógicos del qubit.

La computación cuántica superconductora también debe mitigar el ruido cuántico (las interrupciones del sistema causadas por su interacción con un entorno) así como las fugas (la información que se pierde en el entorno circundante). Una forma de reducir las fugas es con mediciones de paridad . [16] Otra estrategia es utilizar qubits con gran anarmonicidad. [26] [27] Muchos de los desafíos actuales a los que se enfrenta la computación cuántica superconductora se encuentran en el campo de la ingeniería de microondas. [50] A medida que la computación cuántica superconductora se acerca a dispositivos de mayor escala, los investigadores se enfrentan a dificultades en la coherencia de qubits , el software de calibración escalable , la determinación eficiente de la fidelidad de los estados cuánticos en todo un chip y la fidelidad de qubits y compuertas. [16] Además, los dispositivos de computación cuántica superconductora deben ser reproducibles de forma fiable a escalas cada vez mayores de modo que sean compatibles con estas mejoras. [16]

El viaje de la computación cuántica superconductora:

Aunque no es el desarrollo más reciente, el foco comenzó a desplazarse hacia los qubits superconductores en la segunda mitad de la década de 1990, cuando se hizo evidente la tunelización cuántica a través de las uniones Josephson, lo que permitió comprender que la computación cuántica podía lograrse a través de estos qubits superconductores. [58]

A finales de siglo, en 1999, Yasunobu Nakamura publicó un artículo [59] que mostraba el diseño inicial de un cúbit superconductor que ahora se conoce como "cúbit de carga". Este es el punto de partida principal sobre el que se modificaron los diseños posteriores. Estos cúbits iniciales tenían sus limitaciones con respecto al mantenimiento de tiempos de coherencia largos y mediciones destructivas. La modificación posterior de este avance inicial condujo a la invención del cúbit de fase y flujo y, posteriormente, al cúbit transmon, que ahora se usa ampliamente y principalmente en la computación cuántica superconductora. El cúbit transmon ha mejorado los diseños originales y ha amortiguado aún más el ruido de carga del cúbit. [58]

El viaje ha sido largo, arduo y lleno de avances, pero ha visto avances significativos en la historia reciente y tiene un potencial enorme para revolucionar la informática.

El futuro de la computación cuántica superconductora:

Los principales gigantes industriales del sector, como Google, IBM y Baidu, están utilizando la computación cuántica superconductora y los qubits transmon para dar pasos agigantados en el área de la computación cuántica.

En agosto de 2022, Baidu dio a conocer sus planes para construir una computadora cuántica totalmente integrada de arriba a abajo que incorporará cúbits superconductores. Esta computadora será integral, con hardware, software y aplicaciones totalmente integrados. Se trata de una primicia en el mundo de la computación cuántica y conducirá a avances revolucionarios. [60]

IBM publicó la siguiente hoja de ruta que ha establecido para sus computadoras cuánticas que también incorporan qubits superconductores y el qubit transmon.

2021: En 2021, IBM lanzó su procesador de 127 qubits. [61]
2022: El 9 de noviembre, IBM anunció su procesador de 433 qubits llamado "Osprey". [62]
2023: IBM planea lanzar su procesador cuántico Condor con 1.121 qubits. [61]
2024: IBM planea lanzar su procesador cuántico Flamingo con más de 1386 qubits. [61]
2025: IBM planea lanzar su procesador cuántico Kookaburra con más de 4158 qubits. [61]
2026 y más allá: IBM planea lanzar un procesador cuántico que pueda escalar más allá de los 10 000 qubits hasta los 100 000 qubits. [61]

En 2016, Google implementó 16 qubits para transmitir una demostración del modelo de Fermi-Hubbard . En otro experimento reciente, Google utilizó 17 qubits para optimizar el modelo de Sherrington-Kirkpatrick . Google produjo la computadora cuántica Sycamore, que realizó una tarea en 200 segundos que habría llevado 10.000 años en una computadora clásica. [63]

Referencias

  1. ^ abcdef "Documentación de PennyLane — PennyLane". docs.pennylane.ai . Consultado el 11 de diciembre de 2022 .
  2. ^ Castelvecchi, Davide (5 de enero de 2017). «Los ordenadores cuánticos listos para saltar del laboratorio en 2017». Nature . 541 (7635): 9–10. Bibcode :2017Natur.541....9C. doi : 10.1038/541009a . PMID  28054624. S2CID  4447373.
  3. ^ ab "IBM pone a disposición computación cuántica en IBM Cloud". www-03.ibm.com . 4 de mayo de 2016. Archivado desde el original el 4 de mayo de 2016.
  4. ^ "Imec entra en la carrera para liberar la computación cuántica con qubits de silicio". www.imec-int.com . Consultado el 10 de noviembre de 2019 .
  5. ^ Colm A. Ryan, Blake R. Johnson, Diego Ristè, Brian Donovan, Thomas A. Ohki, "Hardware para computación cuántica dinámica", arXiv:1704.08314v1
  6. ^ "Rigetti lanza servicios de nube cuántica y anuncia un desafío de un millón de dólares". HPCwire . 2018-09-07 . Consultado el 2018-09-16 .
  7. ^ "Intel invierte 50 millones de dólares para impulsar la computación cuántica | Intel Newsroom". Intel Newsroom .
  8. ^ Kelly, J.; Barends, R.; Fowler, AG; Megrant, A.; Jeffrey, E.; White, TC; Sank, D.; Mutus, JY; Campbell, B.; Chen, Yu; Chen, Z.; Chiaro, B.; Dunsworth, A.; Hoi, I.-C.; Neill, C.; O'Malley, PJJ; Quintana, C.; Roushan, P.; Vainsencher, A.; Wenner, J.; Cleland, AN; Martinis, John M. (4 de marzo de 2015). "Preservación del estado mediante detección de errores repetitivos en un circuito cuántico superconductor". Nature . 519 (7541): 66–69. arXiv : 1411.7403 . Código Bibliográfico :2015Natur.519...66K. doi :10.1038/nature14270. Número de modelo: PMID  25739628. Número de modelo: S2CID  3032369.
  9. ^ Arute, Frank; Arya, Kunal; Babbush, Ryan; Tocino, Dave; Bardin, José C.; Barends, Rami; Biswas, Rupak; Boixó, Sergio; Brandao, Fernando GSL; Buell, David A.; Burkett, Brian; Chen, Yu; Chen, Zijun; Claro, Ben; Collins, Roberto; Courtney, William; Dunsworth, Andrés; Farhi, Eduardo; Foxen, Brooks; Cazador de aves, Austin; Gidney, Craig; Justina, Marissa; Graff, Rob; Guérin, Keith; Habegger, Steve; Harrigan, Mateo P.; Hartmann, Michael J.; Hola, Alan; Hoffmann, Markus; Huang, Trento; Humilde, Travis S.; Isakov, Sergei V.; Jeffrey, Evan; Jiang, Zhang; Kafri, Dvir; Kechedzhi, Kostyantyn; Kelly, Julián; Klimov, Paul V.; Knysh, Sergey; Korotkov, Alejandro; Kostritsa, Fedor; Landhuis, David; Lindmark, Mike; Lucero, Erik; Lyakh, Dmitry; Mandrá, Salvatore; McClean, Jarrod R.; McEwen, Mateo; Megan, Antonio; Mi, Xiao; Michielsen, Kristel; Mohseni, Masoud; Mutus, Josh; Naamán, Ofer; Neeley, Mateo; Neill, Carlos; Niu, Murphy Yuezhen; Ostby, Eric; Petukhov, André; Platt, John C.; Quintana, Chris; Rieffel, Eleanor G.; Roushan, Pedram; Rubin, Nicolás C.; Se hundió, Daniel; Satzinger, Kevin J.; Smelyanskiy, Vadim; Sung, Kevin J.; Trevithick, Mateo D.; Vainsencher, Amit; Villalonga, Benjamín; Blanco, Teodoro; Yao, Z. Jamie; Sí, Ping; Zalcman, Adán; Neven, Hartmut; Martinis, John M. (octubre de 2019). "Supremacía cuántica utilizando un procesador superconductor programable". Nature . 574 (7779): 505–510. arXiv : 1910.11333 . Bibcode :2019Natur.574..505A. doi : 10.1038/s41586-019-1666-5 . Número de identificación personal  31645734.
  10. ^ Dayal, Geeta. "La máquina de Turing de LEGO es sencilla, pero sublime". WIRED .
  11. ^ ab "Criterios de DiVincenzo – Códice de computación cuántica". qc-at-davis.github.io . Consultado el 13 de diciembre de 2022 .
  12. ^ ab Ballon, Alvaro (22 de marzo de 2022). "Computación cuántica con cúbits superconductores — PennyLane". Demostraciones de Pennylane . Consultado el 13 de diciembre de 2022 .
  13. ^ "Pares de Cooper".
  14. ^ Shen, LYL (1972-02-01). "Superconductividad del tantalio, niobio y lantano estudiada mediante efecto túnel de electrones: problemas de contaminación superficial". Actas de la conferencia AIP . 4 (1): 31–44. Bibcode :1972AIPC....4...31S. doi :10.1063/1.2946195. ISSN  0094-243X.
  15. ^ Greicius, Tony (12 de junio de 2020). «El laboratorio de átomos fríos de la NASA da un gran paso hacia la ciencia cuántica». NASA . Consultado el 11 de diciembre de 2022 .
  16. ^ abcde Kjaergaard, Morten; Schwartz, Mollie E.; Braumüller, Jochen; Krantz, Philip; Wang, Joel I.-Jan; Gustavsson, Simon; Oliver, William D. (10 de marzo de 2020). "Cubits superconductores: estado actual de la cuestión". Revisión anual de física de la materia condensada . 11 (1): 369–395. arXiv : 1905.13641 . Código Bibliográfico :2020ARCMP..11..369K. doi :10.1146/annurev-conmatphys-031119-050605. ISSN  1947-5454. S2CID  173188891.
  17. ^ Manucharyan, VE; Koch, J.; Glazman, LI; Devoret, MH (1 de octubre de 2009). "Fluxonio: circuitos de pares de Cooper individuales sin carga". Science . 326 (5949): 113–116. arXiv : 0906.0831 . Bibcode :2009Sci...326..113M. doi :10.1126/science.1175552. PMID  19797655. S2CID  17645288.
  18. ^ Houck, AA; Koch, Jens; Devoret, MH; Girvin, SM; Schoelkopf, RJ (11 de febrero de 2009). "Vida después del ruido de carga: resultados recientes con qubits transmon". Procesamiento de información cuántica . 8 (2–3): 105–115. arXiv : 0812.1865 . doi :10.1007/s11128-009-0100-6. S2CID  27305073.
  19. ^ Barends, R.; Kelly, J.; Megrant, A.; Sank, D.; Jeffrey, E.; Chen, Y.; Yin, Y.; Chiaro, B.; Mutus, J.; Neill, C.; O'Malley, P.; Roushan, P.; Wenner, J.; White, TC; Cleland, AN; Martinis, John M. (22 de agosto de 2013). "Un qubit Josephson coherente adecuado para circuitos integrados cuánticos escalables". Physical Review Letters . 111 (8): 080502. arXiv : 1304.2322 . Código Bibliográfico :2013PhRvL.111h0502B. doi :10.1103/PhysRevLett.111.080502. Número de modelo  : PMID24010421 . Número de modelo: S2CID27081288  .
  20. ^ Metcalfe, M.; Boaknin, E.; Manucharyan, V.; Vijay, R.; Siddiqi, I.; Rigetti, C.; Frunzio, L.; Schoelkopf, RJ; Devoret, MH (21 de noviembre de 2007). "Medición de la decoherencia de un qubit de quantronio con el amplificador de bifurcación de cavidad". Physical Review B . 76 (17): 174516. arXiv : 0706.0765 . Código Bibliográfico :2007PhRvB..76q4516M. doi :10.1103/PhysRevB.76.174516. S2CID  19088840.
  21. ^ abcd Martinis, John M.; Osborne, Kevin (16 de febrero de 2004). "Cubits superconductores y la física de las uniones Josephson". arXiv : cond-mat/0402415 . Código Bibliográfico :2004cond.mat..2415M. {{cite journal}}: Requiere citar revista |journal=( ayuda )
  22. ^ abc Hyyppä, Eric; Kundu, Suman; Chan, Chun Fai; Gunyhó, András; Hotari, Juho; Janzso, David; Juliusson, Kristinn; Kiuru, Olavi; Kotilahti, Janne; Landra, Alejandro; Liu, Wei; Marxer, Fabián; Mäkinen, Akseli; Orgiazzi, Jean-Luc; Palma, Mario (12/11/2022). "Qubit Unimon". Comunicaciones de la naturaleza . 13 (1): 6895. arXiv : 2203.05896 . Código Bib : 2022NatCo..13.6895H. doi :10.1038/s41467-022-34614-w. ISSN  2041-1723. PMC 9653402 . Número de modelo:  PMID36371435. 
  23. ^ ab Cottet, Nathanaël; Xiong, Haonan; Nguyen, Long B.; Lin, Yen-Hsiang; Manucharyan, Vladimir E. (4 de noviembre de 2021). "Estanterías electrónicas de un átomo artificial superconductor". Nature Communications . 12 (1): 6383. arXiv : 2008.02423 . Código Bibliográfico :2021NatCo..12.6383C. doi :10.1038/s41467-021-26686-x. ISSN  2041-1723. PMC 8569191 . PMID  34737313. 
  24. ^ abc Nguyen, Long B.; Lin, Yen-Hsiang; Somoroff, Aarón; Mencía, Raymond; Grabón, Nicolás; Manucharyan, Vladimir E. (25 de noviembre de 2019). "Qubit de fluxonio de alta coherencia". Revisión física X. 9 (4): 041041. arXiv : 1810.11006 . Código Bib : 2019PhRvX...9d1041N. doi : 10.1103/PhysRevX.9.041041. ISSN  2160-3308. S2CID  53499609.
  25. ^ Ciencia, Universidad Nacional de; MISIS, Tecnología. "Los qubits de fluxonio acercan la creación de una computadora cuántica". phys.org . Consultado el 12 de diciembre de 2022 .
  26. ^ ab Nguyen, Long B. (2020). Hacia el procesador cuántico de fluxonio (tesis doctoral). Universidad de Maryland, College Park.
  27. ^ ab Nguyen, Long B.; Koolstra, Gerwin; Kim, Yosep; Morvan, Alexis; Chistolini, Trevor; Singh, Shraddha; Nesterov, Konstantin N.; Jünger, Christian; Chen, Larry; Pedramrazi, Zahra; Mitchell, Bradley K.; Kreikebaum, John Mark; Puri, Shruti; Santiago, David I.; Siddiqi, Irfan (5 de agosto de 2022). "Plan para un procesador cuántico de fluxonio de alto rendimiento". PRX Quantum . 3 (3): 037001. arXiv : 2201.09374 . Código Bibliográfico :2022PRXQ....3c7001N. doi : 10.1103/PRXQuantum.3.037001 .
  28. ^ "Cubits superconductores: en islas, cubits de carga y el transmon". LeftAsExercise . 2019-06-06 . Consultado el 2022-12-12 .
  29. ^ Wendin, G. (1 de octubre de 2017). "Procesamiento de información cuántica con circuitos superconductores: una revisión". Informes sobre el progreso en física . 80 (10): 106001. arXiv : 1610.02208 . Bibcode :2017RPPh...80j6001W. doi :10.1088/1361-6633/aa7e1a. ISSN  0034-4885. PMID  28682303. S2CID  3940479.
  30. ^ Gambetta, JM; Chow, JM ; Steffen, M. (2017). "Construcción de qubits lógicos en un sistema de computación cuántica superconductor". npj Quantum Information . 3 (1): 2. arXiv : 1510.04375 . Bibcode :2017npjQI...3....2G. doi : 10.1038/s41534-016-0004-0 .
  31. ^ Roth, Thomas E.; Ma, Ruichao; Chew, Weng C. (21 de junio de 2021). "Introducción al qubit transmonátil para ingenieros electromagnéticos". arXiv : 2106.11352 . {{cite journal}}: Requiere citar revista |journal=( ayuda )
  32. ^ Kjaergaard, Morten; Schwartz, Mollie E.; Braumüller, Jochen; Krantz, Philip; Wang, Joel I.-J.; Gustavsson, Simon; Oliver, William D. (10 de marzo de 2020). "Cubits superconductores: estado actual de la cuestión". Revisión anual de física de la materia condensada . 11 (1): 369–395. arXiv : 1905.13641 . Código Bibliográfico :2020ARCMP..11..369K. doi :10.1146/annurev-conmatphys-031119-050605. ISSN  1947-5454. S2CID  173188891.
  33. ^ Shim, Yun-Pil; Tahan, Charles (17 de marzo de 2016). "Principios de diseño inspirados en semiconductores para computación cuántica superconductora". Nature Communications . 7 (1): 11059. arXiv : 1507.07923 . Bibcode :2016NatCo...711059S. doi :10.1038/ncomms11059. ISSN  2041-1723. PMC 4800439 . PMID  26983379. 
  34. ^ Wang, Chenlu; Li, Xuegang; Xu, Huikai; Li, Zhiyuan; Wang, Junhua; Yang, Zhen; Mi, Zhenyu; Liang, Xuehui; Su, Tang; Yang, Chuhong; Wang, Guangyue; Wang, Wenyan; Li, Yongchao; Chen, Mo; Li, Chengyao (13 de enero de 2022). "Hacia computadoras cuánticas prácticas: qubit transmon con una vida útil cercana a los 0,5 milisegundos". npj Información cuántica . 8 (1): 3. arXiv : 2105.09890 . Código Bib : 2022npjQI...8....3W. doi :10.1038/s41534-021-00510-2. ISSN  2056-6387. S2CID  245950831.
  35. ^ "Fig. 1: qubit Unimon y su configuración de medición. | Nature Communications". {{cite journal}}: Requiere citar revista |journal=( ayuda )
  36. ^ "Unimon: Un nuevo qubit para impulsar los ordenadores cuánticos de IQM | IQM". www.meetiqm.com . Consultado el 12 de diciembre de 2022 .
  37. ^ ab Buchanan, Mark (8 de diciembre de 2022). "Conoce a Unimon, el nuevo cúbit del barrio". Física . 15 : 191. Código Bibliográfico :2022PhyOJ..15..191B. doi : 10.1103/Physics.15.191 . S2CID  257514449.
  38. ^ Devoret, MH; Wallraff, A.; Martinis, JM (6 de noviembre de 2004). "Cubits superconductores: una breve reseña". arXiv : cond-mat/0411174 .
  39. ^ ab Motzoi, F.; Gambetta, JM; Rebentrost, P.; Wilhelm, FK (8 de septiembre de 2009). "Pulsos simples para la eliminación de fugas en cúbits débilmente no lineales". Physical Review Letters . 103 (11): 110501. arXiv : 0901.0534 . Bibcode :2009PhRvL.103k0501M. doi :10.1103/PhysRevLett.103.110501. PMID  19792356. S2CID  7288207.
  40. ^ Chuang, Michael A. Nielsen e Isaac L. (2010). Computación cuántica e información cuántica (edición del décimo aniversario). Cambridge: Cambridge University Press. pp. 174–176. ISBN 978-1-107-00217-3.
  41. ^ Rigetti, Chad Tyler (2009). Puertas cuánticas para qubits superconductores . p. 21. Bibcode :2009PhDT........50R. ISBN 9781109198874.
  42. ^ ab Khazali, Mohammadsadegh; Mølmer, Klaus (11 de junio de 2020). "Puertas multiqubit rápidas por evolución adiabática en variedades de estados excitados en interacción de átomos de Rydberg y circuitos superconductores". Physical Review X . 10 (2): 021054. arXiv : 2006.07035 . Código Bibliográfico :2020PhRvX..10b1054K. doi : 10.1103/PhysRevX.10.021054 . ISSN  2160-3308.
  43. ^ ab Chow, Jerry M.; Córcoles, AD; Gambetta, Jay M.; Rigetti, Chad; Johnson, BR; Smolin, John A.; Rozen, JR; Keefe, George A.; Rothwell, Mary B.; Ketchen, Mark B.; Steffen, M. (17 de agosto de 2011). "Puerta entrelazante simple de microondas para cúbits superconductores de frecuencia fija". Physical Review Letters . 107 (8): 080502. arXiv : 1106.0553 . Código Bibliográfico :2011PhRvL.107h0502C. doi :10.1103/PhysRevLett.107.080502. PMID  21929152. S2CID  9302474.
  44. ^ DiCarlo, L.; Chow, J. M.; Gambetta, J. M.; Bishop, Lev S.; Johnson, B. R.; Schuster, DI; Majer, J.; Blais, A.; Frunzio, L.; Girvin, SM; Schoelkopf, RJ (28 de junio de 2009). "Demostración de algoritmos de dos cúbits con un procesador cuántico superconductor". Nature . 460 (7252). Springer Science and Business Media LLC: 240–244. doi :10.1038/nature08121. ISSN  0028-0836.
  45. ^ Ficheux, Quentin; Nguyen, Long B.; Somoroff, Aaron; Xiong, Haonan; Nesterov, Konstantin N.; Vavilov, Maxim G.; Manucharyan, Vladimir E. (3 de mayo de 2021). "Lógica rápida con cúbits lentos: puerta Z controlada activada por microondas en fluxonios de baja frecuencia". Physical Review X . 11 (2). arXiv : 2011.02634 . doi :10.1103/PhysRevX.11.021026. ISSN  2160-3308.
  46. ^ Xiong, Haonan; Ficheux, Quentin; Somoroff, Aaron; Nguyen, Long B.; Dogan, Ebru; Rosenstock, Dario; Wang, Chen; Nesterov, Konstantin N.; Vavilov, Maxim G.; Manucharyan, Vladimir E. (15 de abril de 2022). "Puerta de fase controlada arbitraria en cúbits de fluxonio utilizando desplazamientos de Stark de CA diferenciales". Physical Review Research . 4 (2). arXiv : 2103.04491 . doi :10.1103/PhysRevResearch.4.023040. ISSN  2643-1564.
  47. ^ Foxen, B.; Neill, C.; Dunsworth, A.; Roushan, P.; Claro, B.; Megrant, A.; Kelly, J.; Chen, Zijun; Satzinger, K.; Barends, R.; Arute, F.; Arya, K.; Babbush, R.; Tocino, D.; Bardin, JC; Boixo, S.; Buell, D.; Burkett, B.; Chen, Yu; Collins, R.; Farhi, E.; Fowler, A.; Gidney, C.; Justina, M.; Graff, R.; Harrigan, M.; Huang, T.; Isakov, SV; Jeffrey, E.; Jiang, Z.; Kafri, D.; Kechedzhi, K.; Klímov, P.; Korotkov, A.; Kostritsa, F.; Landhuis, D.; Lucero, E.; McClean, J.; McEwen, M.; Mi, X.; Mohseni, M.; Mutus, J. Y.; Naaman, O.; Neeley, M.; Niu, M.; Petukhov, A.; Quintana, C.; Rubin , N.; Sank, D.; Smelyanskiy, V.; Vainsencher, A.; White, T. C.; Yao, Z.; Yeh, P.; Zalcman, A.; Neven, H.; Martinis, J. M.; Google AI Quantum (15 de septiembre de 2020). "Demostración de un conjunto continuo de puertas de dos cúbits para algoritmos cuánticos de corto plazo". Physical Review Letters . 125 (12). arXiv : 2001.08343 . doi :10.1103/PhysRevLett.125.120504. Revista de Ciencias Sociales y Humanidades (Revista  de Ciencias Sociales y Humanidades). {{cite journal}}: |author58=tiene nombre genérico ( ayuda )
  48. ^ Arute, Frank; Arya, Kunal; Babbush, Ryan; Tocino, Dave; Bardin, José C.; Barends, Rami; Biswas, Rupak; Boixó, Sergio; Brandao, Fernando GSL; Buell, David A.; Burkett, Brian; Chen, Yu; Chen, Zijun; Claro, Ben; Collins, Roberto; Courtney, William; Dunsworth, Andrés; Farhi, Eduardo; Foxen, Brooks; Cazador de aves, Austin; Gidney, Craig; Justina, Marissa; Graff, Rob; Guérin, Keith; Habegger, Steve; Harrigan, Mateo P.; Hartmann, Michael J.; Hola, Alan; Hoffmann, Markus; Huang, Trento; Humilde, Travis S.; Isakov, Sergei V.; Jeffrey, Evan; Jiang, Zhang; Kafri, Dvir; Kechedzhi, Kostyantyn; Kelly, Julián; Klimov, Paul V.; Knysh, Sergey; Korotkov, Alejandro; Kostritsa, Fedor; Landhuis, David; Lindmark, Mike; Lucero, Erik; Lyakh, Dmitry; Mandrá, Salvatore; McClean, Jarrod R.; McEwen, Mateo; Megant, Antonio; Mi, Xiao; Michielsen, Kristel; Mohseni, Masoud; Mutus, Josh; Naamán, Ofer; Neeley, Mateo; Neill, Carlos; Niu, Murphy Yuezhen; Ostby, Eric; Petukhov, André; Platt, John C.; Quintana, Chris; Rieffel, Eleanor G.; Roushan, Pedram; Rubin, Nicolás C.; Se hundió, Daniel; Satzinger, Kevin J.; Smelyanskiy, Vadim; Sung, Kevin J.; Trevithick, Mateo D.; Vainsencher, Amit; Villalonga, Benjamín; Blanco, Teodoro; Yao, Z. Jamie; Sí, Ping; Zalcman, Adán; Neven, Hartmut; Martinis, John M. (23 de octubre de 2019). "Supremacía cuántica mediante un procesador superconductor programable". Nature . 574 (7779). Springer Science and Business Media LLC: 505–510. arXiv : 1910.11333 . doi :10.1038/s41586-019-1666-5. ISSN  0028-0836.
  49. ^ ab Nguyen, LB; Kim, Y.; Hashim, A.; Goss, N.; Marinelli, B.; Bhandari, B.; Das, D.; Naik, RK; Kreikebaum, JM; Jordan, A.; Santiago, DI; Siddiqi, I. (16 de enero de 2024). "Interacciones programables de Heisenberg entre qubits de Floquet". Nature Physics . 20 (1): 240–246. arXiv : 2211.10383 . Código Bibliográfico :2024NatPh..20..240N. doi : 10.1038/s41567-023-02326-7 .
  50. ^ ab Gambetta, Jay M.; Chow, Jerry M.; Steffen, Matthias (13 de enero de 2017). "Construcción de qubits lógicos en un sistema de computación cuántica superconductor". npj Quantum Information . 3 (1): 2. arXiv : 1510.04375 . Bibcode :2017npjQI...3....2G. doi : 10.1038/s41534-016-0004-0 .
  51. ^ Blais, Alexandre; Huang, Ren-Shou; Wallraff, Andreas; Girvin, Steven; Schoelkopf, Robert (2004). "Electrodinámica cuántica de cavidades para circuitos eléctricos superconductores: una arquitectura para la computación cuántica". Phys. Rev. A . 69 (6): 062320. arXiv : cond-mat/0402216 . Código Bibliográfico :2004PhRvA..69f2320B. doi :10.1103/PhysRevA.69.062320. S2CID  20427333.
  52. ^ Cottet, Nathanaël; Xiong, Haonan; Nguyen, Long B.; Lin, Yen-Hsiang; Manucharyan, Vladimir E. (4 de noviembre de 2021). "Estanterías electrónicas de un átomo artificial superconductor". Nature Communications . 12 (1). Springer Science and Business Media LLC. arXiv : 2008.02423 . doi :10.1038/s41467-021-26686-x. ISSN  2041-1723.
  53. ^ abcdef DiVincenzo, David (1 de febrero de 2008). "La implementación física de la computación cuántica". IBM TJ Watson Research Center . 48 (9–11): 771–783. arXiv : quant-ph/0002077 . Bibcode :2000ForPh..48..771D. doi :10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. S2CID  15439711.
  54. ^ Devoret, MH; Schoelkopf, RJ (7 de marzo de 2013). "Circuitos superconductores para información cuántica: una perspectiva". Science . 339 (6124): 1169–1174. Bibcode :2013Sci...339.1169D. doi :10.1126/science.1231930. PMID  23471399. S2CID  10123022.
  55. ^ Chow, Jerry M.; Gambetta, Jay M.; Córcoles, AD; Merkel, Seth T.; Smolin, John A.; Rigetti, Chad; Poletto, S.; Keefe, George A.; Rothwell, Mary B.; Rozen, JR; Ketchen, Mark B.; Steffen, M. (9 de agosto de 2012). "Conjunto de puertas cuánticas universales que se acercan a umbrales tolerantes a fallos con cúbits superconductores". Physical Review Letters . 109 (6): 060501. arXiv : 1202.5344 . Código Bibliográfico :2012PhRvL.109f0501C. doi :10.1103/PhysRevLett.109.060501. PMID  23006254. S2CID  39874288.
  56. ^ Niskanen, AO; Harrabi, K.; Yoshihara, F.; Nakamura, Y.; Lloyd, S.; Tsai, JS (4 de mayo de 2007). "Acoplamiento cuántico coherente ajustable de cúbits superconductores". Science . 316 (5825): 723–726. Bibcode :2007Sci...316..723N. doi :10.1126/science.1141324. PMID  17478714. S2CID  43175104.
  57. ^ Morsch, Oliver; Zurich, ETH "Transferencia cuántica con solo pulsar un botón". phys.org . Consultado el 9 de diciembre de 2022 .
  58. ^ ab Qiskit (28 de septiembre de 2022). "Cómo el primer cúbit superconductor cambió la computación cuántica para siempre". Qiskit . Consultado el 13 de diciembre de 2022 .
  59. ^ Nakamura, Y.; Pashkin, Yu A.; Tsai, JS (abril de 1999). "Control coherente de estados cuánticos macroscópicos en una caja de un solo par de Cooper". Nature . 398 (6730): 786–788. arXiv : cond-mat/9904003 . Bibcode :1999Natur.398..786N. doi :10.1038/19718. ISSN  0028-0836. S2CID  4392755.
  60. ^ "Baidu lanza una computadora cuántica superconductora y la primera solución de integración multiplataforma del mundo, poniendo la computación cuántica al alcance de la mano". www.prnewswire.com (Comunicado de prensa) . Consultado el 13 de diciembre de 2022 .
  61. ^ abcde "Hoja de ruta de IBM Quantum para construir supercomputadoras centradas en lo cuántico". Blog de investigación de IBM . 2021-02-09 . Consultado el 2022-12-13 .
  62. ^ Lardinois, Frederic (9 de noviembre de 2022). «IBM presenta su computadora cuántica Osprey de 433 qubits». TechCrunch . Consultado el 13 de diciembre de 2022 .
  63. ^ "Nuestro viaje hacia la computación cuántica". Google Quantum AI . Consultado el 13 de diciembre de 2022 .

Lectura adicional

  • Stancil, Daniel D.; Byrd, Gregory T. (2022). Principios de las computadoras cuánticas superconductoras (1.ª ed.). Hoboken, Nueva Jersey: John Wiley & Sons. ISBN 978-1-119-75072-7. OCLC  1302334194. 978-1-119-75074-1 (libro electrónico).
  • Salari, Alan (2024). Técnicas de microondas en ordenadores cuánticos superconductores (edición íntegra). Boston: Artech House. ISBN 978-1-63081-987-3. OCLC  1405187817. 978-1-63081-988-0 (libro electrónico).
  • IBM Quantum ofrece acceso a más de 20 sistemas informáticos cuánticos.
  • IBM Quantum Experience ofrece acceso gratuito para escribir algoritmos cuánticos y ejecutarlos en computadoras cuánticas de 5 qubits.
  • La hoja de ruta de IBM para la computación cuántica muestra que habrá sistemas de 65 qubits disponibles en 2020 y 127 qubits que estarán disponibles en algún momento de 2021.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Superconducting_quantum_computing&oldid=1251870759"