Adaptación de impedancia

Este artículo incluye una lista de referencias , lecturas relacionadas o enlaces externos , pero sus fuentes no están claras porque carece de citas en línea . Ayúdenos a mejorar este artículo introduciendo citas más precisas. ( Octubre de 2023 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En ingeniería eléctrica , la adaptación de impedancia es la práctica de diseñar o ajustar la impedancia de entrada o de salida de un dispositivo eléctrico para obtener un valor deseado. A menudo, el valor deseado se selecciona para maximizar la transferencia de potencia o minimizar la reflexión de la señal . Por ejemplo, la adaptación de impedancia se utiliza normalmente para mejorar la transferencia de potencia desde un transmisor de radio a través de la línea de transmisión de interconexión hasta la antena . Las señales en una línea de transmisión se transmitirán sin reflexiones si la línea de transmisión termina con una impedancia de adaptación.

Las técnicas de adaptación de impedancia incluyen transformadores , redes ajustables de resistencia total , capacitancia e inductancia o líneas de transmisión adecuadamente proporcionadas. Los dispositivos prácticos de adaptación de impedancia generalmente brindarán mejores resultados en una banda de frecuencia específica .

El concepto de adaptación de impedancia está muy extendido en la ingeniería eléctrica, pero es relevante en otras aplicaciones en las que se transfiere una forma de energía , no necesariamente eléctrica , entre una fuente y una carga, como en acústica o en óptica .

La impedancia es la oposición que opone un sistema al flujo de energía procedente de una fuente. Para señales constantes, esta impedancia también puede ser constante. Para señales variables, suele cambiar con la frecuencia. La energía implicada puede ser eléctrica , mecánica , acústica , magnética , electromagnética o térmica . El concepto de impedancia eléctrica es quizás el más conocido. La impedancia eléctrica, al igual que la resistencia eléctrica, se mide en ohmios . En general, la impedancia (símbolo: Z ) tiene un valor complejo ; esto significa que las cargas generalmente tienen un componente de resistencia (símbolo: R ) que forma la parte real y un componente de reactancia (símbolo: X ) que forma la parte imaginaria .

En casos simples (como transmisión de energía de baja frecuencia o corriente continua ) la reactancia puede ser despreciable o nula; la impedancia puede considerarse una resistencia pura, expresada como un número real. En el siguiente resumen, consideraremos el caso general en el que la resistencia y la reactancia son significativas y el caso especial en el que la reactancia es despreciable.

La coincidencia conjugada compleja se utiliza cuando se requiere una transferencia de potencia máxima , es decir,

${\displaystyle Z_{\mathsf {cargar}}=Z_{\mathsf {fuente}}^{*}\,}$

donde un superíndice * indica el conjugado complejo . Una coincidencia conjugada es diferente de una coincidencia sin reflexión cuando la fuente o la carga tienen un componente reactivo.

Si la fuente tiene un componente reactivo, pero la carga es puramente resistiva, entonces la adaptación se puede lograr agregando una reactancia de la misma magnitud pero de signo opuesto a la carga. Esta red de adaptación simple, que consta de un solo elemento , generalmente logrará una adaptación perfecta en una sola frecuencia. Esto se debe a que el elemento agregado será un capacitor o un inductor, cuya impedancia en ambos casos depende de la frecuencia y, en general, no seguirá la dependencia de la frecuencia de la impedancia de la fuente. Para aplicaciones de ancho de banda amplio , se debe diseñar una red más compleja.

Siempre que una fuente de potencia con una impedancia de salida fija , como una fuente de señal eléctrica, un transmisor de radio o un sonido mecánico (por ejemplo, un altavoz ), opera sobre una carga , la máxima potencia posible se entrega a la carga cuando la impedancia de la carga ( impedancia de carga o impedancia de entrada ) es igual al conjugado complejo de la impedancia de la fuente (es decir, su impedancia interna o impedancia de salida ). Para que dos impedancias sean conjugados complejos, sus resistencias deben ser iguales y sus reactancias deben ser iguales en magnitud pero de signos opuestos. En sistemas de baja frecuencia o CC (o sistemas con fuentes y cargas puramente resistivas) las reactancias son cero o lo suficientemente pequeñas como para ignorarlas. En este caso, la transferencia de potencia máxima ocurre cuando la resistencia de la carga es igual a la resistencia de la fuente (consulte el teorema de máxima potencia para una prueba matemática).

La adaptación de impedancia no siempre es necesaria. Por ejemplo, si entregar un alto voltaje (para reducir la degradación de la señal o el consumo de energía) es más importante que maximizar la transferencia de energía, entonces se suele utilizar el puenteo de impedancia o el puenteo de voltaje .

En los sistemas de audio más antiguos (que dependían de transformadores y redes de filtros pasivos, y se basaban en el sistema telefónico ), las resistencias de la fuente y la carga se igualaban a 600 ohmios. Una razón para esto era maximizar la transferencia de potencia, ya que no había amplificadores disponibles que pudieran restaurar la señal perdida. Otra razón era asegurar el correcto funcionamiento de los transformadores híbridos utilizados en el equipo de intercambio central para separar el habla saliente de la entrante, de modo que pudieran amplificarse o alimentarse a un circuito de cuatro cables . La mayoría de los circuitos de audio modernos, por otro lado, utilizan amplificación y filtrado activos y pueden usar conexiones de puente de voltaje para una mayor precisión. Estrictamente hablando, la igualación de impedancia solo se aplica cuando tanto los dispositivos de fuente como de carga son lineales ; sin embargo, la igualación se puede obtener entre dispositivos no lineales dentro de ciertos rangos operativos.

El ajuste de la impedancia de la fuente o de la impedancia de carga, en general, se denomina "adaptación de impedancia". Existen tres formas de mejorar un desajuste de impedancia, todas ellas denominadas "adaptación de impedancia":

• Dispositivos diseñados para presentar una carga aparente a la fuente de Z _carga  =  Z _fuente * (adaptación conjugada compleja). Dada una fuente con un voltaje fijo y una impedancia de fuente fija, el teorema de máxima potencia dice que esta es la única forma de extraer la máxima potencia de la fuente.
• Dispositivos diseñados para presentar una carga aparente de _carga Z  =  _línea Z (adaptación de impedancia compleja), para evitar ecos. Dada una fuente de línea de transmisión con una impedancia de fuente fija, esta "adaptación de impedancia sin reflexión" al final de la línea de transmisión es la única forma de evitar que los ecos se reflejen de vuelta a la línea de transmisión.
• Dispositivos destinados a presentar una resistencia aparente de fuente lo más cercana posible a cero, o presentar una tensión aparente de fuente lo más alta posible. Esta es la única forma de maximizar la eficiencia energética , por lo que se utilizan al principio de las líneas eléctricas. Este tipo de conexión de puente de impedancia también minimiza la distorsión y la interferencia electromagnética ; también se utiliza en los amplificadores de audio modernos y en los dispositivos de procesamiento de señales.

Existe una variedad de dispositivos que se utilizan entre una fuente de energía y una carga que realizan la "adaptación de impedancia". Para hacer coincidir las impedancias eléctricas, los ingenieros utilizan combinaciones de transformadores , resistencias , inductores , condensadores y líneas de transmisión . Estos dispositivos de adaptación de impedancia pasivos (y activos) están optimizados para diferentes aplicaciones e incluyen baluns , sintonizadores de antena (a veces llamados ATU o montañas rusas, debido a su apariencia), bocinas acústicas, redes de adaptación y terminadores .

A veces se utilizan transformadores para hacer coincidir las impedancias de los circuitos. Un transformador convierte la corriente alterna a un voltaje en la misma forma de onda a otro voltaje. La entrada de energía al transformador y la salida del transformador son las mismas (excepto por las pérdidas de conversión). El lado con el voltaje más bajo tiene una impedancia baja (porque tiene un número menor de vueltas) y el lado con el voltaje más alto tiene una impedancia más alta (ya que tiene más vueltas en su bobina).

Un ejemplo de este método es el de un transformador balun de televisión. Este transformador permite interconectar una línea balanceada (cable coaxial de 300 ohmios, de dos conductores ) y una línea no balanceada (cable coaxial de 75 ohmios, como el RG-6 ). Para que coincidan las impedancias, ambos cables deben estar conectados a un transformador de adaptación con una relación de vueltas de 2:1. En este ejemplo, la línea de 300 ohmios está conectada al lado del transformador con más vueltas; el cable de 75 ohmios está conectado al lado del transformador con menos vueltas. La fórmula para calcular la relación de vueltas del transformador para este ejemplo es:

${\displaystyle {\text{relación de vueltas}}={\sqrt {\frac {\text{resistencia de la fuente}}{\text{resistencia de carga}}}}}$

Las adaptaciones de impedancia resistiva son más fáciles de diseñar y se pueden lograr con un simple pad en L que consta de dos resistencias. La pérdida de potencia es una consecuencia inevitable del uso de redes resistivas y solo se utilizan (normalmente) para transferir señales de nivel de línea .

La mayoría de los dispositivos de elementos concentrados pueden adaptarse a un rango específico de impedancias de carga. Por ejemplo, para adaptar una carga inductiva a una impedancia real, se necesita utilizar un condensador. Si la impedancia de carga se vuelve capacitiva, el elemento de adaptación debe reemplazarse por un inductor. En muchos casos, existe la necesidad de utilizar el mismo circuito para adaptarse a un amplio rango de impedancia de carga y, de esta manera, simplificar el diseño del circuito. Esta cuestión se abordó con la línea de transmisión escalonada ^[1] , donde se utilizan múltiples lingotes dieléctricos de cuarto de onda colocados en serie para variar la impedancia característica de una línea de transmisión. Al controlar la posición de cada elemento, se puede adaptar una amplia gama de impedancias de carga sin tener que volver a conectar el circuito.

Los filtros se utilizan con frecuencia para lograr la adaptación de impedancia en las telecomunicaciones y la ingeniería de radio. En general, no es teóricamente posible lograr una adaptación de impedancia perfecta en todas las frecuencias con una red de componentes discretos. Las redes de adaptación de impedancia se diseñan con un ancho de banda definido, toman la forma de un filtro y utilizan la teoría de filtros en su diseño.

Las aplicaciones que requieren un ancho de banda estrecho, como los sintonizadores y transmisores de radio, pueden utilizar un filtro sintonizado simple , como un stub . Esto proporcionaría una coincidencia perfecta solo en una frecuencia específica. La coincidencia de ancho de banda amplio requiere filtros con múltiples secciones.

Una red simple de adaptación de impedancia eléctrica requiere un capacitor y un inductor. En la figura de la derecha, R ₁ > R ₂ , sin embargo, R ₁ o R ₂ pueden ser la fuente y el otro la carga. Uno de X ₁ o X ₂ debe ser un inductor y el otro debe ser un capacitor. Una reactancia está en paralelo con la fuente (o carga) y la otra está en serie con la carga (o fuente). Si una reactancia está en paralelo con la fuente , la red efectiva se adapta de alta a baja impedancia.

El análisis es el siguiente. ^[3] Considere una impedancia de fuente real de y una impedancia de carga real de . Si una reactancia está en paralelo con la impedancia de fuente, la impedancia combinada se puede escribir como:$Estilo de visualización R_{1}$$Estilo de visualización R_{2}$$Estilo de visualización X_{1}$

${\displaystyle {\frac {jR_{1}X_{1}}{R_{1}+jX_{1}}}}$

Si la parte imaginaria de la impedancia anterior se cancela con la reactancia en serie, la parte real es

${\displaystyle R_{2}={\frac {R_{1}X_{1}^{2}}{R_{1}^{2}+X_{1}^{2}}}}$

Resolviendo para$Estilo de visualización X_{1}$

${\displaystyle \left\vert X_{1}\right\vert ={\frac {R_{1}}{Q}}}$.

${\displaystyle \left\vert X_{2}\right\vert =QR_{2}}$.

dónde .${\displaystyle Q={\sqrt {\frac {R_{1}-R_{2}}{R_{2}}}}}$

Tenga en cuenta que la reactancia en paralelo tiene una reactancia negativa porque normalmente es un condensador. Esto le da a la red L la característica adicional de supresión de armónicos, ya que también es un filtro de paso bajo.${\displaystyle X_{1}}$

La conexión inversa (aumento de impedancia) es simplemente lo inverso: por ejemplo, reactancia en serie con la fuente. La magnitud de la relación de impedancia está limitada por las pérdidas de reactancia, como la Q del inductor. Se pueden conectar varias secciones en L en cascada para lograr relaciones de impedancia más altas o un mayor ancho de banda. Las redes de adaptación de líneas de transmisión se pueden modelar como infinitas secciones en L conectadas en cascada. Se pueden diseñar circuitos de adaptación óptimos para un sistema particular utilizando diagramas de Smith .

Los dispositivos de corrección del factor de potencia tienen como objetivo cancelar las características reactivas y no lineales de una carga al final de una línea eléctrica. Esto hace que la carga que ve la línea eléctrica sea puramente resistiva. Para una potencia real dada requerida por una carga, esto minimiza la corriente real suministrada a través de las líneas eléctricas y minimiza la energía desperdiciada en la resistencia de esas líneas eléctricas. Por ejemplo, se utiliza un rastreador del punto de máxima potencia para extraer la máxima potencia de un panel solar y transferirla de manera eficiente a baterías, la red eléctrica u otras cargas. El teorema de máxima potencia se aplica a su conexión "ascendente" al panel solar, por lo que emula una resistencia de carga igual a la resistencia de la fuente del panel solar. Sin embargo, el teorema de máxima potencia no se aplica a su conexión "descendente". Esa conexión es una conexión de puente de impedancia ; emula una fuente de alta tensión y baja resistencia para maximizar la eficiencia.

En la red eléctrica, la carga total suele ser inductiva . Por lo tanto, la corrección del factor de potencia se consigue más comúnmente con bancos de condensadores . Solo es necesario que la corrección se consiga en una única frecuencia, la frecuencia de la fuente de alimentación. Las redes complejas solo se requieren cuando se debe adaptar una banda de frecuencias y esta es la razón por la que los condensadores simples son todo lo que se necesita para la corrección del factor de potencia.

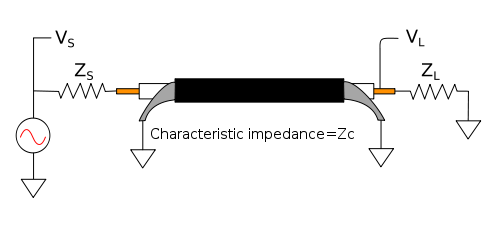
En las conexiones de RF, es conveniente que haya una adaptación de impedancias, ya que de lo contrario pueden generarse reflexiones al final de la línea de transmisión no adaptada, lo que puede provocar pérdidas dependientes de la frecuencia.

En los sistemas eléctricos que involucran líneas de transmisión (como radio y fibra óptica ), donde la longitud de la línea es larga en comparación con la longitud de onda de la señal (la señal cambia rápidamente en comparación con el tiempo que tarda en viajar desde la fuente a la carga), las impedancias en cada extremo de la línea pueden coincidir con la impedancia característica de la línea de transmisión ( ) para evitar reflexiones de la señal en los extremos de la línea. En los sistemas de radiofrecuencia (RF), un valor común para las impedancias de fuente y carga es 50 ohmios . Una carga de RF típica es una antena de plano de tierra de cuarto de onda (37 ohmios con un plano de tierra ideal).${\displaystyle Z_{c}}$

La forma general del coeficiente de reflexión de voltaje para una onda que se mueve del medio 1 al medio 2 está dada por

${\displaystyle \Gamma _{12}={Z_{2}-Z_{1} \over Z_{2}+Z_{1}}}$

mientras que el coeficiente de reflexión de voltaje para una onda que se mueve del medio 2 al medio 1 es

${\displaystyle \Gamma _{21}={Z_{1}-Z_{2} \over Z_{1}+Z_{2}}}$

${\displaystyle \Gamma _{21}=-\Gamma _{12}\,}$

Por lo tanto, el coeficiente de reflexión es el mismo (excepto el signo), sin importar desde qué dirección la onda se aproxima al límite.

También existe un coeficiente de reflexión de corriente, que es el negativo del coeficiente de reflexión de voltaje. Si la onda encuentra una abertura en el extremo de la carga, se transmiten pulsos de voltaje positivo y corriente negativo hacia la fuente (corriente negativa significa que la corriente va en la dirección opuesta). Por lo tanto, en cada límite hay cuatro coeficientes de reflexión (voltaje y corriente en un lado, y voltaje y corriente en el otro lado). Los cuatro son iguales, excepto que dos son positivos y dos son negativos. El coeficiente de reflexión de voltaje y el coeficiente de reflexión de corriente en el mismo lado tienen signos opuestos. Los coeficientes de reflexión de voltaje en lados opuestos del límite tienen signos opuestos.

Como todos son iguales excepto por el signo, es tradicional interpretar el coeficiente de reflexión como el coeficiente de reflexión de voltaje (a menos que se indique lo contrario). Cualquier extremo (o ambos extremos) de una línea de transmisión puede ser una fuente o una carga (o ambos), por lo que no hay una preferencia inherente por qué lado del límite es el medio 1 y qué lado es el medio 2. Con una sola línea de transmisión, es habitual definir el coeficiente de reflexión de voltaje para una onda incidente en el límite desde el lado de la línea de transmisión, independientemente de si una fuente o carga está conectada en el otro lado.

En una línea de transmisión, una onda viaja desde la fuente a lo largo de la línea. Supongamos que la onda choca contra un límite (un cambio abrupto en la impedancia). Una parte de la onda se refleja hacia atrás, mientras que otra parte sigue avanzando. (Supongamos que solo hay un límite, en la carga).

Dejar

${\displaystyle V_{i}\,}$y sea el voltaje y la corriente que incide en el límite desde el lado de la fuente.${\displaystyle I_{i}\,}$

${\displaystyle V_{t}\,}$y sea el voltaje y la corriente que se transmite a la carga.${\displaystyle I_{t}\,}$

${\displaystyle V_{r}\,}$y sea el voltaje y la corriente que se refleja hacia la fuente.${\displaystyle I_{r}\,}$

En el lado de la línea del límite y y en el lado de la carga donde , , , , y son fasores .${\displaystyle V_{i}=Z_{c}I_{i}\,}$${\displaystyle V_{r}=-Z_{c}I_{r}\,}$${\displaystyle V_{t}=Z_{L}I_{t}\,}$${\displaystyle V_{i}\,}$${\displaystyle V_{r}\,}$${\displaystyle V_{t}\,}$${\displaystyle I_{i}\,}$${\displaystyle I_{r}\,}$${\displaystyle I_{t}\,}$

En un límite, el voltaje y la corriente deben ser continuos, por lo tanto

${\displaystyle V_{t}=V_{i}+V_{r}\,}$

${\displaystyle I_{t}=I_{i}+I_{r}\,}$

Todas estas condiciones se cumplen mediante

${\displaystyle V_{r}=\Gamma _{TL}V_{i}\,}$

${\displaystyle I_{r}=-\Gamma _{TL}I_{i}\,}$

${\displaystyle V_{t}=(1+\Gamma _{TL})V_{i}\,}$

${\displaystyle I_{t}=(1-\Gamma _{TL})I_{i}\,}$

¿Dónde está el coeficiente de reflexión que va desde la línea de transmisión hasta la carga?${\displaystyle \Gamma _{TL}\,}$

${\displaystyle \Gamma _{TL}={Z_{L}-Z_{c} \over Z_{L}+Z_{c}}=\Gamma _{L}\,}$^{[4] [5] [6]}

En el extremo de la fuente de la línea de transmisión, puede haber ondas incidentes tanto desde la fuente como desde la línea; se puede calcular un coeficiente de reflexión para cada dirección con

${\displaystyle -\Gamma _{ST}=\Gamma _{TS}={Z_{s}-Z_{c} \over Z_{s}+Z_{c}}=\Gamma _{S}\,}$,

donde Zs es la impedancia de la fuente. La fuente de ondas incidentes desde la línea son las reflexiones desde el extremo de carga. Si la impedancia de la fuente coincide con la línea, las reflexiones desde el extremo de carga serán absorbidas en el extremo de la fuente. Si la línea de transmisión no coincide en ambos extremos, las reflexiones desde la carga se reflejarán nuevamente en la fuente y nuevamente en el extremo de carga hasta el infinito , perdiendo energía en cada tránsito de la línea de transmisión. Esto puede causar una condición de resonancia y un comportamiento fuertemente dependiente de la frecuencia. En un sistema de banda estrecha esto puede ser deseable para la coincidencia, pero generalmente no es deseable en un sistema de banda ancha.

${\displaystyle Z_{in}=Z_{c}{\frac {(1+T^{2}\Gamma _{L})}{(1-T^{2}\Gamma _{L})}}\,}$ ^[7]

donde es la función de transferencia unidireccional (de un extremo al otro) cuando la línea de transmisión coincide exactamente en la fuente y la carga. tiene en cuenta todo lo que le sucede a la señal en tránsito (incluido el retraso, la atenuación y la dispersión). Si hay una coincidencia perfecta en la carga, y${\displaystyle T\ ,}$${\displaystyle T\,}$${\displaystyle \Gamma _{L}=0\,}$${\displaystyle Z_{in}=Z_{c}\,}$

${\displaystyle V_{L}=V_{S}{\frac {T(1-\Gamma _{S})(1+\Gamma _{L})}{2(1-T^{2}\Gamma _{S}\Gamma _{L})}}\,}$

¿Dónde está el voltaje de salida del circuito abierto (o descargado) de la fuente?${\displaystyle V_{S}\,}$

Tenga en cuenta que si hay una coincidencia perfecta en ambos extremos

${\displaystyle \Gamma _{L}=0\,}$y${\displaystyle \Gamma _{S}=0\,}$

y luego

${\displaystyle V_{L}=V_{S}{\frac {T}{2}}\,}$.

Los sistemas telefónicos también utilizan impedancias adaptadas para minimizar el eco en líneas de larga distancia. Esto está relacionado con la teoría de líneas de transmisión. La adaptación también permite que la bobina híbrida telefónica (conversión de 2 a 4 cables) funcione correctamente. Como las señales se envían y reciben en el mismo circuito de dos cables a la oficina central (o central), es necesaria la cancelación en el auricular del teléfono para que no se escuche un efecto local excesivo . Todos los dispositivos utilizados en las rutas de señal telefónica dependen generalmente de impedancias adaptadas de cable, fuente y carga. En el bucle local, la impedancia elegida es de 600 ohmios (nominal). Las redes de terminación se instalan en la central para ofrecer la mejor adaptación a sus líneas de abonado. Cada país tiene su propio estándar para estas redes, pero todas están diseñadas para aproximarse a unos 600 ohmios en la banda de frecuencia de voz .

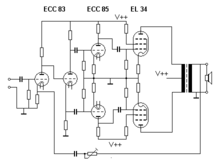
Los amplificadores de audio normalmente no igualan las impedancias, sino que proporcionan una impedancia de salida que es menor que la impedancia de carga (como < 0,1 ohmios en los amplificadores de semiconductores típicos ), para una mejor amortiguación de los altavoces . En el caso de los amplificadores de tubo de vacío , a menudo se utilizan transformadores de cambio de impedancia para obtener una impedancia de salida baja y para que el rendimiento del amplificador coincida mejor con la impedancia de carga. Algunos amplificadores de tubo tienen tomas de transformador de salida para adaptar la salida del amplificador a las impedancias típicas de los altavoces.

El transformador de salida en los amplificadores basados ​​en tubos de vacío tiene dos funciones básicas:

• Separación del componente de corriente alterna (que contiene las señales de audio) del componente de corriente continua (que suministra la fuente de alimentación ) en el circuito del ánodo de una etapa de potencia basada en válvulas de vacío. Un altavoz no debe estar sujeto a corriente continua.
• Reducción de la impedancia de salida de los pentodos de potencia (como el EL34 ) en una configuración de cátodo común .

La impedancia del altavoz en la bobina secundaria del transformador se transformará en una impedancia mayor en la bobina primaria en el circuito de los pentodos de potencia por el cuadrado de la relación de vueltas , que forma el factor de escala de impedancia .

La etapa de salida de las etapas finales basadas en semiconductores de colector común o drenaje común con MOSFET o transistores de potencia tiene una impedancia de salida muy baja. Si están correctamente balanceadas, no es necesario un transformador o un condensador electrolítico grande para separar la corriente alterna de la corriente continua.

De manera similar a lo que ocurre con las líneas de transmisión eléctrica, existe un problema de adaptación de impedancia cuando se transfiere energía sonora de un medio a otro. Si la impedancia acústica de los dos medios es muy diferente, la mayor parte de la energía sonora se reflejará (o absorberá), en lugar de transferirse a través de la frontera. El gel que se utiliza en la ecografía médica ayuda a transferir la energía acústica del transductor al cuerpo y viceversa. Sin el gel, la falta de adaptación de impedancia en el transductor-aire y la discontinuidad aire-cuerpo reflejan casi toda la energía, dejando muy poca para entrar en el cuerpo.

Los huesos del oído medio funcionan como una serie de palancas que ajustan la impedancia mecánica entre el tímpano (sobre el que actúan las vibraciones del aire) y el oído interno lleno de líquido.

Las bocinas en los sistemas de altavoces se utilizan como transformadores en circuitos eléctricos para hacer coincidir la impedancia del transductor con la impedancia del aire. Este principio se utiliza tanto en altavoces de bocina como en instrumentos musicales. Debido a que la mayoría de las impedancias de los controladores están mal adaptadas a la impedancia del aire libre a bajas frecuencias, las cajas de los altavoces están diseñadas para adaptar la impedancia y minimizar las cancelaciones de fase destructivas entre la salida de la parte delantera y trasera de un cono de altavoz. La intensidad del sonido producido en el aire desde un altavoz está directamente relacionada con la relación entre el diámetro del altavoz y la longitud de onda del sonido que se produce: los altavoces más grandes pueden producir frecuencias más bajas a un nivel más alto que los altavoces más pequeños. Los altavoces elípticos son un caso complejo, que actúa como altavoces grandes en sentido longitudinal y altavoces pequeños en sentido transversal. La adaptación de la impedancia acústica (o la falta de ella) afecta al funcionamiento de un megáfono , un eco y la insonorización .

Un efecto similar ocurre cuando la luz (o cualquier onda electromagnética) incide en la interfaz entre dos medios con diferentes índices de refracción . En el caso de los materiales no magnéticos, el índice de refracción es inversamente proporcional a la impedancia característica del material. Se puede calcular una impedancia óptica o de onda (que depende de la dirección de propagación) para cada medio y se puede utilizar en la ecuación de reflexión de la línea de transmisión.

${\displaystyle r={Z_{2}-Z_{1} \over Z_{1}+Z_{2}}}$

para calcular los coeficientes de reflexión y transmisión para la interfaz. Para dieléctricos no magnéticos, esta ecuación es equivalente a las ecuaciones de Fresnel . Las reflexiones no deseadas se pueden reducir mediante el uso de un revestimiento óptico antirreflejo .

Si un cuerpo de masa m choca elásticamente con un segundo cuerpo, la máxima transferencia de energía al segundo cuerpo se producirá cuando el segundo cuerpo tenga la misma masa m . En una colisión frontal de masas iguales, la energía del primer cuerpo se transferirá completamente al segundo cuerpo (como en la cuna de Newton, por ejemplo). En este caso, las masas actúan como "impedancias mecánicas", ^{[ dudoso – discutir ]} que deben coincidir para maximizar la transferencia de energía.

Si y son las masas de los cuerpos en movimiento y estacionario, y P es el momento del sistema (que permanece constante durante la colisión), la energía del segundo cuerpo después de la colisión será E ₂ :${\displaystyle m_{1}}$${\displaystyle m_{2}}$

${\displaystyle E_{2}={\frac {2P^{2}m_{2}}{(m_{1}+m_{2})^{2}}}}$

lo cual es análogo a la ecuación de transferencia de potencia.

Si no podemos cambiar las masas de los cuerpos, entonces podemos igualar su impedancia con una palanca. Imaginemos una pelota grande que cae al suelo y una pelota pequeña que se encuentra en el suelo. La pelota grande golpea el extremo corto de una palanca y la pelota pequeña es lanzada desde el extremo largo de la palanca. Si las longitudes de los brazos de la palanca satisfacen , entonces toda la energía se transferiría a la pelota pequeña si las colisiones son elásticas. Así es, aproximadamente, cómo funciona el oído medio (ver arriba).${\displaystyle l_{1}m_{1}=l_{2}m_{2}}$

Estos principios son útiles en la aplicación de materiales altamente energéticos (explosivos). Si se coloca una carga explosiva sobre un objetivo, la liberación repentina de energía hace que las ondas de compresión se propaguen a través del objetivo radialmente desde el contacto de la carga puntual. Cuando las ondas de compresión alcanzan áreas de alto desajuste de impedancia acústica (como el lado opuesto del objetivo), las ondas de tensión se reflejan de vuelta y crean desconchado . Cuanto mayor sea el desajuste, mayor será el efecto de arrugas y desconchado. Una carga iniciada contra una pared con aire detrás de ella causará más daño a la pared que una carga iniciada contra una pared con tierra detrás de ella.

• Timbre (señal)
• Relación de ondas estacionarias
• Transformador de aislamiento de línea

• Thomas, Robert L. Introducción práctica a la adaptación de impedancias (PDF) . Diseño de sistemas radiantes / Ingeniería aviónica, Douglas Aircraft Company . Archivado (PDF) del original el 23 de julio de 2023 . Consultado el 23 de julio de 2023 .(175 páginas)

• Adaptación de impedancia Adaptación de impedancia con la tabla de Smith