Haz gaussiano

En óptica , un haz gaussiano es un haz idealizado de radiación electromagnética cuya envolvente de amplitud en el plano transversal está dada por una función gaussiana ; esto también implica un perfil de intensidad (irradiancia) gaussiano . Este modo gaussiano transversal fundamental (o TEM ₀₀ ) describe la salida prevista de muchos láseres , ya que un haz de este tipo diverge menos y se puede enfocar mejor que cualquier otro. Cuando un haz gaussiano se reenfoca mediante una lente ideal , se produce un nuevo haz gaussiano. Los perfiles de amplitud del campo eléctrico y magnético a lo largo de un haz gaussiano circular de una longitud de onda y polarización dadas están determinados por dos parámetros: la cintura w ₀ , que es una medida del ancho del haz en su punto más estrecho, y la posición z relativa a la cintura. ^[1]

Dado que la función gaussiana es infinita en extensión, no existen haces gaussianos perfectos en la naturaleza, y los bordes de cualquier haz de este tipo quedarían cortados por cualquier lente o espejo finito. Sin embargo, la función gaussiana es una aproximación útil a un haz del mundo real para los casos en que las lentes o espejos en el haz son significativamente más grandes que el tamaño del punto w ( z ) del haz.

Fundamentalmente, la gaussiana es una solución de la ecuación axial de Helmholtz , la ecuación de onda para un campo electromagnético. Aunque existen otras soluciones, las familias de soluciones gaussianas son útiles para problemas que involucran vigas compactas.

Las ecuaciones que se muestran a continuación suponen una viga con una sección transversal circular en todos los valores de z ; esto se puede ver al notar que aparece una única dimensión transversal, r . Las vigas con secciones transversales elípticas , o con cinturas en diferentes posiciones en z para las dos dimensiones transversales ( vigas astigmáticas ) también se pueden describir como vigas gaussianas, pero con valores distintos de w ₀ y de la ubicación z = 0 para las dos dimensiones transversales x e y .

El haz gaussiano es un modo electromagnético transversal (TEM) . ^[2] La expresión matemática para la amplitud del campo eléctrico es una solución a la ecuación paraxial de Helmholtz . ^[1] Suponiendo polarización en la dirección x y propagación en la dirección + z , el campo eléctrico en notación fasorial (compleja) viene dado por:

$${\displaystyle {\mathbf {E}(r,z)}=E_{0}\,{\hat {\mathbf {x}}}\,{\frac {w_{0}}{w(z)}}\exp \left({\frac {-r^{2}}{w(z)^{2}}}\right)\exp \left(\!-i\left(kz+k{\frac {r^{2}}{2R(z)}}-\psi (z)\right)\!\right)}$$

donde ^{[1] [3]}

• r es la distancia radial desde el eje central de la viga,
• z es la distancia axial desde el foco del haz (o "cintura"),
• i es la unidad imaginaria ,
• k = 2 πn / λ es el número de onda (en radianes por metro) para una longitud de onda en el espacio libre λ , y n es el índice de refracción del medio en el que se propaga el haz,
• E ₀ = E (0, 0) , la amplitud del campo eléctrico en el origen ( r = 0 , z = 0 ),
• w ( z ) es el radio en el que las amplitudes de campo caen a 1/ e de sus valores axiales (es decir, donde los valores de intensidad caen a 1/ e ² de sus valores axiales), en el plano z a lo largo del haz,
• w ₀ = w (0) es el radio de la cintura,
• R ( z ) es el radio de curvatura de los frentes de onda del haz en z , y
• ψ ( z ) = arctan( z / z _R ) es la fase de Gouy en z , un término de fase adicional al atribuible a la velocidad de fase de la luz.

El campo eléctrico físico se obtiene a partir de la amplitud del campo fasorial dada anteriormente, multiplicando la parte real de la amplitud por un factor de tiempo: donde es la frecuencia angular de la luz y t es el tiempo. El factor de tiempo implica una convención de signos arbitraria , como se explica en Descripciones matemáticas de la opacidad § Ambigüedad conjugada compleja .$${\displaystyle \mathbf {E} _{\text{phys}}(r,z,t)=\operatorname {Re} (\mathbf {E} (r,z)\cdot e^{i\omega t}),}$$${\textstyle\omega}$

Dado que esta solución se basa en la aproximación paraxial, no es precisa para haces con una divergencia muy fuerte. La fórmula anterior es válida en la mayoría de los casos prácticos, donde w ₀ ≫ λ / n .

La distribución de intensidad (o irradiancia ) correspondiente viene dada por

$${\displaystyle I(r,z)={|E(r,z)|^{2} \sobre 2\eta }=I_{0}\left({\frac {w_{0}}{w(z)}}\right)^{2}\exp \left({\frac {-2r^{2}}{w(z)^{2}}}\right),}$$

donde la constante η es la impedancia de onda del medio en el que se propaga el haz. Para el espacio libre, η = η ₀ ≈ 377 Ω. I ₀ = | E ₀ | ² /2 η es la intensidad en el centro del haz en su cintura.

Si P ₀ es la potencia total del haz,$${\displaystyle I_{0}={2P_{0} \over \pi w_{0}^{2}}.}$$

En una posición z a lo largo del haz (medida desde el foco), el parámetro de tamaño del punto w está dado por una relación hiperbólica : ^[1] donde ^[1] se denomina rango de Rayleigh, como se analiza más adelante, y es el índice de refracción del medio.$${\displaystyle w(z)=w_{0}\,{\sqrt {1+{\left({\frac {z}{z_{\mathrm {R} }}}\right)}^{2}} },}$$$${\displaystyle z_{\mathrm {R} }={\frac {\pi w_{0}^{2}n}{\lambda }}}$$${\estilo de visualización n}$

El radio del haz w ( z ) , en cualquier posición z a lo largo del haz, está relacionado con el ancho total en la mitad del máximo (FWHM) de la distribución de intensidad en esa posición de acuerdo con: ^[4]$${\displaystyle w(z)={\frac {{\text{FWHM}}(z)}{\sqrt {2\ln 2}}}.}$$

La curvatura de los frentes de onda es máxima en la distancia de Rayleigh, z = ± z _R , a cada lado de la cintura, cruzando el cero en la cintura misma. Más allá de la distancia de Rayleigh, | z | > z _R , nuevamente disminuye en magnitud, acercándose a cero cuando z → ±∞ . La curvatura se expresa a menudo en términos de su recíproco, R , el radio de curvatura ; para un haz gaussiano fundamental, la curvatura en la posición z está dada por:

$${\displaystyle {\frac {1}{R(z)}}={\frac {z}{z^{2}+z_{\mathrm {R} }^{2}}},}$$

Entonces, el radio de curvatura R ( z ) es ^[1] Al ser el recíproco de la curvatura, el radio de curvatura invierte el signo y es infinito en la cintura de la viga donde la curvatura pasa por cero.$${\displaystyle R(z)=z[{1+{\left({\frac {z_{\mathrm {R}}}{z}}\right)}^{2}}\right].}$$

Muchos rayos láser tienen una sección transversal elíptica. También son comunes los rayos con posiciones de cintura que son diferentes para las dos dimensiones transversales, llamados rayos astigmáticos. Estos rayos se pueden tratar utilizando las dos ecuaciones de evolución anteriores, pero con valores distintos de cada parámetro para x e y y definiciones distintas del punto z = 0. La fase de Gouy es un valor único calculado correctamente sumando la contribución de cada dimensión, con una fase de Gouy dentro del rango ± π /4 aportada por cada dimensión.

Un haz elíptico invertirá su relación de elipticidad a medida que se propaga desde el campo lejano hasta la cintura. La dimensión que era mayor lejos de la cintura será menor cerca de la cintura.

Las soluciones arbitrarias de la ecuación paraxial de Helmholtz se pueden descomponer como la suma de los modos Hermite-Gaussianos (cuyos perfiles de amplitud son separables en x e y usando coordenadas cartesianas ), modos Laguerre-Gaussianos (cuyos perfiles de amplitud son separables en r y θ usando coordenadas cilíndricas ) o de manera similar como combinaciones de modos Ince-Gaussianos (cuyos perfiles de amplitud son separables en ξ y η usando coordenadas elípticas ). ^{[5] [6] [7]} En cualquier punto a lo largo del haz z estos modos incluyen el mismo factor Gaussiano que el modo Gaussiano fundamental multiplicando los factores geométricos adicionales para el modo especificado. Sin embargo, los diferentes modos se propagan con una fase Gouy diferente, por lo que el perfil transversal neto debido a una superposición de modos evoluciona en z , mientras que la propagación de cualquier modo Hermite-Gaussiano (o Laguerre-Gaussiano) individual conserva la misma forma a lo largo de un haz.

Aunque existen otras descomposiciones modales , las gaussianas son útiles para problemas que involucran haces compactos, es decir, donde la potencia óptica está bastante confinada a lo largo de un eje. Incluso cuando un láser no está operando en el modo gaussiano fundamental, su potencia generalmente se encontrará entre los modos de orden más bajo utilizando estas descomposiciones, ya que la extensión espacial de los modos de orden superior tenderá a exceder los límites del resonador (cavidad) de un láser. "Haz gaussiano" normalmente implica radiación confinada al modo gaussiano fundamental (TEM ₀₀ ).

La dependencia geométrica de los campos de un haz gaussiano está gobernada por la longitud de onda de la luz λ ( en el medio dieléctrico, si no en el espacio libre) y los siguientes parámetros del haz , todos los cuales están conectados como se detalla en las siguientes secciones.

La forma de un haz gaussiano de una longitud de onda dada λ está determinada únicamente por un parámetro, la cintura del haz w ₀ . Esta es una medida del tamaño del haz en el punto de su foco ( z = 0 en las ecuaciones anteriores) donde el ancho del haz w ( z ) (como se definió anteriormente) es el más pequeño (y también donde la intensidad en el eje ( r = 0 ) es la más grande). A partir de este parámetro se determinan los demás parámetros que describen la geometría del haz. Esto incluye el rango de Rayleigh z _R y la divergencia asintótica del haz θ , como se detalla a continuación.

La distancia de Rayleigh o rango de Rayleigh z _R se determina dado el tamaño de la cintura de un haz gaussiano:

$${\displaystyle z_{\mathrm {R} }={\frac {\pi w_{0}^{2}n}{\lambda }}.}$$

Aquí λ es la longitud de onda de la luz, n es el índice de refracción. A una distancia de la cintura igual al rango de Rayleigh z _R , el ancho w del haz es √ 2 mayor que en el foco donde w = w ₀ , la cintura del haz. Eso también implica que la intensidad en el eje ( r = 0 ) allí es la mitad de la intensidad pico (en z = 0 ). Ese punto a lo largo del haz también es donde la curvatura del frente de onda ( 1/ R ) es mayor. ^[1]

La distancia entre los dos puntos z = ± z _R se denomina parámetro confocal o profundidad de foco del haz. ^[8]

Aunque las colas de una función gaussiana nunca llegan a cero, para los fines de la siguiente discusión, se considera que el "borde" de un haz es el radio donde r = w ( z ) . Es ahí donde la intensidad ha caído a 1/ e ² de su valor en el eje. Ahora, para z ≫ z _R el parámetro w ( z ) aumenta linealmente con z . Esto significa que lejos de la cintura, el "borde" del haz (en el sentido anterior) tiene forma de cono. El ángulo entre ese cono (cuyo r = w ( z ) ) y el eje del haz ( r = 0 ) define la divergencia del haz:$${\displaystyle \theta =\lim _{z\to \infty }\arctan \left({\frac {w(z)}{z}}\right).}$$

En el caso paraxial, como hemos estado considerando, θ (en radianes) es entonces aproximadamente ^[1]$${\displaystyle \theta ={\frac {\lambda }{\pi nw_{0}}}}$$

donde n es el índice de refracción del medio a través del cual se propaga el haz y λ es la longitud de onda en el espacio libre. La dispersión angular total del haz divergente, o ángulo del vértice del cono descrito anteriormente, se expresa mediante$${\displaystyle \Theta =2\theta \,.}$$

Ese cono contiene entonces el 86% de la potencia total del haz gaussiano.

Debido a que la divergencia es inversamente proporcional al tamaño del punto, para una longitud de onda dada λ , un haz gaussiano que se enfoca en un punto pequeño diverge rápidamente a medida que se propaga lejos del foco. Por el contrario, para minimizar la divergencia de un haz láser en el campo lejano (y aumentar su intensidad máxima a grandes distancias) debe tener una gran sección transversal ( w ₀ ) en la cintura (y por lo tanto un gran diámetro donde se lanza, ya que w ( z ) nunca es menor que w ₀ ). Esta relación entre el ancho del haz y la divergencia es una característica fundamental de la difracción y de la transformada de Fourier que describe la difracción de Fraunhofer . Un haz con cualquier perfil de amplitud especificado también obedece a esta relación inversa, pero el modo gaussiano fundamental es un caso especial donde el producto del tamaño del haz en el foco y la divergencia en el campo lejano es menor que para cualquier otro caso.

Dado que el modelo de haz gaussiano utiliza la aproximación paraxial, falla cuando los frentes de onda están inclinados más de 30° con respecto al eje del haz. ^[9] De la expresión anterior para la divergencia, esto significa que el modelo de haz gaussiano solo es preciso para haces con cinturas mayores a aproximadamente 2 λ / π .

La calidad del haz láser se cuantifica mediante el producto de parámetros del haz (BPP). Para un haz gaussiano, el BPP es el producto de la divergencia del haz y el tamaño de la cintura w ₀ . El BPP de un haz real se obtiene midiendo el diámetro mínimo del haz y la divergencia de campo lejano, y tomando su producto. La relación del BPP del haz real con el de un haz gaussiano ideal en la misma longitud de onda se conoce como M ² (" M al cuadrado "). El M ² para un haz gaussiano es uno. Todos los haces láser reales tienen valores M ² mayores que uno, aunque los haces de muy alta calidad pueden tener valores muy cercanos a uno.

La apertura numérica de un haz gaussiano se define como NA = n sen θ , donde n es el índice de refracción del medio a través del cual se propaga el haz. Esto significa que el rango de Rayleigh está relacionado con la apertura numérica por $${\displaystyle z_{\mathrm {R} }={\frac {nw_{0}}{\mathrm {NA} }}.}$$

La fase de Gouy es un cambio de fase que adquiere gradualmente un haz alrededor de la región focal. En la posición z, la fase de Gouy de un haz gaussiano fundamental está dada por ^[1]$${\displaystyle \psi (z)=\arctan \left({\frac {z}{z_{\mathrm {R} }}}\right).}$$

La fase de Gouy produce un aumento de la longitud de onda aparente cerca de la cintura ( z ≈ 0 ). Por lo tanto, la velocidad de fase en esa región excede formalmente la velocidad de la luz. Ese comportamiento paradójico debe entenderse como un fenómeno de campo cercano donde la desviación de la velocidad de fase de la luz (como se aplicaría exactamente a una onda plana) es muy pequeña excepto en el caso de un haz con gran apertura numérica , en cuyo caso la curvatura de los frentes de onda (ver sección anterior) cambia sustancialmente a lo largo de la distancia de una sola longitud de onda. En todos los casos, la ecuación de onda se satisface en cada posición.

El signo de la fase de Gouy depende de la convención de signos elegida para el fasor del campo eléctrico. ^[10] Con la dependencia de e ^iωt , la fase de Gouy cambia de - π /2 a + π /2 , mientras que con la dependencia de e ^{- iωt} cambia de + π /2 a - π /2 a lo largo del eje.

En el caso de un haz gaussiano fundamental, la fase de Gouy da como resultado una discrepancia de fase neta con respecto a la velocidad de la luz que asciende a π radianes (es decir, una inversión de fase) a medida que uno se mueve desde el campo lejano de un lado de la cintura al campo lejano del otro lado. Esta variación de fase no es observable en la mayoría de los experimentos. Sin embargo, es de importancia teórica y adquiere un rango mayor para los modos gaussianos de orden superior. ^[10]

Con un haz centrado en una abertura , la potencia P que pasa a través de un círculo de radio r en el plano transversal en la posición z es ^[11] donde es la potencia total transmitida por el haz.$${\displaystyle P(r,z)=P_{0}\left[1-e^{-2r^{2}/w^{2}(z)}\right],}$$$${\displaystyle P_{0}={\frac {1}{2}}\pi I_{0}w_{0}^{2}}$$

Para un círculo de radio r = w ( z ) , la fracción de potencia transmitida a través del círculo es$${\displaystyle {\frac {P(z)}{P_{0}}}=1-e^{-2}\approx 0.865.}$$

De manera similar, aproximadamente el 90% de la potencia del haz fluirá a través de un círculo de radio r = 1,07 × w ( z ) , el 95% a través de un círculo de radio r = 1,224 × w ( z ) y el 99% a través de un círculo de radio r = 1,52 × w ( z ) . ^[11]

La intensidad máxima a una distancia axial z desde la cintura del haz se puede calcular como el límite de la potencia encerrada dentro de un círculo de radio r , dividido por el área del círculo πr ² a medida que el círculo se contrae:$${\displaystyle I(0,z)=\lim _{r\to 0}{\frac {P_{0}\left[1-e^{-2r^{2}/w^{2}(z)}\right]}{\pi r^{2}}}.}$$

El límite se puede evaluar utilizando la regla de L'Hôpital :$${\displaystyle I(0,z)={\frac {P_{0}}{\pi }}\lim _{r\to 0}{\frac {\left[-(-2)(2r)e^{-2r^{2}/w^{2}(z)}\right]}{w^{2}(z)(2r)}}={2P_{0} \over \pi w^{2}(z)}.}$$

El tamaño del punto y la curvatura de un haz gaussiano en función de z a lo largo del haz también se pueden codificar en el parámetro de haz complejo q ( z ) ^{[12] [13]} dado por:$${\displaystyle q(z)=z+iz_{\mathrm {R} }.}$$

El recíproco de q ( z ) contiene la curvatura del frente de onda y la intensidad relativa en el eje en sus partes reales e imaginarias, respectivamente: ^[12]

$${\displaystyle {1 \over q(z)}={1 \over R(z)}-i{\lambda \over n\pi w^{2}(z)}.}$$

El parámetro de haz complejo simplifica el análisis matemático de la propagación del haz gaussiano, y especialmente en el análisis de cavidades de resonadores ópticos utilizando matrices de transferencia de rayos .

Luego, utilizando esta forma, la ecuación anterior para el campo eléctrico (o magnético) se simplifica enormemente. Si llamamos u a la intensidad de campo relativa de un haz gaussiano elíptico (con los ejes elípticos en las direcciones x e y ), entonces se puede separar en x e y de acuerdo con:$${\displaystyle u(x,y,z)=u_{x}(x,z)\,u_{y}(y,z),}$$

dónde $${\displaystyle {\begin{aligned}u_{x}(x,z)&={\frac {1}{\sqrt {{q}_{x}(z)}}}\exp \left(-ik{\frac {x^{2}}{2{q}_{x}(z)}}\right),\\u_{y}(y,z)&={\frac {1}{\sqrt {{q}_{y}(z)}}}\exp \left(-ik{\frac {y^{2}}{2{q}_{y}(z)}}\right),\end{aligned}}}$$

donde q _x ( z ) y q _y ( z ) son los parámetros complejos del haz en las direcciones x e y .

Para el caso común de un perfil de viga circular , q _x ( z ) = q _y ( z ) = q ( z ) y x ² + y ² = r ² , lo que produce ^[14]$${\displaystyle u(r,z)={\frac {1}{q(z)}}\exp \left(-ik{\frac {r^{2}}{2q(z)}}\right).}$$

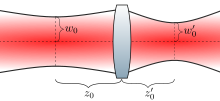
Cuando un haz gaussiano se propaga a través de una lente delgada , el haz saliente también es un haz gaussiano (distinto), siempre que el haz se desplace a lo largo del eje de simetría cilíndrico de la lente y que la lente sea más grande que el ancho del haz. La distancia focal de la lente , el radio de la cintura del haz y la posición de la cintura del haz del haz entrante se pueden utilizar para determinar el radio de la cintura del haz y la posición del haz saliente.${\displaystyle f}$${\displaystyle w_{0}}$${\displaystyle z_{0}}$${\displaystyle w_{0}'}$${\displaystyle z_{0}'}$

Como lo dedujeron Saleh y Teich, la relación entre los haces entrantes y salientes se puede encontrar considerando la fase que se agrega a cada punto del haz gaussiano a medida que viaja a través de la lente. ^[15] Un enfoque alternativo debido a Self es considerar el efecto de una lente delgada en los frentes de onda del haz gaussiano . ^[16]${\displaystyle (x,y)}$

La solución exacta al problema anterior se expresa simplemente en términos de aumento.${\displaystyle M}$

${\displaystyle {\begin{aligned}w_{0}'&=Mw_{0}\\[1.2ex](z_{0}'-f)&=M^{2}(z_{0}-f).\end{aligned}}}$

El aumento, que depende de y , viene dado por${\displaystyle w_{0}}$${\displaystyle z_{0}}$

${\displaystyle M={\frac {M_{r}}{\sqrt {1+r^{2}}}}}$

dónde

${\displaystyle r={\frac {z_{R}}{z_{0}-f}},\quad M_{r}=\left|{\frac {f}{z_{0}-f}}\right|.}$

Una expresión equivalente para la posición del haz es${\displaystyle z_{0}'}$

${\displaystyle {\frac {1}{z_{0}+{\frac {z_{R}^{2}}{(z_{0}-f)}}}}+{\frac {1}{z_{0}'}}={\frac {1}{f}}.}$

Esta última expresión deja claro que la ecuación de la lente delgada de la óptica de rayos se recupera en el límite que . También se puede observar que si entonces el haz entrante está "bien colimado" de modo que .${\displaystyle \left|\left({\tfrac {z_{R}}{z_{0}}}\right)\left({\tfrac {z_{R}}{z_{0}-f}}\right)\right|\ll 1}$${\displaystyle \left|z_{0}+{\frac {z_{R}^{2}}{z_{0}-f}}\right|\gg f}$${\displaystyle z_{0}'\approx f}$

En algunas aplicaciones es deseable utilizar una lente convergente para enfocar un haz láser en un punto muy pequeño. Matemáticamente, esto implica la minimización del aumento . Si el tamaño del haz está limitado por el tamaño de la óptica disponible, esto se logra típicamente mejor enviando el haz colimado más grande posible a través de una lente de longitud focal pequeña, es decir, maximizando y minimizando . En esta situación, es justificable hacer la aproximación , lo que implica que y obteniendo el resultado . Este resultado a menudo se presenta en la forma${\displaystyle M}$${\displaystyle z_{R}}$${\displaystyle f}$${\displaystyle z_{R}^{2}/(z_{0}-f)^{2}\gg 1}$${\displaystyle M\approx f/z_{R}}$${\displaystyle w_{0}'\approx fw_{0}/z_{R}}$

${\displaystyle {\begin{aligned}2w_{0}'&\approx {\frac {4}{\pi }}\lambda F_{\#}\\[1.2ex]z_{0}'&\approx f\end{aligned}}}$

dónde

${\displaystyle F_{\#}={\frac {f}{2w_{0}}},}$

que se obtiene después de suponer que el medio tiene índice de refracción y sustituir . Los factores de 2 se introducen debido a una preferencia común de representar el tamaño del haz por los diámetros de cintura del haz y , en lugar de los radios de cintura y .${\displaystyle n\approx 1}$${\displaystyle z_{R}=\pi w_{0}^{2}/\lambda }$${\displaystyle 2w_{0}'}$${\displaystyle 2w_{0}}$${\displaystyle w_{0}'}$${\displaystyle w_{0}}$

Como un caso especial de radiación electromagnética , los haces gaussianos (y los modos gaussianos de orden superior detallados a continuación) son soluciones a la ecuación de onda para un campo electromagnético en el espacio libre o en un medio dieléctrico homogéneo, ^[17] obtenida al combinar las ecuaciones de Maxwell para el rizo de E y el rizo de H , dando como resultado: donde c es la velocidad de la luz en el medio , y U podría referirse al vector de campo eléctrico o magnético, ya que cualquier solución específica para cualquiera determina al otro. La solución del haz gaussiano es válida solo en la aproximación paraxial , es decir, donde la propagación de la onda está limitada a direcciones dentro de un pequeño ángulo de un eje. Sin pérdida de generalidad, tomemos esa dirección como la dirección + z , en cuyo caso la solución U generalmente se puede escribir en términos de u que no tiene dependencia del tiempo y varía de manera relativamente suave en el espacio, con la variación principal correspondiendo espacialmente al número de onda k en la dirección z : ^[17]$${\displaystyle \nabla ^{2}U={\frac {1}{c^{2}}}{\frac {\partial ^{2}U}{\partial t^{2}}},}$$ $${\displaystyle U(x,y,z,t)=u(x,y,z)e^{-i(kz-\omega t)}\,{\hat {\mathbf {x} }}\,.}$$

Usando esta forma junto con la aproximación paraxial, ∂ ² u /∂ z ² puede entonces ser esencialmente ignorado. Ya que las soluciones de la ecuación de onda electromagnética sólo son válidas para polarizaciones que son ortogonales a la dirección de propagación ( z ), hemos considerado sin pérdida de generalidad que la polarización está en la dirección x de modo que ahora resolvemos una ecuación escalar para u ( x , y , z ) .

Sustituyendo esta solución en la ecuación de onda anterior se obtiene la aproximación paraxial a la ecuación de onda escalar: ^[17] Escribiendo las ecuaciones de onda en las coordenadas del cono de luz se obtiene esta ecuación sin utilizar ninguna aproximación. ^[18] Los haces gaussianos de cualquier cintura de haz w ₀ satisfacen la aproximación paraxial a la ecuación de onda escalar; esto se verifica más fácilmente expresando la onda en z en términos del parámetro de haz complejo q ( z ) como se definió anteriormente. Hay muchas otras soluciones. Como soluciones a un sistema lineal , cualquier combinación de soluciones (usando adición o multiplicación por una constante) también es una solución. La gaussiana fundamental resulta ser la que minimiza el producto del tamaño mínimo del punto y la divergencia de campo lejano, como se señaló anteriormente. Al buscar soluciones paraxiales, y en particular las que describan la radiación láser que no está en el modo gaussiano fundamental, buscaremos familias de soluciones con productos gradualmente crecientes de sus divergencias y tamaños mínimos de punto. Dos descomposiciones ortogonales importantes de este tipo son los modos de Hermite-Gauss o de Laguerre-Gauss, que corresponden a simetría rectangular y circular respectivamente, como se detalla en la siguiente sección. En ambos casos, el haz gaussiano fundamental que hemos estado considerando es el modo de orden más bajo.$${\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=2ik{\frac {\partial u}{\partial z}}.}$$

Es posible descomponer un haz paraxial coherente utilizando el conjunto ortogonal de los llamados modos Hermite-Gaussianos , cualquiera de los cuales se da por el producto de un factor en x y un factor en y . Tal solución es posible debido a la separabilidad en x e y en la ecuación de Helmholtz paraxial escrita en coordenadas cartesianas . ^[19] Así, dado un modo de orden ( l , m ) que se refiere a las direcciones x e y , la amplitud del campo eléctrico en x , y , z puede darse por: donde los factores para la dependencia de x e y se dan cada uno por: donde hemos empleado el parámetro de haz complejo q ( z ) (como se definió anteriormente) para un haz de cintura w ₀ en z desde el foco. En esta forma, el primer factor es simplemente una constante normalizadora para hacer que el conjunto de u _J sea ortonormal . El segundo factor es una normalización adicional dependiente de z que compensa la expansión de la extensión espacial del modo según w ( z )/ w ₀ (debido a los dos últimos factores). También contiene parte de la fase de Gouy. El tercer factor es una fase pura que mejora el cambio de fase de Gouy para órdenes superiores J .$${\displaystyle E(x,y,z)=u_{l}(x,z)\,u_{m}(y,z)\,\exp(-ikz),}$$$${\displaystyle u_{J}(x,z)=\left({\frac {\sqrt {2/\pi }}{2^{J}\,J!\;w_{0}}}\right)^{\!\!1/2}\!\!\left({\frac {{q}_{0}}{{q}(z)}}\right)^{\!\!1/2}\!\!\left(-{\frac {{q}^{\ast }(z)}{{q}(z)}}\right)^{\!\!J/2}\!\!H_{J}\!\left({\frac {{\sqrt {2}}x}{w(z)}}\right)\,\exp \left(\!-i{\frac {kx^{2}}{2{q}(z)}}\right),}$$

Los dos últimos factores explican la variación espacial sobre x (o y ). El cuarto factor es el polinomio de Hermite de orden J ("forma de los físicos", es decir, H ₁ ( x ) = 2 x ), mientras que el quinto explica la caída de amplitud gaussiana exp(− x ² / w ( z ) ² ) , aunque esto no es obvio utilizando el complejo q en el exponente. La expansión de ese exponencial también produce un factor de fase en x que explica la curvatura del frente de onda ( 1/ R ( z ) ) en z a lo largo del haz.

Los modos de Hermite-Gauss se designan típicamente como "TEM _lm "; el haz gaussiano fundamental puede así denominarse TEM ₀₀ (donde TEM es electromagnético transversal ). Al multiplicar u _l ( x , z ) y u _m ( y , z ) para obtener el perfil de modo 2-D, y eliminar la normalización de modo que el factor principal se denomine simplemente E ₀ , podemos escribir el modo ( l , m ) en la forma más accesible:

$${\displaystyle {\begin{aligned}E_{l,m}(x,y,z)={}&E_{0}{\frac {w_{0}}{w(z)}}\,H_{l}\!{\Bigg (}{\frac {{\sqrt {2}}\,x}{w(z)}}{\Bigg )}\,H_{m}\!{\Bigg (}{\frac {{\sqrt {2}}\,y}{w(z)}}{\Bigg )}\times {}\\&\exp \left({-{\frac {x^{2}+y^{2}}{w^{2}(z)}}}\right)\exp \left({-i{\frac {k(x^{2}+y^{2})}{2R(z)}}}\right)\times {}\\&\exp {\big (}i\psi (z){\big )}\exp(-ikz).\end{aligned}}}$$

En esta forma, el parámetro w ₀ , como antes, determina la familia de modos, en particular escalando la extensión espacial de la cintura del modo fundamental y todos los demás patrones de modos en z = 0 . Dado que w ₀ , w ( z ) y R ( z ) tienen las mismas definiciones que para el haz gaussiano fundamental descrito anteriormente. Se puede ver que con l = m = 0 obtenemos el haz gaussiano fundamental descrito anteriormente (ya que H ₀ = 1 ). La única diferencia específica en los perfiles x e y en cualquier z se debe a los factores polinomiales de Hermite para los números de orden l y m . Sin embargo, hay un cambio en la evolución de la fase de Gouy de los modos sobre z :$${\displaystyle \psi (z)=(N+1)\,\arctan \left({\frac {z}{z_{\mathrm {R} }}}\right),}$$

donde el orden combinado del modo N se define como N = l + m . Mientras que el desplazamiento de fase de Gouy para el modo gaussiano fundamental (0,0) solo cambia en ± π /2 radianes sobre todo z (y solo en ± π /4 radianes entre ± z _R ), este se incrementa por el factor N + 1 para los modos de orden superior. ^[10]

Los modos gaussianos de Hermite, con su simetría rectangular, son especialmente adecuados para el análisis modal de la radiación de láseres cuyo diseño de cavidad es asimétrico de manera rectangular. Por otra parte, los láseres y sistemas con simetría circular se pueden manejar mejor utilizando el conjunto de modos gaussianos de Laguerre que se presentan en la siguiente sección.

Los perfiles de haz que son circularmente simétricos (o láseres con cavidades que son cilíndricamente simétricas) a menudo se resuelven mejor utilizando la descomposición modal de Laguerre-Gauss. ^[6] Estas funciones se escriben en coordenadas cilíndricas utilizando polinomios de Laguerre generalizados . Cada modo transversal se etiqueta nuevamente utilizando dos números enteros, en este caso el índice radial p ≥ 0 y el índice azimutal l que puede ser positivo o negativo (o cero): ^{[20] [21]}

$${\displaystyle {\begin{aligned}u(r,\phi ,z)={}&C_{lp}^{LG}{\frac {1}{w(z)}}\left({\frac {r{\sqrt {2}}}{w(z)}}\right)^{\!|l|}\exp \!\left(\!-{\frac {r^{2}}{w^{2}(z)}}\right)L_{p}^{|l|}\!\left({\frac {2r^{2}}{w^{2}(z)}}\right)\times {}\\&\exp \!\left(\!-ik{\frac {r^{2}}{2R(z)}}\right)\exp(-il\phi )\,\exp(i\psi (z)),\end{aligned}}}$$

donde L _p ^l son los polinomios de Laguerre generalizados . C^LG
_LP-100es una constante de normalización requerida: ^[22] .$${\displaystyle C_{lp}^{LG}={\sqrt {\frac {2p!}{\pi (p+|l|)!}}}\Rightarrow \int _{0}^{2\pi }d\phi \int _{0}^{\infty }dr\;r\,|u(r,\phi ,z)|^{2}=1,}$$

w ( z ) y R ( z ) tienen las mismas definiciones que las anteriores. Al igual que con los modos Hermite-Gaussianos de orden superior, la magnitud del desplazamiento de fase de Gouy de los modos Laguerre-Gaussianos se exagera por el factor N + 1 : donde en este caso el número de modo combinado N = | l | + 2 p . Como antes, las variaciones de amplitud transversal están contenidas en los dos últimos factores en la línea superior de la ecuación, que nuevamente incluye la caída gaussiana básica en r pero ahora multiplicada por un polinomio de Laguerre. El efecto delnúmero de modo rotacional l , además de afectar al polinomio de Laguerre, está contenido principalmente en elfactor de fase exp(− ilφ ) , en el que el perfil del haz avanza (o se retrasa) en l fases 2 π completasen una rotación alrededor del haz (en φ ). Este es un ejemplo de un vórtice óptico de carga topológica l , y puede asociarse con el momento angular orbital de la luz en ese modo.$${\displaystyle \psi (z)=(N+1)\,\arctan \left({\frac {z}{z_{\mathrm {R} }}}\right),}$$

En coordenadas elípticas , se pueden escribir los modos de orden superior utilizando polinomios Ince . Los modos Ince-Gaussianos pares e impares se dan en ^[7]

$${\displaystyle u_{\varepsilon }\left(\xi ,\eta ,z\right)={\frac {w_{0}}{w\left(z\right)}}\mathrm {C} _{p}^{m}\left(i\xi ,\varepsilon \right)\mathrm {C} _{p}^{m}\left(\eta ,\varepsilon \right)\exp \left[-ik{\frac {r^{2}}{2q\left(z\right)}}-\left(p+1\right)\zeta \left(z\right)\right],}$$donde ξ y η son las coordenadas elípticas radiales y angulares definidas por C$${\displaystyle {\begin{aligned}x&={\sqrt {\varepsilon /2}}\;w(z)\cosh \xi \cos \eta ,\\y&={\sqrt {\varepsilon /2}}\;w(z)\sinh \xi \sin \eta .\end{aligned}}}$$^m-
_p( η , ε ) son los polinomios Ince pares de orden p y grado m donde ε es el parámetro de elipticidad. Los modos Hermite-Gaussiano y Laguerre-Gaussiano son un caso especial de los modos Ince-Gaussianos para ε = ∞ y ε = 0 respectivamente. ^[7]

Existe otra clase importante de modos de onda paraxiales en coordenadas cilíndricas en los que la amplitud compleja es proporcional a una función hipergeométrica confluente .

Estos modos tienen un perfil de fase singular y son funciones propias del momento angular orbital del fotón . Sus perfiles de intensidad se caracterizan por un único anillo brillante; al igual que los modos de Laguerre-Gauss, sus intensidades caen a cero en el centro (sobre el eje óptico) excepto para el modo fundamental (0,0). La amplitud compleja de un modo se puede escribir en términos de la coordenada radial normalizada (adimensional) ρ = r / w ₀ y la coordenada longitudinal normalizada Ζ = z / z _R de la siguiente manera: ^[23]

$${\displaystyle {\begin{aligned}u_{{\mathsf {p}}m}(\rho ,\phi ,\mathrm {Z} ){}={}&{\sqrt {\frac {2^{{\mathsf {p}}+|m|+1}}{\pi \Gamma ({\mathsf {p}}+|m|+1)}}}\;{\frac {\Gamma \left({\frac {\mathsf {p}}{2}}+|m|+1\right)}{\Gamma (|m|+1)}}\,i^{|m|+1}\times {}\\&\mathrm {Z} ^{\frac {\mathsf {p}}{2}}\,(\mathrm {Z} +i)^{-\left({\frac {\mathsf {p}}{2}}+|m|+1\right)}\,\rho ^{|m|}\times {}\\&\exp \left(-{\frac {i\rho ^{2}}{\mathrm {Z} +i}}\right)\,e^{im\phi }\,{}_{1}F_{1}\left(-{\frac {\mathsf {p}}{2}},|m|+1;{\frac {\rho ^{2}}{\mathrm {Z} (\mathrm {Z} +i)}}\right)\end{aligned}}}$$

donde el índice rotacional m es un entero y tiene un valor real, Γ( x ) es la función gamma y ₁ F ₁ ( a , b ; x ) es una función hipergeométrica confluente.${\displaystyle {\mathsf {p}}\geq -|m|}$

Algunas subfamilias de modos hipergeométricos-gaussianos (HyGG) pueden enumerarse como los modos Bessel-Gaussianos modificados, los modos Gaussianos exponenciales modificados ^[23] y los modos Laguerre-Gaussianos modificados.

El conjunto de modos hipergeométricos-gaussianos es sobrecompleto y no es un conjunto de modos ortogonales. A pesar de su perfil de campo complicado, los modos HyGG tienen un perfil muy simple en la cintura del haz ( z = 0 ):$${\displaystyle u(\rho ,\phi ,0)\propto \rho ^{{\mathsf {p}}+|m|}e^{-\rho ^{2}+im\phi }.}$$

• Viga de Bessel
• Viga de sombrero de copa
• Perfilador de haz láser
• Cuasióptica

• Bandrés, Miguel A.; Gutiérrez-Vega, Julio C. (2004). "Ince haces gaussianos". Optar. Lett . 29 (2). AOS: 144–146. Código Bib : 2004OptL...29..144B. doi :10.1364/OL.29.000144. PMID  14743992.
• Garg, Anupam (2012). Electromagnetismo clásico en pocas palabras . Princeton, NJ: Princeton University Press. ISBN 978-0691130187.
• Goubau, G.; Schwering, F. (1961). "Sobre la propagación guiada de haces de ondas electromagnéticas". IRE Trans . 9 (3): 248–256. Bibcode :1961ITAP....9..248G. doi :10.1109/TAP.1961.1144999. MR  0134166.
• Karimi, E.; Zito, G.; Piccirillo, B.; Marrucci, L.; Santamato, E. (2007). "Vigas hipergeométricas-gaussianas". Optar. Lett . 32 (21). AOS: 3053–3055. arXiv : 0712.0782 . Código Bib : 2007OptL...32.3053K. doi :10.1364/OL.32.003053. PMID  17975594. S2CID  46526713.
• Mandel, Leonard; Wolf, Emil (1995). Coherencia óptica y óptica cuántica . Cambridge: Cambridge University Press. ISBN 0-521-41711-2.Capítulo 5, "Haces ópticos", pág. 267.
• Pampaloni, F.; Enderlein, J. (2004). "Vigas gaussianas, hermite-gaussianas y laguerre-gaussianas: una introducción". arXiv : physics/0410021 .
• Sakpal, S.; Milione, G.; Li, M.; Nouri, M.; Shahoei, H.; LaFave, T.; Ashrafi, S.; MacFarlane, D. (2018). "Estabilidad de haces Ince-Gaussianos en fibras de pocos modos con núcleo elíptico". Opt. Lett . 43 (11): 2656–2659. Bibcode :2018OptL...43.2656S. doi :10.1364/OL.43.002656. PMID  29856389. S2CID  46921059.
• Saleh, Bahía EA; Teich, Malvin Carl (1991). Fundamentos de Fotónica . Nueva York: John Wiley & Sons. ISBN 0-471-83965-5.Capítulo 3, "Óptica de haz", págs. 80–107.
• Siegman, Anthony E. (1986). Láseres . Libros de ciencias universitarias. ISBN 0-935702-11-3.Capítulo 16.
• Svelto, Orazio (2010). Principios de los láseres (5ª ed.).
• Yariv, Amnón (1989). Electrónica cuántica (3ª ed.). Wiley. ISBN 0-471-60997-8.

• Tutorial de óptica de haz gaussiano, Newport