Centralidad

Parte de una serie sobre
Ciencia de redes
Teoría
Gráfico Red compleja Contagio Mundo pequeño Sin escala Estructura de la comunidad Filtración Evolución Controlabilidad Dibujo gráfico Capital social Análisis de enlaces Mejoramiento Reciprocidad Cierre Homofilia Transitividad Apego preferencial Teoría del equilibrio Efecto de red Influencia social
Tipos de red
Informativo (informática) Telecomunicación Transporte Social Colaboración científica Biológico Neurona artificial Interdependiente Semántico Espacial Dependencia Fluir en chip
Gráficos
Características Camarilla Componente Cortar Ciclo Estructura de datos Borde Bucle Vecindario Camino Vértice Lista  / matriz de adyacencia Listado  / matriz de incidencias Tipos Bipartito Completo Dirigido Hiper Etiquetado Multi Aleatorio Ponderado
Métrica Algoritmos
Centralidad Grado Motivo Agrupamiento Distribución de grados Asortatividad Distancia Modularidad Eficiencia
Modelos
Topología Gráfico aleatorio Erdős–Rényi Barabási–Albert Bianconi–Barabási Fitness model Watts–Strogatz Exponential random (ERGM) Random geometric (RGG) Hyperbolic (HGN) Hierarchical Stochastic block Blockmodeling Maximum entropy Soft configuration LFR Benchmark Dynamics Boolean network agent based Epidemic/SIR
Lists Categories
Topics Software Network scientists Category:Network theory Category:Graph theory
v t e

En la teoría de grafos y el análisis de redes , los indicadores de centralidad asignan números o clasificaciones a los nodos dentro de un grafo correspondientes a su posición en la red. Las aplicaciones incluyen la identificación de la(s) persona(s) más influyente(s) en una red social , nodos de infraestructura clave en Internet o redes urbanas , superpropagadores de enfermedades y redes cerebrales. ^{[1] [2]} Los conceptos de centralidad se desarrollaron por primera vez en el análisis de redes sociales , y muchos de los términos utilizados para medir la centralidad reflejan su origen sociológico . ^[3]

Los índices de centralidad son respuestas a la pregunta "¿Qué caracteriza a un vértice importante?". La respuesta se da en términos de una función de valor real en los vértices de un gráfico, donde se espera que los valores producidos proporcionen una clasificación que identifique los nodos más importantes. ^{[4] [5] [6]}

La palabra "importancia" tiene una amplia variedad de significados, lo que da lugar a muchas definiciones diferentes de centralidad. Se han propuesto dos esquemas de categorización. La "importancia" puede concebirse en relación con un tipo de flujo o transferencia a través de la red. Esto permite clasificar las centralidades según el tipo de flujo que consideran importante. ^[5] La "importancia" puede concebirse alternativamente como la participación en la cohesión de la red. Esto permite clasificar las centralidades en función de cómo miden la cohesión. ^[7] Ambos enfoques dividen las centralidades en categorías distintas. Una conclusión adicional es que una centralidad que es apropiada para una categoría a menudo "se equivocará" cuando se aplica a una categoría diferente. ^[5]

Muchas de las medidas de centralidad, aunque no todas, cuentan efectivamente la cantidad de caminos (también llamados recorridos) de algún tipo que pasan por un vértice dado; las medidas difieren en cómo se definen y cuentan los recorridos relevantes. Restringir la consideración a este grupo permite una taxonomía que coloca muchas centralidades en un espectro que va desde las relacionadas con recorridos de longitud uno (centralidad de grado) hasta recorridos infinitos (centralidad de vector propio). ^{[4] [8]} Otras medidas de centralidad, como la centralidad de intermediación , se centran no solo en la conectividad general, sino en ocupar posiciones que son fundamentales para la conectividad de la red.

Una red puede considerarse una descripción de los caminos por los que fluye algo. Esto permite una caracterización basada en el tipo de flujo y el tipo de camino codificado por la centralidad. Un flujo puede basarse en transferencias, donde cada elemento indivisible va de un nodo a otro, como una entrega de paquete que va desde el sitio de entrega hasta la casa del cliente. Un segundo caso es la duplicación en serie, en la que un elemento se replica de manera que tanto el origen como el destino lo tengan. Un ejemplo es la propagación de información a través de chismes, con la información propagándose de manera privada y con los nodos de origen y destino siendo informados al final del proceso. El último caso es la duplicación paralela, con el elemento siendo duplicado en varios enlaces al mismo tiempo, como una transmisión de radio que proporciona la misma información a muchos oyentes a la vez. ^[5]

De la misma manera, el tipo de ruta se puede limitar a geodésicas (rutas más cortas), caminos (ningún vértice se visita más de una vez), senderos (los vértices se pueden visitar varias veces, ningún borde se atraviesa más de una vez) o paseos (los vértices y los bordes se pueden visitar/atravesar varias veces). ^[5]

Se puede derivar una clasificación alternativa a partir de cómo se construye la centralidad. Esta se divide nuevamente en dos clases. Las centralidades son radiales o mediales. Las centralidades radiales cuentan los recorridos que comienzan o terminan en el vértice dado. Las centralidades de grado y de valor propio son ejemplos de centralidades radiales, que cuentan el número de recorridos de longitud uno o longitud infinita. Las centralidades mediales cuentan los recorridos que pasan por el vértice dado. El ejemplo canónico es la centralidad de intermediación de Freeman, el número de caminos más cortos que pasan por el vértice dado. ^[7]

De la misma manera, el conteo puede capturar tanto el volumen como la longitud de los paseos. El volumen es el número total de paseos del tipo dado. Los tres ejemplos del párrafo anterior caen en esta categoría. La longitud captura la distancia desde el vértice dado hasta los vértices restantes en el gráfico. La centralidad de proximidad, la distancia geodésica total desde un vértice dado hasta todos los demás vértices, es el ejemplo más conocido. ^[7] Nótese que esta clasificación es independiente del tipo de paseo contado (es decir, paseo, sendero, camino, geodésico).

Borgatti y Everett proponen que esta tipología proporciona una idea de cómo comparar mejor las medidas de centralidad. Las centralidades ubicadas en la misma casilla en esta clasificación 2x2 son lo suficientemente similares como para dar lugar a alternativas plausibles; se puede comparar razonablemente cuál es mejor para una aplicación determinada. Sin embargo, las medidas de diferentes casillas son categóricamente distintas. Cualquier evaluación de la aptitud relativa solo puede ocurrir en el contexto de predeterminar qué categoría es más aplicable, lo que hace que la comparación sea discutible. ^[7]

La caracterización por estructura de recorrido muestra que casi todas las centralidades de uso generalizado son medidas de volumen radial. Estas codifican la creencia de que la centralidad de un vértice es una función de la centralidad de los vértices con los que está asociado. Las centralidades se distinguen entre sí según cómo se define la asociación.

Bonacich demostró que si la asociación se define en términos de recorridos , entonces se puede definir una familia de centralidades en función de la longitud del recorrido considerado. ^[4] La centralidad de grado cuenta los recorridos de longitud uno, mientras que la centralidad de valor propio cuenta los recorridos de longitud infinita. También son razonables las definiciones alternativas de asociación. La centralidad alfa permite que los vértices tengan una fuente externa de influencia. La centralidad de subgrafo de Estrada propone contar solo los recorridos cerrados (triángulos, cuadrados, etc.).

El núcleo de tales medidas es la observación de que las potencias de la matriz de adyacencia del grafo dan el número de caminatas de longitud dada por esa potencia. De manera similar, la matriz exponencial también está estrechamente relacionada con el número de caminatas de una longitud dada. Una transformación inicial de la matriz de adyacencia permite una definición diferente del tipo de caminata contada. Bajo cualquiera de los enfoques, la centralidad de un vértice se puede expresar como una suma infinita, ya sea

${\displaystyle \sum _{k=0}^{\infty }A_{R}^{k}\beta ^{k}}$

para potencias matriciales o

${\displaystyle \sum _{k=0}^{\infty }{\frac {(A_{R}\beta )^{k}}{k!}}}$

para matrices exponenciales, donde

• ${\displaystyle k}$es la longitud de la caminata,
• ${\displaystyle A_{R}}$es la matriz de adyacencia transformada, y
• ${\displaystyle \beta }$es un parámetro de descuento que asegura la convergencia de la suma.

La familia de medidas de Bonacich no transforma la matriz de adyacencia. La centralidad alfa reemplaza la matriz de adyacencia con su resolvente . La centralidad del subgrafo reemplaza la matriz de adyacencia con su traza. Una conclusión sorprendente es que, independientemente de la transformación inicial de la matriz de adyacencia, todos estos enfoques tienen un comportamiento limitante común. A medida que se acerca a cero, los índices convergen a la centralidad de grado. A medida que se acerca a su valor máximo, los índices convergen a la centralidad de valor propio. ^[8]${\displaystyle \beta }$${\displaystyle \beta }$

La característica común de la mayoría de las medidas estándar mencionadas anteriormente es que evalúan la importancia de un nodo centrándose únicamente en el papel que desempeña el nodo por sí mismo. Sin embargo, en muchas aplicaciones, este enfoque es inadecuado debido a las sinergias que pueden producirse si se considera el funcionamiento de los nodos en grupos.

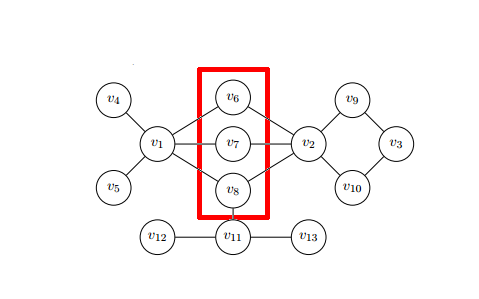
Por ejemplo, considere el problema de detener una epidemia. Mirando la imagen de arriba de la red, ¿qué nodos deberíamos vacunar? Con base en las medidas descritas previamente, queremos reconocer los nodos que son los más importantes en la propagación de la enfermedad. Los enfoques basados ​​solo en centralidades, que se centran en características individuales de los nodos, pueden no ser una buena idea. Los nodos en el cuadrado rojo, individualmente no pueden detener la propagación de la enfermedad, pero considerándolos como un grupo, vemos claramente que pueden detener la enfermedad si ha comenzado en los nodos , , y . Las centralidades de teoría de juegos intentan consultar los problemas y oportunidades descritos, utilizando herramientas de la teoría de juegos. El enfoque propuesto en ^[9] utiliza el valor de Shapley . Debido a la dureza de la complejidad temporal del cálculo del valor de Shapley, la mayoría de los esfuerzos en este dominio se dirigen a implementar nuevos algoritmos y métodos que se basan en una topología peculiar de la red o un carácter especial del problema. Tal enfoque puede llevar a reducir la complejidad temporal de exponencial a polinomial.${\displaystyle v_{1}}$${\displaystyle v_{4}}$${\displaystyle v_{5}}$

De manera similar, la distribución de autoridad del concepto de solución ( ^[10] ) aplica el índice de poder de Shapley-Shubik , en lugar del valor de Shapley , para medir la influencia directa bilateral entre los actores. La distribución es de hecho un tipo de centralidad de vector propio. Se utiliza para ordenar objetos de big data en Hu (2020), ^[11] como la clasificación de universidades de EE. UU.

Los índices de centralidad tienen dos limitaciones importantes, una obvia y otra sutil. La limitación obvia es que una centralidad que es óptima para una aplicación a menudo es subóptima para una aplicación diferente. De hecho, si esto no fuera así, no necesitaríamos tantas centralidades diferentes. Una ilustración de este fenómeno la proporciona el gráfico de cometas de Krackhardt , para el cual tres nociones diferentes de centralidad dan tres opciones diferentes del vértice más central. ^[12]

La limitación más sutil es la falacia comúnmente aceptada de que la centralidad de los vértices indica la importancia relativa de los vértices. Los índices de centralidad están diseñados explícitamente para producir una clasificación que permita indicar los vértices más importantes. ^{[4] [5]} Esto lo hacen bien, con la limitación que acabamos de señalar. No están diseñados para medir la influencia de los nodos en general. Recientemente, los físicos de redes han comenzado a desarrollar métricas de influencia de nodos para abordar este problema.

El error es doble. En primer lugar, un ranking solo ordena los vértices por importancia, no cuantifica la diferencia de importancia entre los diferentes niveles del ranking. Esto se puede mitigar aplicando la centralización de Freeman a la medida de centralidad en cuestión, que proporciona cierta información sobre la importancia de los nodos en función de las diferencias en sus puntuaciones de centralización. Además, la centralización de Freeman permite comparar varias redes comparando sus puntuaciones de centralización más altas. ^[13]

En segundo lugar, las características que identifican (correctamente) los vértices más importantes en una red/aplicación dada no necesariamente se generalizan a los vértices restantes. Para la mayoría de los otros nodos de la red, las clasificaciones pueden no tener sentido. ^{[14] [15] [16] [17]} Esto explica por qué, por ejemplo, solo los primeros resultados de una búsqueda de imágenes de Google aparecen en un orden razonable. El PageRank es una medida altamente inestable, que muestra frecuentes reversiones de clasificación después de pequeños ajustes del parámetro de salto. ^[18]

Si bien el hecho de que los índices de centralidad no se generalicen al resto de la red puede parecer contraintuitivo en un primer momento, se desprende directamente de las definiciones anteriores. Las redes complejas tienen una topología heterogénea. En la medida en que la medida óptima depende de la estructura de red de los vértices más importantes, una medida que sea óptima para dichos vértices no será óptima para el resto de la red. ^[14]

Históricamente, la primera y conceptualmente más simple es la centralidad de grado , que se define como el número de enlaces incidentes sobre un nodo (es decir, el número de vínculos que tiene un nodo). El grado se puede interpretar en términos del riesgo inmediato de un nodo de contraer lo que sea que fluya a través de la red (como un virus o alguna información). En el caso de una red dirigida (donde los vínculos tienen dirección), generalmente definimos dos medidas separadas de centralidad de grado, a saber, indegree y outdegree . En consecuencia, indegree es un recuento del número de vínculos dirigidos al nodo y outdegree es el número de vínculos que el nodo dirige a otros. Cuando los vínculos se asocian a algunos aspectos positivos como la amistad o la colaboración, indegree a menudo se interpreta como una forma de popularidad y outdegree como sociabilidad.

La centralidad de grado de un vértice , para un gráfico dado con vértices y aristas, se define como${\displaystyle v}$${\displaystyle G:=(V,E)}$${\displaystyle |V|}$${\displaystyle |E|}$

${\displaystyle C_{D}(v)=\deg(v)}$

Para calcular la centralidad de grado de todos los nodos de un gráfico se utiliza una representación de matriz de adyacencia densa del gráfico, y para los bordes se utiliza una representación de matriz dispersa .${\displaystyle \Theta (V^{2})}$ ${\displaystyle \Theta (E)}$

La definición de centralidad a nivel de nodo se puede extender a todo el grafo, en cuyo caso estamos hablando de centralización de grafo . ^[19] Sea el nodo con mayor centralidad de grado en . Sea el grafo conexo de nodos que maximiza la siguiente cantidad (siendo el nodo con mayor centralidad de grado en ):${\displaystyle v*}$${\displaystyle G}$${\displaystyle X:=(Y,Z)}$${\displaystyle |Y|}$${\displaystyle y*}$${\displaystyle X}$

${\displaystyle H=\sum _{j=1}^{|Y|}[C_{D}(y*)-C_{D}(y_{j})]}$

En consecuencia, el grado de centralización del gráfico es el siguiente:${\displaystyle G}$

${\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})]}{H}}}$

El valor de se maximiza cuando el gráfico contiene un nodo central al que están conectados todos los demás nodos (un gráfico en estrella ) y, en este caso${\displaystyle H}$${\displaystyle X}$

${\displaystyle H=(n-1)\cdot ((n-1)-1)=n^{2}-3n+2.}$

Entonces, para cualquier gráfico${\displaystyle G:=(V,E),}$

${\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})]}{|V|^{2}-3|V|+2}}}$

Además, una nueva medida global extensa para la centralidad de grado denominada Tendency to Make Hub (TMH) define lo siguiente: ^[2]

${\displaystyle {\text{TMH}}={\frac {\sum _{i=1}^{|V|}\deg(v)^{2}}{\sum _{i=1}^{|V|}\deg(v)}}}$

donde TMH aumenta con la aparición de centralidad de grado en la red.

En un gráfico conectado , la centralidad de cercanía normalizada (o cercanía ) de un nodo es la longitud promedio de la ruta más corta entre el nodo y todos los demás nodos del gráfico. Por lo tanto, cuanto más central sea un nodo, más cerca estará de todos los demás nodos.

La cercanía fue definida por Alex Bavelas (1950) como el recíproco de la lejanía , ^{[20] [21]} es decir donde es la distancia entre los vértices u y v . Sin embargo, cuando se habla de centralidad de cercanía, la gente suele referirse a su forma normalizada, dada por la fórmula anterior multiplicada por , donde es el número de nodos en el grafo${\textstyle C_{B}(v)=(\sum _{u}d(u,v))^{-1}}$${\displaystyle d(u,v)}$${\displaystyle N-1}$${\displaystyle N}$

${\displaystyle C(v)={\frac {N-1}{\sum _{u}d(u,v)}}.}$

Esta normalización permite realizar comparaciones entre nodos de grafos de diferentes tamaños. Para muchos grafos, existe una fuerte correlación entre la inversa de la cercanía y el logaritmo del grado, ^[22] donde es el grado del vértice v mientras que α y β son constantes para cada red.${\displaystyle (C(v))^{-1}\approx -\alpha \ln(k_{v})+\beta }$${\displaystyle k_{v}}$

Tomar distancias desde o hacia todos los demás nodos es irrelevante en gráficos no dirigidos, mientras que puede producir resultados totalmente diferentes en gráficos dirigidos (por ejemplo, un sitio web puede tener una alta centralidad de cercanía a partir de un enlace saliente, pero una baja centralidad de cercanía a partir de enlaces entrantes).

En un gráfico (no necesariamente conexo), la centralidad armónica invierte las operaciones de suma y recíprocas en la definición de centralidad de cercanía:

${\displaystyle H(v)=\sum _{u|u\neq v}{\frac {1}{d(u,v)}}}$

donde si no hay camino de u a v . La centralidad armónica se puede normalizar dividiendo por , donde es el número de nodos en el gráfico.${\displaystyle 1/d(u,v)=0}$${\displaystyle N-1}$${\displaystyle N}$

La centralidad armónica fue propuesta por Marchiori y Latora (2000) ^[23] y luego de forma independiente por Dekker (2005), utilizando el nombre de "centralidad valorada", ^[24] y por Rochat (2009). ^[25]

La centralidad de intermediación es una medida de centralidad de un vértice dentro de un grafo (también existe la centralidad de intermediación de aristas , que no se analiza aquí). La centralidad de intermediación cuantifica la cantidad de veces que un nodo actúa como puente a lo largo del camino más corto entre otros dos nodos. Fue introducida como una medida para cuantificar el control de un humano en la comunicación entre otros humanos en una red social por Linton Freeman . ^[26] En su concepción, los vértices que tienen una alta probabilidad de ocurrir en un camino más corto elegido aleatoriamente entre dos vértices elegidos aleatoriamente tienen una alta centralidad.

La intermediación de un vértice en un gráfico con vértices se calcula de la siguiente manera:${\displaystyle v}$${\displaystyle G:=(V,E)}$${\displaystyle V}$

1. Para cada par de vértices ( s , t ), calcule los caminos más cortos entre ellos.
2. Para cada par de vértices ( s , t ), determine la fracción de caminos más cortos que pasan por el vértice en cuestión (aquí, vértice v ).
3. Suma esta fracción sobre todos los pares de vértices ( s , t ).

De manera más compacta, la intermediación se puede representar como: ^[27]

${\displaystyle C_{B}(v)=\sum _{s\neq v\neq t\in V}{\frac {\sigma _{st}(v)}{\sigma _{st}}}}$

donde es el número total de caminos más cortos de nodo a nodo y es el número de esos caminos que pasan por . La intermediación se puede normalizar dividiendo por el número de pares de vértices sin incluir v , que para grafos dirigidos es y para grafos no dirigidos es . Por ejemplo, en un grafo en estrella no dirigido , el vértice central (que está contenido en cada camino más corto posible) tendría una intermediación de (1, si se normaliza) mientras que las hojas (que no están contenidas en ningún camino más corto) tendrían una intermediación de 0.${\displaystyle \sigma _{st}}$${\displaystyle s}$${\displaystyle t}$${\displaystyle \sigma _{st}(v)}$${\displaystyle v}$${\displaystyle (n-1)(n-2)}$${\displaystyle (n-1)(n-2)/2}$${\displaystyle (n-1)(n-2)/2}$

Desde un punto de vista de cálculo, tanto las centralidades de intermediación como las de cercanía de todos los vértices de un grafo implican calcular los caminos más cortos entre todos los pares de vértices de un grafo, lo que requiere tiempo con el algoritmo Floyd-Warshall . Sin embargo, en grafos dispersos, el algoritmo de Johnson puede ser más eficiente y requiere tiempo. En el caso de grafos no ponderados, los cálculos se pueden realizar con el algoritmo de Brandes ^[27], que requiere tiempo. Normalmente, estos algoritmos suponen que los grafos no están dirigidos y están conectados con la posibilidad de bucles y múltiples aristas. Cuando se trata específicamente de grafos de red, a menudo los grafos no tienen bucles ni múltiples aristas para mantener relaciones simples (donde las aristas representan conexiones entre dos personas o vértices). En este caso, el uso del algoritmo de Brandes dividirá las puntuaciones de centralidad finales por 2 para tener en cuenta que cada camino más corto se cuenta dos veces. ^[27]${\displaystyle O(V^{3})}$${\displaystyle O(|V||E|+|V|^{2}\log |V|)}$${\displaystyle O(|V||E|)}$

La centralidad de vector propio (también llamada centralidad propia ) es una medida de la influencia de un nodo en una red . Asigna puntuaciones relativas a todos los nodos de la red basándose en el concepto de que las conexiones a nodos con puntuaciones altas contribuyen más a la puntuación del nodo en cuestión que las conexiones iguales a nodos con puntuaciones bajas. ^{[28] [6]} El PageRank de Google y la centralidad de Katz son variantes de la centralidad de vector propio. ^[29]

Para un grafo dado con número de vértices , sea la matriz de adyacencia , es decir, si un vértice está vinculado a otro vértice , y en caso contrario. La puntuación de centralidad relativa del vértice se puede definir como:${\displaystyle G:=(V,E)}$${\displaystyle |V|}$${\displaystyle A=(a_{v,t})}$${\displaystyle a_{v,t}=1}$${\displaystyle v}$${\displaystyle t}$${\displaystyle a_{v,t}=0}$${\displaystyle v}$

${\displaystyle x_{v}={\frac {1}{\lambda }}\sum _{t\in M(v)}x_{t}={\frac {1}{\lambda }}\sum _{t\in G}a_{v,t}x_{t}}$

donde es un conjunto de vecinos de y es una constante. Con un pequeño reordenamiento, esto se puede reescribir en notación vectorial como la ecuación del vector propio .${\displaystyle M(v)}$${\displaystyle v}$${\displaystyle \lambda }$

${\displaystyle \mathbf {Ax} ={\lambda }\mathbf {x} }$

En general, habrá muchos valores propios diferentes para los cuales existe una solución de vector propio distinto de cero. Dado que las entradas en la matriz de adyacencia no son negativas, existe un único valor propio máximo, que es real y positivo, según el teorema de Perron-Frobenius . Este valor propio máximo da como resultado la medida de centralidad deseada. ^[28] El componente del vector propio relacionado proporciona entonces la puntuación de centralidad relativa del vértice en la red. El vector propio solo se define hasta un factor común, por lo que solo las razones de las centralidades de los vértices están bien definidas. Para definir una puntuación absoluta, se debe normalizar el vector propio, por ejemplo, de modo que la suma de todos los vértices sea 1 o el número total de vértices n . La iteración de potencia es uno de los muchos algoritmos de valores propios que se pueden utilizar para encontrar este vector propio dominante. ^[29] Además, esto se puede generalizar de modo que las entradas en A puedan ser números reales que representen las fortalezas de la conexión, como en una matriz estocástica .${\displaystyle \lambda }$${\displaystyle v^{th}}$${\displaystyle v}$

La centralidad de Katz ^[30] es una generalización de la centralidad de grado. La centralidad de grado mide la cantidad de vecinos directos y la centralidad de Katz mide la cantidad de todos los nodos que se pueden conectar a través de un camino, mientras que las contribuciones de los nodos distantes se penalizan. Matemáticamente, se define como

${\displaystyle x_{i}=\sum _{k=1}^{\infty }\sum _{j=1}^{N}\alpha ^{k}(A^{k})_{ji}}$

donde es un factor de atenuación en .${\displaystyle \alpha }$${\displaystyle (0,1)}$

La centralidad de Katz puede considerarse una variante de la centralidad de vector propio. Otra forma de centralidad de Katz es

${\displaystyle x_{i}=\alpha \sum _{j=1}^{N}a_{ij}(x_{j}+1).}$

En comparación con la expresión de centralidad del vector propio, se reemplaza por ${\displaystyle x_{j}}$${\displaystyle x_{j}+1.}$

Se muestra que ^[31] el vector propio principal (asociado con el valor propio más grande de , la matriz de adyacencia) es el límite de la centralidad de Katz a medida que se aproxima desde abajo.${\displaystyle A}$${\displaystyle \alpha }$${\displaystyle {\tfrac {1}{\lambda }}}$

PageRank satisface la siguiente ecuación

${\displaystyle x_{i}=\alpha \sum _{j}a_{ji}{\frac {x_{j}}{L(j)}}+{\frac {1-\alpha }{N}},}$

dónde

${\displaystyle L(j)=\sum _{i}a_{ji}}$

es el número de vecinos del nodo (o número de enlaces salientes en un gráfico dirigido). En comparación con la centralidad del vector propio y la centralidad de Katz, una diferencia importante es el factor de escala . Otra diferencia entre PageRank y la centralidad del vector propio es que el vector PageRank es un vector propio de la izquierda (nótese que el factor tiene los índices invertidos). ^[32]${\displaystyle j}$${\displaystyle L(j)}$${\displaystyle a_{ji}}$

Existen numerosas medidas de centralidad para determinar la "importancia" de un único nodo en una red compleja. Sin embargo, estas medidas cuantifican la importancia de un nodo en términos puramente topológicos, y el valor del nodo no depende de su "estado" de ninguna manera. Permanece constante independientemente de la dinámica de la red. Esto es cierto incluso para las medidas de intermediación ponderadas. Sin embargo, un nodo puede perfectamente estar ubicado centralmente en términos de centralidad de intermediación u otra medida de centralidad, pero puede no estar ubicado "centralmente" en el contexto de una red en la que hay percolación. La percolación de un "contagio" ocurre en redes complejas en varios escenarios. Por ejemplo, una infección viral o bacteriana puede propagarse a través de redes sociales de personas, conocidas como redes de contacto. La propagación de una enfermedad también puede considerarse en un nivel más alto de abstracción, contemplando una red de ciudades o centros de población, conectados por carreteras, ferrocarriles o enlaces aéreos. Los virus informáticos pueden propagarse a través de redes informáticas. Los rumores o noticias sobre ofertas y acuerdos comerciales también pueden propagarse a través de redes sociales de personas. En todos estos escenarios, un "contagio" se propaga a través de los vínculos de una red compleja, alterando los "estados" de los nodos a medida que se propaga, ya sea recuperable o no. Por ejemplo, en un escenario epidemiológico, los individuos pasan del estado "susceptible" al "infectado" a medida que se propaga la infección. Los estados que pueden adoptar los nodos individuales en los ejemplos anteriores podrían ser binarios (como recibir/no recibir una noticia), discretos (susceptible/infectado/recuperado) o incluso continuos (como la proporción de personas infectadas en una ciudad), a medida que se propaga el contagio. La característica común en todos estos escenarios es que la propagación del contagio da como resultado el cambio de estados de los nodos en las redes. La centralidad de percolación (CP) se propuso con esto en mente, que mide específicamente la importancia de los nodos en términos de ayudar a la percolación a través de la red. Esta medida fue propuesta por Piraveenan et al. ^[33]

La centralidad de percolación se define para un nodo determinado, en un momento determinado, como la proporción de "caminos de percolación" que pasan por ese nodo. Un "camino de percolación" es un camino más corto entre un par de nodos, donde el nodo de origen está percolado (por ejemplo, infectado). El nodo de destino puede estar percolado o no percolado, o en un estado parcialmente percolado.

${\displaystyle PC^{t}(v)={\frac {1}{N-2}}\sum _{s\neq v\neq r}{\frac {\sigma _{sr}(v)}{\sigma _{sr}}}{\frac {{x^{t}}_{s}}{{\sum {[{x^{t}}_{i}}]}-{x^{t}}_{v}}}}$

donde es el número total de caminos más cortos de nodo a nodo y es el número de esos caminos que pasan por . El estado de percolación del nodo en el momento se denota por y dos casos especiales son cuando que indica un estado no percolado en el momento mientras que cuando que indica un estado completamente percolado en el momento . Los valores intermedios indican estados parcialmente percolados (por ejemplo, en una red de municipios, este sería el porcentaje de personas infectadas en ese municipio).${\displaystyle \sigma _{sr}}$${\displaystyle s}$${\displaystyle r}$${\displaystyle \sigma _{sr}(v)}$${\displaystyle v}$${\displaystyle i}$${\displaystyle t}$${\displaystyle {x^{t}}_{i}}$${\displaystyle {x^{t}}_{i}=0}$${\displaystyle t}$${\displaystyle {x^{t}}_{i}=1}$${\displaystyle t}$

Los pesos asociados a las rutas de percolación dependen de los niveles de percolación asignados a los nodos de origen, basándose en la premisa de que cuanto mayor sea el nivel de percolación de un nodo de origen, más importantes son las rutas que se originan en ese nodo. Por lo tanto, los nodos que se encuentran en rutas más cortas que se originan en nodos altamente percolados son potencialmente más importantes para la percolación. La definición de PC también se puede ampliar para incluir los pesos de los nodos de destino. Los cálculos de centralidad de percolación se ejecutan en el tiempo con una implementación eficiente adoptada del algoritmo rápido de Brandes y, si el cálculo necesita considerar los pesos de los nodos de destino, el peor tiempo posible es .${\displaystyle O(NM)}$${\displaystyle O(N^{3})}$

La centralidad entre camarillas de un solo nodo en un grafo complejo determina la conectividad de un nodo con diferentes camarillas . Un nodo con alta conectividad entre camarillas facilita la propagación de información o enfermedad en un grafo. Las camarillas son subgrafos en los que cada nodo está conectado a todos los demás nodos de la camarilla. La conectividad entre camarillas de un nodo para un grafo dado con vértices y aristas se define como donde es el número de camarillas a las que pertenece el vértice. Esta medida fue utilizada por Faghani en 2013 ^[34] pero fue propuesta por primera vez por Everett y Borgatti en 1998 donde la llamaron centralidad de superposición de camarillas.${\displaystyle v}$${\displaystyle G:=(V,E)}$${\displaystyle |V|}$${\displaystyle |E|}$${\displaystyle X(v)}$${\displaystyle X(v)}$${\displaystyle v}$

La centralización de cualquier red es una medida de cuán central es su nodo más central en relación con cuán centrales son todos los demás nodos. ^[13] Las medidas de centralización entonces (a) calculan la suma de las diferencias en centralidad entre el nodo más central en una red y todos los demás nodos; y (b) dividen esta cantidad por la suma teóricamente más grande de tales diferencias en cualquier red del mismo tamaño. ^[13] Por lo tanto, cada medida de centralidad puede tener su propia medida de centralización. Definida formalmente, si es cualquier medida de centralidad del punto , si es la medida más grande de tal tipo en la red, y si:${\displaystyle C_{x}(p_{i})}$${\displaystyle i}$${\displaystyle C_{x}(p_{*})}$

${\displaystyle \max \sum _{i=1}^{N}(C_{x}(p_{*})-C_{x}(p_{i}))}$

es la mayor suma de diferencias en la centralidad de puntos para cualquier gráfico con el mismo número de nodos, entonces la centralización de la red es: ^[13]${\displaystyle C_{x}}$

${\displaystyle C_{x}={\frac {\sum _{i=1}^{N}(C_{x}(p_{*})-C_{x}(p_{i}))}{\max \sum _{i=1}^{N}(C_{x}(p_{*})-C_{x}(p_{i}))}}.}$

El concepto se debe a Linton Freeman .

Para obtener mejores resultados en el ranking de los nodos de una red dada, en ^[35] se utilizan medidas de disimilitud (propias de la teoría de clasificación y minería de datos) para enriquecer las medidas de centralidad en redes complejas. Esto se ilustra con la centralidad de vectores propios , calculando la centralidad de cada nodo a través de la solución del problema de valores propios.

${\displaystyle W\mathbf {c} =\lambda \mathbf {c} }$

donde (producto de coordenadas) y es una matriz de disimilitud arbitraria , definida a través de una medida de disimilitud, por ejemplo, la disimilitud de Jaccard dada por${\displaystyle W_{ij}=A_{ij}D_{ij}}$${\displaystyle D_{ij}}$

${\displaystyle D_{ij}=1-{\dfrac {|V^{+}(i)\cap V^{+}(j)|}{|V^{+}(i)\cup V^{+}(j)|}}}$

Donde esta medida nos permite cuantificar la contribución topológica (por eso se llama centralidad de contribución) de cada nodo a la centralidad de un nodo dado, teniendo mayor peso/relevancia aquellos nodos con mayor disimilitud, ya que estos permiten al nodo dado acceder a nodos a los que por sí mismo no puede acceder directamente.

Cabe destacar que no es negativo porque y son matrices no negativas, por lo que podemos usar el teorema de Perron-Frobenius para asegurar que el problema anterior tiene una solución única para λ  =  λ _max con c no negativo, lo que nos permite inferir la centralidad de cada nodo en la red. Por lo tanto, la centralidad del i-ésimo nodo es${\displaystyle W}$${\displaystyle A}$${\displaystyle D}$

${\displaystyle c_{i}={\dfrac {1}{n}}\sum _{j=1}^{n}W_{ij}c_{j},\,\,\,\,\,\,i=1,\cdots ,n}$

donde es el número de nodos en la red. En ^[36] se probaron varias medidas de disimilitud y redes obteniendo mejores resultados en los casos estudiados.${\displaystyle n}$

Las redes de transporte, como las redes de carreteras y las redes ferroviarias, se estudian ampliamente en la ciencia del transporte y la planificación urbana. Varios estudios recientes se han centrado en el uso de medidas de centralidad para analizar las redes de transporte. Si bien muchos de estos estudios simplemente utilizan medidas de centralidad genéricas como la centralidad de intermediación, también se han definido medidas de centralidad personalizadas específicamente para el análisis de redes de transporte. Entre ellas, destaca la centralidad del transporte . ^[37]

La centralidad de transporte mide la suma de las proporciones de las rutas de pares de nodos en una red que pasan por el nodo en cuestión. En este sentido, es similar a la centralidad de intermediación. Sin embargo, a diferencia de la centralidad de intermediación, que solo considera las rutas más cortas, la centralidad de transporte considera todas las rutas posibles entre un par de nodos. Por lo tanto, la centralidad de transporte es una versión genérica de la centralidad de intermediación y, en determinadas condiciones, se reduce a la centralidad de intermediación.

La centralidad de transporte de un nodo dado v se define como: ^[37]

${\displaystyle TC(v)=1/((N-1)(N-2))\Sigma _{s\neq v\neq t}{\frac {\Sigma _{i\in P_{s,t}^{v}}e^{-\beta C_{s,t}^{i}}}{\Sigma _{j\in P_{s,t}^{v}}e^{-\beta C_{s,t}^{j}}}}}$

• Centralidad alfa
• Estructura núcleo-periferia
• Distancia en gráficos

• Koschützki, D.; Lehmann, KA; Peeters, L.; Richter, S.; Tenfelde-Podehl, D. y Zlotowski, O. (2005) Centrality Indices. En Brandes, U. y Erlebach, T. (Eds.) Network Analysis: Methodological Foundations , págs. 16–61, LNCS 3418, Springer-Verlag.