Gravedad de la Tierra
Este artículo necesita citas adicionales para su verificación . ( septiembre de 2024 ) |

La gravedad de la Tierra , denotada por g , es la aceleración neta que se imparte a los objetos debido al efecto combinado de la gravitación (de la distribución de masa dentro de la Tierra ) y la fuerza centrífuga (de la rotación de la Tierra ). [2] [3] Es una cantidad vectorial , cuya dirección coincide con una plomada y la fuerza o magnitud viene dada por la norma .
En unidades del SI , esta aceleración se expresa en metros por segundo al cuadrado (en símbolos, m / s2 o m·s −2 ) o, equivalentemente, en newtons por kilogramo (N/kg o N·kg −1 ). Cerca de la superficie de la Tierra, la aceleración debida a la gravedad, con una precisión de 2 cifras significativas , es de 9,8 m/s2 ( 32 ft / s2 ). Esto significa que, ignorando los efectos de la resistencia del aire , la velocidad de un objeto que cae libremente aumentará aproximadamente 9,8 metros por segundo (32 ft/s) cada segundo. Esta cantidad a veces se denomina informalmente g pequeña (en contraste, la constante gravitacional G se conoce como G mayúscula ).
La fuerza precisa de la gravedad de la Tierra varía según la ubicación. El valor acordado para la gravedad estándar es 9,80665 m/s 2 (32,1740 ft/s 2 ) por definición. [4] Esta cantidad se denota de diversas formas como g n , g e (aunque esto a veces significa la gravedad normal en el ecuador, 9,7803267715 m/s 2 (32,087686258 ft/s 2 )), [5] g 0 o simplemente g (que también se utiliza para el valor local variable).
El peso de un objeto sobre la superficie de la Tierra es la fuerza que se ejerce hacia abajo sobre ese objeto, dada por la segunda ley de movimiento de Newton , o F = m a ( fuerza = masa × aceleración ). La aceleración gravitacional contribuye a la aceleración total de la gravedad, pero otros factores, como la rotación de la Tierra, también contribuyen y, por lo tanto, afectan el peso del objeto. La gravedad normalmente no incluye la atracción gravitatoria de la Luna y el Sol, que se tienen en cuenta en términos de efectos de marea .
Variación de magnitud
Una esfera perfecta que no rota y cuya densidad de masa varía únicamente con la distancia al centro ( simetría esférica ) produciría un campo gravitatorio de magnitud uniforme en todos los puntos de su superficie . La Tierra rota y tampoco es esféricamente simétrica; más bien, es ligeramente más plana en los polos y abultada en el ecuador: un esferoide achatado . En consecuencia, hay ligeras desviaciones en la magnitud de la gravedad a lo largo de su superficie.
La gravedad en la superficie de la Tierra varía alrededor de un 0,7%, desde 9,7639 m/s 2 en el Nevado Huascarán en Perú hasta 9,8337 m/s 2 en la superficie del Océano Ártico . [6] En las grandes ciudades, varía desde 9,7806 m/s 2 [7] en Kuala Lumpur , Ciudad de México y Singapur hasta 9,825 m/s 2 en Oslo y Helsinki .
Valor convencional
En 1901, la tercera Conferencia General de Pesos y Medidas definió una aceleración gravitacional estándar para la superficie de la Tierra: g n = 9,80665 m/s 2 . Se basó en mediciones realizadas en el Pavillon de Breteuil cerca de París en 1888, con una corrección teórica aplicada para convertir a una latitud de 45° al nivel del mar. [8] Por lo tanto, esta definición no es un valor de ningún lugar en particular ni un promedio cuidadosamente calculado, sino un acuerdo sobre un valor que se utilizará si no se conoce o no es importante un mejor valor local real. [9] También se utiliza para definir las unidades kilogramo fuerza y libra fuerza .
Latitud

La superficie de la Tierra está en rotación, por lo que no es un sistema de referencia inercial . En latitudes más cercanas al Ecuador, la fuerza centrífuga hacia afuera producida por la rotación de la Tierra es mayor que en latitudes polares. Esto contrarresta la gravedad de la Tierra en un pequeño grado (hasta un máximo del 0,3 % en el Ecuador) y reduce la aceleración aparente hacia abajo de los objetos que caen.
La segunda razón principal de la diferencia de gravedad en distintas latitudes es que el abultamiento ecuatorial de la Tierra (causado también por la fuerza centrífuga de la rotación) hace que los objetos en el Ecuador estén más alejados del centro del planeta que los objetos en los polos. La fuerza debida a la atracción gravitatoria entre dos masas (un trozo de la Tierra y el objeto que se pesa) varía inversamente con el cuadrado de la distancia entre ellas. La distribución de masa también es diferente debajo de alguien en el Ecuador y debajo de alguien en un polo. El resultado neto es que un objeto en el Ecuador experimenta una atracción gravitatoria más débil que un objeto en uno de los polos.
En conjunto, el abultamiento ecuatorial y los efectos de la fuerza centrífuga de la superficie debido a la rotación significan que la gravedad a nivel del mar aumenta de aproximadamente 9,780 m/s2 en el ecuador a aproximadamente 9,832 m/s2 en los polos, por lo que un objeto pesará aproximadamente un 0,5% más en los polos que en el ecuador. [2] [10]
Altitud

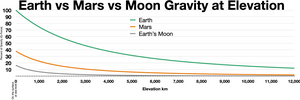
La gravedad disminuye con la altitud a medida que uno se eleva sobre la superficie de la Tierra, porque una mayor altitud significa una mayor distancia desde el centro de la Tierra. En igualdad de condiciones, un aumento de altitud desde el nivel del mar hasta los 9.000 metros (30.000 pies) provoca una disminución del peso de aproximadamente el 0,29 %. (Un factor adicional que afecta al peso aparente es la disminución de la densidad del aire en altitud, que reduce la flotabilidad de un objeto. [11] Esto aumentaría el peso aparente de una persona a una altitud de 9.000 metros en aproximadamente un 0,08 %).
Es un error muy común creer que los astronautas en órbita carecen de peso porque han volado lo suficientemente alto como para escapar de la gravedad de la Tierra. De hecho, a una altitud de 400 kilómetros (250 millas), equivalente a una órbita típica de la Estación Espacial Internacional , la gravedad sigue siendo casi un 90% tan fuerte como en la superficie de la Tierra. La ingravidez se produce en realidad porque los objetos en órbita están en caída libre . [12]
El efecto de la elevación del terreno depende de la densidad del mismo (véase la sección Corrección de losas). Una persona que vuela a 9.100 m (30.000 pies) sobre el nivel del mar sobre montañas sentirá más gravedad que alguien que se encuentre a la misma altura pero sobre el mar. Sin embargo, una persona que se encuentre sobre la superficie de la Tierra sentirá menos gravedad cuando la altura sea mayor.
La siguiente fórmula aproxima la variación de la gravedad de la Tierra con la altitud:
Dónde
- g h es la aceleración gravitacional a la altura h sobre el nivel del mar.
- R e es el radio medio de la Tierra .
- g 0 es la aceleración gravitacional estándar .
La fórmula trata a la Tierra como una esfera perfecta con una distribución de masa radialmente simétrica; más adelante se analiza un tratamiento matemático más preciso.
Profundidad



Se puede obtener un valor aproximado de la gravedad a una distancia r del centro de la Tierra suponiendo que la densidad de la Tierra es esféricamente simétrica. La gravedad depende únicamente de la masa dentro de la esfera de radio r . Todas las contribuciones del exterior se cancelan como consecuencia de la ley de gravitación del cuadrado inverso . Otra consecuencia es que la gravedad es la misma que si toda la masa estuviera concentrada en el centro. Por lo tanto, la aceleración gravitatoria en este radio es [14]
donde G es la constante gravitacional y M ( r ) es la masa total encerrada dentro del radio r . Si la Tierra tuviera una densidad constante ρ , la masa sería M ( r ) = (4/3) πρr 3 y la dependencia de la gravedad con la profundidad sería
La gravedad g′ a una profundidad d se expresa mediante g′ = g (1 − d / R ) donde g es la aceleración debida a la gravedad en la superficie de la Tierra, d es la profundidad y R es el radio de la Tierra . Si la densidad disminuye linealmente con el aumento del radio desde una densidad ρ 0 en el centro hasta ρ 1 en la superficie, entonces ρ ( r ) = ρ 0 − ( ρ 0 − ρ 1 ) r / R , y la dependencia sería
La dependencia real de la profundidad de la densidad y la gravedad, inferida a partir de los tiempos de viaje sísmico (véase la ecuación de Adams-Williamson ), se muestra en los gráficos siguientes.
Topografía y geología local
Las diferencias locales en la topografía (como la presencia de montañas), la geología (como la densidad de rocas en las cercanías) y la estructura tectónica más profunda causan diferencias locales y regionales en el campo gravitacional de la Tierra, conocidas como anomalías gravitacionales . [15] Algunas de estas anomalías pueden ser muy extensas, dando como resultado abultamientos en el nivel del mar y haciendo que los relojes de péndulo pierdan la sincronización.
El estudio de estas anomalías constituye la base de la geofísica gravitacional . Las fluctuaciones se miden con gravímetros de alta sensibilidad , se resta el efecto de la topografía y otros factores conocidos y a partir de los datos resultantes se extraen conclusiones. En la actualidad, los buscadores de oro utilizan estas técnicas para encontrar yacimientos de petróleo y minerales . Las rocas más densas (que a menudo contienen minerales ) provocan campos gravitatorios locales más altos de lo normal en la superficie de la Tierra. Las rocas sedimentarias menos densas provocan lo contrario.
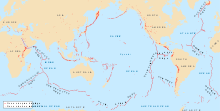
Existe una fuerte correlación entre el mapa de derivación de la gravedad de la Tierra de NASA GRACE con las posiciones de actividad volcánica reciente, expansión de dorsales y volcanes: estas regiones tienen una gravitación más fuerte que las predicciones teóricas.
Otros factores
En el aire o en el agua, los objetos experimentan una fuerza de flotabilidad que reduce la fuerza aparente de la gravedad (medida por el peso de un objeto). La magnitud del efecto depende de la densidad del aire (y, por lo tanto, de la presión del aire) o de la densidad del agua, respectivamente; consulte Peso aparente para obtener más detalles.
Los efectos gravitacionales de la Luna y el Sol (también causantes de las mareas ) tienen un efecto muy pequeño en la fuerza aparente de la gravedad de la Tierra, dependiendo de sus posiciones relativas; las variaciones típicas son de 2 μm/s2 ( 0,2 mGal ) a lo largo de un día.
Dirección

La aceleración de la gravedad es una cantidad vectorial , con dirección además de magnitud . En una Tierra con simetría esférica, la gravedad apuntaría directamente hacia el centro de la esfera. Como la figura de la Tierra es ligeramente más plana, existen en consecuencia desviaciones significativas en la dirección de la gravedad: esencialmente la diferencia entre la latitud geodésica y la latitud geocéntrica . Las desviaciones más pequeñas, llamadas deflexión vertical , son causadas por anomalías de masa locales, como las montañas.
Valores comparativos a nivel mundial
Existen herramientas para calcular la fuerza de la gravedad en varias ciudades alrededor del mundo. [16] El efecto de la latitud se puede ver claramente con la gravedad en ciudades de alta latitud: Anchorage (9,826 m/s 2 ), Helsinki (9,825 m/s 2 ), siendo aproximadamente un 0,5% mayor que en ciudades cercanas al ecuador: Kuala Lumpur (9,776 m/s 2 ). El efecto de la altitud se puede ver en la Ciudad de México (9,776 m/s 2 ; altitud 2.240 metros (7.350 pies)), y comparando Denver (9,798 m/s 2 ; 1.616 metros (5.302 pies)) con Washington, DC (9,801 m/s 2 ; 30 metros (98 pies)), ambas cerca de 39° N. Los valores medidos se pueden obtener de las Tablas físicas y matemáticas de TM Yarwood y F. Castle, Macmillan, edición revisada de 1970. [17]
| Ubicación | m/ s2 | pies/s 2 | Ubicación | m/ s2 | pies/s 2 | Ubicación | m/ s2 | pies/s 2 | Ubicación | m/ s2 | pies/s 2 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anclaje | 9.826 | 32.24 | Helsinki | 9.825 | 32.23 | Oslo | 9.825 | 32.23 | Copenhague | 9.821 | 32.22 | |||
| Estocolmo | 9.818 | 32.21 | Manchester | 9.818 | 32.21 | Ámsterdam | 9.817 | 32.21 | Kotagiri | 9.817 | 32.21 | |||
| Birmingham | 9.817 | 32.21 | Londres | 9.816 | 32.20 | Bruselas | 9.815 | 32.20 | Fráncfort | 9.814 | 32.20 | |||
| Seattle | 9.811 | 32,19 | París | 9.809 | 32.18 | Montreal | 9.809 | 32.18 | Vancouver | 9.809 | 32.18 | |||
| Estanbul | 9.808 | 32.18 | Toronto | 9.807 | 32.18 | Zúrich | 9.807 | 32.18 | Ottawa | 9.806 | 32.17 | |||
| Skopie | 9.804 | 32.17 | Chicago | 9.804 | 32.17 | Roma | 9.803 | 32.16 | Wellington | 9.803 | 32.16 | |||
| Ciudad de Nueva York | 9.802 | 32.16 | Lisboa | 9.801 | 32.16 | Washington, D.C. | 9.801 | 32.16 | Atenas | 9.800 | 32.15 | |||
| Madrid | 9.800 | 32.15 | Melbourne | 9.800 | 32.15 | Auckland | 9.799 | 32.15 | Denver | 9.798 | 32.15 | |||
| Tokio | 9.798 | 32.15 | Buenos Aires | 9.797 | 32.14 | Sídney | 9.797 | 32.14 | Nicosia | 9.797 | 32.14 | |||
| Los Ángeles | 9.796 | 32.14 | Ciudad del Cabo | 9.796 | 32.14 | Perth | 9.794 | 32.13 | Ciudad de Kuwait | 9.792 | 32.13 | |||
| Taipéi | 9.790 | 32.12 | Río de Janeiro | 9.788 | 32.11 | la Habana | 9.786 | 32.11 | Calcuta | 9.785 | 32.10 | |||
| Hong Kong | 9.785 | 32.10 | Bangkok | 9.780 | 32.09 | Manila | 9.780 | 32.09 | Jacarta | 9.777 | 32.08 | |||
| Kuala Lumpur | 9.776 | 32.07 | Singapur | 9.776 | 32.07 | Ciudad de México | 9.776 | 32.07 | Kandy | 9.775 | 32.07 |
Modelos matemáticos
Si el terreno está al nivel del mar, podemos estimar, para el Sistema de Referencia Geodésico 1980, la aceleración en latitud :
Esta es la Fórmula Internacional de Gravedad de 1967, la Fórmula del Sistema de Referencia Geodésico de 1967, la ecuación de Helmert o fórmula de Clairaut . [18]
Una fórmula alternativa para g como función de la latitud es la Fórmula de Gravedad Elipsoidal del WGS ( Sistema Geodésico Mundial ) 84 : [19]
dónde,
- son los semiejes ecuatorial y polar, respectivamente;
- es la excentricidad del esferoide , al cuadrado;
- es la gravedad definida en el ecuador y los polos, respectivamente;
- (fórmula constante);
entonces, donde , [19]
- .
donde los semiejes de la tierra son:
La diferencia entre la fórmula WGS-84 y la ecuación de Helmert es menor a 0,68 μm·s −2 .
Se aplican reducciones adicionales para obtener anomalías de gravedad (ver: Anomalía de gravedad#Cálculo ).
Estimandogramode la ley de gravitación universal
De la ley de gravitación universal , la fuerza sobre un cuerpo que actúa sobre la fuerza gravitacional de la Tierra está dada por
donde r es la distancia entre el centro de la Tierra y el cuerpo (ver abajo), y aquí tomamos como la masa de la Tierra y m como la masa del cuerpo.
Además, la segunda ley de Newton , F = ma , donde m es masa y a es aceleración, aquí nos dice que
Comparando las dos fórmulas se ve que:
Entonces, para encontrar la aceleración debida a la gravedad al nivel del mar, sustituimos los valores de la constante gravitacional , G , la masa de la Tierra (en kilogramos), m 1 , y el radio de la Tierra (en metros), r , para obtener el valor de g : [20]
Esta fórmula sólo funciona gracias al hecho matemático de que la gravedad de un cuerpo esférico uniforme, medida sobre su superficie o por encima de ella, es la misma que si toda su masa estuviera concentrada en un punto en su centro. Esto es lo que nos permite utilizar el radio de la Tierra para r .
El valor obtenido coincide aproximadamente con el valor medido de g . La diferencia puede atribuirse a varios factores, mencionados anteriormente en "Variación de magnitud":
- La Tierra no es homogénea
- La Tierra no es una esfera perfecta y se debe utilizar un valor promedio para su radio.
- Este valor calculado de g solo incluye la gravedad real. No incluye la reducción de la fuerza restrictiva que percibimos como una reducción de la gravedad debido a la rotación de la Tierra y parte de la gravedad contrarrestada por la fuerza centrífuga.
Existen incertidumbres significativas en los valores de r y m 1 utilizados en este cálculo, y el valor de G también es bastante difícil de medir con precisión.
Si se conocen G , g y r , un cálculo inverso dará una estimación de la masa de la Tierra. Este método fue utilizado por Henry Cavendish .
Medición
La medida de la gravedad de la Tierra se llama gravimetría .
Mediciones satelitales

En la actualidad, los parámetros estáticos y variables en el tiempo del campo gravitatorio de la Tierra se determinan utilizando misiones satelitales modernas, como GOCE , CHAMP , Swarm , GRACE y GRACE-FO . [21] [22] Los parámetros de menor grado, incluida la oblatividad de la Tierra y el movimiento del geocentro, se determinan mejor mediante el alcance láser satelital . [23]
Las anomalías gravitacionales a gran escala pueden detectarse desde el espacio como un subproducto de las misiones de gravedad por satélite, por ejemplo, GOCE . Estas misiones satelitales tienen como objetivo la recuperación de un modelo detallado del campo gravitacional de la Tierra, que se presenta normalmente en forma de una expansión armónica esférica del potencial gravitatorio de la Tierra, pero también se producen presentaciones alternativas, como mapas de ondulaciones geoidales o anomalías gravitacionales.
El Experimento de Recuperación de Gravedad y Clima (GRACE) constaba de dos satélites que detectaban cambios gravitacionales en la Tierra. Estos cambios también podían presentarse como variaciones temporales de anomalías gravitacionales. El Laboratorio de Recuperación de Gravedad e Interior (GRAIL) también constaba de dos naves espaciales que orbitaban la Luna, que estuvieron en órbita durante tres años antes de salir de órbita en 2015.Véase también
- Velocidad de escape : concepto de mecánica celeste
- Escape atmosférico : pérdida de gases atmosféricos planetarios hacia el espacio exterior
- Figura de la Tierra : tamaño y forma utilizados para modelar la Tierra para la geodesia
- Geopotencial : energía relacionada con la gravedad de la Tierra
- Modelo geopotencial : descripción teórica de la forma gravimétrica de la TierraPages displaying short descriptions of redirect targets
- Anomalía de Bouguer – Tipo de anomalía gravitacional
- Gravitación de la Luna
- Aceleración gravitacional : cambio en la velocidad debido únicamente a la gravedad
- Gravedad – Atracción de masas y energía
- Anomalía gravitacional : diferencia entre la aceleración gravitacional ideal y la observada en un lugar
- Gravedad de Marte – Fuerza gravitacional ejercida por el planeta Marte
- Ley de gravitación universal de Newton : enunciado clásico de la gravedad como fuerza
- Desviación vertical : medida del desplazamiento de la fuerza gravitacional hacia abajo debido a la masa cercana.
Referencias
- ^ NASA/JPL/Centro de Investigación Espacial de la Universidad de Texas. "PIA12146: Animación de gravedad global GRACE". Fotodiario . Laboratorio de Propulsión a Chorro de la NASA . Consultado el 30 de diciembre de 2013 .
- ^ ab Boynton, Richard (2001). "Medición precisa de la masa" (PDF) . Documento Sawe n.º 3147. Arlington, Texas: SAWE, Inc. Archivado desde el original (PDF) el 27 de febrero de 2007. Consultado el 22 de diciembre de 2023 .
- ^ Hofmann-Wellenhof, B.; Moritz, H. (2006). Geodesia física (2.ª ed.). Springer. ISBN 978-3-211-33544-4.§ 2.1: "La fuerza total que actúa sobre un cuerpo en reposo sobre la superficie de la Tierra es la resultante de la fuerza gravitatoria y de la fuerza centrífuga de rotación de la Tierra y se llama gravedad".
- ^ Oficina Internacional de Poids et Mesures (1901). "Declaración relativa a la unidad de masa y a la definición de pesos; valor convencional de g n ". Comptes Rendus des Séances de la Troisième Conférence · Générale des Poids et Mesures (en francés). París: Gauthier-Villars. pag. 68.
El nombre adoptado en el Servicio Internacional de Pesos y Medidas para el valor de aceleración normal del pesanteur es 980,665 cm/seg², nombre sancionado déjà por algunas leyes. Declaración relativa a la unidad de masa y a la definición de pesos; valor convencional de
g
n
.
- ^ Moritz, Helmut (2000). "Sistema de referencia geodésica 1980". Journal of Geodesy . 74 (1): 128–133. doi :10.1007/s001900050278. S2CID 195290884 . Consultado el 26 de julio de 2023 .
γe = 9,780 326 7715 m/s² gravedad normal en el ecuador
- ^ Hirt, Christian; Claessens, Sten; Fecher, Thomas; Kuhn, Michael; Pail, Roland; Rexer, Moritz (28 de agosto de 2013). "Nueva imagen de ultraalta resolución del campo gravitatorio de la Tierra". Geophysical Research Letters . 40 (16): 4279–4283. Bibcode :2013GeoRL..40.4279H. doi :10.1002/grl.50838. hdl : 20.500.11937/46786 . S2CID 54867946.
- ^ "Wolfram|Alpha Gravity in Kuala Lumpur", Wolfram Alpha, consultado en noviembre de 2020
- ^ Terry Quinn (2011). De los artefactos a los átomos: el BIPM y la búsqueda de los estándares de medición definitivos . Oxford University Press . pág. 127. ISBN. 978-0-19-530786-3.
- ^ Resolución de la 3.ª CGPM (1901), página 70 (en cm/s 2 ). BIPM – Resolución de la 3.ª CGPM
- ^ "¿Tienes curiosidad por la astronomía?". Universidad de Cornell . Archivado desde el original el 28 de julio de 2013. Consultado el 22 de diciembre de 2023 .
- ^ "Me siento 'más ligero' cuando estoy en la montaña, pero ¿lo estoy?", Preguntas frecuentes del Laboratorio Nacional de Física
- ^ "Las G en la máquina" Archivado el 21 de septiembre de 2020 en Wayback Machine , NASA, consulte "Nota del editor n.° 2"
- ^ ab AM Dziewonski, DL Anderson (1981). "Modelo preliminar de referencia de la Tierra" (PDF) . Física de la Tierra y los interiores planetarios . 25 (4): 297–356. Bibcode :1981PEPI...25..297D. doi :10.1016/0031-9201(81)90046-7. ISSN 0031-9201.
- ^ Tipler, Paul A. (1999). Física para científicos e ingenieros (4.ª ed.). Nueva York: WH Freeman/Worth Publishers. pp. 336–337. ISBN 9781572594913.
- ^ Watts, AB; Daly, SF (mayo de 1981). "Gravedad de longitud de onda larga y anomalías topográficas". Revista anual de ciencias de la Tierra y planetarias . 9 : 415–418. Bibcode :1981AREPS...9..415W. doi :10.1146/annurev.ea.09.050181.002215.
- ^ Widget de campos gravitacionales del 25 de octubre de 2012 – WolframAlpha
- ^ TM Yarwood y F. Castle, Tablas físicas y matemáticas , edición revisada, Macmillan and Co LTD, Londres y Basingstoke, impreso en Gran Bretaña por The University Press, Glasgow, 1970, págs. 22 y 23.
- ^ Fórmula de gravedad internacional Archivado el 20 de agosto de 2008 en Wayback Machine.
- ^ ab "Departamento de Defensa Sistema Geodético Mundial 1984 ― Su Definición y Relaciones con los Sistemas Geodéticos Locales, NIMA TR8350.2, 3ra ed., Tbl. 3.4, Eq. 4-1" (PDF) . Archivado desde el original (PDF) el 2014-04-11 . Consultado el 2015-10-15 .
- ^ "Gravitación". www.ncert.nic . Consultado el 25 de enero de 2022 .
- ^ Meyer, Ulrich; Sosnica, Krzysztof; Arnold, Daniel; Dahle, Christoph; Thaller, Daniela; Dach, Rolf; Jäggi, Adrian (22 de abril de 2019). "Determinación y combinación de campos gravitatorios de enjambre, GRACE y SLR". Teledetección . 11 (8): 956. Bibcode :2019RemS...11..956M. doi : 10.3390/rs11080956 . hdl : 10281/240694 .
- ^ Tapley, Byron D.; Watkins, Michael M.; Flechtner, Frank; Reigber, Christoph; Bettadpur, Srinivas; Rodell, Matthew; Sasgen, Ingo; Famiglietti, James S.; Landerer, Felix W.; Chambers, Don P.; Reager, John T.; Gardner, Alex S.; Save, Himanshu; Ivins, Erik R.; Swenson, Sean C.; Boening, Carmen; Dahle, Christoph; Wiese, David N.; Dobslaw, Henryk; Tamisiea, Mark E.; Velicogna, Isabella (mayo de 2019). "Contribuciones de GRACE a la comprensión del cambio climático". Nature Climate Change . 9 (5): 358–369. Código Bibliográfico :2019NatCC...9..358T. doi :10.1038/s41558-019-0456-2. Número de modelo : PMID 31534490.
- ^ Sośnica, Krzysztof; Jäggi, Adrian; Meyer, Ulrich; Thaller, Daniela; Beutler, Gerhard; Arnold, Daniel; Dach, Rolf (octubre de 2015). "Campo de gravedad de la Tierra variable en el tiempo desde satélites SLR". Journal of Geodesy . 89 (10): 945–960. Código Bibliográfico :2015JGeod..89..945S. doi : 10.1007/s00190-015-0825-1 .
Enlaces externos
- Calculadora de gravedad y altitud
- GRACE – Experimento sobre recuperación de la gravedad y el clima Archivado el 1 de diciembre de 2009 en Wayback Machine
- Datos de alta resolución de GGMplus (2013)
- Modelo Geoid 2011 Potsdam Gravedad Patata









![{\displaystyle g\{\phi \}=\mathbb {G} _{e}\left[{\frac {1+k\sin ^{2}\phi }{\sqrt {1-e^{2} \sin ^{2}\phi }}}\right],\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97407aaf9a74abb8c77b3ec6688ab860e83e96e4)





![{\displaystyle g\{\phi \}=9.7803253359\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\left[{\frac {1+0.001931852652\,\sin ^{2 }\phi }{\sqrt {1-0.0066943799901\,\sin ^{2}\phi }}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f2dc705fdbd2daffda3980f1284916c93351347)







