Paradoja temporal
Paradoja teórica resultante del viaje en el tiempo

Una paradoja temporal , paradoja del tiempo o paradoja del viaje en el tiempo es una paradoja , una aparente contradicción o una contradicción lógica asociada con la idea del viaje en el tiempo u otro conocimiento previo del futuro. Si bien la noción de viajar en el tiempo hacia el futuro cumple con la comprensión actual de la física a través de la dilatación del tiempo relativista , las paradojas temporales surgen de circunstancias que involucran un hipotético viaje en el tiempo hacia el pasado y a menudo se utilizan para demostrar su imposibilidad.

Tipos

Las paradojas temporales se dividen en tres grandes grupos: paradojas de bootstrap, paradojas de consistencia y paradoja de Newcomb. [1] Las paradojas de bootstrap violan la causalidad al permitir que los eventos futuros influyan en el pasado y se causen a sí mismos, o " bootstrapping ", que deriva de la expresión "pull oneself up by one's bootstraps" [2] [3] Las paradojas de consistencia, por otro lado, son aquellas en las que los eventos futuros influyen en el pasado para causar una aparente contradicción, ejemplificada por la paradoja del abuelo , donde una persona viaja al pasado para evitar la concepción de uno de sus antepasados, eliminando así a todos los descendientes del antepasado. [4] La paradoja de Newcomb se deriva de las aparentes contradicciones que surgen de los supuestos tanto del libre albedrío como del conocimiento previo de los eventos futuros. A todas ellas a veces se las denomina individualmente "bucles causales". El término " bucle temporal " a veces se refiere a un bucle causal, [2] pero, aunque parecen similares, los bucles causales son inmutables y se originan por sí mismos, mientras que los bucles temporales se reinician constantemente. [5]

Paradoja del bootstrap

Una paradoja de arranque, también conocida como bucle de información , paradoja de la información , [6] paradoja ontológica , [7] o "paradoja de la predestinación", es una paradoja del viaje en el tiempo que ocurre cuando cualquier evento, como una acción, información, un objeto o una persona, en última instancia se causa a sí mismo, como consecuencia de la retrocausalidad o del viaje en el tiempo . [8] [9] [10] [11]

Los viajes en el tiempo hacia atrás permitirían que la información, las personas o los objetos cuyas historias parecen "venir de la nada". [8] Tales eventos causalmente enlazados existen entonces en el espacio-tiempo , pero su origen no puede determinarse. [8] [9] La noción de objetos o información que son "autoexistentes" de esta manera a menudo se considera paradójica. [9] [6] [12] Everett da la película Somewhere in Time como un ejemplo que involucra un objeto sin origen: una anciana le da un reloj a un dramaturgo que luego viaja en el tiempo y conoce a la misma mujer cuando era joven, y le da el mismo reloj que ella más tarde le dará a él. [6] Un ejemplo de información que "vino de la nada" está en la película Star Trek IV: The Voyage Home , en la que un ingeniero del siglo XXIII viaja en el tiempo y le da la fórmula del aluminio transparente al ingeniero del siglo XX que supuestamente lo inventó.

Paradoja de la predestinación

Smeenk utiliza el término "paradoja de la predestinación" para referirse específicamente a situaciones en las que un viajero en el tiempo retrocede en el tiempo para intentar evitar algún acontecimiento del pasado. [7]

Paradoja del abuelo

La paradoja de la consistencia o paradoja del abuelo ocurre cuando el pasado se modifica de alguna manera, creando así una contradicción. Un ejemplo común dado es viajar al pasado e intervenir en la concepción de los antepasados ​​de uno (como causar la muerte del padre de antemano), afectando así la concepción de uno mismo. Si el viajero en el tiempo no hubiera nacido, entonces no sería posible que el viajero llevara a cabo tal acto en primer lugar. Por lo tanto, el antepasado vive para descendencia del antepasado de la siguiente generación del viajero en el tiempo, y eventualmente del viajero en el tiempo. Por lo tanto, no hay un resultado previsto para esto. [8] Las paradojas de la consistencia ocurren siempre que sea posible cambiar el pasado. [9] Una posible resolución es que un viajero en el tiempo puede hacer cualquier cosa que sucedió , pero no puede hacer nada que no sucedió. Hacer algo que no sucedió da como resultado una contradicción. [8] Esto se conoce como el principio de autoconsistencia de Novikov .

Variantes

La paradoja del abuelo abarca cualquier cambio en el pasado, [13] y se presenta en muchas variaciones, incluyendo el asesinato del yo pasado. [14] [15] Tanto la "paradoja del retro-suicidio" como la "paradoja del abuelo" aparecieron en cartas escritas en Amazing Stories en la década de 1920. [16] Otra variante de la paradoja del abuelo es la "paradoja de Hitler" o "paradoja del asesinato de Hitler", en la que el protagonista viaja en el tiempo para asesinar a Adolf Hitler antes de que pueda instigar la Segunda Guerra Mundial y el Holocausto . En lugar de impedir físicamente el viaje en el tiempo, la acción elimina cualquier razón para el viaje, junto con cualquier conocimiento de que la razón alguna vez existió. [17]

El físico John Garrison y otros ofrecen una variación de la paradoja de un circuito electrónico que envía una señal a través de una máquina del tiempo para apagarse y recibe la señal antes de enviarla. [18] [19]

La paradoja de Newcomb

La paradoja de Newcomb es un experimento mental que muestra una aparente contradicción entre el principio de utilidad esperada y el principio de dominio estratégico . [20] El experimento mental se extiende a menudo para explorar la causalidad y el libre albedrío al permitir "predictores perfectos": si existen predictores perfectos del futuro, por ejemplo, si el viaje en el tiempo existe como un mecanismo para hacer predicciones perfectas [ ¿cómo? ] , entonces las predicciones perfectas parecen contradecir el libre albedrío porque las decisiones aparentemente tomadas con libre albedrío ya son conocidas por el predictor perfecto [ aclaración necesaria ] . [21] [22] La predestinación no implica necesariamente un poder sobrenatural , y podría ser el resultado de otros mecanismos de "conocimiento previo infalible". [23] Los problemas que surgen de la infalibilidad y que influyen en el futuro se exploran en la paradoja de Newcomb. [24]

Resoluciones propuestas

Imposibilidad lógica

Incluso sin saber si viajar en el tiempo al pasado es físicamente posible, es posible demostrar mediante la lógica modal que cambiar el pasado da como resultado una contradicción lógica. Si es necesariamente cierto que el pasado ocurrió de una determinada manera, entonces es falso e imposible que el pasado haya ocurrido de otra manera. Un viajero en el tiempo no podría cambiar el pasado de la forma en que es , sino que solo actuaría de una manera que ya es consistente con lo que necesariamente ocurrió. [25] [26]

La consideración de la paradoja del abuelo ha llevado a algunos a la idea de que el viaje en el tiempo es por su propia naturaleza paradójico y, por lo tanto, lógicamente imposible. Por ejemplo, el filósofo Bradley Dowden formuló este tipo de argumento en el libro de texto Razonamiento lógico , argumentando que la posibilidad de crear una contradicción descarta por completo el viaje en el tiempo al pasado. Sin embargo, algunos filósofos y científicos creen que el viaje en el tiempo al pasado no tiene por qué ser lógicamente imposible siempre que no haya posibilidad de cambiar el pasado, [13] como lo sugiere, por ejemplo, el principio de autoconsistencia de Novikov . Dowden revisó su punto de vista después de convencerse de esto en un intercambio con el filósofo Norman Swartz . [27]

Tiempo ilusorio

La consideración de la posibilidad de un viaje en el tiempo hacia atrás en un universo hipotético descrito por una métrica de Gödel llevó al famoso lógico Kurt Gödel a afirmar que el tiempo en sí mismo podría ser una especie de ilusión. [28] [29] Él sugiere algo parecido a la visión del tiempo en bloques , en la que el tiempo es simplemente otra dimensión como el espacio, con todos los eventos en todo momento fijados dentro de este "bloque" de cuatro dimensiones. [ cita requerida ]

Imposibilidad física

Sergey Krasnikov escribe que estas paradojas de arranque (información o un objeto que se mueve en bucle a través del tiempo) son las mismas; la aparente paradoja primaria es un sistema físico que evoluciona hacia un estado de una manera que no está gobernada por sus leyes. [30] : 4  No las encuentra paradójicas y atribuye los problemas relacionados con la validez del viaje en el tiempo a otros factores en la interpretación de la relatividad general. [30] : 14–16 

Bucles autosuficientes

Un artículo de 1992 de los físicos Andrei Lossev e Igor Novikov etiquetó a estos objetos sin origen como Jinn , con el término singular Jinnee . [31] : 2311–2312  Esta terminología se inspiró en los Jinn del Corán , que se describe que no dejan rastro cuando desaparecen. [32] : 200–203  Lossev y Novikov permitieron que el término "Jinn" cubriera tanto objetos como información con el origen reflexivo; llamaron a los primeros "Jinn del primer tipo", y a los segundos "Jinn del segundo tipo". [6] [31] : 2315–2317  [32] : 208  Señalan que un objeto que hace un paso circular a través del tiempo debe ser idéntico siempre que se lo traiga de regreso al pasado, de lo contrario crearía una inconsistencia; La segunda ley de la termodinámica parece requerir que el objeto tienda a un estado de energía más bajo a lo largo de su historia, y los objetos que son idénticos en puntos repetidos en su historia parecen contradecir esto, pero Lossev y Novikov argumentaron que, dado que la segunda ley solo requiere que la entropía aumente en sistemas cerrados , un Jinnee podría interactuar con su entorno de tal manera que recupere la entropía "perdida". [6] [32] : 200–203  Destacan que no hay una "diferencia estricta" entre Jinn de primer y segundo tipo. [31] : 2320  Krasnikov hace una distinción equivocada entre "Jinn", "bucles autosuficientes" y "objetos autoexistentes", llamándolos "leones" u "objetos en bucle o intrusos", y afirma que no son menos físicos que los objetos convencionales, "que, después de todo, también podrían aparecer solo desde el infinito o una singularidad". [30] : 8–9 

Principio de autoconsistencia de Novikov

El principio de autoconsistencia desarrollado por Igor Dmitriyevich Novikov [33] : p. 42 nota 10  expresa una visión de cómo sería posible el viaje en el tiempo hacia atrás sin la generación de paradojas. Según esta hipótesis, aunque la relatividad general permite algunas soluciones exactas que permiten el viaje en el tiempo [34] que contienen curvas temporales cerradas que conducen de vuelta al mismo punto en el espacio-tiempo, [35] la física en o cerca de curvas temporales cerradas (máquinas del tiempo) solo puede ser consistente con las leyes universales de la física, y por lo tanto solo pueden ocurrir eventos autoconsistentes. Cualquier cosa que un viajero en el tiempo haga en el pasado debe haber sido parte de la historia desde el principio, y el viajero en el tiempo nunca puede hacer nada para evitar que ocurra el viaje en el tiempo, ya que esto representaría una inconsistencia. Los autores concluyeron que el viaje en el tiempo no necesariamente conduce a paradojas irresolubles, independientemente del tipo de objeto que se haya enviado al pasado. [36]

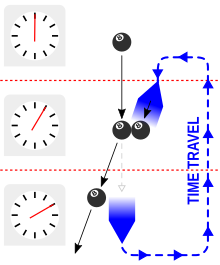
Arriba: trayectoria original de la bola de billar. En medio: la bola de billar emerge del futuro y le asesta a su yo del pasado un golpe que evita que la bola del pasado entre en la máquina del tiempo. Abajo: la bola de billar nunca entra en la máquina del tiempo, lo que da lugar a la paradoja, que pone en tela de juicio cómo su yo anterior podría emerger de la máquina del tiempo y desviar su curso.

El físico Joseph Polchinski consideró una situación potencialmente paradójica que involucraba una bola de billar que se lanzaba a un agujero de gusano en el ángulo justo para que fuera enviada hacia atrás en el tiempo y colisionara con su yo anterior, sacándola de su curso, lo que le impediría entrar en el agujero de gusano en primer lugar. Kip Thorne se refirió a este problema como "la paradoja de Polchinski". [36] Thorne y dos de sus estudiantes en Caltech, Fernando Echeverría y Gunnar Klinkhammer, continuaron para encontrar una solución que evitaba cualquier inconsistencia, y descubrieron que había más de una solución autoconsistente, con ángulos ligeramente diferentes para el golpe de refilón en cada caso. [37] Un análisis posterior de Thorne y Robert Forward mostró que para ciertas trayectorias iniciales de la bola de billar, podría haber un número infinito de soluciones autoconsistentes. [36] Es plausible que existan extensiones autoconsistentes para cada posible trayectoria inicial, aunque esto no ha sido probado. [38] : 184  La falta de restricciones en las condiciones iniciales sólo se aplica al espacio-tiempo fuera de la región del espacio-tiempo que viola la cronología ; las restricciones en la región que viola la cronología podrían resultar paradójicas, pero esto aún no se sabe. [38] : 187–188 

Las opiniones de Novikov no son ampliamente aceptadas. Visser considera los bucles causales y el principio de autoconsistencia de Novikov como una solución ad hoc , y supone que existen implicaciones mucho más dañinas del viaje en el tiempo. [39] Krasnikov, de manera similar, no encuentra fallas inherentes en los bucles causales, pero encuentra otros problemas con el viaje en el tiempo en la relatividad general. [30] : 14–16  Otra conjetura, la hipótesis de la censura cósmica , sugiere que cada curva temporal cerrada pasa a través de un horizonte de eventos , lo que impide que se observen tales bucles causales. [40]

Universos paralelos

El enfoque de múltiples universos interactuantes es una variación de la interpretación de muchos mundos de la mecánica cuántica que implica que los viajeros en el tiempo llegan a un universo diferente de aquel del que vinieron; se ha argumentado que, dado que los viajeros llegan a la historia de un universo diferente y no a su historia, esto no es un viaje en el tiempo "genuino". [41] Stephen Hawking ha defendido la conjetura de protección de la cronología , que incluso si la MWI es correcta, deberíamos esperar que cada viajero en el tiempo experimente una única historia autoconsistente para que los viajeros en el tiempo permanezcan dentro de su mundo en lugar de viajar a uno diferente. [42]

David Deutsch ha propuesto que la computación cuántica con un retraso negativo (viaje en el tiempo hacia atrás) produce solo soluciones autoconsistentes, y la región que viola la cronología impone restricciones que no son evidentes a través del razonamiento clásico. [43] Sin embargo, se ha demostrado que la condición de autoconsistencia de Deutsch puede cumplirse con precisión arbitraria por cualquier sistema sujeto a las leyes de la mecánica estadística clásica , incluso si no está construida por sistemas cuánticos. [44] Allen Everett también ha argumentado que incluso si el enfoque de Deutsch es correcto, implicaría que cualquier objeto macroscópico compuesto de múltiples partículas se dividiría al viajar hacia atrás en el tiempo, y que diferentes partículas emergerían en mundos diferentes. [45]

Véase también

Referencias

  1. ^ Jan Faye (18 de noviembre de 2015), "Backward Causation", Stanford Encyclopedia of Philosophy , consultado el 25 de mayo de 2019
  2. ^ ab Klosterman, Chuck (2009). Eating the Dinosaur (1.ª edición de tapa dura de Scribner). Nueva York: Scribner. pp. 60–62. ISBN 9781439168486.
  3. ^ Ross, Kelley L. (1997). "Paradojas del viaje en el tiempo". Archivado desde el original el 18 de enero de 1998.
  4. ^ Francisco Lobo (2003). "Tiempo, curvas temporales cerradas y causalidad". Nato Science Series II . 95 : 289–296. arXiv : gr-qc/0206078 . Código Bibliográfico :2003ntgp.conf..289L.
  5. ^ Jones, Matthew; Ormrod, Joan (2015). Viajes en el tiempo en los medios populares . McFarland & Company . pág. 207. ISBN. 9780786478071.
  6. ^ abcde Everett, Allen; Roman, Thomas (2012). Viajes en el tiempo y motores de curvatura . Chicago: University of Chicago Press. págs. 136-139. ISBN. 978-0-226-22498-5.
  7. ^ ab Smeenk, Chris; Wüthrich, Christian (2011), "Viajes en el tiempo y máquinas del tiempo", en Callender, Craig (ed.), The Oxford Handbook of Philosophy of Time , Oxford University Press, pág. 581, ISBN 978-0-19-929820-4
  8. ^ abcde Smith, Nicholas JJ (2013). "Viajes en el tiempo". Stanford Encyclopedia of Philosophy . Consultado el 13 de junio de 2015 .
  9. ^ abcd Lobo, Francisco (2003). "Tiempo, curvas temporales cerradas y causalidad". La naturaleza del tiempo: geometría, física y percepción . NATO Science Series II. Vol. 95. págs. 289–296. arXiv : gr-qc/0206078 . Código Bibliográfico :2003ntgp.conf..289L. ISBN. 1-4020-1200-4.
  10. ^ Rea, Michael (2014). Metafísica: Fundamentos (1.ª ed. publ.). Nueva York: Routledge. p. 78. ISBN 978-0-415-57441-9.
  11. ^ Rea, Michael C. (2009). Argumentando sobre metafísica . Nueva York [ua]: Routledge. p. 204. ISBN 978-0-415-95826-4.
  12. ^ Visser, Matt (1996). Agujeros de gusano lorentzianos: de Einstein a Hawking . Nueva York: Springer-Verlag. pág. 213. ISBN. 1-56396-653-0.
  13. ^ de Nicholas JJ Smith (2013). "Viajes en el tiempo". Stanford Encyclopedia of Philosophy . Consultado el 2 de noviembre de 2015 .
  14. ^ Horwich, Paul (1987). Asimetrías en el tiempo: problemas en la filosofía de la ciencia (2.ª ed.). Cambridge, Massachusetts: MIT Press. p. 116. ISBN 0262580888.
  15. ^ Jan Faye (18 de noviembre de 2015), "Backward Causation", Stanford Encyclopedia of Philosophy , consultado el 25 de mayo de 2019
  16. ^ Nahin, Paul J. (1999). Máquinas del tiempo: viajes en el tiempo en física, metafísica y ciencia ficción (2.ª ed.). Nueva York: Springer-Verlag. ISBN 0-387-98571-9. Recuperado el 19 de febrero de 2022 .
  17. ^ Brennan, JH (1997). Viajes en el tiempo: una nueva perspectiva (1.ª ed.). Minnesota: Llewellyn Publications. pág. 23. ISBN 9781567180855.
  18. ^ Garrison, JC; Mitchell, MW; Chiao, RY; Bolda, EL (agosto de 1998). "Señales superlumínicas: paradojas de bucles causales revisitadas". Physics Letters A . 245 (1–2): 19–25. arXiv : quant-ph/9810031 . Código Bibliográfico :1998PhLA..245...19G. doi :10.1016/S0375-9601(98)00381-8. S2CID  51796022.
  19. ^ Nahin, Paul J. (2016). Cuentos de la máquina del tiempo . Springer International Publishing. págs. 335–336. ISBN 9783319488622.
  20. ^ Wolpert, DH; Benford, G. (junio de 2013). "La lección de la paradoja de Newcomb". Síntesis . 190 (9): 1637–1646. doi :10.1007/s11229-011-9899-3. JSTOR  41931515. S2CID  113227.
  21. ^ Craig (1987). "Presciencia divina y paradoja de Newcomb". Philosophia . 17 (3): 331–350. doi :10.1007/BF02455055. S2CID  143485859.
  22. ^ Craig, William Lane (1988). "Taquiones, viajes en el tiempo y omnisciencia divina". Revista de Filosofía . 85 (3): 135–150. doi :10.2307/2027068. JSTOR  2027068.
  23. ^ Craig, William Lane (1987). "La presciencia divina y la paradoja de Newcomb". Philosophia . 17 (3): 331–350. doi :10.1007/BF02455055. S2CID  143485859.
  24. ^ Dummett, Michael (1996). Los mares del lenguaje . Oxford University Press. pp. 356, 370–375. ISBN 9780198240112.
  25. ^ Norman Swartz (2001), Más allá de la experiencia: teorías metafísicas y restricciones filosóficas, University of Toronto Press, págs. 226-227
  26. ^ Dummett, Michael (1996). Los mares del lenguaje (Nueva edición). Oxford: Oxford University Press. pp. 368–369. ISBN 0198236212.
  27. ^ Norman Swartz (1993). "Viajes en el tiempo: una visita al pasado". SFU.ca. Consultado el 21 de abril de 2016 .
  28. ^ Yourgrau, Palle (4 de marzo de 2009). Un mundo sin tiempo: el legado olvidado de Gödel y Einstein. Nueva York: Basic Books. pág. 134. ISBN 9780786737000. Recuperado el 18 de diciembre de 2017 .
  29. ^ Holt, Jim (21 de febrero de 2005). "Time Bandits". The New Yorker . Consultado el 13 de diciembre de 2017 .
  30. ^ abcd Krasnikov, S. (2001), "La paradoja del viaje en el tiempo", Phys. Rev. D , 65 (6): 06401, arXiv : gr-qc/0109029 , Bibcode :2002PhRvD..65f4013K, doi :10.1103/PhysRevD.65.064013, S2CID  18460829
  31. ^ abc Lossev, Andrei; Novikov, Igor (15 de mayo de 1992). "Los genios de la máquina del tiempo: soluciones autoconsistentes no triviales" (PDF) . Clase. Gravedad cuántica . 9 (10): 2309–2321. Código Bibliográfico :1992CQGra...9.2309L. doi :10.1088/0264-9381/9/10/014. S2CID  250912686. Archivado desde el original (PDF) el 17 de noviembre de 2015 . Consultado el 16 de noviembre de 2015 .
  32. ^ abc Toomey, David (2012). Los nuevos viajeros del tiempo. Nueva York, Nueva York: WW Norton & Company. ISBN 978-0-393-06013-3.
  33. ^ Friedman, John; Morris, Michael S.; Novikov, Igor D.; Echeverría, Fernando; Klinkhammer, Gunnar; Thorne, Kip S.; Yurtsever, Ulvi (1990). "Problema de Cauchy en espacio-tiempos con curvas temporales cerradas". Physical Review D . 42 (6): 1915–1930. Bibcode :1990PhRvD..42.1915F. doi :10.1103/PhysRevD.42.1915. PMID  10013039.
  34. ^ Krasnikov, S. (2002), "No hay máquinas del tiempo en la relatividad general clásica", Gravedad clásica y cuántica , 19 (15): 4109, arXiv : gr-qc/0111054 , Bibcode :2002CQGra..19.4109K, doi :10.1088/0264-9381/19/15/316, S2CID  16517920
  35. ^ Gödel, Kurt (1949). "Un ejemplo de un nuevo tipo de solución cosmológica de las ecuaciones de campo de gravitación de Einstein". Rev. Mod. Phys . 21 (3): 447–450. Bibcode :1949RvMP...21..447G. doi : 10.1103/RevModPhys.21.447 .
  36. ^ abc Thorne, Kip S. (1994). Agujeros negros y distorsiones temporales . WW Norton. págs. 509–513. ISBN 0-393-31276-3.
  37. ^ Echeverría, Fernando; Gunnar Klinkhammer; Kip Thorne (1991). "Bolas de billar en espacios-tiempos de agujeros de gusano con curvas temporales cerradas: teoría clásica". Physical Review D . 44 (4): 1077–1099. Bibcode :1991PhRvD..44.1077E. doi :10.1103/PhysRevD.44.1077. PMID  10013968.
  38. ^ ab Earman, John (1995). Golpes, crujidos, gemidos y chillidos: singularidades y acausalidades en los espacio-tiempos relativistas . Oxford University Press. ISBN 0-19-509591-X.
  39. ^ Nahin, Paul J. (1999). Máquinas del tiempo: viajes en el tiempo en física, metafísica y ciencia ficción . Instituto Americano de Física. pp. 345–352. ISBN. 0-387-98571-9.
  40. ^ Visser, Matt (15 de abril de 1997). "Agujeros de gusano atravesables: el anillo romano". Physical Review D . 55 (8): 5212–5214. arXiv : gr-qc/9702043 . Código Bibliográfico :1997PhRvD..55.5212V. doi :10.1103/PhysRevD.55.5212. S2CID  2869291.
  41. ^ Frank Arntzenius; Tim Maudlin (23 de diciembre de 2009), "Viajes en el tiempo y física moderna", Stanford Encyclopedia of Philosophy , consultado el 25 de mayo de 2019
  42. ^ Hawking, Stephen (1999). «Deformaciones del espacio y del tiempo». Archivado desde el original el 10 de febrero de 2012. Consultado el 25 de febrero de 2012 .
  43. ^ Deutsch, David (15 de noviembre de 1991). "Mecánica cuántica cerca de líneas temporales cerradas". Physical Review D . 44 (10): 3197–3217. Bibcode :1991PhRvD..44.3197D. doi :10.1103/PhysRevD.44.3197. PMID  10013776.
  44. ^ Tolksdorf, Juergen; Verch, Rainer (2021). "La condición D-CTC se cumple genéricamente en sistemas estadísticos clásicos (no cuánticos)". Fundamentos de la física . 51 (93): 93. arXiv : 1912.02301 . Código Bibliográfico :2021FoPh...51...93T. doi :10.1007/s10701-021-00496-z. S2CID  208637445.
  45. ^ Everett, Allen (2004). "Paradojas del viaje en el tiempo, integrales de trayectoria y la interpretación de los muchos mundos de la mecánica cuántica". Physical Review D . 69 (124023): 124023. arXiv : gr-qc/0410035 . Código Bibliográfico :2004PhRvD..69l4023E. doi :10.1103/PhysRevD.69.124023. S2CID  18597824.
Obtenido de "https://es.wikipedia.org/w/index.php?title=Paradoja_temporal&oldid=1251315741#Bucle_causal"