Relación antisimétrica

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Antisymmetric relation" – news · newspapers · books · scholar · JSTOR (January 2010) (Learn how and when to remove this message)

Relaciones binarias transitivas en a mi
Simétrico Antisimétrico Conectado Bien fundado Tiene uniones Tiene cumple Reflexivo Irreflexivo Asimétrico Total, Semiconnex Anti- reflexivo Relación de equivalencia Y ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Pedido anticipado (cuasi pedido) ✗ ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Orden parcial ✗ Y ✗ ✗ ✗ ✗ Y ✗ ✗ Pedido anticipado total ✗ ✗ Y ✗ ✗ ✗ Y ✗ ✗ Pedido total ✗ Y Y ✗ ✗ ✗ Y ✗ ✗ Preordenamiento de pozos ✗ ✗ Y Y ✗ ✗ Y ✗ ✗ Bien-cuasi-ordenamiento ✗ ✗ ✗ Y ✗ ✗ Y ✗ ✗ Buen orden ✗ Y Y Y ✗ ✗ Y ✗ ✗ Enrejado ✗ Y ✗ ✗ Y Y Y ✗ ✗ Unión de semirrejilla ✗ Y ✗ ✗ Y ✗ Y ✗ ✗ Conocer-semilattice ✗ Y ✗ ✗ ✗ Y Y ✗ ✗ Orden parcial estricta ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Orden débil estricta ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Orden total estricta ✗ Y Y ✗ ✗ ✗ ✗ Y Y Simétrico Antisimétrico Conectado Bien fundado Tiene uniones Tiene cumple Reflexivo Irreflexivo Asimétrico Definiciones, para todos y${\displaystyle a,b}$${\displaystyle S\neq \varnothing :}$ ${\displaystyle {\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}aRb{\text{ and }}&bRa\\\Rightarrow a={}&b\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ or }}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}\min S\\{\text{exists}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\vee b\\{\text{exists}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\wedge b\\{\text{exists}}\end{aligned}}}$ ${\displaystyle aRa}$ ${\displaystyle {\text{not }}aRa}$ ${\displaystyle {\begin{aligned}aRb\Rightarrow \\{\text{not }}bRa\end{aligned}}}$
Yindica que la propiedad de la columna siempre es verdadera para el término de la fila (a la izquierda), mientras que ✗ indica que la propiedad no está garantizada en general (puede cumplirse o no). Por ejemplo, que toda relación de equivalencia es simétrica, pero no necesariamente antisimétrica, se indica con en la columna "Simétrica" ​​y ✗ en la columna "Antisimétrica", respectivamente.Y Todas las definiciones requieren tácitamente que la relación homogénea sea transitiva : para todo si y entonces La definición de un término puede requerir propiedades adicionales que no están incluidas en esta tabla.${\displaystyle R}$${\displaystyle a,b,c,}$${\displaystyle aRb}$${\displaystyle bRc}$${\displaystyle aRc.}$

En matemáticas , una relación binaria en un conjunto es antisimétrica si no hay ningún par de elementos distintos de cada uno de los cuales esté relacionado por con el otro. Más formalmente, es antisimétrica precisamente si para todos o equivalentemente, La definición de antisimetría no dice nada sobre si realmente se cumple o no para cualquier . Una relación antisimétrica en un conjunto puede ser reflexiva (es decir, para todos ), irreflexiva (es decir, para ningún ), o ni reflexiva ni irreflexiva. Una relación es asimétrica si y solo si es antisimétrica e irreflexiva.${\displaystyle R}$ ${\displaystyle X}$${\displaystyle X}$${\displaystyle R}$${\displaystyle R}$${\displaystyle a,b\in X,}$$${\displaystyle {\text{if }}\,aRb\,{\text{ with }}\,a\neq b\,{\text{ then }}\,bRa\,{\text{ must not hold}},}$$$${\displaystyle {\text{if }}\,aRb\,{\text{ and }}\,bRa\,{\text{ then }}\,a=b.}$$${\displaystyle aRa}$${\displaystyle a}$${\displaystyle R}$${\displaystyle X}$${\displaystyle aRa}$${\displaystyle a\in X}$${\displaystyle aRa}$${\displaystyle a\in X}$

La relación de divisibilidad de los números naturales es un ejemplo importante de una relación antisimétrica. En este contexto, antisimetría significa que la única forma en que cada uno de dos números puede ser divisible por el otro es si los dos son, de hecho, el mismo número; equivalentemente, si y son distintos y es un factor de entonces no puede ser un factor de Por ejemplo, 12 es divisible por 4, pero 4 no es divisible por 12.${\displaystyle n}$${\displaystyle m}$${\displaystyle n}$${\displaystyle m,}$${\displaystyle m}$${\displaystyle n.}$

La relación de orden habitual en los números reales es antisimétrica: si para dos números reales y se cumplen ambas desigualdades y , entonces y deben ser iguales. De manera similar, el orden de subconjuntos en los subconjuntos de cualquier conjunto dado es antisimétrico: dados dos conjuntos y si cada elemento en también está en y cada elemento en también está en entonces y deben contener todos los mismos elementos y, por lo tanto, ser iguales: Un ejemplo de la vida real de una relación que es típicamente antisimétrica es "pagó la cuenta del restaurante de" (entendida como restringida a una ocasión dada). Por lo general, algunas personas pagan sus propias cuentas, mientras que otras pagan las de sus cónyuges o amigos. Mientras no haya dos personas que paguen las cuentas entre sí, la relación es antisimétrica.${\displaystyle \,\leq \,}$${\displaystyle x}$${\displaystyle y}$ ${\displaystyle x\leq y}$${\displaystyle y\leq x}$${\displaystyle x}$${\displaystyle y}$ ${\displaystyle \,\subseteq \,}$${\displaystyle A}$${\displaystyle B,}$${\displaystyle A}$${\displaystyle B}$${\displaystyle B}$${\displaystyle A,}$${\displaystyle A}$${\displaystyle B}$$${\displaystyle A\subseteq B{\text{ and }}B\subseteq A{\text{ implies }}A=B}$$

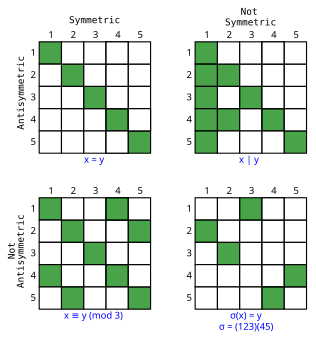
Los órdenes parciales y totales son antisimétricos por definición. Una relación puede ser tanto simétrica como antisimétrica (en este caso, debe ser correflexiva ), y hay relaciones que no son ni simétricas ni antisimétricas (por ejemplo, la relación "se aprovecha de" en especies biológicas ).

La antisimetría es diferente de la asimetría : una relación es asimétrica si y sólo si es antisimétrica e irreflexiva .

• Relación reflexiva  : Relación binaria que relaciona cada elemento consigo mismo.
• Simetría en matemáticas

• Weisstein, Eric W. "Relación antisimétrica". MathWorld .
• Lipschutz, Seymour ; Marc Lars Lipson (1997). Teoría y problemas de las matemáticas discretas . McGraw-Hill. pág. 33. ISBN 0-07-038045-7.
• Relación antisimétrica nLab