Cabezal hidráulico

Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes ) Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes .Por favor, ayude a mejorar este artículo introduciendo citas más precisas. ( Abril de 2020 )( Aprenda cómo y cuándo eliminar este mensaje ) La sección introductoria de este artículo puede ser demasiado breve para resumir adecuadamente los puntos clave .Considere ampliar la introducción para proporcionar una descripción general accesible de todos los aspectos importantes del artículo. ( Octubre de 2024 ) ( Aprenda cómo y cuándo eliminar este mensaje )

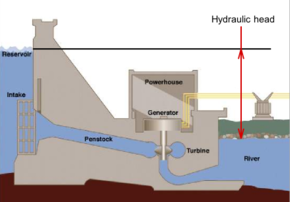
La altura hidráulica o altura piezométrica es una medida específica de la presión del líquido por encima de un punto de referencia vertical . ^{[1] [2]}

Generalmente se mide como una elevación de la superficie del líquido, expresada en unidades de longitud, en la entrada (o fondo) de un piezómetro . En un acuífero , se puede calcular a partir de la profundidad del agua en un pozo piezométrico (un pozo de agua especializado ) y dada la información de la elevación del piezómetro y la profundidad de la pantalla. La carga hidráulica se puede medir de manera similar en una columna de agua utilizando un piezómetro de tubo vertical midiendo la altura de la superficie del agua en el tubo en relación con un dato común. La carga hidráulica se puede utilizar para determinar un gradiente hidráulico entre dos o más puntos.

En dinámica de fluidos , la altura es un concepto que relaciona la energía en un fluido incompresible con la altura de una columna estática equivalente de ese fluido. Según el principio de Bernoulli , la energía total en un punto dado de un fluido es la energía cinética asociada con la velocidad de flujo del fluido, más la energía de la presión estática en el fluido, más la energía de la altura del fluido en relación con un dato arbitrario . ^[3] La altura se expresa en unidades de distancia, como metros o pies. La fuerza por unidad de volumen sobre un fluido en un campo gravitacional es igual a ρg , donde ρ es la densidad del fluido y g es la aceleración gravitacional . En la Tierra, la altura adicional del agua dulce agrega una presión estática de aproximadamente 9,8 kPa por metro (0,098 bar/m) o 0,433 psi por pie de altura de columna de agua.

La altura estática de una bomba es la altura máxima (presión) que puede suministrar. La capacidad de la bomba a una determinada RPM se puede leer en su curva QH (caudal vs. altura).

La altura es útil para especificar bombas centrífugas porque sus características de bombeo tienden a ser independientes de la densidad del fluido.

Generalmente existen cuatro tipos de cabeza:

1. La carga de velocidad se debe al movimiento en masa ( energía cinética ) de un fluido.Nótese quees igual a la presión dinámica para el flujo irrotacional .$${\displaystyle h_{v}={\tfrac {1}{2}}\rho v^{2}/\rho g={\frac {1}{2}}{\frac {v^{2}} {gramo}}}$$${\displaystyle \rho gh_{v}}$
2. La altura de elevación se debe al peso del fluido, la fuerza gravitacional que actúa sobre una columna de fluido. La altura de elevación es simplemente la altura ( h ) del fluido por encima de un punto cero designado arbitrariamente:$${\displaystyle h_{e}=\rho gh/\rho g}$$
3. La carga de presión se debe a la presión estática , el movimiento molecular interno de un fluido que ejerce una fuerza sobre el recipiente que lo contiene. Es igual a la presión dividida por la fuerza/volumen del fluido en un campo gravitacional:$${\displaystyle h_{p}=p/\rho g}$$
4. La carga de resistencia (o carga de fricción o pérdida de carga) se debe a las fuerzas de fricción que actúan contra el movimiento de un fluido por el recipiente. Para un medio continuo, esto se describe mediante la ley de Darcy , que relaciona el caudal volumétrico ( q ) con el gradiente de la carga hidráulica a través de la conductividad hidráulica K : mientras que en un sistema de tuberías las pérdidas de carga se describen mediante la ecuación de Hagen-Poiseuille y la ecuación de Bernoulli .$${\displaystyle \mathbf {q} =-K\nabla h}$$

Después de caer libremente a una cierta altura en el vacío desde una velocidad inicial de 0, una masa habrá alcanzado una velocidad donde es la aceleración debida a la gravedad. Reordenada como cabeza :${\estilo de visualización h}$$${\displaystyle v={\sqrt {{2g}{h}}}}$$${\estilo de visualización g}$$${\displaystyle h={\frac {v^{2}}{2g}}.}$$

El término se denomina carga de velocidad y se expresa como una medida de longitud. En un fluido en movimiento, representa la energía del fluido debido a su movimiento en masa.${\displaystyle {\frac {v^{2}}{2g}}}$

La altura hidráulica total de un fluido se compone de la altura de presión y la altura de elevación . ^{[1] [2] La altura de presión es la} presión manométrica equivalente de una columna de agua en la base del piezómetro, y la altura de elevación es la energía potencial relativa en términos de una elevación. La ecuación de la altura , una forma simplificada del principio de Bernoulli para fluidos incompresibles, se puede expresar como: donde$${\displaystyle h=\psi+z}$$

• ${\estilo de visualización h}$es la altura hidráulica ( longitud en m o ft), también conocida como altura piezométrica.
• ${\estilo de visualización \psi}$es la carga de presión , en términos de la diferencia de elevación de la columna de agua con respecto al fondo del piezómetro ( longitud en m o pies), y
• ${\estilo de visualización z}$es la elevación en la parte inferior del piezómetro ( longitud en m o pies)

En un ejemplo con un piezómetro de 400 m de profundidad, con una elevación de 1000 m y una profundidad al agua de 100 m: z = 600 m, ψ = 300 m y h = 900 m.

La carga de presión se puede expresar como: donde es la presión manométrica (fuerza por unidad de área, a menudo Pa o psi),$${\displaystyle \psi ={\frac {P}{\gamma }}={\frac {P}{\rho g}}}$$${\estilo de visualización P}$

• ${\estilo de visualización \gamma}$es el peso unitario del líquido (fuerza por unidad de volumen, normalmente N·m ⁻³ o lbf /ft ³ ),
• ${\estilo de visualización \rho}$es la densidad del líquido (masa por unidad de volumen, frecuentemente kg·m ⁻³ ), y
• ${\estilo de visualización g}$es la aceleración gravitacional (cambio de velocidad por unidad de tiempo, a menudo m·s ⁻² )

La altura de presión depende de la densidad del agua, que puede variar en función de la temperatura y de la composición química ( en particular, de la salinidad ). Esto significa que el cálculo de la altura hidráulica depende de la densidad del agua dentro del piezómetro. Si se deben comparar una o más mediciones de altura hidráulica, es necesario estandarizarlas, generalmente con respecto a su altura en agua dulce , que se puede calcular como:

$${\displaystyle h_{\mathrm {fw} }=\psi {\frac {\rho }{\rho _{\mathrm {fw} }}}+z}$$

dónde

• ${\displaystyle h_{\mathrm {fw} }}$es la carga de agua dulce (longitud, medida en m o ft), y
• ${\displaystyle \rho _{\mathrm {fw} }}$es la densidad del agua dulce (masa por unidad de volumen, normalmente en kg·m ⁻³ )

El gradiente hidráulico es un gradiente vectorial entre dos o más mediciones de carga hidráulica a lo largo de la longitud del recorrido del flujo. En el caso de las aguas subterráneas , también se denomina pendiente de Darcy , ya que determina la cantidad de un flujo o descarga de Darcy. También tiene aplicaciones en el flujo en canal abierto , donde también se lo conoce como gradiente de corriente , y se puede utilizar para determinar si un tramo está ganando o perdiendo energía. Se puede calcular un gradiente hidráulico adimensional entre dos puntos con valores de carga conocidos como: donde$${\displaystyle i={\frac {dh}{dl}}={\frac {h_{2}-h_{1}}{\mathrm {length} }}}$$

• ${\displaystyle i}$es el gradiente hidráulico (adimensional),
• ${\displaystyle dh}$es la diferencia entre dos cargas hidráulicas (longitud, generalmente en m o ft), y
• ${\displaystyle dl}$es la longitud del recorrido del flujo entre los dos piezómetros (longitud, generalmente en m o ft)

El gradiente hidráulico se puede expresar en notación vectorial, utilizando el operador del . Esto requiere un campo de carga hidráulica , que prácticamente solo se puede obtener a partir de modelos numéricos, como MODFLOW para aguas subterráneas o paso estándar o HEC-RAS para canales abiertos. En coordenadas cartesianas , esto se puede expresar como: Este vector describe la dirección del flujo de agua subterránea, donde los valores negativos indican flujo a lo largo de la dimensión y cero indica "sin flujo". Como con cualquier otro ejemplo en física, la energía debe fluir de alto a bajo, por lo que el flujo está en el gradiente negativo. Este vector se puede utilizar junto con la ley de Darcy y un tensor de conductividad hidráulica para determinar el flujo de agua en tres dimensiones.$${\displaystyle \nabla h=\left({\frac {\partial h}{\partial x}},{\frac {\partial h}{\partial y}},{\frac {\partial h}{\partial z}}\right)={\frac {\partial h}{\partial x}}\mathbf {i} +{\frac {\partial h}{\partial y}}\mathbf {j} +{\frac {\partial h}{\partial z}}\mathbf {k} }$$

Relación entre cargas para un caso hidrostático y un caso de flujo descendente .

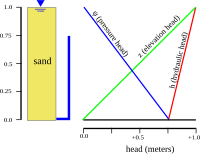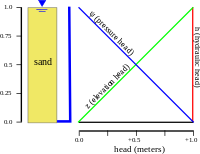
La distribución de la carga hidráulica a través de un acuífero determina hacia dónde fluirá el agua subterránea. En un ejemplo hidrostático (primera figura), donde la carga hidráulica es constante, no hay flujo. Sin embargo, si hay una diferencia en la carga hidráulica de arriba a abajo debido al drenaje desde abajo (segunda figura), el agua fluirá hacia abajo, debido a la diferencia de carga, también llamada gradiente hidráulico .

Aunque es una convención utilizar la presión manométrica en el cálculo de la carga hidráulica, es más correcto utilizar la presión absoluta (presión manométrica + presión atmosférica ), ya que es lo que realmente impulsa el flujo de agua subterránea. A menudo, no se dispone de observaciones detalladas de la presión barométrica en cada pozo a lo largo del tiempo, por lo que esto a menudo se ignora (lo que contribuye a grandes errores en lugares donde los gradientes hidráulicos son bajos o el ángulo entre pozos es agudo).

Los efectos de los cambios de presión atmosférica sobre los niveles de agua observados en los pozos se conocen desde hace muchos años. El efecto es directo: un aumento de la presión atmosférica supone un aumento de la carga sobre el agua del acuífero, lo que aumenta la profundidad del agua (reduce la elevación del nivel del agua). Pascal observó estos efectos de forma cualitativa por primera vez en el siglo XVII, y fueron descritos con más rigor por el físico de suelos Edgar Buckingham (que trabajaba para el Departamento de Agricultura de los Estados Unidos (USDA)) utilizando modelos de flujo de aire en 1907.

En cualquier fluido en movimiento real, la energía se disipa debido a la fricción ; la turbulencia disipa aún más energía para flujos con números de Reynolds altos. Esta disipación, llamada pérdida de carga , se divide en dos categorías principales, "pérdidas importantes" asociadas con la pérdida de energía por longitud de tubería y "pérdidas menores" asociadas con curvas, accesorios, válvulas, etc. La ecuación más común utilizada para calcular las pérdidas de carga importantes es la ecuación de Darcy-Weisbach . Los enfoques más antiguos y más empíricos son la ecuación de Hazen-Williams y la ecuación de Prony .

En sistemas de tuberías relativamente cortos, con una cantidad relativamente grande de curvas y accesorios, las pérdidas menores pueden superar fácilmente a las pérdidas mayores. En el diseño, las pérdidas menores se estiman generalmente a partir de tablas que utilizan coeficientes o una reducción más simple y menos precisa de las pérdidas menores a la longitud equivalente de la tubería, un método que se utiliza a menudo para realizar cálculos rápidos de la caída de presión en las líneas de transporte neumático. ^[4]

• Ecuación de Borda-Carnot
• Presión dinámica
• Pequeñas pérdidas en el flujo de las tuberías
• Cabeza dinámica total
• Etapa (hidrología)
• Cabeza (hidrología)
• Acumulador hidráulico

• Bear, J. 1972. Dinámica de fluidos en medios porosos , Dover. ISBN 0-486-65675-6 . 
• Para otras referencias que analizan la carga hidráulica en el contexto de la hidrogeología, consulte la sección de lectura adicional de esa página.