Alineación de secuencias múltiples

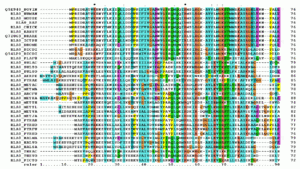
El alineamiento de secuencias múltiples ( MSA ) es el proceso o el resultado del alineamiento de secuencias de tres o más secuencias biológicas , generalmente proteínas , ADN o ARN . Estos alineamientos se utilizan para inferir relaciones evolutivas a través del análisis filogenético y pueden resaltar características homólogas entre secuencias. Los alineamientos resaltan eventos de mutación como mutaciones puntuales (cambios de un solo aminoácido o nucleótido ), mutaciones de inserción y mutaciones de deleción , y los alineamientos se utilizan para evaluar la conservación de secuencias e inferir la presencia y actividad de dominios de proteínas , estructuras terciarias , estructuras secundarias y aminoácidos o nucleótidos individuales.

Los alineamientos de secuencias múltiples requieren metodologías más sofisticadas que los alineamientos por pares , ya que son más complejos desde el punto de vista computacional . La mayoría de los programas de alineamiento de secuencias múltiples utilizan métodos heurísticos en lugar de optimización global porque identificar el alineamiento óptimo entre más de unas pocas secuencias de longitud moderada es prohibitivamente costoso desde el punto de vista computacional. Sin embargo, los métodos heurísticos generalmente no pueden garantizar soluciones de alta calidad y se ha demostrado que no logran generar soluciones casi óptimas en casos de prueba de referencia. ^{[1] [2] [3]}

Secuencias dadas , similares a la forma siguiente:${\estilo de visualización m}$$Estilo de visualización S_{i}}$${\displaystyle i=1,\cpuntos ,m}$

${\displaystyle S:={\begin{cases}S_{1}=(S_{11},S_{12},\ldots ,S_{1n_{1}})\\S_{2}=(S_{21},S_{22},\cdots ,S_{2n_{2}})\\\,\,\,\,\,\,\,\,\,\,\vdots \\S_{m}=(S_{m1},S_{m2},\ldots ,S_{mn_{m}})\end{cases}}}$

Se realiza una alineación de secuencias múltiples de este conjunto de secuencias insertando cualquier cantidad de espacios necesarios en cada una de las secuencias de hasta que las secuencias modificadas, , todas cumplan con la longitud y ningún valor en las secuencias de de la misma columna consista únicamente en espacios. La forma matemática de una alineación de secuencias múltiples del conjunto de secuencias anterior se muestra a continuación:${\estilo de visualización S}$$Estilo de visualización S_{i}}$${\estilo de visualización S}$$Estilo de visualización S'_{i}}$${\displaystyle L\geq \max\{n_{i}\mid i=1,\ldots ,m\}}$${\estilo de visualización S}$

${\displaystyle S':={\begin{cases}S'_{1}=(S'_{11},S'_{12},\ldots ,S'_{1L})\\S'_{2}=(S'_{21},S'_{22},\ldots ,S'_{2L})\\\,\,\,\,\,\,\,\,\,\,\,\vdots \\S'_{m}=(S'_{m1},S'_{m2},\ldots ,S'_{mL})\end{cases}}}$

Para regresar desde cada secuencia particular a , elimine todos los espacios.$Estilo de visualización S'_{i}}$$Estilo de visualización S_{i}}$

Un enfoque general al calcular alineaciones de secuencias múltiples es utilizar gráficos para identificar todas las alineaciones diferentes. Al buscar alineaciones mediante gráficos, se crea una alineación completa en un gráfico ponderado que contiene un conjunto de vértices y un conjunto de aristas. Cada una de las aristas del gráfico tiene un peso basado en una determinada heurística que ayuda a puntuar cada alineación o subconjunto del gráfico original.

Al determinar las alineaciones más adecuadas para cada MSA, generalmente se genera una traza . Una traza es un conjunto de vértices realizados , o correspondientes y alineados, que tiene un peso específico basado en los bordes que se seleccionan entre los vértices correspondientes. Al elegir trazas para un conjunto de secuencias, es necesario elegir una traza con un peso máximo para obtener la mejor alineación de las secuencias.

Existen varios métodos de alineación que se utilizan en múltiples secuencias para maximizar las puntuaciones y la exactitud de las alineaciones. Cada uno de ellos suele basarse en una determinada heurística con una perspectiva del proceso evolutivo. La mayoría intenta replicar la evolución para obtener la alineación más realista posible para predecir mejor las relaciones entre secuencias.

Un método directo para producir un MSA utiliza la técnica de programación dinámica para identificar la solución de alineación óptima a nivel global. Para las proteínas, este método generalmente implica dos conjuntos de parámetros: una penalización por espacio y una matriz de sustitución que asigna puntajes o probabilidades a la alineación de cada par posible de aminoácidos en función de la similitud de las propiedades químicas de los aminoácidos y la probabilidad evolutiva de la mutación. Para las secuencias de nucleótidos, se utiliza una penalización por espacio similar, pero es típica una matriz de sustitución mucho más simple, en la que solo se consideran las coincidencias y los desajustes idénticos. Los puntajes en la matriz de sustitución pueden ser todos positivos o una mezcla de positivos y negativos en el caso de una alineación global, pero deben ser tanto positivos como negativos, en el caso de una alineación local. ^[4]

Para n secuencias individuales, el método ingenuo requiere construir el equivalente n -dimensional de la matriz formada en el alineamiento de secuencia por pares estándar . El espacio de búsqueda aumenta exponencialmente con el aumento de n y también depende en gran medida de la longitud de la secuencia. Expresado con la notación O grande comúnmente utilizada para medir la complejidad computacional , un MSA ingenuo toma O(Longitud ^Nseqs ) tiempo para producirse. Se ha demostrado que encontrar el óptimo global para n secuencias de esta manera es un problema NP-completo . ^{[5] [6] [7]} En 1989, basado en el algoritmo de Carrillo-Lipman, ^[8] Altschul introdujo un método práctico que utiliza alineaciones por pares para restringir el espacio de búsqueda n-dimensional. ^[9] En este enfoque, se realizan alineaciones de programación dinámica por pares en cada par de secuencias en el conjunto de consulta, y solo se busca el espacio cerca de la intersección n-dimensional de estas alineaciones para la alineación n-direccional. El programa MSA optimiza la suma de todos los pares de caracteres en cada posición de la alineación (la llamada suma de la puntuación de pares) y se ha implementado en un programa de software para construir alineaciones de secuencias múltiples. ^[10] En 2019, Hosseininasab y van Hoeve demostraron que mediante el uso de diagramas de decisión, MSA puede modelarse en complejidad de espacio polinomial. ^[3]

El método más utilizado para alineaciones de secuencias múltiples utiliza una búsqueda heurística conocida como técnica progresiva (también conocida como método jerárquico o de árbol) desarrollada por Da-Fei Feng y Doolittle en 1987. ^[11] La alineación progresiva construye un MSA final combinando alineaciones por pares comenzando con el par más similar y progresando hasta el más distantemente relacionado. Todos los métodos de alineación progresiva requieren dos etapas: una primera etapa en la que las relaciones entre las secuencias se representan como un árbol filogenético , llamado árbol guía , y un segundo paso en el que se construye el MSA agregando las secuencias secuencialmente al MSA creciente de acuerdo con el árbol guía. El árbol guía inicial se determina mediante un método de agrupamiento eficiente como la unión de vecinos o el método de grupo de pares no ponderados con media aritmética ( UPGMA ), y puede usar distancias basadas en el número de subsecuencias idénticas de dos letras (como en FASTA en lugar de una alineación de programación dinámica). ^[12]

No se garantiza que los alineamientos progresivos sean globalmente óptimos. El problema principal es que cuando se cometen errores en cualquier etapa del crecimiento del MSA, estos errores se propagan hasta el resultado final. El rendimiento también es particularmente malo cuando todas las secuencias del conjunto están relacionadas de manera bastante distante. La mayoría de los métodos progresivos modernos modifican su función de puntuación con una función de ponderación secundaria que asigna factores de escala a los miembros individuales del conjunto de consulta de manera no lineal en función de su distancia filogenética con respecto a sus vecinos más cercanos. Esto corrige la selección no aleatoria de las secuencias entregadas al programa de alineamiento. ^[12]

Los métodos de alineamiento progresivo son lo suficientemente eficientes para implementarse a gran escala para muchas secuencias (de cientos a miles). Un método de alineamiento progresivo popular ha sido la familia Clustal . ^{[13] [14]} Clustal W se usa ampliamente para la construcción de árboles filogenéticos, a pesar de las advertencias explícitas del autor de que no se deben usar alineaciones sin editar en dichos estudios y como entrada para la predicción de la estructura de proteínas mediante modelado de homología. El Instituto Europeo de Bioinformática (EMBL-EBI) anunció que CLustalW2 expirará en agosto de 2015. Recomiendan Clustal Omega, que funciona en base a árboles guía sembrados y técnicas de perfil-perfil HMM para alineamientos de proteínas. Una herramienta alternativa para alineamientos progresivos de ADN es el alineamiento múltiple utilizando la transformada rápida de Fourier ( MAFFT ). ^[15]

Otro método común de alineamiento progresivo llamado T-Coffee ^[16] es más lento que Clustal y sus derivados, pero generalmente produce alineamientos más precisos para conjuntos de secuencias distantes. T-Coffee calcula alineamientos por pares combinando el alineamiento directo del par con alineamientos indirectos que alinean cada secuencia del par con una tercera secuencia. Utiliza el resultado de Clustal, así como otro programa de alineamiento local LALIGN, que encuentra múltiples regiones de alineamiento local entre dos secuencias. El alineamiento resultante y el árbol filogenético se utilizan como guía para producir factores de ponderación nuevos y más precisos.

Debido a que los métodos progresivos son heurísticas que no tienen garantía de convergencia hacia un óptimo global, la calidad de la alineación puede ser difícil de evaluar y su verdadero significado biológico puede ser obscuro. En el programa PSAlign se ha implementado un método semi-progresivo que mejora la calidad de la alineación y no utiliza una heurística con pérdida mientras se ejecuta en tiempo polinomial . ^[17]

Un conjunto de métodos para producir MSAs mientras se reducen los errores inherentes a los métodos progresivos se clasifican como "iterativos" porque funcionan de manera similar a los métodos progresivos pero realinean repetidamente las secuencias iniciales y agregan nuevas secuencias al MSA creciente. Una razón por la que los métodos progresivos dependen tanto de una alineación inicial de alta calidad es el hecho de que estas alineaciones siempre se incorporan al resultado final, es decir, una vez que una secuencia se ha alineado en el MSA, su alineación no se considera más. Esta aproximación mejora la eficiencia a costa de la precisión. Por el contrario, los métodos iterativos pueden volver a alineaciones por pares calculadas previamente o sub-MSAs que incorporan subconjuntos de la secuencia de consulta como un medio para optimizar una función objetivo general , como encontrar una puntuación de alineación de alta calidad. ^[12]

Se han implementado y puesto a disposición en paquetes de software una variedad de métodos de iteración sutilmente diferentes; las revisiones y comparaciones han sido útiles pero generalmente se abstienen de elegir una técnica "mejor". ^[18] El paquete de software PRRN/PRRP utiliza un algoritmo de escalada de colinas para optimizar su puntaje de alineación de MSA ^[19] y corrige iterativamente tanto los pesos de alineación como las regiones localmente divergentes o "con brechas" del MSA en crecimiento. ^[12] PRRP funciona mejor cuando refina una alineación construida previamente con un método más rápido. ^[12]

Otro programa iterativo, DIALIGN, adopta un enfoque inusual al centrarse estrictamente en las alineaciones locales entre subsegmentos o motivos de secuencia sin introducir una penalización por espacio. ^[20] La alineación de motivos individuales se logra entonces con una representación matricial similar a un gráfico de matriz de puntos en una alineación por pares. Un método alternativo que utiliza alineaciones locales rápidas como puntos de anclaje o semillas para un procedimiento de alineación global más lento se implementa en la suite CHAOS/DIALIGN. ^[20]

Un tercer método popular basado en iteraciones llamado MUSCLE (alineación de secuencias múltiples por expectativa logarítmica) mejora los métodos progresivos con una medida de distancia más precisa para evaluar la relación de dos secuencias. ^[21] La medida de distancia se actualiza entre las etapas de iteración (aunque, en su forma original, MUSCLE contenía solo 2-3 iteraciones dependiendo de si el refinamiento estaba habilitado).

Los métodos de consenso intentan encontrar la alineación óptima de múltiples secuencias dadas múltiples alineaciones diferentes del mismo conjunto de secuencias. Hay dos métodos de consenso comúnmente utilizados, M-COFFEE y MergeAlign. ^[22] M-COFFEE utiliza alineaciones de secuencias múltiples generadas por siete métodos diferentes para generar alineaciones de consenso. MergeAlign es capaz de generar alineaciones de consenso a partir de cualquier número de alineaciones de entrada generadas utilizando diferentes modelos de evolución de secuencias o diferentes métodos de alineación de secuencias múltiples. La opción predeterminada para MergeAlign es inferir una alineación de consenso utilizando alineaciones generadas utilizando 91 modelos diferentes de evolución de secuencias de proteínas.

Un modelo oculto de Markov (HMM) es un modelo probabilístico que puede asignar probabilidades a todas las combinaciones posibles de brechas, coincidencias y desajustes, para determinar el MSA más probable o el conjunto de MSA posibles. Los HMM pueden producir un único resultado con la puntuación más alta, pero también pueden generar una familia de posibles alineaciones que luego se pueden evaluar para determinar su importancia biológica. Los HMM pueden producir alineaciones tanto globales como locales. Aunque los métodos basados ​​en HMM se han desarrollado hace relativamente poco tiempo, ofrecen mejoras significativas en la velocidad computacional, especialmente para secuencias que contienen regiones superpuestas. ^[12]

Los métodos típicos basados ​​en HMM funcionan representando un MSA como una forma de gráfico acíclico dirigido conocido como gráfico de orden parcial, que consiste en una serie de nodos que representan posibles entradas en las columnas de un MSA. En esta representación, una columna que se conserva absolutamente (es decir, que todas las secuencias en el MSA comparten un carácter particular en una posición particular) se codifica como un solo nodo con tantas conexiones salientes como caracteres posibles haya en la siguiente columna de la alineación. En términos de un modelo Markov oculto típico, los estados observados son las columnas de alineación individuales y los estados "ocultos" representan la supuesta secuencia ancestral de la que se supone que descienden las secuencias en el conjunto de consulta. Una variante de búsqueda eficiente del método de programación dinámica, denominada algoritmo de Viterbi , se utiliza generalmente para alinear sucesivamente el MSA creciente con la siguiente secuencia en el conjunto de consulta para producir un nuevo MSA. ^[23] Esto es distinto de los métodos de alineación progresiva porque la alineación de secuencias anteriores se actualiza en cada nueva adición de secuencia. Sin embargo, al igual que los métodos progresivos, esta técnica puede verse influenciada por el orden en el que las secuencias del conjunto de consulta se integran en la alineación, especialmente cuando las secuencias están distantemente relacionadas. ^[12]

Existen varios programas de software disponibles en los que se han implementado variantes de métodos basados ​​en HMM y que se destacan por su escalabilidad y eficiencia, aunque usar correctamente un método HMM es más complejo que usar métodos progresivos más comunes. El más simple es Partial-Order Alignment (POA), ^[24] y un método similar más general se implementa en el paquete de software Sequence Alignment and Modeling System (SAM). ^[25] y HMMER . ^[26] SAM se ha utilizado como una fuente de alineaciones para la predicción de la estructura de proteínas para participar en el experimento de predicción de estructura Critical Assessment of Structure Prediction ( CASP ) y para desarrollar una base de datos de proteínas predichas en la especie de levadura S. cerevisiae . HHsearch ^[27] es un paquete de software para la detección de secuencias de proteínas relacionadas de forma remota basado en la comparación por pares de HMM. Un servidor que ejecuta HHsearch ( HHpred ) fue el más rápido de los 10 servidores de predicción de estructura automática en las competiciones de predicción de estructura CASP7 y CASP8. ^[28]

La mayoría de los métodos de alineamiento de secuencias múltiples intentan minimizar el número de inserciones/deleciones (huecos) y, como consecuencia, producen alineamientos compactos. Esto causa varios problemas si las secuencias a alinear contienen regiones no homólogas , si los huecos son informativos en un análisis de filogenia . Estos problemas son comunes en secuencias recién producidas que están mal anotadas y pueden contener cambios de marco , dominios erróneos o exones empalmados no homólogos . El primer método de este tipo fue desarrollado en 2005 por Löytynoja y Goldman. ^[29] Los mismos autores lanzaron un paquete de software llamado PRANK en 2008. ^[30] PRANK mejora los alineamientos cuando hay inserciones. Sin embargo, se ejecuta lentamente en comparación con los métodos progresivos y/o iterativos que se han desarrollado durante varios años.

En 2012, aparecieron dos nuevas herramientas que tienen en cuenta la filogenia. Una se llama PAGAN y fue desarrollada por el mismo equipo que PRANK. ^[31] La otra es ProGraphMSA, desarrollada por Szalkowski. ^[32] Ambos paquetes de software se desarrollaron de forma independiente, pero comparten características comunes, en particular el uso de algoritmos de gráficos para mejorar el reconocimiento de regiones no homólogas y una mejora en el código que hace que estos programas sean más rápidos que PRANK.

La búsqueda de motivos, también conocida como análisis de perfiles, es un método para localizar motivos de secuencias en MSA globales que es a la vez un medio para producir un mejor MSA y un medio para producir una matriz de puntuación para su uso en la búsqueda de otras secuencias de motivos similares. Se han desarrollado diversos métodos para aislar los motivos, pero todos se basan en la identificación de patrones cortos altamente conservados dentro de la alineación más grande y la construcción de una matriz similar a una matriz de sustitución que refleje la composición de aminoácidos o nucleótidos de cada posición en el motivo putativo. La alineación se puede refinar luego utilizando estas matrices. En el análisis de perfiles estándar, la matriz incluye entradas para cada carácter posible, así como entradas para espacios vacíos. ^[12] Alternativamente, los algoritmos estadísticos de búsqueda de patrones pueden identificar motivos como precursores de un MSA en lugar de como una derivación. En muchos casos, cuando el conjunto de consulta contiene solo una pequeña cantidad de secuencias o contiene solo secuencias altamente relacionadas, se agregan pseudoconteos para normalizar la distribución reflejada en la matriz de puntuación. En particular, esto corrige las entradas de probabilidad cero en la matriz a valores que son pequeños pero distintos de cero.

El análisis de bloques es un método de búsqueda de motivos que restringe los motivos a regiones sin espacios en la alineación. Los bloques se pueden generar a partir de un MSA o se pueden extraer de secuencias no alineadas utilizando un conjunto precalculado de motivos comunes generados previamente a partir de familias de genes conocidas. ^[33] La puntuación de bloques generalmente se basa en el espaciado de caracteres de alta frecuencia en lugar del cálculo de una matriz de sustitución explícita.

La comparación de patrones estadísticos se ha implementado utilizando tanto el algoritmo de maximización de expectativas como el muestreador de Gibbs . Una de las herramientas de búsqueda de motivos más comunes, llamada Multiple EM for Motif Elicitation (MEME), utiliza la maximización de expectativas y los métodos ocultos de Markov para generar motivos que luego se utilizan como herramientas de búsqueda por su complemento MAST en el conjunto combinado MEME/MAST. ^{[34] [35]}

Las regiones de ADN no codificantes, especialmente los sitios de unión de factores de transcripción (TFBS), se conservan, pero no necesariamente están relacionadas evolutivamente, y pueden haber convergido a partir de ancestros no comunes. Por lo tanto, las suposiciones utilizadas para alinear secuencias de proteínas y regiones codificantes de ADN son inherentemente diferentes de las que se aplican a las secuencias TFBS. Aunque es significativo alinear regiones codificantes de ADN para secuencias homólogas utilizando operadores de mutación, la alineación de secuencias de sitios de unión para el mismo factor de transcripción no puede depender de operaciones de mutación relacionadas con la evolución. De manera similar, el operador evolutivo de mutaciones puntuales se puede utilizar para definir una distancia de edición para secuencias codificantes, pero esto tiene poco significado para las secuencias TFBS porque cualquier variación de secuencia tiene que mantener un cierto nivel de especificidad para que el sitio de unión funcione. Esto se vuelve especialmente importante cuando se intenta alinear secuencias TFBS conocidas para construir modelos supervisados ​​para predecir ubicaciones desconocidas del mismo TFBS. Por lo tanto, los métodos de alineamiento de secuencias múltiples deben ajustar la hipótesis evolutiva subyacente y los operadores utilizados como en el trabajo publicado que incorpora información termodinámica de base vecina ^[36] para alinear los sitios de unión buscando el alineamiento termodinámico más bajo que conserve la especificidad del sitio de unión.

Las técnicas de optimización estándar en informática (ambas inspiradas en procesos físicos, pero que no los reproducen directamente) también se han utilizado en un intento de producir de manera más eficiente MSA de calidad. Una de esas técnicas, los algoritmos genéticos , se ha utilizado para la producción de MSA en un intento de simular ampliamente el proceso evolutivo hipotético que dio lugar a la divergencia en el conjunto de consulta. El método funciona dividiendo una serie de posibles MSA en fragmentos y reorganizando repetidamente esos fragmentos con la introducción de espacios en distintas posiciones. Durante la simulación se optimiza una función objetivo general , más generalmente la función de maximización de "suma de pares" introducida en los métodos MSA basados ​​en programación dinámica. Se ha implementado una técnica para secuencias de proteínas en el programa de software SAGA (Sequence Alignment by Genetic Algorithm) ^[37] y su equivalente en ARN se llama RAGA. ^[38]

La técnica de recocido simulado , mediante la cual un MSA existente producido por otro método se refina mediante una serie de reordenamientos diseñados para encontrar mejores regiones del espacio de alineación que la que ya ocupa la alineación de entrada. Al igual que el método del algoritmo genético, el recocido simulado maximiza una función objetivo como la función de suma de pares. El recocido simulado utiliza un "factor de temperatura" metafórico que determina la velocidad a la que se producen los reordenamientos y la probabilidad de cada reordenamiento; el uso típico alterna períodos de altas tasas de reordenamiento con probabilidad relativamente baja (para explorar regiones más distantes del espacio de alineación) con períodos de tasas más bajas y mayores probabilidades para explorar más a fondo los mínimos locales cerca de las regiones recientemente "colonizadas". Este enfoque se ha implementado en el programa MSASA (Multiple Sequence Alignment by Simulated Annealing). ^[39]

La programación matemática y, en particular, los modelos de programación entera mixta son otro enfoque para resolver problemas MSA. La ventaja de dichos modelos de optimización es que se pueden utilizar para encontrar la solución MSA óptima de manera más eficiente en comparación con el enfoque DP tradicional. Esto se debe, en parte, a la aplicabilidad de las técnicas de descomposición para programas matemáticos, donde el modelo MSA se descompone en partes más pequeñas y se resuelve iterativamente hasta que se encuentra la solución óptima. Los algoritmos de ejemplo utilizados para resolver modelos de programación entera mixta de MSA incluyen la rama y el precio ^[40] y la descomposición de Benders ^[3] . Aunque los enfoques exactos son computacionalmente lentos en comparación con los algoritmos heurísticos para MSA, se garantiza que alcanzarán la solución óptima eventualmente, incluso para problemas de gran tamaño.

En enero de 2017, D-Wave Systems anunció que su software de computación cuántica de código abierto qbsolv se había utilizado con éxito para encontrar una solución más rápida al problema MSA. ^[41]

El uso necesario de heurísticas para el alineamiento múltiple significa que para un conjunto arbitrario de proteínas, siempre hay una buena probabilidad de que un alineamiento contenga errores. Por ejemplo, una evaluación de varios programas de alineamiento líderes utilizando el punto de referencia BAliBase encontró que al menos el 24% de todos los pares de aminoácidos alineados estaban alineados incorrectamente. ^[2] Estos errores pueden surgir debido a inserciones únicas en una o más regiones de secuencias, o a través de algún proceso evolutivo más complejo que conduce a proteínas que no se alinean fácilmente por secuencia solamente. A medida que aumenta el número de secuencias y su divergencia, se cometerán muchos más errores simplemente debido a la naturaleza heurística de los algoritmos MSA. Los visores de alineamiento de secuencias múltiples permiten revisar visualmente los alineamientos, a menudo inspeccionando la calidad del alineamiento para sitios funcionales anotados en dos o más secuencias. Muchos también permiten editar el alineamiento para corregir estos errores (generalmente menores), con el fin de obtener un alineamiento "curado" óptimo adecuado para su uso en análisis filogenético o modelado comparativo. ^[42]

Sin embargo, a medida que aumenta el número de secuencias y especialmente en estudios de todo el genoma que involucran muchos MSA, es imposible curar manualmente todas las alineaciones. Además, la curación manual es subjetiva. Y finalmente, incluso el mejor experto no puede alinear con confianza los casos más ambiguos de secuencias altamente divergentes. En tales casos, es una práctica común utilizar procedimientos automáticos para excluir regiones alineadas de manera poco confiable del MSA. Para el propósito de la reconstrucción de la filogenia (ver más abajo) el programa Gblocks se utiliza ampliamente para eliminar bloques de alineación sospechosos de baja calidad, de acuerdo con varios puntos de corte en el número de secuencias con huecos en las columnas de alineación. ^[43] Sin embargo, estos criterios pueden filtrar excesivamente las regiones con eventos de inserción/eliminación que aún pueden estar alineadas de manera confiable, y estas regiones podrían ser deseables para otros fines, como la detección de selección positiva. Algunos algoritmos de alineación generan puntajes específicos del sitio que permiten la selección de regiones de alta confianza. Un servicio de este tipo fue ofrecido por primera vez por el programa SOAP ^[44], que prueba la robustez de cada columna a la perturbación en los parámetros del popular programa de alineación CLUSTALW. El programa T-Coffee ^[45] utiliza una biblioteca de alineaciones en la construcción del MSA final, y su MSA de salida está coloreado de acuerdo con las puntuaciones de confianza que reflejan el acuerdo entre diferentes alineaciones en la biblioteca con respecto a cada residuo alineado. Su extensión, Transitive Consistency Score (TCS), utiliza bibliotecas T-Coffee de alineaciones por pares para evaluar cualquier MSA de terceros. Las proyecciones por pares se pueden producir utilizando métodos rápidos o lentos, lo que permite un equilibrio entre velocidad y precisión. ^{[46] [47]} Otro programa de alineación que puede generar un MSA con puntuaciones de confianza es FSA ^[48] , que utiliza un modelo estadístico que permite el cálculo de la incertidumbre en la alineación. La puntuación HoT (Heads-Or-Tails) se puede utilizar como una medida de la incertidumbre de alineación específica del sitio debido a la existencia de múltiples soluciones coóptimas. ^[49] El programa GUIDANCE ^[50] calcula una medida de confianza específica del sitio similar basada en la robustez de la alineación a la incertidumbre en el árbol guía que se utiliza en los programas de alineación progresiva. Un enfoque alternativo, más justificado estadísticamente para evaluar la incertidumbre de la alineación es el uso de modelos evolutivos probabilísticos para la estimación conjunta de la filogenia y la alineación. Un enfoque bayesiano permite el cálculo de probabilidades posteriores de la filogenia y la alineación estimadas, que es una medida de la confianza en estas estimaciones. En este caso, se puede calcular una probabilidad posterior para cada sitio en la alineación. Este enfoque se implementó en el programa BAli-Phy. ^[51]

Hay programas gratuitos disponibles para la visualización de alineaciones de secuencias múltiples, por ejemplo, Jalview y UGENE .

Se pueden utilizar alineaciones de secuencias múltiples para crear un árbol filogenético . ^[52] Esto es posible por dos razones. La primera es porque los dominios funcionales que se conocen en secuencias anotadas se pueden utilizar para la alineación en secuencias no anotadas. La otra es que se pueden encontrar regiones conservadas que se sabe que son funcionalmente importantes. Esto hace posible que se utilicen alineaciones de secuencias múltiples para analizar y encontrar relaciones evolutivas a través de la homología entre secuencias. Se pueden detectar mutaciones puntuales y eventos de inserción o eliminación (llamados indels).

Los alineamientos de secuencias múltiples también se pueden utilizar para identificar sitios funcionalmente importantes, como sitios de unión, sitios activos o sitios correspondientes a otras funciones clave, mediante la localización de dominios conservados. Al observar alineamientos de secuencias múltiples, es útil considerar diferentes aspectos de las secuencias al comparar secuencias. Estos aspectos incluyen identidad, similitud y homología. Identidad significa que las secuencias tienen residuos idénticos en sus respectivas posiciones. Por otro lado, la similitud tiene que ver con que las secuencias que se comparan tengan residuos similares cuantitativamente. Por ejemplo, en términos de secuencias de nucleótidos, las pirimidinas se consideran similares entre sí, al igual que las purinas. La similitud en última instancia conduce a la homología, en el sentido de que cuanto más similares son las secuencias, más cerca están de ser homólogas. Esta similitud en las secuencias puede luego ayudar a encontrar un ancestro común. ^[52]

• Análisis de secuencia sin alineamiento
• Cladística
• Alineación generalizada de árboles
• Visualizadores de alineamiento de secuencias múltiples
• PANDIT , una base de datos biológica que cubre dominios proteicos
• Filogenética
• Software de alineación de secuencias
• Alineación estructural

• Duret, L.; S. Abdeddaim (2000). "Alineamiento múltiple para análisis filogenéticos o funcionales estructurales de secuencias homólogas". En D. Higgins y W. Taylor (ed.). Estructura de secuencias bioinformáticas y bancos de datos . Oxford: Oxford University Press.
• Notredame, C. (2002). "Progresos recientes en el alineamiento de secuencias múltiples: un estudio". Farmacogenómica . 3 (1): 131–144. doi :10.1517/14622416.3.1.131. PMID  11966409.
• Thompson, JD; Plewniak, F.; Poch, O. (1999). "Una comparación exhaustiva de programas de alineamiento de secuencias múltiples". Nucleic Acids Research . 27 (13): 12682–2690. doi :10.1093/nar/27.13.2682. PMC  148477 . PMID  10373585.
• Wallace, IM; Blackshields, G.; Higgins, DG (2005). "Alineamientos de secuencias múltiples". Curr Opin Struct Biol . 15 (3): 261–266. doi :10.1016/j.sbi.2005.04.002. PMID  15963889.
• Notredame, C (2007). "Evoluciones recientes de algoritmos de alineamiento de secuencias múltiples". PLOS Computational Biology . 3 (8): e123. Bibcode :2007PLSCB...3..123N. doi : 10.1371/journal.pcbi.0030123 . PMC  1963500 . PMID  17784778.

• Herramientas de alineación de secuencias ExPASy
• Página de recursos archivada sobre alineamiento múltiple: de la Escuela Virtual de Ciencias Naturales
• Herramientas para múltiples alineamientos: de Pôle Bioinformatique Lyonnais
• Un punto de entrada a servidores y a información agrupados
• Un punto de entrada a los principales servidores de T-Coffee
• Un punto de entrada al servidor principal de MergeAlign y a la información
• Servidores del Instituto Europeo de Bioinformática:
  • ClustalW2 – programa de alineación de secuencias múltiples de propósito general para ADN o proteínas.
  • Músculo: comparación de múltiples secuencias por expectativa logarítmica
  • T-coffee – alineamiento de secuencias múltiples.
  • MAFFT – Alineación múltiple mediante la transformada rápida de Fourier
  • KALIGN: un algoritmo de alineación de secuencias múltiples rápido y preciso.

• Conferencias sobre alineamiento de secuencias múltiples – del Instituto Max Planck de Genética Molecular
• Apuntes y ejercicios prácticos sobre alineamientos de secuencias múltiples en el Laboratorio Europeo de Biología Molecular (EMBL)
• Apuntes de la clase de bioinformática molecular
• Apuntes de la clase sobre evolución molecular y bioinformática