Teoría de la complejidad computacional
En la informática teórica y las matemáticas, la teoría de la complejidad computacional se centra en la clasificación de los problemas computacionales según el uso de recursos y explora las relaciones entre estas clasificaciones. Un problema computacional es una tarea resuelta por una computadora. Un problema computacional se puede resolver mediante la aplicación mecánica de pasos matemáticos, como un algoritmo .
Un problema se considera inherentemente difícil si su solución requiere recursos significativos, sea cual sea el algoritmo utilizado. La teoría formaliza esta intuición, introduciendo modelos matemáticos de computación para estudiar estos problemas y cuantificando su complejidad computacional , es decir, la cantidad de recursos necesarios para resolverlos, como tiempo y almacenamiento. También se utilizan otras medidas de complejidad, como la cantidad de comunicación (utilizada en complejidad de comunicación ), el número de puertas en un circuito (utilizado en complejidad de circuito ) y el número de procesadores (utilizado en computación paralela ). Una de las funciones de la teoría de la complejidad computacional es determinar los límites prácticos de lo que las computadoras pueden y no pueden hacer. El problema P versus NP , uno de los siete Problemas del Premio del Milenio , [1] es parte del campo de la complejidad computacional.
Campos estrechamente relacionados en la informática teórica son el análisis de algoritmos y la teoría de la computabilidad . Una distinción clave entre el análisis de algoritmos y la teoría de la complejidad computacional es que el primero se dedica a analizar la cantidad de recursos que necesita un algoritmo particular para resolver un problema, mientras que la segunda plantea una pregunta más general sobre todos los algoritmos posibles que podrían usarse para resolver el mismo problema. Más precisamente, la teoría de la complejidad computacional intenta clasificar los problemas que pueden o no resolverse con recursos restringidos adecuadamente. A su vez, imponer restricciones a los recursos disponibles es lo que distingue la complejidad computacional de la teoría de la computabilidad: esta última teoría pregunta qué tipos de problemas pueden, en principio, resolverse algorítmicamente.
Problemas computacionales
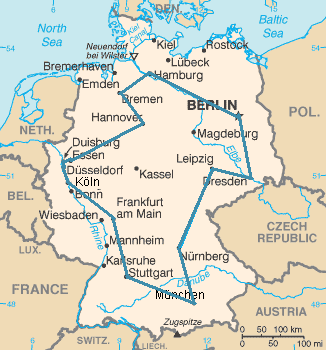
Instancias problemáticas
Un problema computacional puede verse como una colección infinita de instancias junto con un conjunto (posiblemente vacío) de soluciones para cada instancia. La cadena de entrada para un problema computacional se conoce como una instancia de problema y no debe confundirse con el problema en sí. En la teoría de la complejidad computacional, un problema se refiere a la pregunta abstracta que se debe resolver. En contraste, una instancia de este problema es un enunciado más bien concreto, que puede servir como entrada para un problema de decisión. Por ejemplo, considere el problema de la prueba de primalidad . La instancia es un número (por ejemplo, 15) y la solución es "sí" si el número es primo y "no" en caso contrario (en este caso, 15 no es primo y la respuesta es "no"). Dicho de otra manera, la instancia es una entrada particular al problema y la solución es la salida correspondiente a la entrada dada.
Para resaltar aún más la diferencia entre un problema y una instancia, considere la siguiente instancia de la versión de decisión del problema del viajante : ¿Existe una ruta de 2000 kilómetros como máximo que pase por las 15 ciudades más grandes de Alemania? La respuesta cuantitativa a esta instancia de problema en particular es de poca utilidad para resolver otras instancias del problema, como pedir un viaje de ida y vuelta a través de todos los sitios en Milán cuya longitud total sea de 10 km como máximo. Por esta razón, la teoría de la complejidad aborda problemas computacionales y no instancias de problemas particulares.
Representación de instancias de problemas
Al considerar problemas computacionales, una instancia de problema es una cadena sobre un alfabeto . Por lo general, se considera que el alfabeto es el alfabeto binario (es decir, el conjunto {0,1}) y, por lo tanto, las cadenas son cadenas de bits . Al igual que en una computadora del mundo real , los objetos matemáticos que no sean cadenas de bits deben codificarse adecuadamente. Por ejemplo, los números enteros se pueden representar en notación binaria y los gráficos se pueden codificar directamente a través de sus matrices de adyacencia o codificando sus listas de adyacencia en binario.
Aunque algunas demostraciones de teoremas de teoría de la complejidad suponen regularmente una elección concreta de codificación de entrada, se intenta mantener la discusión lo suficientemente abstracta como para que sea independiente de la elección de codificación. Esto se puede lograr asegurando que diferentes representaciones puedan transformarse entre sí de manera eficiente.
Problemas de decisión como lenguajes formales

Los problemas de decisión son uno de los objetos centrales de estudio en la teoría de la complejidad computacional. Un problema de decisión es un tipo de problema computacional donde la respuesta es sí o no (alternativamente, 1 o 0). Un problema de decisión puede verse como un lenguaje formal , donde los miembros del lenguaje son instancias cuya salida es sí, y los no miembros son aquellas instancias cuya salida es no. El objetivo es decidir, con la ayuda de un algoritmo , si una cadena de entrada dada es un miembro del lenguaje formal en consideración. Si el algoritmo que decide este problema devuelve la respuesta sí , se dice que el algoritmo acepta la cadena de entrada, de lo contrario se dice que rechaza la entrada.
Un ejemplo de un problema de decisión es el siguiente. La entrada es un grafo arbitrario . El problema consiste en decidir si el grafo dado es conexo o no. El lenguaje formal asociado con este problema de decisión es entonces el conjunto de todos los grafos conexos; para obtener una definición precisa de este lenguaje, uno tiene que decidir cómo se codifican los grafos como cadenas binarias.
Problemas de función
Un problema de función es un problema computacional en el que se espera una única salida (de una función total ) para cada entrada, pero la salida es más compleja que la de un problema de decisión , es decir, la salida no es simplemente sí o no. Algunos ejemplos notables incluyen el problema del viajante y el problema de factorización de números enteros .
Es tentador pensar que la noción de problemas de función es mucho más rica que la de problemas de decisión. Sin embargo, en realidad no es así, ya que los problemas de función pueden reformularse como problemas de decisión. Por ejemplo, la multiplicación de dos números enteros puede expresarse como el conjunto de ternas en las que se cumple la relación. Decidir si una terna dada es miembro de este conjunto corresponde a resolver el problema de multiplicar dos números.
Medición del tamaño de una instancia
Para medir la dificultad de resolver un problema computacional, se puede querer ver cuánto tiempo requiere el mejor algoritmo para resolver el problema. Sin embargo, el tiempo de ejecución puede, en general, depender de la instancia. En particular, las instancias más grandes requerirán más tiempo para resolverse. Por lo tanto, el tiempo requerido para resolver un problema (o el espacio requerido, o cualquier medida de complejidad) se calcula como una función del tamaño de la instancia. El tamaño de entrada se mide típicamente en bits. La teoría de la complejidad estudia cómo los algoritmos escalan a medida que aumenta el tamaño de entrada. Por ejemplo, en el problema de encontrar si un grafo está conectado, ¿cuánto tiempo más lleva resolver un problema para un grafo con vértices en comparación con el tiempo que lleva para un grafo con vértices?
Si el tamaño de entrada es , el tiempo empleado puede expresarse como una función de . Dado que el tiempo empleado en diferentes entradas del mismo tamaño puede ser diferente, la complejidad temporal del peor caso se define como el tiempo máximo empleado en todas las entradas de tamaño . Si es un polinomio en , entonces se dice que el algoritmo es un algoritmo de tiempo polinomial . La tesis de Cobham sostiene que un problema puede resolverse con una cantidad factible de recursos si admite un algoritmo de tiempo polinomial.
Modelos de máquinas y medidas de complejidad
Máquina de Turing

Una máquina de Turing es un modelo matemático de una máquina de computación general. Es un dispositivo teórico que manipula símbolos contenidos en una tira de cinta. Las máquinas de Turing no están pensadas como una tecnología informática práctica, sino como un modelo general de una máquina de computación: cualquier cosa, desde una supercomputadora avanzada hasta un matemático con un lápiz y un papel. Se cree que si un problema puede resolverse mediante un algoritmo, existe una máquina de Turing que resuelve el problema. De hecho, esta es la afirmación de la tesis de Church-Turing . Además, se sabe que todo lo que se puede calcular en otros modelos de computación conocidos por nosotros hoy, como una máquina RAM , el Juego de la vida de Conway , los autómatas celulares , el cálculo lambda o cualquier lenguaje de programación, se puede calcular en una máquina de Turing. Dado que las máquinas de Turing son fáciles de analizar matemáticamente y se cree que son tan poderosas como cualquier otro modelo de computación, la máquina de Turing es el modelo más utilizado en la teoría de la complejidad.
Se utilizan muchos tipos de máquinas de Turing para definir clases de complejidad, como máquinas de Turing deterministas , máquinas de Turing probabilísticas , máquinas de Turing no deterministas , máquinas de Turing cuánticas , máquinas de Turing simétricas y máquinas de Turing alternas . En principio, todas son igualmente poderosas, pero cuando los recursos (como el tiempo o el espacio) están limitados, algunas de ellas pueden ser más poderosas que otras.
Una máquina de Turing determinista es la máquina de Turing más básica, que utiliza un conjunto fijo de reglas para determinar sus acciones futuras. Una máquina de Turing probabilística es una máquina de Turing determinista con un suministro adicional de bits aleatorios. La capacidad de tomar decisiones probabilísticas a menudo ayuda a los algoritmos a resolver problemas de manera más eficiente. Los algoritmos que utilizan bits aleatorios se denominan algoritmos aleatorios . Una máquina de Turing no determinista es una máquina de Turing determinista con una característica adicional de no determinismo, que permite que una máquina de Turing tenga múltiples acciones futuras posibles a partir de un estado dado. Una forma de ver el no determinismo es que la máquina de Turing se ramifica en muchos caminos computacionales posibles en cada paso, y si resuelve el problema en cualquiera de estas ramas, se dice que ha resuelto el problema. Claramente, este modelo no está destinado a ser un modelo físicamente realizable, es solo una máquina abstracta teóricamente interesante que da lugar a clases de complejidad particularmente interesantes. Para ver ejemplos, consulte algoritmo no determinista .
Otros modelos de máquinas
En la literatura se han propuesto muchos modelos de máquinas diferentes de las máquinas de Turing multicinta estándar, por ejemplo, las máquinas de acceso aleatorio . Tal vez sea sorprendente que cada uno de estos modelos se pueda convertir en otro sin proporcionar ninguna potencia computacional adicional. El consumo de tiempo y memoria de estos modelos alternativos puede variar. [2] Lo que todos estos modelos tienen en común es que las máquinas funcionan de manera determinista .
Sin embargo, algunos problemas computacionales son más fáciles de analizar en términos de recursos más inusuales. Por ejemplo, una máquina de Turing no determinista es un modelo computacional al que se le permite ramificarse para verificar muchas posibilidades diferentes a la vez. La máquina de Turing no determinista tiene muy poco que ver con la forma en que físicamente queremos calcular los algoritmos, pero su ramificación captura exactamente muchos de los modelos matemáticos que queremos analizar, de modo que el tiempo no determinista es un recurso muy importante para analizar problemas computacionales.
Medidas de complejidad
Para una definición precisa de lo que significa resolver un problema utilizando una cantidad dada de tiempo y espacio, se utiliza un modelo computacional como la máquina de Turing determinista . El tiempo requerido por una máquina de Turing determinista en la entrada es el número total de transiciones de estado, o pasos, que la máquina realiza antes de detenerse y emitir la respuesta ("sí" o "no"). Se dice que una máquina de Turing opera dentro del tiempo si el tiempo requerido por en cada entrada de longitud es como máximo . Un problema de decisión se puede resolver en el tiempo si existe una máquina de Turing que opera en el tiempo que resuelve el problema. Dado que la teoría de la complejidad está interesada en clasificar los problemas en función de su dificultad, se definen conjuntos de problemas en función de algunos criterios. Por ejemplo, el conjunto de problemas solucionables dentro del tiempo en una máquina de Turing determinista se denota por DTIME ( ).
Se pueden hacer definiciones análogas para los requisitos de espacio. Aunque el tiempo y el espacio son los recursos de complejidad más conocidos, cualquier medida de complejidad puede considerarse un recurso computacional. Las medidas de complejidad se definen de manera muy general mediante los axiomas de complejidad de Blum . Otras medidas de complejidad utilizadas en la teoría de la complejidad incluyen la complejidad de la comunicación , la complejidad del circuito y la complejidad del árbol de decisiones .
La complejidad de un algoritmo a menudo se expresa utilizando la notación O grande .
Complejidad del caso mejor, peor y promedio
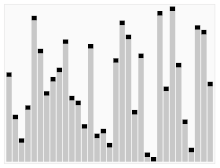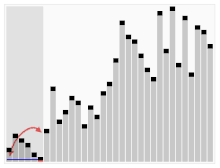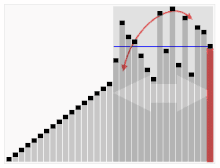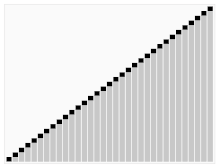
La complejidad del mejor, peor y promedio de los casos se refiere a tres formas diferentes de medir la complejidad temporal (o cualquier otra medida de complejidad) de diferentes entradas del mismo tamaño. Dado que algunas entradas de tamaño pueden ser más rápidas de resolver que otras, definimos las siguientes complejidades:
- Complejidad del mejor caso: es la complejidad de resolver el problema para la mejor entrada de tamaño .
- Complejidad del caso promedio: es la complejidad de resolver el problema en promedio. Esta complejidad solo se define con respecto a una distribución de probabilidad sobre las entradas. Por ejemplo, si se supone que todas las entradas del mismo tamaño tienen la misma probabilidad de aparecer, la complejidad del caso promedio se puede definir con respecto a la distribución uniforme sobre todas las entradas de tamaño .
- Análisis amortizado : el análisis amortizado considera tanto las operaciones costosas como las menos costosas juntas a lo largo de toda la serie de operaciones del algoritmo.
- Complejidad del peor caso: es la complejidad de resolver el problema para la peor entrada de tamaño .
El orden de más barato a más costoso es: Mejor, promedio (de distribución uniforme discreta ), amortizado, peor.
Por ejemplo, el algoritmo de ordenamiento determinista quicksort aborda el problema de ordenar una lista de números enteros. El peor de los casos es cuando el pivote es siempre el valor más grande o más pequeño de la lista (por lo que la lista nunca se divide). En este caso, el algoritmo tarda un tiempo O ( ). Si suponemos que todas las permutaciones posibles de la lista de entrada son igualmente probables, el tiempo medio que tarda la ordenación es . El mejor caso se produce cuando cada pivote divide la lista por la mitad, lo que también requiere tiempo.
Límites superior e inferior de la complejidad de los problemas
Para clasificar el tiempo de cálculo (o recursos similares, como el consumo de espacio), resulta útil demostrar límites superiores e inferiores sobre la cantidad máxima de tiempo requerida por el algoritmo más eficiente para resolver un problema dado. La complejidad de un algoritmo suele tomarse como su complejidad en el peor de los casos, a menos que se especifique lo contrario. El análisis de un algoritmo en particular cae dentro del campo del análisis de algoritmos . Para mostrar un límite superior sobre la complejidad temporal de un problema, uno necesita demostrar solamente que hay un algoritmo particular con un tiempo de ejecución como máximo de . Sin embargo, demostrar límites inferiores es mucho más difícil, ya que los límites inferiores hacen una declaración sobre todos los algoritmos posibles que resuelven un problema dado. La frase "todos los algoritmos posibles" incluye no solo los algoritmos conocidos hoy, sino cualquier algoritmo que pueda descubrirse en el futuro. Para mostrar un límite inferior de para un problema se requiere demostrar que ningún algoritmo puede tener una complejidad temporal menor que .
Los límites superiores e inferiores se suelen indicar utilizando la notación O mayúscula , que oculta los factores constantes y los términos más pequeños. Esto hace que los límites sean independientes de los detalles específicos del modelo computacional utilizado. Por ejemplo, si , en la notación O mayúscula se escribiría .
Clases de complejidad
Definición de clases de complejidad
Una clase de complejidad es un conjunto de problemas de complejidad relacionada. Las clases de complejidad más simples se definen por los siguientes factores:
- Tipo de problema computacional: Los problemas más utilizados son los de decisión. Sin embargo, se pueden definir clases de complejidad en función de problemas de funciones , problemas de conteo , problemas de optimización , problemas de promesa , etc.
- El modelo de computación: El modelo de computación más común es la máquina de Turing determinista, pero muchas clases de complejidad se basan en máquinas de Turing no deterministas, circuitos booleanos , máquinas de Turing cuánticas , circuitos monótonos , etc.
- El recurso (o recursos) que se está acotando y el límite: estas dos propiedades generalmente se expresan juntas, como "tiempo polinomial", "espacio logarítmico", "profundidad constante", etc.
Algunas clases de complejidad tienen definiciones complicadas que no encajan en este marco. Por lo tanto, una clase de complejidad típica tiene una definición como la siguiente:
- El conjunto de problemas de decisión que una máquina de Turing determinista puede resolver en un tiempo determinado . (Esta clase de complejidad se conoce como DTIME( )).
Pero limitar el tiempo de cálculo anterior mediante alguna función concreta a menudo produce clases de complejidad que dependen del modelo de máquina elegido. Por ejemplo, el lenguaje se puede resolver en tiempo lineal en una máquina de Turing de múltiples cintas, pero requiere necesariamente tiempo cuadrático en el modelo de máquinas de Turing de una sola cinta. Si permitimos variaciones polinómicas en el tiempo de ejecución, la tesis de Cobham-Edmonds afirma que "las complejidades temporales en dos modelos de cálculo razonables y generales cualesquiera están relacionadas polinómicamente" (Goldreich 2008, Capítulo 1.2). Esto forma la base para la clase de complejidad P , que es el conjunto de problemas de decisión que se pueden resolver mediante una máquina de Turing determinista dentro de un tiempo polinómico. El conjunto correspondiente de problemas de función es FP .
Clases de complejidad importantes
Se pueden definir muchas clases de complejidad importantes limitando el tiempo o el espacio que utiliza el algoritmo. Algunas clases de complejidad importantes de problemas de decisión definidos de esta manera son las siguientes:
| Recurso | Determinismo | Clase de complejidad | Restricción de recursos |
|---|---|---|---|
| Espacio | No determinista | Espacio Nacional ( ) | |
| ES | |||
| ESPACIO NP | |||
| ESPACIO NEXPOSITIVO | |||
| Determinista | Espacio D ( ) | ||
| yo | |||
| Espacio de pago | |||
| EXPESPACIO | |||
| Tiempo | No determinista | TIEMPONTOMETRO ( ) | |
| notario público | |||
| PRÓXIMA HORA | |||
| Determinista | TIEMPO DT ( ) | ||
| PAG | |||
| TIEMPO EXPERIMENTAL |
Las clases de espacio logarítmico no tienen en cuenta el espacio necesario para representar el problema.
Resulta que PSPACE = NPSPACE y EXPSPACE = NEXPSPACE según el teorema de Savitch .
Otras clases de complejidad importantes incluyen BPP , ZPP y RP , que se definen utilizando máquinas de Turing probabilísticas ; AC y NC , que se definen utilizando circuitos booleanos; y BQP y QMA , que se definen utilizando máquinas de Turing cuánticas. #P es una clase de complejidad importante de problemas de conteo (no problemas de decisión). Clases como IP y AM se definen utilizando sistemas de prueba interactivos . ALL es la clase de todos los problemas de decisión.
Teoremas de jerarquía
Para las clases de complejidad definidas de esta manera, es deseable probar que relajar los requisitos sobre (por ejemplo) el tiempo de cálculo de hecho define un conjunto mayor de problemas. En particular, aunque DTIME( ) está contenido en DTIME( ), sería interesante saber si la inclusión es estricta. Para los requisitos de tiempo y espacio, la respuesta a tales preguntas está dada por los teoremas de jerarquía de tiempo y espacio respectivamente. Se denominan teoremas de jerarquía porque inducen una jerarquía adecuada en las clases definidas al restringir los recursos respectivos. Por lo tanto, hay pares de clases de complejidad tales que una está incluida adecuadamente en la otra. Habiendo deducido tales inclusiones adecuadas en el conjunto, podemos proceder a hacer afirmaciones cuantitativas sobre cuánto tiempo o espacio adicional se necesita para aumentar el número de problemas que se pueden resolver.
Más precisamente, el teorema de jerarquía temporal establece que .
El teorema de jerarquía espacial establece que .
Los teoremas de jerarquía temporal y espacial forman la base de la mayoría de los resultados de separación de clases de complejidad. Por ejemplo, el teorema de jerarquía temporal nos dice que P está estrictamente contenido en EXPTIME, y el teorema de jerarquía espacial nos dice que L está estrictamente contenido en PSPACE.
Reducción
Muchas clases de complejidad se definen utilizando el concepto de reducción. Una reducción es una transformación de un problema en otro problema. Capta la noción informal de que un problema es, como máximo, tan difícil como otro problema. Por ejemplo, si un problema se puede resolver utilizando un algoritmo para , no es más difícil que , y decimos que se reduce a . Hay muchos tipos diferentes de reducciones, basados en el método de reducción, como las reducciones de Cook, las reducciones de Karp y las reducciones de Levin, y el límite de la complejidad de las reducciones, como las reducciones de tiempo polinomial o las reducciones de espacio logarítmico .
La reducción más utilizada es la reducción en tiempo polinómico. Esto significa que el proceso de reducción lleva tiempo polinómico. Por ejemplo, el problema de elevar al cuadrado un número entero se puede reducir al problema de multiplicar dos números enteros. Esto significa que se puede utilizar un algoritmo para multiplicar dos números enteros para elevar al cuadrado un número entero. De hecho, esto se puede hacer dando la misma entrada a ambas entradas del algoritmo de multiplicación. Así, vemos que elevar al cuadrado no es más difícil que multiplicar, ya que elevar al cuadrado se puede reducir a multiplicación.
Esto motiva el concepto de que un problema es difícil para una clase de complejidad. Un problema es difícil para una clase de problemas si cada problema en puede reducirse a . Por lo tanto, ningún problema en es más difícil que , ya que un algoritmo para nos permite resolver cualquier problema en . La noción de problemas difíciles depende del tipo de reducción que se utilice. Para clases de complejidad mayores que P, se utilizan comúnmente reducciones de tiempo polinomial. En particular, el conjunto de problemas que son difíciles para NP es el conjunto de problemas NP-difíciles .
Si un problema está en y es difícil para , entonces se dice que es completo para . Esto significa que es el problema más difícil en . (Dado que muchos problemas podrían ser igualmente difíciles, se podría decir que es uno de los problemas más difíciles en ). Por lo tanto, la clase de problemas NP-completos contiene los problemas más difíciles en NP, en el sentido de que son los que tienen más probabilidades de no estar en P. Debido a que el problema P = NP no está resuelto, ser capaz de reducir un problema NP-completo conocido, , a otro problema, , indicaría que no hay una solución en tiempo polinomial conocida para . Esto se debe a que una solución en tiempo polinomial para produciría una solución en tiempo polinomial para . De manera similar, debido a que todos los problemas NP se pueden reducir al conjunto, encontrar un problema NP-completo que se pueda resolver en tiempo polinomial significaría que P = NP. [3]
Problemas importantes abiertos
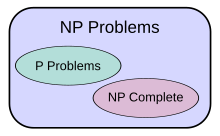
Problema P versus NP
La clase de complejidad P se considera a menudo como una abstracción matemática que modela aquellas tareas computacionales que admiten un algoritmo eficiente. Esta hipótesis se denomina tesis de Cobham-Edmonds . La clase de complejidad NP , por otro lado, contiene muchos problemas que a la gente le gustaría resolver de manera eficiente, pero para los cuales no se conoce ningún algoritmo eficiente, como el problema de satisfacibilidad booleano , el problema de la trayectoria hamiltoniana y el problema de cobertura de vértices . Dado que las máquinas de Turing deterministas son máquinas de Turing no deterministas especiales, se observa fácilmente que cada problema en P también es miembro de la clase NP.
La cuestión de si P es igual a NP es una de las cuestiones abiertas más importantes en la informática teórica debido a las amplias implicaciones de una solución. [3] Si la respuesta es sí, se puede demostrar que muchos problemas importantes tienen soluciones más eficientes. Estos incluyen varios tipos de problemas de programación entera en investigación de operaciones , muchos problemas en logística , predicción de la estructura de proteínas en biología , [5] y la capacidad de encontrar pruebas formales de teoremas de matemáticas puras . [6] El problema P versus NP es uno de los problemas del Premio del Milenio propuestos por el Instituto de Matemáticas Clay . Hay un premio de US$1,000,000 para resolver el problema. [7]
Problemas en NP que no se sabe que estén en P o NP-completos
Ladner demostró que si entonces existen problemas en que no son ni incompletos ni -completos. [4] Tales problemas se denominan problemas NP-intermedios . El problema del isomorfismo de grafos , el problema del logaritmo discreto y el problema de factorización de enteros son ejemplos de problemas que se cree que son NP-intermedios. Son algunos de los pocos problemas NP que no se sabe que sean incompletos ni -completos.
El problema del isomorfismo de grafos es el problema computacional de determinar si dos grafos finitos son isomorfos . Un importante problema sin resolver en la teoría de la complejidad es si el problema del isomorfismo de grafos es en , -completo o NP-intermedio. La respuesta no se conoce, pero se cree que el problema al menos no es NP-completo. [8] Si el isomorfismo de grafos es NP-completo, la jerarquía de tiempo polinomial colapsa a su segundo nivel. [9] Dado que se cree ampliamente que la jerarquía polinomial no colapsa a ningún nivel finito, se cree que el isomorfismo de grafos no es NP-completo. El mejor algoritmo para este problema, debido a László Babai y Eugene Luks, ha sido el tiempo de ejecución para grafos con vértices, aunque algunos trabajos recientes de Babai ofrecen algunas perspectivas potencialmente nuevas sobre esto. [10]
El problema de factorización de enteros es el problema computacional de determinar la factorización prima de un entero dado. Expresado como un problema de decisión, es el problema de decidir si la entrada tiene un factor primo menor que . No se conoce ningún algoritmo de factorización de enteros eficiente, y este hecho forma la base de varios sistemas criptográficos modernos, como el algoritmo RSA . El problema de factorización de enteros está en y en (e incluso en UP y co-UP [11] ). Si el problema es -completo, la jerarquía de tiempo polinomial colapsará a su primer nivel (es decir, será igual a ). El algoritmo más conocido para la factorización de enteros es el tamiz de campo numérico general , que toma tiempo [12] para factorizar un entero impar . Sin embargo, el algoritmo cuántico más conocido para este problema, el algoritmo de Shor , se ejecuta en tiempo polinomial. Desafortunadamente, este hecho no dice mucho sobre dónde radica el problema con respecto a las clases de complejidad no cuántica.
Separaciones entre otras clases de complejidad
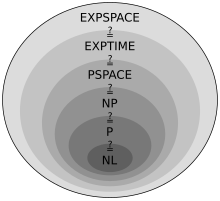
Se sospecha que muchas clases de complejidad conocidas son desiguales, pero esto no se ha demostrado. Por ejemplo , pero es posible que . Si no es igual a , entonces no es igual a ninguno de los dos. Dado que existen muchas clases de complejidad conocidas entre y , como , , , , , , etc., es posible que todas estas clases de complejidad se colapsen en una sola clase. Probar que cualquiera de estas clases es desigual sería un gran avance en la teoría de la complejidad.
En la misma línea, está la clase que contiene los problemas complementarios (es decir, problemas con las respuestas sí / no invertidas) de problemas. Se cree [13] que no es igual a ; sin embargo, aún no se ha demostrado. Está claro que si estas dos clases de complejidad no son iguales, entonces no es igual a , ya que . Por lo tanto, si tendríamos de donde .
De manera similar, no se sabe si (el conjunto de todos los problemas que se pueden resolver en el espacio logarítmico) está estrictamente contenido en o es igual a . Nuevamente, hay muchas clases de complejidad entre los dos, como y , y no se sabe si son clases distintas o iguales.
Se sospecha que y son iguales. Sin embargo, actualmente está abierto si .
Dificultad
Un problema que teóricamente puede resolverse, pero que requiere recursos imprácticos y finitos (por ejemplo, tiempo) para hacerlo, se conoce comoproblema intratable .[14]Por el contrario, un problema que se puede resolver en la práctica se denominaProblema manejable , literalmente "un problema que se puede manejar". El términoinviable(literalmente "no se puede hacer") a veces se usa indistintamente conintratable,[15]aunque esto conlleva el riesgo de confusión con unasolución factibleenoptimización matemática.[16]
Los problemas tratables se identifican frecuentemente con problemas que tienen soluciones en tiempo polinomial ( , ); esto se conoce como la tesis de Cobham–Edmonds . Los problemas que se sabe que son intratables en este sentido incluyen aquellos que son EXPTIME -hard. Si no es lo mismo que , entonces los problemas NP-hard también son intratables en este sentido.
Sin embargo, esta identificación es inexacta: una solución en tiempo polinomial con un grado grande o un coeficiente principal grande crece rápidamente y puede ser poco práctica para problemas de tamaño práctico; por el contrario, una solución en tiempo exponencial que crece lentamente puede ser práctica en una entrada realista, o una solución que toma mucho tiempo en el peor de los casos puede tomar poco tiempo en la mayoría de los casos o en el caso promedio, y por lo tanto aún ser práctica. Decir que un problema no está en no implica que todos los casos grandes del problema sean difíciles o incluso que la mayoría de ellos lo sean. Por ejemplo, se ha demostrado que el problema de decisión en la aritmética de Presburger no está en , pero se han escrito algoritmos que resuelven el problema en tiempos razonables en la mayoría de los casos. De manera similar, los algoritmos pueden resolver el problema de la mochila NP-completo en un amplio rango de tamaños en un tiempo menor que el cuadrático y los solucionadores SAT manejan rutinariamente grandes instancias del problema de satisfacibilidad booleana NP-completo .
Para ver por qué los algoritmos de tiempo exponencial son generalmente inutilizables en la práctica, considere un programa que realiza operaciones antes de detenerse. Para un número pequeño , digamos 100, y suponiendo a modo de ejemplo que la computadora realiza operaciones cada segundo, el programa se ejecutaría durante aproximadamente años, que es el mismo orden de magnitud que la edad del universo . Incluso con una computadora mucho más rápida, el programa solo sería útil para casos muy pequeños y, en ese sentido, la intratabilidad de un problema es algo independiente del progreso tecnológico. Sin embargo, un algoritmo de tiempo exponencial que realiza operaciones es práctico hasta que se vuelve relativamente grande.
De manera similar, un algoritmo de tiempo polinómico no siempre es práctico. Si su tiempo de ejecución es, por ejemplo, , no es razonable considerarlo eficiente y sigue siendo inútil excepto en casos pequeños. De hecho, en la práctica, incluso los algoritmos o suelen ser poco prácticos en problemas de tamaño realista.
Teoría de la complejidad continua
La teoría de la complejidad continua puede referirse a la teoría de la complejidad de problemas que involucran funciones continuas que se aproximan mediante discretizaciones, como se estudia en el análisis numérico . Un enfoque de la teoría de la complejidad del análisis numérico [17] es la complejidad basada en la información .
La teoría de la complejidad continua también puede referirse a la teoría de la complejidad del uso de computación analógica , que utiliza sistemas dinámicos continuos y ecuaciones diferenciales . [18] La teoría de control puede considerarse una forma de computación y las ecuaciones diferenciales se utilizan en el modelado de sistemas de tiempo continuo e híbridos de tiempo discreto-continuo. [19]
Historia
Un ejemplo temprano de análisis de complejidad de algoritmos es el análisis del tiempo de ejecución del algoritmo euclidiano realizado por Gabriel Lamé en 1844.
Antes de que se iniciara la investigación propiamente dicha dedicada a la complejidad de los problemas algorítmicos, varios investigadores habían establecido numerosas bases. La más influyente de ellas fue la definición de las máquinas de Turing de Alan Turing en 1936, que resultó ser una simplificación muy robusta y flexible de un ordenador.
El comienzo de los estudios sistemáticos en complejidad computacional se atribuye al artículo seminal de 1965 "Sobre la complejidad computacional de los algoritmos" de Juris Hartmanis y Richard E. Stearns , que estableció las definiciones de complejidad temporal y complejidad espacial , y demostró los teoremas de jerarquía. [20] Además, en 1965 Edmonds sugirió considerar un "buen" algoritmo como aquel con un tiempo de ejecución limitado por un polinomio del tamaño de entrada. [21]
Entre los trabajos anteriores que estudiaban problemas solucionables mediante máquinas de Turing con recursos acotados específicos se incluyen [20] la definición de autómatas lineales acotados de John Myhill (Myhill 1960), el estudio de los conjuntos rudimentarios de Raymond Smullyan (1961), así como el trabajo de Hisao Yamada [22] sobre cálculos en tiempo real (1962). Un poco antes, Boris Trakhtenbrot (1956), un pionero en el campo de la URSS, estudió otra medida de complejidad específica. [23] Como recuerda:
Sin embargo, mi interés inicial [en la teoría de autómatas] fue dejándose cada vez más de lado en favor de la complejidad computacional, una fusión apasionante de métodos combinatorios, heredados de la teoría de conmutación , con el arsenal conceptual de la teoría de algoritmos. Estas ideas se me habían ocurrido antes, en 1955, cuando acuñé el término "función de señalización", que hoy en día se conoce comúnmente como "medida de complejidad". [24]
En 1967, Manuel Blum formuló un conjunto de axiomas (ahora conocidos como axiomas de Blum ) que especifican propiedades deseables de las medidas de complejidad en el conjunto de funciones computables y demostró un resultado importante, el llamado teorema de aceleración . El campo comenzó a florecer en 1971 cuando Stephen Cook y Leonid Levin demostraron la existencia de problemas prácticamente relevantes que son NP-completos . En 1972, Richard Karp llevó esta idea un paso más allá con su artículo de referencia, "Reducibilidad entre problemas combinatorios", en el que demostró que 21 problemas combinatorios y teóricos de grafos diversos , cada uno famoso por su intratabilidad computacional, son NP-completos. [25]
Véase también
- Complejidad computacional
- Teoría de la complejidad descriptiva
- Complejidad del juego
- Lenguaje de las hojas
- Límites de computación
- Lista de clases de complejidad
- Lista de temas de computabilidad y complejidad
- Lista de problemas no resueltos en informática
- Complejidad parametrizada
- Complejidad de la prueba
- Teoría de la complejidad cuántica
- Teoría de la complejidad estructural
- Problema transcomputacional
- Complejidad computacional de operaciones matemáticas
Trabajos sobre la complejidad
- Wuppuluri, Shyam; Doria, Francisco A., eds. (2020), Desentrañando la complejidad: la vida y la obra de Gregory Chaitin, World Scientific, doi :10.1142/11270, ISBN 978-981-12-0006-9, Número de identificación del sujeto 198790362
Referencias
Citas
- ^ "Problema P vs NP | Clay Mathematics Institute" www.claymath.org . Archivado desde el original el 6 de julio de 2018 . Consultado el 6 de julio de 2018 .
- ^ Véase Arora y Barak 2009, Capítulo 1: El modelo computacional y por qué no importa
- ^ ab Véase Sipser 2006, Capítulo 7: Complejidad temporal
- ^ ab Ladner, Richard E. (1975), "Sobre la estructura de la reducibilidad temporal polinomial", Journal of the ACM , 22 (1): 151–171, doi : 10.1145/321864.321877 , S2CID 14352974.
- ^ Berger, Bonnie A. ; Leighton, T (1998), "El plegamiento de proteínas en el modelo hidrofóbico-hidrofílico (HP) es NP-completo", Journal of Computational Biology , 5 (1): 27–40, CiteSeerX 10.1.1.139.5547 , doi :10.1089/cmb.1998.5.27, PMID 9541869.
- ^ Cook, Stephen (abril de 2000), The P versus NP Problem (PDF) , Clay Mathematics Institute , archivado desde el original (PDF) el 12 de diciembre de 2010 , consultado el 18 de octubre de 2006 .
- ^ Jaffe, Arthur M. (2006), "El Gran Desafío del Milenio en Matemáticas" (PDF) , Avisos de la AMS , 53 (6), archivado (PDF) desde el original el 12 de junio de 2006 , consultado el 18 de octubre de 2006 .
- ^ Arvind, Vikraman; Kurur, Piyush P. (2006), "El isomorfismo de grafos está en SPP", Información y Computación , 204 (5): 835–852, doi :10.1016/j.ic.2006.02.002.
- ^ Schöning, Uwe (1988), "El isomorfismo de grafos está en la jerarquía baja", Journal of Computer and System Sciences , 37 (3): 312–323, doi :10.1016/0022-0000(88)90010-4
- ^ Babai, László (2016). "Isomorfismo gráfico en tiempo cuasipolinomial". arXiv : 1512.03547 [cs.DS].
- ^ Fortnow, Lance (13 de septiembre de 2002). "Blog sobre complejidad computacional: factorización". weblog.fortnow.com .
- ^ Wolfram MathWorld: Tamiz de campos numéricos
- ^ Curso de Boaz Barak sobre complejidad computacional Lección 2
- ^ Hopcroft, JE, Motwani, R. y Ullman, JD (2007) Introducción a la teoría de autómatas, lenguajes y computación , Addison Wesley, Boston/San Francisco/Nueva York (página 368)
- ^ Meurant, Gerard (2014). Algoritmos y Complejidad . Elsevier. pag. pag. 4.ISBN 978-0-08093391-7.
- ^ Zobel, Justin (2015). Escritura para la informática . Springer. pág. 132. ISBN 978-1-44716639-9.
- ^ Smale, Steve (1997). "Teoría de la complejidad y análisis numérico". Acta Numerica . 6 . Cambridge Univ Press: 523–551. Bibcode :1997AcNum...6..523S. CiteSeerX 10.1.1.33.4678 . doi :10.1017/s0962492900002774. S2CID 5949193.
- ^ Babai, László; Campagnolo, Manuel (2009). "Una encuesta sobre cálculos de tiempo continuo". arXiv : 0907.3117 [cs.CC].
- ^ Tomlin, Claire J.; Mitchell, Ian; Bayen, Alexandre M.; Oishi, Meeko (julio de 2003). "Técnicas computacionales para la verificación de sistemas híbridos". Actas del IEEE . 91 (7): 986–1001. CiteSeerX 10.1.1.70.4296 . doi :10.1109/jproc.2003.814621.
- ^ de Fortnow y Homer (2003)
- ^ Richard M. Karp, "Combinatoria, complejidad y aleatoriedad", conferencia del premio Turing de 1985
- ^ Yamada, H. (1962). "Computación en tiempo real y funciones recursivas no computables en tiempo real". IEEE Transactions on Electronic Computers . EC-11 (6): 753–760. doi :10.1109/TEC.1962.5219459.
- ^ Trakhtenbrot, BA: Funciones de señalización y operadores tabulares. Uchionnye Zapiski Penzenskogo Pedinstituta (Transacciones del Instituto Pedagógico de Penza) 4, 75–87 (1956) (en ruso)
- ^ Boris Trakhtenbrot, "De la lógica a la informática teórica: una actualización". En: Pillars of Computer Science , LNCS 4800, Springer 2008.
- ^ Richard M. Karp (1972), "Reducibility Among Combinatorial Problems" (PDF) , en RE Miller; JW Thatcher (eds.), Complexity of Computer Computations , Nueva York: Plenum, pp. 85–103, archivado desde el original (PDF) el 29 de junio de 2011 , consultado el 28 de septiembre de 2009
Libros de texto
- Arora, Sanjeev ; Barak, Boaz (2009), Complejidad computacional: un enfoque moderno, Cambridge University Press, ISBN 978-0-521-42426-4, Zbl1193.68112
- Downey, Rod; Fellows, Michael (1999), Complejidad parametrizada , Monografías en Ciencias de la Computación, Berlín, Nueva York: Springer-Verlag, ISBN 9780387948836
- Du, Ding-Zhu; Ko, Ker-I (2000), Teoría de la complejidad computacional , John Wiley & Sons, ISBN 978-0-471-34506-0
- Garey, Michael R. ; Johnson, David S. (1979). Computadoras e intratabilidad: una guía para la teoría de la NP-completitud . Serie de libros sobre ciencias matemáticas (1.ª ed.). Nueva York: WH Freeman and Company . ISBN 9780716710455. Sr. 0519066. OCLC 247570676.
- Goldreich, Oded (2008), Complejidad computacional: una perspectiva conceptual, Cambridge University Press
- van Leeuwen, Jan , ed. (1990), Manual de informática teórica (vol. A): algoritmos y complejidad , MIT Press, ISBN 978-0-444-88071-0
- Papadimitriou, Christos (1994), Complejidad computacional (1.ª ed.), Addison Wesley, ISBN 978-0-201-53082-7
- Sipser, Michael (2006), Introducción a la teoría de la computación (2.ª ed.), EE. UU.: Thomson Course Technology, ISBN 978-0-534-95097-2
Encuestas
- Khalil, Hatem; Ulery, Dana (1976), "Una revisión de los estudios actuales sobre la complejidad de los algoritmos para ecuaciones diferenciales parciales", Actas de la conferencia anual sobre - ACM 76, págs. 197-201, doi :10.1145/800191.805573, ISBN 9781450374897, Número de identificación del sujeto 15497394
- Cook, Stephen (1983), "Una visión general de la complejidad computacional", Communications of the ACM , 26 (6): 400–408, doi : 10.1145/358141.358144 , ISSN 0001-0782, S2CID 14323396
- Fortnow, Lance; Homer, Steven (2003), "Una breve historia de la complejidad computacional" (PDF) , Boletín de la EATCS , 80 : 95–133
- Mertens, Stephan (2002), "Complejidad computacional para físicos", Computing in Science & Engineering , 4 (3): 31–47, arXiv : cond-mat/0012185 , Bibcode :2002CSE.....4c..31M, doi :10.1109/5992.998639, ISSN 1521-9615, S2CID 633346
Enlaces externos
- El Zoológico de la Complejidad
- "Clases de complejidad computacional", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
- Scott Aaronson: Por qué los filósofos deberían preocuparse por la complejidad computacional
































![{\displaystyle O(e^{\left({\sqrt[{3}]{\frac {64}{9}}}\right){\sqrt[{3}]{(\log n)}}{\sqrt[{3}]{(\log \log n)^{2}}}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d50912fbf223d0bbadd2a028262414397fbee1a9)

























