Paridad de cero

En matemáticas, el cero es un número par . En otras palabras, su paridad —la cualidad de un entero de ser par o impar— es par. Esto se puede verificar fácilmente con base en la definición de "par": cero es un múltiplo entero de 2 , específicamente 0 × 2. Como resultado, cero comparte todas las propiedades que caracterizan a los números pares: por ejemplo, 0 tiene como vecinos en ambos lados a números impares, cualquier entero decimal tiene la misma paridad que su último dígito —por lo tanto, como 10 es par, 0 será par, y si y es par entonces y + x tiene la misma paridad que x —de hecho, 0 + x y x siempre tienen la misma paridad.
El cero también encaja en los patrones formados por otros números pares. Las reglas de paridad de la aritmética, como por ejemplo par − par = par , requieren que el 0 sea par. El cero es el elemento identidad aditivo del grupo de los números enteros pares, y es el caso de partida a partir del cual se definen recursivamente otros números naturales pares . Las aplicaciones de esta recursión desde la teoría de grafos a la geometría computacional se basan en que el cero sea par. El 0 no solo es divisible por 2, sino que es divisible por cada potencia de 2 , lo que es relevante para el sistema de numeración binario utilizado por las computadoras. En este sentido, el 0 es el número "más par" de todos. [1]
Entre el público en general, la paridad del cero puede ser una fuente de confusión. En los experimentos de tiempo de reacción , la mayoría de las personas son más lentas en identificar el 0 como par que el 2, el 4, el 6 o el 8. Algunos profesores (y algunos niños en clases de matemáticas) piensan que el cero es impar, o que es par e impar, o que no es ni lo uno ni lo otro. Los investigadores en educación matemática proponen que estos conceptos erróneos pueden convertirse en oportunidades de aprendizaje. El estudio de igualdades como 0 × 2 = 0 puede abordar las dudas de los estudiantes sobre llamar al 0 un número y usarlo en aritmética . Los debates en clase pueden llevar a los estudiantes a apreciar los principios básicos del razonamiento matemático, como la importancia de las definiciones. La evaluación de la paridad de este número excepcional es un ejemplo temprano de un tema omnipresente en las matemáticas: la abstracción de un concepto familiar a un entorno desconocido.
¿Por qué el cero es par?
La definición estándar de "número par" se puede utilizar para demostrar directamente que cero es par. Un número se llama "par" si es un múltiplo entero de 2. Por ejemplo, la razón por la que 10 es par es que es igual a 5 × 2. De la misma manera, cero es un múltiplo entero de 2, es decir, 0 × 2, por lo que cero es par. [2]
También es posible explicar por qué el cero es par sin recurrir a definiciones formales. [3] Las siguientes explicaciones dan sentido a la idea de que el cero es par en términos de conceptos numéricos fundamentales. A partir de esta base, se puede proporcionar una justificación para la definición en sí y su aplicabilidad al cero.
Explicaciones básicas

Dado un conjunto de objetos, se utiliza un número para describir cuántos objetos hay en el conjunto. Cero es el recuento de ningún objeto ; en términos más formales, es el número de objetos en el conjunto vacío . El concepto de paridad se utiliza para hacer grupos de dos objetos. Si los objetos de un conjunto se pueden marcar en grupos de dos, sin que quede ninguno, entonces el número de objetos es par. Si queda un objeto, entonces el número de objetos es impar. El conjunto vacío contiene cero grupos de dos, y no queda ningún objeto de esta agrupación, por lo que cero es par. [5]
Estas ideas se pueden ilustrar dibujando objetos en pares. Es difícil representar grupos de dos con cero objetos o enfatizar la inexistencia de un objeto sobrante, por lo que resulta útil dibujar otras agrupaciones y compararlas con cero. Por ejemplo, en el grupo de cinco objetos, hay dos pares. Más importante aún, hay un objeto sobrante, por lo que 5 es impar. En el grupo de cuatro objetos, no hay ningún objeto sobrante, por lo que 4 es par. En el grupo de un solo objeto, no hay pares y hay un objeto sobrante, por lo que 1 es impar. En el grupo de cero objetos, no hay ningún objeto sobrante, por lo que 0 es par. [6]
Existe otra definición concreta de uniformidad: si los objetos de un conjunto pueden colocarse en dos grupos de igual tamaño, entonces el número de objetos es par. Esta definición es equivalente a la primera. Nuevamente, cero es par porque el conjunto vacío puede dividirse en dos grupos de cero elementos cada uno. [7]
Los números también se pueden visualizar como puntos en una línea numérica . Cuando se distinguen entre sí los números pares e impares, su patrón se hace evidente, especialmente si se incluyen números negativos:

Los números pares e impares se alternan. Partiendo de cualquier número par, contando hacia arriba o hacia abajo de dos en dos se llega a los demás números pares, y no hay razón para saltarse el cero. [8]
Con la introducción de la multiplicación , la paridad puede abordarse de una manera más formal utilizando expresiones aritméticas. Cada número entero tiene la forma (2 × ▢) + 0 o (2 × ▢) + 1; los primeros números son pares y los segundos son impares. Por ejemplo, 1 es impar porque 1 = (2 × 0) + 1, y 0 es par porque 0 = (2 × 0) + 0. Hacer una tabla de estos hechos refuerza la imagen de la línea numérica anterior. [9]
Definición de paridad
La definición precisa de un término matemático, como "par", que significa "múltiplo entero de dos", es en última instancia una convención . A diferencia de "par", algunos términos matemáticos se construyen a propósito para excluir casos triviales o degenerados . Los números primos son un ejemplo famoso. Antes del siglo XX, las definiciones de primalidad eran inconsistentes, y matemáticos importantes como Goldbach , Lambert , Legendre , Cayley y Kronecker escribieron que 1 era primo. [10] La definición moderna de "número primo" es "entero positivo con exactamente 2 factores ", por lo que 1 no es primo. Esta definición se puede racionalizar observando que se adapta de manera más natural a los teoremas matemáticos que se refieren a los primos. Por ejemplo, el teorema fundamental de la aritmética es más fácil de enunciar cuando 1 no se considera primo. [11]
Sería posible redefinir de manera similar el término "par" de manera que ya no incluya el cero. Sin embargo, en este caso, la nueva definición dificultaría el enunciado de teoremas relativos a los números pares. El efecto ya se puede ver en las reglas algebraicas que rigen los números pares e impares . [12] Las reglas más relevantes se refieren a la suma , la resta y la multiplicación :
- par ± par = par
- impar ± impar = par
- par × entero = par
Insertando valores apropiados en los lados izquierdos de estas reglas, se puede producir 0 en los lados derechos:
- 2 − 2 = 0
- -3 + 3 = 0
- 4 × 0 = 0
Por lo tanto, las reglas anteriores serían incorrectas si el cero no fuera par. [12] En el mejor de los casos, habría que modificarlas. Por ejemplo, una guía de estudio para exámenes afirma que los números pares se caracterizan como múltiplos enteros de dos, pero el cero no es "ni par ni impar". [13] En consecuencia, las reglas de la guía para números pares e impares contienen excepciones:
- par ± par = par (o cero)
- impar ± impar = par (o cero)
- par × entero distinto de cero = par [13]
Hacer una excepción para el cero en la definición de paridad obliga a hacer tales excepciones en las reglas para los números pares. Desde otra perspectiva, tomar las reglas que obedecen los números pares positivos y exigir que sigan siendo válidas para los números enteros obliga a la definición habitual y a la paridad del cero. [12]
Contextos matemáticos
Innumerables resultados en teoría de números invocan el teorema fundamental de la aritmética y las propiedades algebraicas de los números pares, por lo que las opciones anteriores tienen consecuencias de largo alcance. Por ejemplo, el hecho de que los números positivos tengan factorizaciones únicas significa que se puede determinar si un número tiene un número par o impar de factores primos distintos. Como 1 no es primo ni tiene factores primos, es un producto de 0 primos distintos; como 0 es un número par, 1 tiene un número par de factores primos distintos. Esto implica que la función de Möbius toma el valor μ(1) = 1 , que es necesario para que sea una función multiplicativa y para que funcione la fórmula de inversión de Möbius . [14]
No ser extraño
Un número n es impar si existe un entero k tal que n = 2 k + 1 . Una forma de demostrar que cero no es impar es por contradicción : si 0 = 2 k + 1 entonces k = −1/2 , que no es un entero. [15] Como cero no es impar, si se demuestra que un número desconocido es impar, entonces no puede ser cero. Esta observación aparentemente trivial puede proporcionar una prueba conveniente y reveladora que explica por qué un número impar es distinto de cero.
Un resultado clásico de la teoría de grafos establece que un grafo de orden impar (que tiene un número impar de vértices) siempre tiene al menos un vértice de grado par . (La afirmación en sí misma requiere que cero sea par: el grafo vacío tiene un orden par y un vértice aislado tiene un grado par.) [16] Para probar la afirmación, en realidad es más fácil probar un resultado más fuerte: cualquier grafo de orden impar tiene un número impar de vértices de grado par. La aparición de este número impar se explica por un resultado aún más general, conocido como el lema del apretón de manos : cualquier grafo tiene un número par de vértices de grado impar. [17] Finalmente, el número par de vértices impares se explica naturalmente por la fórmula de suma de grados .
El lema de Sperner es una aplicación más avanzada de la misma estrategia. El lema establece que un determinado tipo de coloración en una triangulación de un símplex tiene un subsímplex que contiene todos los colores. En lugar de construir directamente dicho subsímplex, es más conveniente demostrar que existe un número impar de tales subsímplex mediante un argumento de inducción . [18] Una formulación más contundente del lema explica entonces por qué este número es impar: se descompone naturalmente como ( n + 1) + n cuando se consideran las dos orientaciones posibles de un símplex. [19]
Alternancia par-impar
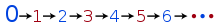
El hecho de que el cero sea par, junto con el hecho de que los números pares e impares se alternan, es suficiente para determinar la paridad de cualquier otro número natural . Esta idea se puede formalizar en una definición recursiva del conjunto de números naturales pares:
- 0 es par.
- ( n + 1) es par si y sólo si n no es par.
Esta definición tiene la ventaja conceptual de basarse únicamente en los fundamentos mínimos de los números naturales: la existencia del 0 y de los sucesores . Como tal, es útil para sistemas de lógica computacional como LF y el demostrador de teoremas de Isabelle . [20] Con esta definición, la paridad del cero no es un teorema sino un axioma. De hecho, "cero es un número par" puede interpretarse como uno de los axiomas de Peano , de los cuales los números naturales pares son un modelo. [21] Una construcción similar extiende la definición de paridad a los números ordinales transfinitos : todo ordinal límite es par, incluido el cero, y los sucesores de los ordinales pares son impares. [22]

La clásica prueba del punto en un polígono de la geometría computacional aplica las ideas anteriores. Para determinar si un punto se encuentra dentro de un polígono , se proyecta un rayo desde el infinito hasta el punto y se cuenta el número de veces que el rayo cruza el borde del polígono. El número de cruces es par si y solo si el punto está fuera del polígono. Este algoritmo funciona porque si el rayo nunca cruza el polígono, entonces su número de cruces es cero, que es par, y el punto está fuera. Cada vez que el rayo cruza el polígono, el número de cruces alterna entre par e impar, y el punto en su punta alterna entre exterior e interior. [23]

En teoría de grafos, un grafo bipartito es un grafo cuyos vértices están divididos en dos colores , de modo que los vértices vecinos tienen colores diferentes. Si un grafo conexo no tiene ciclos impares , entonces se puede construir una bipartición eligiendo un vértice base v y coloreando cada vértice de negro o blanco, dependiendo de si su distancia a v es par o impar. Dado que la distancia entre v y él mismo es 0, y 0 es par, el vértice base se colorea de manera diferente a sus vecinos, que se encuentran a una distancia de 1. [24]
Patrones algebraicos

En álgebra abstracta , los números enteros pares forman varias estructuras algebraicas que requieren la inclusión del cero. El hecho de que la identidad aditiva (cero) sea par, junto con la uniformidad de las sumas y los inversos aditivos de los números pares y la asociatividad de la adición, significa que los números enteros pares forman un grupo . Además, el grupo de números enteros pares bajo la adición es un subgrupo del grupo de todos los números enteros; este es un ejemplo elemental del concepto de subgrupo. [16] La observación anterior de que la regla "par − par = par" obliga a que 0 sea par es parte de un patrón general: cualquier subconjunto no vacío de un grupo aditivo que esté cerrado bajo la resta debe ser un subgrupo y, en particular, debe contener la identidad . [25]
Como los números enteros pares forman un subgrupo de los números enteros, dividen los números enteros en clases laterales . Estas clases laterales pueden describirse como las clases de equivalencia de la siguiente relación de equivalencia : x ~ y si ( x − y ) es par. Aquí, la paridad de cero se manifiesta directamente como la reflexividad de la relación binaria ~. [26] Solo hay dos clases laterales de este subgrupo (los números pares y los impares), por lo que tiene índice 2.
Análogamente, el grupo alternante es un subgrupo de índice 2 en el grupo simétrico de n letras. Los elementos del grupo alternante, llamados permutaciones pares , son los productos de números pares de transposiciones . La función identidad , un producto vacío de ninguna transposición, es una permutación par ya que cero es par; es el elemento identidad del grupo. [27]
La regla "par × entero = par" significa que los números pares forman un ideal en el anillo de los enteros, y la relación de equivalencia anterior puede describirse como equivalencia módulo este ideal . En particular, los enteros pares son exactamente aquellos enteros k donde k ≡ 0 (mod 2). Esta formulación es útil para investigar los ceros enteros de los polinomios . [28]
Orden 2-ádica
En cierto sentido, algunos múltiplos de 2 son "más pares" que otros. Los múltiplos de 4 se denominan doblemente pares , ya que pueden dividirse por 2 dos veces. El cero no solo es divisible por 4, sino que tiene la propiedad única de ser divisible por cada potencia de 2 , por lo que supera a todos los demás números en "paridad". [1]
Una consecuencia de este hecho aparece en el ordenamiento invertido de bits de los tipos de datos enteros que utilizan algunos algoritmos informáticos, como la transformada rápida de Fourier de Cooley-Tukey . Este ordenamiento tiene la propiedad de que cuanto más a la izquierda aparezca el primer 1 en la expansión binaria de un número , o cuantas más veces sea divisible por 2, más pronto aparecerá. La inversión de bits del cero sigue siendo cero; se puede dividir por 2 cualquier número de veces y su expansión binaria no contiene ningún 1, por lo que siempre aparece primero. [29]
Aunque 0 es divisible por 2 más veces que cualquier otro número, no es sencillo cuantificar exactamente cuántas veces lo es. Para cualquier entero distinto de cero n , se puede definir el orden 2-ádico de n como el número de veces que n es divisible por 2. Esta descripción no funciona para 0; no importa cuántas veces se divida por 2, siempre se puede dividir por 2 nuevamente. En cambio, la convención habitual es establecer el orden 2 de 0 como infinito como un caso especial. [30] Esta convención no es peculiar del orden 2; es uno de los axiomas de una valoración aditiva en álgebra superior. [31]
Las potencias de dos (1, 2, 4, 8, ...) forman una secuencia simple de números de orden 2 creciente. En los números 2-ádicos , tales secuencias convergen a cero. [32]
Educación

El tema de la paridad del cero se trata a menudo durante los dos o tres primeros años de educación primaria , cuando se introduce y desarrolla el concepto de números pares e impares. [34]
Conocimientos de los estudiantes
El gráfico de la derecha [33] muestra las creencias de los niños sobre la paridad del cero a medida que pasan del primer al sexto año del sistema educativo inglés . Los datos son de Len Frobisher, quien realizó un par de encuestas a escolares ingleses. Frobisher estaba interesado en cómo el conocimiento de la paridad de un solo dígito se traduce en el conocimiento de la paridad de varios dígitos, y el cero ocupa un lugar destacado en los resultados. [35]
En una encuesta preliminar de casi 400 niños de siete años, el 45% eligió par en lugar de impar cuando se les preguntó la paridad de cero. [36] Una investigación de seguimiento ofreció más opciones: ninguno , ambos y no sé . Esta vez, el número de niños en el mismo rango de edad que identificaron cero como par se redujo al 32%. [37] El éxito en decidir que cero es par inicialmente se dispara y luego se estabiliza en alrededor del 50% en los años 3 a 6. [38] A modo de comparación, la tarea más fácil, identificar la paridad de un solo dígito, se estabiliza en alrededor del 85% de éxito. [39]
En las entrevistas, Frobisher pidió a los estudiantes que razonaran. Un alumno de quinto año decidió que el 0 era par porque se encontraba en la tabla del 2. Un par de alumnos de cuarto año se dieron cuenta de que el cero se puede dividir en partes iguales. Otro alumno de cuarto año razonó "1 es impar y si voy hacia abajo es par". [40] Las entrevistas también revelaron los conceptos erróneos detrás de las respuestas incorrectas. Un alumno de segundo año estaba "bastante convencido" de que el cero era impar, sobre la base de que "es el primer número que se cuenta". [41] Un alumno de cuarto año se refirió al 0 como "ninguno" y pensó que no era ni par ni impar, ya que "no es un número". [42] En otro estudio, Annie Keith observó una clase de 15 alumnos de segundo grado que se convencían entre sí de que el cero era un número par basándose en la alternancia par-impar y en la posibilidad de dividir un grupo de cosas cero en dos grupos iguales. [43]
Esther Levenson, Pessia Tsamir y Dina Tirosh realizaron investigaciones más profundas, entrevistando a un par de estudiantes de sexto grado en los EE. UU. que tenían un alto rendimiento en su clase de matemáticas. Un estudiante prefería explicaciones deductivas de afirmaciones matemáticas, mientras que el otro prefería ejemplos prácticos. Ambos estudiantes pensaron inicialmente que el 0 no era ni par ni impar, por diferentes razones. Levenson et al. demostraron cómo el razonamiento de los estudiantes reflejaba sus conceptos de cero y división. [44]
| Reclamaciones realizadas por estudiantes [45] |
|---|
| " El cero no es par ni impar. " |
| " El cero podría ser par. " |
| " El cero no es impar. " |
| " El cero tiene que ser un número par. " |
| " El cero no es un número par. " |
| " El cero siempre será un número par " . |
| " El cero no siempre será un número par " . |
| " Cero es par. " |
| " El cero es especial. " |
Deborah Loewenberg Ball analizó las ideas de los estudiantes de tercer grado de Estados Unidos sobre los números pares e impares y el cero, que acababan de discutir con un grupo de estudiantes de cuarto grado. Los estudiantes discutieron la paridad del cero, las reglas para los números pares y cómo se hacen las matemáticas. Las afirmaciones sobre el cero tomaron muchas formas, como se ve en la lista de la derecha. [45] Ball y sus coautores argumentaron que el episodio demostró cómo los estudiantes pueden "hacer matemáticas en la escuela", en oposición a la reducción habitual de la disciplina a la solución mecánica de ejercicios. [46]
Uno de los temas de la literatura de investigación es la tensión entre las imágenes conceptuales de los estudiantes sobre la paridad y sus definiciones conceptuales. [47] Los estudiantes de sexto grado de Levenson et al. definieron los números pares como múltiplos de 2 o números divisibles por 2, pero inicialmente no pudieron aplicar esta definición al cero, porque no estaban seguros de cómo multiplicar o dividir cero por 2. El entrevistador finalmente los llevó a concluir que cero era par; los estudiantes tomaron diferentes caminos para llegar a esta conclusión, basándose en una combinación de imágenes, definiciones, explicaciones prácticas y explicaciones abstractas. En otro estudio, David Dickerson y Damien Pitman examinaron el uso de definiciones por parte de cinco estudiantes universitarios avanzados de matemáticas . Encontraron que los estudiantes universitarios eran en gran medida capaces de aplicar la definición de "par" al cero, pero aún no estaban convencidos de este razonamiento, ya que entraba en conflicto con sus imágenes conceptuales. [48]
Conocimientos de los profesores
Los investigadores de la educación matemática de la Universidad de Michigan han incluido la pregunta de verdadero o falso "0 es un número par" en una base de datos de más de 250 preguntas diseñadas para medir el conocimiento de los contenidos de los profesores. Para ellos, la pregunta ejemplifica el "conocimiento común... que cualquier adulto bien educado debería tener", y es "ideológicamente neutral" en el sentido de que la respuesta no varía entre las matemáticas tradicionales y las reformadas . En un estudio realizado entre 2000 y 2004 con 700 maestros de primaria en los Estados Unidos , el desempeño general en estas preguntas predijo significativamente mejoras en las puntuaciones de los estudiantes en las pruebas estandarizadas después de tomar las clases de los maestros. [49] En un estudio más profundo de 2008, los investigadores encontraron una escuela donde todos los maestros pensaban que el cero no era ni par ni impar, incluido un maestro que era ejemplar en todas las demás medidas. La idea errónea había sido difundida por un entrenador de matemáticas en su edificio. [50]
No se sabe con certeza cuántos profesores tienen ideas erróneas sobre el cero. Los estudios de Michigan no publicaron datos de preguntas individuales. Betty Lichtenberg, profesora adjunta de educación matemática en la Universidad del Sur de Florida , en un estudio de 1972 informó que cuando a un grupo de futuros maestros de escuela primaria se les dio una prueba de verdadero o falso que incluía la pregunta "El cero es un número par", encontraron que era una "pregunta difícil", y aproximadamente dos tercios respondieron "Falso". [51]
Implicaciones para la instrucción
Matemáticamente, demostrar que el cero es par es una cuestión sencilla de aplicar una definición, pero se necesita más explicación en el contexto de la educación. Una cuestión se refiere a los fundamentos de la prueba; la definición de "par" como "múltiplo entero de 2" no siempre es apropiada. Un estudiante en los primeros años de educación primaria puede no haber aprendido todavía qué significa "entero" o "múltiplo", mucho menos cómo multiplicar por 0. [52] Además, enunciar una definición de paridad para todos los números enteros puede parecer un atajo conceptual arbitrario si los únicos números pares investigados hasta ahora han sido positivos. Puede ser útil reconocer que, a medida que el concepto de número se extiende desde los números enteros positivos para incluir el cero y los números enteros negativos, las propiedades de los números como la paridad también se extienden de una manera no trivial. [53]
Cognición numérica

Los adultos que creen que el cero es par pueden, sin embargo, no estar familiarizados con el hecho de pensar en él como par, lo suficiente como para que se ralenticen considerablemente en un experimento de tiempo de reacción . Stanislas Dehaene , un pionero en el campo de la cognición numérica , dirigió una serie de experimentos de este tipo a principios de los años 1990. Se muestra un número al sujeto en un monitor y una computadora registra el tiempo que tarda el sujeto en presionar uno de dos botones para identificar el número como par o impar. Los resultados mostraron que el 0 era más lento de procesar que otros números pares. Algunas variaciones del experimento encontraron demoras de hasta 60 milisegundos o aproximadamente el 10% del tiempo de reacción promedio, una diferencia pequeña pero significativa. [55]
Los experimentos de Dehaene no fueron diseñados específicamente para investigar el 0, sino para comparar modelos competitivos de cómo se procesa y extrae la información de paridad. El modelo más específico, la hipótesis del cálculo mental, sugiere que las reacciones al 0 deberían ser rápidas; 0 es un número pequeño y es fácil calcular 0 × 2 = 0. (Se sabe que los sujetos calculan y nombran el resultado de la multiplicación por cero más rápido que la multiplicación de números distintos de cero, aunque son más lentos para verificar los resultados propuestos como 2 × 0 = 0. ) Los resultados de los experimentos sugirieron que estaba sucediendo algo bastante diferente: la información de paridad aparentemente se estaba recordando de la memoria junto con un grupo de propiedades relacionadas, como ser primo o una potencia de dos . Tanto la secuencia de potencias de dos como la secuencia de números pares positivos 2, 4, 6, 8, ... son categorías mentales bien diferenciadas cuyos miembros son prototípicamente pares. El cero no pertenece a ninguna de las listas, de ahí las respuestas más lentas. [56]
Experimentos repetidos han demostrado un retraso en el cero en sujetos de distintas edades y orígenes nacionales y lingüísticos, confrontados con nombres de números en forma numérica , deletreados y deletreados en una imagen especular. El grupo de Dehaene encontró un factor diferenciador: la pericia matemática. En uno de sus experimentos, los estudiantes de la École Normale Supérieure se dividieron en dos grupos: los de estudios literarios y los de matemáticas, física o biología. La desaceleración en el cero se encontró "esencialmente en el grupo [literario]", y de hecho, "antes del experimento, algunos sujetos L no estaban seguros de si el 0 era par o impar y tuvieron que recordarles la definición matemática". [57]
Esta fuerte dependencia de la familiaridad debilita nuevamente la hipótesis del cálculo mental. [58] El efecto también sugiere que es inadecuado incluir el cero en experimentos en los que se comparan números pares e impares como grupo. Como dice un estudio: "La mayoría de los investigadores parecen estar de acuerdo en que el cero no es un número par típico y no debería investigarse como parte de la línea numérica mental". [59]
Contextos cotidianos
Algunos de los contextos en los que aparece la paridad del cero son puramente retóricos. El lingüista Joseph Grimes reflexiona sobre la idea de que preguntar a las parejas casadas "¿Es el cero un número par?" es una buena manera de lograr que discrepen. [60] Las personas que piensan que el cero no es ni par ni impar pueden utilizar la paridad del cero como prueba de que cada regla tiene un contraejemplo , [61] o como ejemplo de una pregunta capciosa . [62]
Alrededor del año 2000, los medios de comunicación notaron un par de hitos inusuales: "19/11/1999" fue la última fecha del calendario compuesta únicamente por dígitos impares que ocurriría durante mucho tiempo, y "2000/02/02" fue la primera fecha compuesta únicamente por dígitos pares que ocurrió en mucho tiempo. [63] Dado que estos resultados utilizan el 0 como par, algunos lectores no estuvieron de acuerdo con la idea. [64]
En las pruebas estandarizadas , si una pregunta indaga sobre el comportamiento de los números pares, puede ser necesario tener en cuenta que el cero es par. [65] Las publicaciones oficiales relacionadas con los exámenes GMAT y GRE establecen que el 0 es par. [66]
La paridad del cero es relevante para el racionamiento de días pares e impares , en el que los automóviles pueden circular o comprar gasolina en días alternos, según la paridad del último dígito de sus matrículas . La mitad de los números en un rango dado terminan en 0, 2, 4, 6, 8 y la otra mitad en 1, 3, 5, 7, 9, por lo que tiene sentido incluir el 0 con los otros números pares. Sin embargo, en 1977, un sistema de racionamiento en París provocó confusión: en un día solo impar, la policía evitó multar a los conductores cuyas matrículas terminaran en 0, porque no sabían si el 0 era par. [67] Para evitar tal confusión, la legislación pertinente a veces estipula que el cero es par; tales leyes se han aprobado en Nueva Gales del Sur [68] y Maryland . [69]
En los buques de la Armada de los Estados Unidos, los compartimentos con números pares se encuentran en el costado de babor , pero el cero se reserva para los compartimentos que intersecan la línea central. Es decir, los números se leen 6-4-2-0-1-3-5 de babor a estribor. [70]
En el juego de la ruleta , el número 0 no cuenta como par o impar, lo que le da al casino una ventaja en tales apuestas. [71] De manera similar, la paridad del cero puede afectar los pagos en apuestas paralelas cuando el resultado depende de si un número aleatorio es par o impar, y resulta ser cero. [72]
El juego de “ pares e impares ” también se ve afectado: si ambos jugadores no tienen dedos en la mano, el número total de dedos es cero, por lo que el jugador par gana. [73] Un manual para profesores sugiere jugar a este juego como una forma de introducir a los niños al concepto de que 0 es divisible por 2. [74]
Referencias
- ^ ab Arnold 1919, pág. 21 "Mediante la misma prueba, el cero supera a todos los números en 'paridad'". Wong 1997, pág. 479 "Por lo tanto, el entero b 000⋯000 = 0 es el más 'par'".
- ^ Penner 1999, p. 34: Lema B.2.2, El entero 0 es par y no es impar . Penner utiliza el símbolo matemático ∃, el cuantificador existencial , para enunciar la prueba: "Para ver que 0 es par, debemos demostrar que ∃ k (0 = 2 k ), y esto se sigue de la igualdad 0 = 2 ⋅ 0 ."
- ^ Ball, Lewis y Thames (2008, p. 15) analizan este desafío para el docente de primaria, que quiere dar razones matemáticas para hechos matemáticos, pero cuyos estudiantes no usan la misma definición ni la entenderían si se les presentara.
- ^ Compárese con Lichtenberg (1972, p. 535) Fig. 1
- ^ Lichtenberg 1972, pp. 535–536 "...los números responden a la pregunta ¿cuántos? para el conjunto de objetos... cero es la propiedad numérica del conjunto vacío... Si los elementos de cada conjunto están marcados en grupos de dos... entonces el número de ese conjunto es un número par".
- ^ Lichtenberg 1972, pp. 535–536 "Se han rodeado grupos de dos estrellas en cero. No quedan estrellas. Por lo tanto, cero es un número par".
- ^ Dickerson y Pitman 2012, pág. 191.
- ^ Lichtenberg 1972, p. 537; compárese con su figura 3. "Si los números pares se identifican de alguna manera especial... no hay razón alguna para omitir el cero del patrón".
- ^ Lichtenberg 1972, pp. 537–538 "En un nivel más avanzado... los números expresados como (2 × ▢) + 0 son números pares... el cero encaja muy bien en este patrón".
- ^ Caldwell y Xiong 2012, págs. 5-6.
- ^ Gowers 2002, p. 118 "La exclusión aparentemente arbitraria del 1 de la definición de primo... no expresa ningún hecho profundo sobre los números: resulta ser simplemente una convención útil, adoptada para que haya una sola manera de factorizar cualquier número dado en primos". Para una discusión más detallada, véase Caldwell y Xiong (2012).
- ^ abc Partee 1978, pág. xxi
- ^ ab Stewart 2001, pág. 54 Se dan estas reglas, pero no se citan textualmente.
- ^ Devlin 1985, págs. 30-33
- ^ Penner 1999, pág. 34.
- ^ ab Berlinghoff, Grant y Skrien 2001 Para vértices aislados, consulte la pág. 149; para grupos, consulte la pág. 311.
- ^ Lovász, Pelikán y Vesztergombi 2003, págs. 127-128
- ^ Starr 1997, págs. 58-62
- ^ Frontera 1985, págs. 23-25
- ^ Lorentz 1994, págs. 5-6; Lovás y Pfenning 2008, pág. 115; Nipkow, Paulson y Wenzel 2002, pág. 127
- ^ Bunch 1982, pág. 165
- ^ Salzmann y col. 2007, pág. 168
- ^ Wise 2002, págs. 66-67
- ^ Anderson 2001, pag. 53; Hartsfield y Ringel 2003, pág. 28
- ^ Dummit y Foote 1999, pág. 48
- ^ Andrews 1990, pág. 100
- ^ Tabachnikova y Smith 2000, pag. 99; Anderson y Feil 2005, págs. 437–438
- ^ Barbeau 2003, pág. 98
- ^ Wong 1997, pág. 479
- ^ Gouvêa 1997, p. 25 De un primo general p : "El razonamiento aquí es que ciertamente podemos dividir 0 por p , y la respuesta es 0, que podemos dividir por p , y la respuesta es 0, que podemos dividir por p ..." (puntos suspensivos en el original)
- ^ Krantz 2001, pág. 4
- ^ Salzmann y col. 2007, pág. 224
- ^ de Frobisher 1999, pág. 41
- ^ Este es el período en Estados Unidos, Canadá, Gran Bretaña, Australia e Israel; véase Levenson, Tsamir y Tirosh (2007, pág. 85).
- ^ Frobisher 1999, págs. 31 (Introducción), 40-41 (El número cero), 48 (Implicaciones para la enseñanza)
- ^ Frobisher 1999, pp. 37, 40, 42; los resultados proceden de la encuesta realizada a mediados del verano de 1992.
- ^ Frobisher 1999, p. 41 "El porcentaje de niños de segundo año que deciden que cero es un número par es mucho menor que en el estudio anterior, 32 por ciento en comparación con el 45 por ciento"
- ^ Frobisher 1999, p. 41 "El éxito en decidir que el cero es un número par no siguió aumentando con la edad, ya que aproximadamente uno de cada dos niños en cada uno de los años 2 a 6 ponía una marca en la casilla de 'pares'..."
- ^ Frobisher 1999, págs. 40–42, 47; estos resultados provienen del estudio de febrero de 1999, que incluyó a 481 niños de tres escuelas con distintos niveles de rendimiento.
- ^ Frobisher 1999, pág. 41, atribuido a "Jonathan"
- ^ Frobisher 1999, pág. 41, atribuido a "José"
- ^ Frobisher 1999, pág. 41, atribuido a "Richard"
- ^ Keith 2006, pp. 35–68 "Hubo poco desacuerdo sobre la idea de que el cero es un número par. Los estudiantes convencieron a los pocos que no estaban seguros con dos argumentos. El primer argumento fue que los números siguen un patrón... impar, par, impar, par, impar, par... y como dos es par y uno es impar, entonces el número anterior al uno, que no es una fracción, sería cero. Por lo tanto, el cero tendría que ser par. El segundo argumento fue que si una persona tiene cero cosas y las coloca en dos grupos iguales, entonces habrá cero en cada grupo. Los dos grupos tendrán la misma cantidad, cero".
- ^ Levenson, Tsamir y Tirosh 2007, págs. 83–95
- ^ ab Ball, Lewis & Thames 2008, p. 27, Figura 1.5 "Afirmaciones matemáticas sobre el cero".
- ^ Ball, Lewis y Thames 2008, pág. 16.
- ^ Levenson, Tsamir y Tirosh 2007; Dickerson y Pitman 2012
- ^ Dickerson y Pitman 2012.
- ^ Ball, Hill y Bass 2005, págs. 14-16
- ^ Hill et al. 2008, págs. 446–447.
- ^ Lichtenberg 1972, pág. 535
- ^ Ball, Lewis & Thames 2008, pág. 15. Véase también la nota clave de Ball para un análisis más detallado de las definiciones apropiadas.
- ^ Como concluyen Levenson, Tsamir y Tirosh (2007, pág. 93), haciendo referencia a Freudenthal (1983, pág. 460)
- ^ Nuerk, Iversen y Willmes (2004, p. 851): "También se puede observar que el cero difiere fuertemente de todos los demás números independientemente de si se responde con la mano izquierda o derecha. (Véase la línea que separa el cero de los demás números.)"
- ^ Véanse los datos de Dehaene, Bossini y Giraux (1993) y el resumen de Nuerk, Iversen y Willmes (2004, p. 837).
- ^ Dehaene, Bossini y Giraux 1993, págs. 374–376
- ^ Dehaene, Bossini y Giraux 1993, págs. 376–377
- ^ Dehaene, Bossini y Giraux 1993, p. 376 "En cierto sentido intuitivo, la noción de paridad es familiar sólo para números mayores que 2. De hecho, antes del experimento, algunos sujetos L no estaban seguros de si 0 era par o impar y tuvieron que recordarles la definición matemática. La evidencia, en resumen, sugiere que en lugar de calcularse sobre la marcha utilizando un criterio de divisibilidad por 2, la información de paridad se recupera de la memoria junto con una serie de otras propiedades semánticas... Si se accede a una memoria semántica en los juicios de paridad, entonces se deberían encontrar diferencias interindividuales dependiendo de la familiaridad de los sujetos con los conceptos numéricos".
- ^ Nuerk, Iversen y Willmes 2004, págs. 838, 860–861
- ^ Grimes 1975, p. 156 "...uno puede plantear las siguientes preguntas a parejas casadas que conoce: (1) ¿Es el cero un número par? ... Muchas parejas no están de acuerdo..."
- ^ Wilden y Hammer 1987, pág. 104
- ^ Nieve 2001; Morgan 2001
- ^ Steinberg 1999; Siegel 1999; Stingl 2006
- ^ Sones & Sones 2002 "De ello se deduce que el cero es par, y que el 20/2/2000 resuelve el problema de forma muy acertada. Sin embargo, siempre sorprende la cantidad de gente que se molesta por llamar par al cero..."; Lectores de la Columna 8 2006a "'...según los matemáticos, el número cero, junto con los números negativos y las fracciones, no es ni par ni impar', escribe Etan..."; Lectores de la Columna 8 2006b "'Estoy de acuerdo en que el cero es par, pero ¿es prudente que el profesor Bunder lo 'demuestre' afirmando que 0 = 2 x 0? Según esa lógica (de un doctorado en lógica matemática, nada menos), como 0 = 1 x 0, ¡también es impar!' El profesor lo discutirá y, lógicamente, tiene una base sólida para hacerlo, pero puede que estemos usando un poco este tema..."
- ^ Personal de Kaplan 2004, pág. 227
- ^ Consejo de Admisión de Posgrado en Gestión 2005, págs. 108, 295–297; Servicio de Evaluación Educativa 2009, pág. 1
- ^ Arsham 2002; La cita se atribuye a la emisión actual del 1 de octubre de 1977. El relato de Arsham es repetido por Crumpacker (2007, p. 165).
- ^ Sones & Sones 2002 "El matemático de la Universidad Estatal de Pensilvania George Andrews, que recuerda una época de racionamiento de gasolina en Australia... Entonces alguien en el parlamento de Nueva Gales del Sur afirmó que esto significaba que las placas que terminaban en cero nunca podrían recibir gasolina, porque 'el cero no es ni par ni impar. Así que el parlamento de Nueva Gales del Sur dictaminó que, a los efectos del racionamiento de gasolina, ¡el cero es un número par!'"
- ^ Una ley de Maryland de 1980 especifica: "(a) En las fechas pares del calendario, la gasolina solo podrá ser comprada por operadores de vehículos que tengan placas de matrícula personalizadas que no contengan números y placas de matrícula cuyo último dígito termine en un número par. Esto no incluirá las placas de radioaficionados. El cero es un número par; (b) En las fechas impares del calendario..." Cita parcial tomada de Department of Legislative Reference (1974), Laws of the State of Maryland, Volume 2, p. 3236 , consultado el 2 de junio de 2013
- ^ Cutler 2008, págs. 237-238
- ^ Brisman 2004, pág. 153
- ^ Smock 2006; Hohmann 2007; Turner 1996
- ^ Diagram Group 1983, pág. 213
- ^ Baroody y Coslick 1998, pág. 1.33
Bibliografía
- Anderson, Ian (2001), Un primer curso de matemáticas discretas , Londres, Reino Unido: Springer, ISBN 978-1-85233-236-5
- Anderson, Marlow; Feil, Todd (2005), Un primer curso de álgebra abstracta: anillos, grupos y campos , Londres, Reino Unido: CRC Press, ISBN 978-1-58488-515-3
- Andrews, Edna (1990), Teoría de la marcación: la unión de la asimetría y la semiosis en el lenguaje , Durham: Duke University Press, ISBN 978-0-8223-0959-8
- Arnold, CL (enero de 1919), "El número cero", The Ohio Educational Monthly , 68 (1): 21–22 , consultado el 11 de abril de 2010
- Arsham, Hossein (enero de 2002), "Zero in Four Dimensions: Historical, Psychological, Cultural, and Logical Perspectives", The Pantaneto Forum , archivado desde el original el 25 de septiembre de 2007 , consultado el 24 de septiembre de 2007
- Ball, Deborah Loewenberg; Hill, Heather C.; Bass, Hyman (2005), "Conocer las matemáticas para enseñar: ¿quién sabe matemáticas lo suficientemente bien como para enseñar en tercer grado y cómo podemos decidirlo?", American Educator , hdl :2027.42/65072
- Ball, Deborah Loewenberg; Lewis, Jennifer; Thames, Mark Hoover (2008), "Cómo hacer que las matemáticas funcionen en la escuela" (PDF) , Journal for Research in Mathematics Education , M14 : 13–44 y 195–200 , consultado el 4 de marzo de 2010
- Barbeau, Edward Joseph (2003), Polinomios , Springer, ISBN 978-0-387-40627-5
- Baroody, Arthur; Coslick, Ronald (1998), Fomentar el poder matemático de los niños: un enfoque investigativo para K-8 , Lawrence Erlbaum Associates, ISBN 978-0-8058-3105-4
- Berlinghoff, William P.; Grant, Kerry E.; Skrien, Dale (2001), Una muestra de matemáticas: temas para las artes liberales (quinta edición revisada), Rowman & Littlefield, ISBN 978-0-7425-0202-4
- Border, Kim C. (1985), Teoremas de punto fijo con aplicaciones a la economía y la teoría de juegos , Cambridge University Press, ISBN 978-0-521-38808-5
- Brisman, Andrew (2004), Guía de Mensa para jugar en casinos: formas de ganar , Sterling, ISBN 978-1-4027-1300-2
- Bunch, Bryan H. (1982), Falacias y paradojas matemáticas , Van Nostrand Reinhold, ISBN 978-0-442-24905-2
- Caldwell, Chris K.; Xiong, Yeng (2012-12-27), "¿Cuál es el primo más pequeño?", Journal of Integer Sequences , 15 (9), arXiv : 1209.2007 , Bibcode :2012arXiv1209.2007C
- Lectores de la columna 8 (10-03-2006), "Columna 8", The Sydney Morning Herald (Primera edición), pág. 18, Factiva SMHH000020060309e23a00049
{{citation}}: CS1 maint: nombres numéricos: lista de autores ( enlace ) - Lectores de la columna 8 (16 de marzo de 2006), "Columna 8", The Sydney Morning Herald (primera edición), pág. 20, Factiva SMHH000020060315e23g0004z
{{citation}}: CS1 maint: nombres numéricos: lista de autores ( enlace ) - Crumpacker, Bunny (2007), Figuras perfectas: la tradición de los números y cómo aprendimos a contar, Macmillan, ISBN 978-0-312-36005-4
- Cutler, Thomas J. (2008), Manual del marinero: Armada de los Estados Unidos (edición centenaria), Naval Institute Press, ISBN 978-1-55750-221-6
- Dehaene, Stanislas ; Bossini, Serge; Giraux, Pascal (1993), "La representación mental de la paridad y la magnitud numérica" (PDF) , Journal of Experimental Psychology: General , 122 (3): 371–396, doi :10.1037/0096-3445.122.3.371, archivado desde el original (PDF) el 2011-07-19 , consultado el 2007-09-13
- Devlin, Keith (abril de 1985), "La edad de oro de las matemáticas", New Scientist , 106 (1452)
- Diagram Group (1983), La enciclopedia oficial mundial de deportes y juegos, Paddington Press, ISBN 978-0-448-22202-8
- Dickerson, David S.; Pitman, Damien J. (julio de 2012), Tai-Yih Tso (ed.), "Categorización y uso de definiciones matemáticas por parte de estudiantes universitarios avanzados" (PDF) , Actas de la 36.ª Conferencia del Grupo Internacional de Psicología de la Educación Matemática , 2 : 187–195
- Dummit, David S.; Foote, Richard M. (1999), Álgebra abstracta (2.ª ed.), Nueva York, EE. UU.: Wiley, ISBN 978-0-471-36857-1
- Educational Testing Service (2009), Convenciones matemáticas para la medida de razonamiento cuantitativo del examen general revisado del GRE (PDF) , Educational Testing Service , consultado el 6 de septiembre de 2011
- Freudenthal, Hans (1983), Fenomenología didáctica de las estructuras matemáticas , Dordrecht, Países Bajos: Reidel
- Frobisher, Len (1999), "El conocimiento de los números pares e impares por parte de los niños de la escuela primaria", en Anthony Orton (ed.), Pattern in the Teaching and Learning of Mathematics , Londres, Reino Unido: Cassell, págs. 31-48
- Gouvea, Fernando Quadros (1997),Números p -ádicos: una introducción (2.ª ed.), Springer-Verlag, ISBN 978-3-540-62911-5
- Gowers, Timothy (2002), Matemáticas: una introducción muy breve , Oxford University Press , ISBN 978-0-19-285361-5
- Graduate Management Admission Council (septiembre de 2005), The Official Guide for GMAT Review (11.ª ed.), McLean, Virginia, EE. UU.: Graduate Management Admission Council, ISBN 978-0-9765709-0-5
- Grimes, Joseph E. (1975), El hilo del discurso , Walter de Gruyter, ISBN 978-90-279-3164-1
- Hartsfield, Nora; Ringel, Gerhard (2003), Perlas en la teoría de grafos: una introducción completa , Mineola, Nueva York, EE. UU.: Courier Dover, ISBN 978-0-486-43232-8
- Hill, Heather C.; Blunk, Merrie L.; Charalambous, Charalambos Y.; Lewis, Jennifer M.; Phelps, Geoffrey C.; Sleep, Laurie; Ball, Deborah Loewenberg (2008), "Conocimiento matemático para la enseñanza y la calidad matemática de la instrucción: un estudio exploratorio", Cognition and Instruction , 26 (4): 430–511, doi : 10.1080/07370000802177235
- Hohmann, George (2007-10-25), "Las empresas dejan que el mercado determine el nuevo nombre", Charleston Daily Mail , p. P1C, Factiva CGAZ000020071027e3ap0001l
- Personal de Kaplan (2004), Kaplan SAT 2400, edición de 2005, Simon and Schuster, ISBN 978-0-7432-6035-0
- Keith, Annie (2006), "Argumento matemático en una clase de segundo grado: generación y justificación de afirmaciones generalizadas sobre números pares e impares", Teachers Engaged in Research: Inquiry in Mathematics Classrooms, Grados Pre-K-2 , IAP, ISBN 978-1-59311-495-4
- Krantz, Steven George (2001), Diccionario de álgebra, aritmética y trigonometría, CRC Press, ISBN 978-1-58488-052-3
- Levenson, Esther; Tsamir, Pessia; Tirosh, Dina (2007), "Ni par ni impar: dilemas de los estudiantes de sexto grado con respecto a la paridad del cero", The Journal of Mathematical Behavior , 26 (2): 83–95, doi :10.1016/j.jmathb.2007.05.004
- Lichtenberg, Betty Plunkett (noviembre de 1972), "El cero es un número par", The Arithmetic Teacher , 19 (7): 535–538, doi :10.5951/AT.19.7.0535
- Lorentz, Richard J. (1994), Algoritmos recursivos , Intellect Books, ISBN 978-1-56750-037-0
- Lovas, William; Pfenning, Frank (22 de enero de 2008), "Un sistema de refinamiento de tipos bidireccional para LF", Electronic Notes in Theoretical Computer Science , 196 : 113–128, doi : 10.1016/j.entcs.2007.09.021
- Lovász, László ; Pelikán, József; Vesztergombi, Katalin L. (2003), Matemáticas discretas: elemental y más allá , Springer, ISBN 978-0-387-95585-8
- Morgan, Frank (5 de abril de 2001), "Old Coins", Frank Morgan's Math Chat , The Mathematical Association of America, archivado desde el original el 8 de enero de 2009 , consultado el 22 de agosto de 2009
- Nipkow, Tobias ; Paulson, Lawrence C. ; Wenzel, Markus (2002), Isabelle/Hol: Un asistente de prueba para lógica de orden superior , Springer, ISBN 978-3-540-43376-7
- Nuerk, Hans-Christoph; Iversen, Wiebke; Willmes, Klaus (julio de 2004), "Modulación notacional del efecto SNARC y MARC (marcación lingüística de los códigos de respuesta)", The Quarterly Journal of Experimental Psychology A , 57 (5): 835–863, doi :10.1080/02724980343000512, PMID 15204120, S2CID 10672272
- Partee, Barbara Hall (1978), Fundamentos de matemáticas para la lingüística , Dordrecht, Países Bajos: D. Reidel, ISBN 978-90-277-0809-0
- Penner, Robert C. (1999), Matemáticas discretas: técnicas de prueba y estructuras matemáticas , River Edge: World Scientific, ISBN 978-981-02-4088-2
- Salzmann, Helmut; Grundhofer, Theo; Hähl, Hermann; Löwen, Rainer (2007), Los campos clásicos: características estructurales de los números reales y racionales , Cambridge University Press, ISBN 978-0-521-86516-6
- Siegel, Robert (1999-11-19), "Análisis: La fecha de hoy se indica con abreviaturas que utilizan sólo números impares. 1-1, 1-9, 1-9-9-9. La próxima vez que eso ocurra será dentro de más de mil años.", All Things Considered , National Public Radio
- Smock, Doug (6 de febrero de 2006), "Las apuestas impares: Hines Ward contra Tiger Woods", Charleston Gazette , pág. P1B, Factiva CGAZ000020060207e226000bh
- Snow, Tony (23 de febrero de 2001), "Los tontos de Bubba", Jewish World Review , consultado el 22 de agosto de 2009
- Sones, Bill; Sones, Rich (8 de mayo de 2002), "Para ocultar tu edad, cierra los labios", Deseret News , pág. C07, archivado desde el original el 8 de mayo de 2015 , consultado el 21 de junio de 2014
- Starr, Ross M. (1997), Teoría del equilibrio general: una introducción , Cambridge University Press, ISBN 978-0-521-56473-1
- Steinberg, Neil (30 de noviembre de 1999), "Años pares, hechos impares", Chicago Sun-Times (quinta edición), pág. 50, Factiva chi0000020010826dvbu0119h
- Stewart, Mark Alan (2001), 30 días para el examen GMAT CAT , Stamford: Thomson, ISBN 978-0-7689-0635-6
- Stingl, Jim (2006-04-05), "01:02:03 04/05/06; Podemos contar con algunas cosas en la vida", Milwaukee Journal Sentinel (Final ed.), p. B1, archivado desde el original el 2006-04-27 , consultado el 2014-06-21
- Tabachnikova, Olga M.; Smith, Geoff C. (2000), Temas de teoría de grupos , Londres, Reino Unido: Springer, ISBN 978-1-85233-235-8
- Los participantes del Foro de Matemáticas (2000), "Una pregunta en torno al cero", Foro de Matemáticas » Discusiones » Historia » Historia-Matematica , Drexel University , consultado el 25 de septiembre de 2007
- Turner, Julian (13 de julio de 1996), "Apuestas deportivas: para Lytham, mire hacia el Pacífico Sur", The Guardian , pág. 23, Factiva grdn000020011017ds7d00bzg
- Wilden, Anthony; Hammer, Rhonda (1987), Las reglas no son un juego: la estrategia de la comunicación , Routledge Kegan & Paul, ISBN 978-0-7100-9868-9
- Wise, Stephen (2002), Fundamentos de SIG , CRC Press, ISBN 978-0-415-24651-4
- Wong, Samuel Shaw Ming (1997), Métodos computacionales en física e ingeniería , World Scientific, ISBN 978-981-02-3043-2
Lectura adicional
- Matousek, John (2001-03-28), "Cero impar/par: ¿es cero par?", Ask Dr. Math , The Math Forum, archivado del original el 2020-11-29 , consultado el 2013-06-06
- Adams, Cecil (1999), "¿El cero es par o impar?", The Straight Dope , archivado desde el original el 2022-07-14 , consultado el 2013-06-06
Enlaces externos
 Medios relacionados con Paridad de cero en Wikimedia Commons
Medios relacionados con Paridad de cero en Wikimedia Commons- ¿El cero es par? - Numberphile, vídeo con James Grime, Universidad de Nottingham


