Árbol de decisión

Un árbol de decisiones es una estructura de partición recursiva de apoyo a la toma de decisiones que utiliza un modelo de árbol de decisiones y sus posibles consecuencias, incluidos los resultados de eventos aleatorios , los costos de los recursos y la utilidad . Es una forma de mostrar un algoritmo que solo contiene declaraciones de control condicional.
Los árboles de decisión se utilizan comúnmente en la investigación de operaciones , específicamente en el análisis de decisiones , [1] para ayudar a identificar una estrategia con más probabilidades de alcanzar un objetivo, pero también son una herramienta popular en el aprendizaje automático .
Descripción general
Un árbol de decisiones es una estructura similar a un diagrama de flujo en el que cada nodo interno representa una "prueba" sobre un atributo (por ejemplo, si al lanzar una moneda sale cara o cruz), cada rama representa el resultado de la prueba y cada nodo de hoja representa una etiqueta de clase (decisión tomada después de calcular todos los atributos). Las rutas desde la raíz hasta la hoja representan reglas de clasificación .
En el análisis de decisiones , se utiliza un árbol de decisiones y el diagrama de influencia estrechamente relacionado como una herramienta de apoyo visual y analítica a la toma de decisiones, donde se calculan los valores esperados (o utilidad esperada ) de las alternativas en competencia.
Un árbol de decisión consta de tres tipos de nodos: [2]
- Nodos de decisión: normalmente representados por cuadrados
- Nodos de azar: normalmente representados por círculos
- Nodos finales: normalmente representados por triángulos
Los árboles de decisión se utilizan habitualmente en la investigación de operaciones y la gestión de operaciones . Si, en la práctica, las decisiones deben tomarse en línea sin recordar nada y con un conocimiento incompleto, un árbol de decisión debería ir acompañado de un modelo de probabilidad como modelo de mejor elección o algoritmo de modelo de selección en línea . [ cita requerida ] Otro uso de los árboles de decisión es como medio descriptivo para calcular probabilidades condicionales .
Los árboles de decisión, los diagramas de influencia , las funciones de utilidad y otras herramientas y métodos de análisis de decisiones se enseñan a los estudiantes universitarios en las escuelas de negocios, economía de la salud y salud pública, y son ejemplos de métodos de investigación de operaciones o de ciencia de la gestión . Estas herramientas también se utilizan para predecir las decisiones de los hogares en situaciones normales y de emergencia. [3] [4]
Bloques de construcción del árbol de decisiones
Elementos del árbol de decisiones
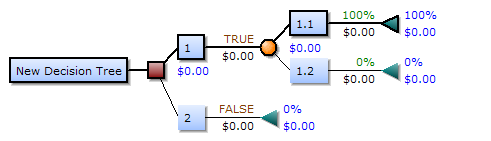
Dibujado de izquierda a derecha, un árbol de decisión solo tiene nodos de ruptura (caminos de división) pero no nodos de hundimiento (caminos de convergencia). Por lo tanto, si se utilizan manualmente, pueden llegar a ser muy grandes y, a menudo, es difícil dibujarlos completamente a mano. Tradicionalmente, los árboles de decisión se han creado manualmente (como muestra el ejemplo que se muestra al margen), aunque cada vez se utiliza más software especializado.
Reglas de decisión
El árbol de decisión se puede linealizar en reglas de decisión [ 5] , donde el resultado es el contenido del nodo hoja y las condiciones a lo largo de la ruta forman una conjunción en la cláusula if. En general, las reglas tienen la forma:
- Si condición1 y condición2 y condición3 entonces resultado.
Las reglas de decisión se pueden generar construyendo reglas de asociación con la variable objetivo a la derecha. También pueden denotar relaciones temporales o causales. [6]
Árbol de decisiones utilizando símbolos de diagrama de flujo
Por lo general, los árboles de decisiones se dibujan utilizando símbolos de diagramas de flujo , ya que son más fáciles de leer y comprender para muchos. Tenga en cuenta que hay un error conceptual en el cálculo de "Proceder" del árbol que se muestra a continuación; el error se relaciona con el cálculo de los "costos" adjudicados en una acción legal.
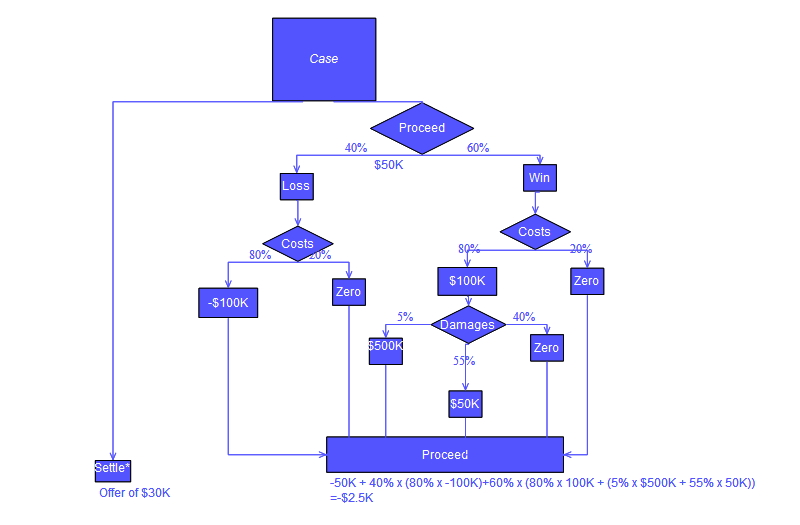
Ejemplo de análisis
El análisis puede tener en cuenta la preferencia o la función de utilidad del tomador de decisiones (por ejemplo, la empresa) , por ejemplo:
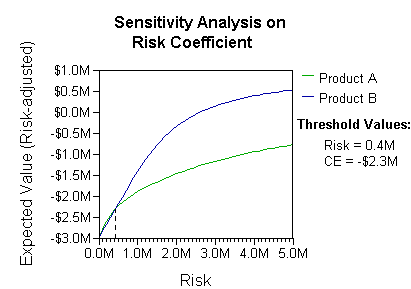
La interpretación básica en esta situación es que la empresa prefiere el riesgo y los beneficios de B bajo coeficientes de preferencia de riesgo realistas (superiores a 400.000 dólares; en ese rango de aversión al riesgo, la empresa necesitaría modelar una tercera estrategia, "Ni A ni B").
Otro ejemplo, que se utiliza con frecuencia en los cursos de investigación de operaciones , es la distribución de los salvavidas en las playas (también conocido como el ejemplo "La vida es una playa"). [7] El ejemplo describe dos playas con salvavidas que se distribuirán en cada una de ellas. Existe un presupuesto máximo B que se puede distribuir entre las dos playas (en total) y, utilizando una tabla de rendimientos marginales, los analistas pueden decidir cuántos salvavidas asignar a cada playa.
| Socorristas en cada playa | Se evitaron ahogamientos en total, playa #1 | Se evitaron ahogamientos en total, playa #2 |
|---|---|---|
| 1 | 3 | 1 |
| 2 | 0 | 4 |
En este ejemplo, se puede dibujar un árbol de decisiones para ilustrar los principios de rendimientos decrecientes en la playa n.° 1.
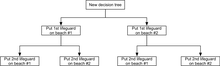
El árbol de decisiones ilustra que, al distribuir a los socorristas de manera secuencial, lo óptimo sería colocar al primer socorrista en la playa n.° 1 si solo se cuenta con presupuesto para un socorrista. Pero si se cuenta con presupuesto para dos socorristas, colocar a ambos en la playa n.° 2 evitaría más ahogamientos en general.

Diagrama de influencia
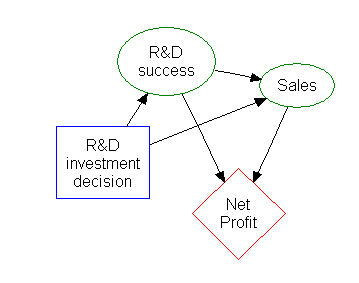
Gran parte de la información de un árbol de decisiones se puede representar de forma más compacta como un diagrama de influencia , centrando la atención en los problemas y las relaciones entre los eventos.
Inducción de las reglas de la asociación
Los árboles de decisión también pueden considerarse modelos generativos de reglas de inducción a partir de datos empíricos. Un árbol de decisión óptimo se define entonces como un árbol que tiene en cuenta la mayor parte de los datos, al tiempo que minimiza el número de niveles (o "preguntas"). [8] Se han ideado varios algoritmos para generar dichos árboles óptimos, como ID3 /4/5, [9] CLS, ASSISTANT y CART.
Ventajas y desventajas
Entre las herramientas de apoyo a la toma de decisiones, los árboles de decisión (y los diagramas de influencia ) tienen varias ventajas. Los árboles de decisión:
- Son fáciles de entender e interpretar. Las personas pueden comprender los modelos de árboles de decisión después de una breve explicación.
- Tener valor incluso con pocos datos concretos. Se pueden generar conocimientos importantes a partir de la descripción que hacen los expertos de una situación (sus alternativas, probabilidades y costos) y sus preferencias en cuanto a los resultados.
- Ayuda a determinar los peores, mejores y esperados valores para diferentes escenarios.
- Utilice un modelo de caja blanca . Si un resultado determinado lo proporciona un modelo.
- Se puede combinar con otras técnicas de decisión.
- Se puede considerar la acción de más de un tomador de decisiones.
Desventajas de los árboles de decisión:
- Son inestables, lo que significa que un pequeño cambio en los datos puede conducir a un gran cambio en la estructura del árbol de decisión óptimo.
- Suelen ser relativamente imprecisos. Muchos otros predictores funcionan mejor con datos similares. Esto se puede solucionar reemplazando un único árbol de decisión por un bosque aleatorio de árboles de decisión, pero un bosque aleatorio no es tan fácil de interpretar como un único árbol de decisión.
- En el caso de datos que incluyen variables categóricas con diferentes números de niveles, la ganancia de información en los árboles de decisión está sesgada a favor de aquellos atributos con más niveles. [10]
- Los cálculos pueden volverse muy complejos, especialmente si muchos valores son inciertos y/o si muchos resultados están vinculados.
Optimización de un árbol de decisiones
Hay algunas cosas que se deben tener en cuenta al mejorar la precisión del clasificador de árboles de decisión. A continuación, se presentan algunas posibles optimizaciones que se deben tener en cuenta para asegurarse de que el modelo de árbol de decisión producido tome la decisión o la clasificación correctas. Tenga en cuenta que estas no son las únicas cosas que se deben tener en cuenta, sino solo algunas.
Aumentar el número de niveles del árbol
La precisión del árbol de decisión puede cambiar en función de la profundidad del árbol de decisión. En muchos casos, las hojas del árbol son nodos puros . [11] Cuando un nodo es puro, significa que todos los datos en ese nodo pertenecen a una sola clase. [12] Por ejemplo, si las clases en el conjunto de datos son Cáncer y No Cáncer, un nodo hoja se consideraría puro cuando todos los datos de muestra en un nodo hoja son parte de una sola clase, ya sea cáncer o no cáncer. Es importante tener en cuenta que un árbol más profundo no siempre es mejor cuando se optimiza el árbol de decisión. Un árbol más profundo puede influir en el tiempo de ejecución de forma negativa. Si se utiliza un determinado algoritmo de clasificación, un árbol más profundo podría significar que el tiempo de ejecución de este algoritmo de clasificación sea significativamente más lento. También existe la posibilidad de que el algoritmo real que construye el árbol de decisión se vuelva significativamente más lento a medida que el árbol se hace más profundo. Si el algoritmo de construcción del árbol que se utiliza divide los nodos puros, se podría experimentar una disminución en la precisión general del clasificador del árbol. Ocasionalmente, profundizar más en el árbol puede provocar una disminución de la precisión en general, por lo que es muy importante probar modificando la profundidad del árbol de decisión y seleccionar la profundidad que produzca mejores resultados. Para resumir, observe los puntos a continuación, definiremos el número D como la profundidad del árbol.
Posibles ventajas de aumentar el número D:
- La precisión del modelo de clasificación del árbol de decisiones aumenta.
Posibles desventajas de aumentar D
- Problemas de ejecución
- Disminución de la precisión en general
- Las divisiones de nodos puros al profundizar pueden causar problemas.
Es imprescindible poder comprobar las diferencias en los resultados de la clasificación al cambiar el valor D. Debemos poder cambiar y comprobar fácilmente las variables que podrían afectar la precisión y la fiabilidad del modelo de árbol de decisiones.
La elección de funciones de división de nodos
La función de división de nodos utilizada puede tener un impacto en la mejora de la precisión del árbol de decisión. Por ejemplo, el uso de la función de ganancia de información puede producir mejores resultados que el uso de la función phi. La función phi se conoce como una medida de la “bondad” de una división candidata en un nodo del árbol de decisión. La función de ganancia de información se conoce como una medida de la “reducción de la entropía ”. A continuación, crearemos dos árboles de decisión. Un árbol de decisión se creará utilizando la función phi para dividir los nodos y un árbol de decisión se creará utilizando la función de ganancia de información para dividir los nodos.
Principales ventajas y desventajas de la ganancia de información y la función phi
- Una desventaja importante de la ganancia de información es que la característica que se elige como el siguiente nodo en el árbol tiende a tener valores más únicos. [13]
- Una ventaja de la obtención de información es que tiende a elegir las características más impactantes que están cerca de la raíz del árbol. Es una muy buena medida para decidir la relevancia de algunas características.
- La función phi también es una buena medida para decidir la relevancia de algunas características en función de su "bondad".
Esta es la fórmula de la función de ganancia de información. La fórmula establece que la ganancia de información es una función de la entropía de un nodo del árbol de decisión menos la entropía de una división candidata en el nodo t de un árbol de decisión.
Esta es la fórmula de la función phi. La función phi se maximiza cuando la característica elegida divide las muestras de manera que produzca divisiones homogéneas y tenga aproximadamente la misma cantidad de muestras en cada división.
Fijaremos D, que es la profundidad del árbol de decisión que estamos construyendo, en tres (D = 3). También tenemos el siguiente conjunto de datos de muestras de cáncer y de otras enfermedades y las características de mutación que tienen o no tienen las muestras. Si una muestra tiene una mutación característica, entonces la muestra es positiva para esa mutación y estará representada por uno. Si una muestra no tiene una mutación característica, entonces la muestra es negativa para esa mutación y estará representada por cero.
En resumen, C significa cáncer y NC significa no cáncer. La letra M significa mutación y, si una muestra tiene una mutación particular, aparecerá en la tabla como un uno y, de lo contrario, como un cero.
| M1 | M2 | M3 | M4 | M5 | |
|---|---|---|---|---|---|
| C1 | 0 | 1 | 0 | 1 | 1 |
| NC1 | 0 | 0 | 0 | 0 | 0 |
| NC2 | 0 | 0 | 1 | 1 | 0 |
| NC3 | 0 | 0 | 0 | 0 | 0 |
| C2 | 1 | 1 | 1 | 1 | 1 |
| NC4 | 0 | 0 | 0 | 1 | 0 |
Ahora, podemos usar las fórmulas para calcular los valores de la función phi y los valores de ganancia de información para cada M en el conjunto de datos. Una vez que se calculan todos los valores, se puede generar el árbol. Lo primero que se debe hacer es seleccionar el nodo raíz. En la ganancia de información y la función phi, consideramos que la división óptima es la mutación que produce el valor más alto para la ganancia de información o la función phi. Ahora supongamos que M1 tiene el valor más alto de la función phi y M4 tiene el valor más alto de ganancia de información. La mutación M1 será la raíz de nuestro árbol de función phi y M4 será la raíz de nuestro árbol de ganancia de información. Puede observar los nodos raíz a continuación.

Ahora, una vez que hemos elegido el nodo raíz, podemos dividir las muestras en dos grupos en función de si una muestra es positiva o negativa para la mutación del nodo raíz. Los grupos se denominarán grupo A y grupo B. Por ejemplo, si utilizamos M1 para dividir las muestras en el nodo raíz, obtenemos las muestras NC2 y C2 en el grupo A y el resto de las muestras NC4, NC3, NC1, C1 en el grupo B.
Sin tener en cuenta la mutación elegida para el nodo raíz, procedemos a colocar las siguientes mejores características que tengan los valores más altos para la ganancia de información o la función phi en los nodos secundarios izquierdo o derecho del árbol de decisión. Una vez que elegimos el nodo raíz y los dos nodos secundarios para el árbol de profundidad = 3, podemos simplemente agregar las hojas. Las hojas representarán la decisión de clasificación final que el modelo ha producido en función de las mutaciones que una muestra tiene o no tiene. El árbol de la izquierda es el árbol de decisión que obtenemos al usar la ganancia de información para dividir los nodos y el árbol de la derecha es lo que obtenemos al usar la función phi para dividir los nodos.


Supongamos ahora que los resultados de la clasificación de ambos árboles se dan utilizando una matriz de confusión .
Matriz de confusión de ganancia de información:
| Predicho: C | Predicho: NC | |
| Actual: C | 1 | 1 |
| Actual: NC | 0 | 4 |
Matriz de confusión de la función phi:
| Predicho: C | Predicho: NC | |
| Actual: C | 2 | 0 |
| Actual: NC | 1 | 3 |
El árbol que utiliza la ganancia de información tiene los mismos resultados que cuando se utiliza la función phi para calcular la precisión. Cuando clasificamos las muestras según el modelo que utiliza la ganancia de información, obtenemos un verdadero positivo, un falso positivo, cero falsos negativos y cuatro verdaderos negativos. Para el modelo que utiliza la función phi, obtenemos dos verdaderos positivos, cero falsos positivos, un falso negativo y tres verdaderos negativos. El siguiente paso es evaluar la eficacia del árbol de decisiones utilizando algunas métricas clave que se analizarán en la sección Evaluación de un árbol de decisiones a continuación. Las métricas que se analizarán a continuación pueden ayudar a determinar los próximos pasos que se deben seguir al optimizar el árbol de decisiones.
Otras técnicas
La información anterior no es el final para construir y optimizar un árbol de decisiones. Existen muchas técnicas para mejorar los modelos de clasificación de árboles de decisiones que construimos. Una de las técnicas es crear nuestro modelo de árbol de decisiones a partir de un conjunto de datos de arranque . El conjunto de datos de arranque ayuda a eliminar el sesgo que se produce al construir un modelo de árbol de decisiones con los mismos datos con los que se prueba el modelo. La capacidad de aprovechar el poder de los bosques aleatorios también puede ayudar a mejorar significativamente la precisión general del modelo que se está construyendo. Este método genera muchas decisiones a partir de muchos árboles de decisiones y cuenta los votos de cada árbol de decisiones para hacer la clasificación final. Existen muchas técnicas, pero el objetivo principal es probar la construcción de su modelo de árbol de decisiones de diferentes maneras para asegurarse de que alcance el nivel de rendimiento más alto posible.
Evaluación de un árbol de decisiones
Es importante conocer las mediciones utilizadas para evaluar los árboles de decisión. Las métricas principales utilizadas son exactitud , sensibilidad , especificidad , precisión , tasa de error , tasa de falso descubrimiento y tasa de falsa omisión . Todas estas mediciones se derivan de la cantidad de verdaderos positivos , falsos positivos , verdaderos negativos y falsos negativos obtenidos al ejecutar un conjunto de muestras a través del modelo de clasificación del árbol de decisión. Además, se puede crear una matriz de confusión para mostrar estos resultados. Todas estas métricas principales dicen algo diferente sobre las fortalezas y debilidades del modelo de clasificación creado en función de su árbol de decisión. Por ejemplo, una baja sensibilidad con alta especificidad podría indicar que el modelo de clasificación creado a partir del árbol de decisión no identifica bien las muestras de cáncer en comparación con las muestras que no son de cáncer.
Tomemos la matriz de confusión que se muestra a continuación. La matriz de confusión nos muestra que el clasificador del modelo de árbol de decisión creado arrojó 11 verdaderos positivos, 1 falso positivo, 45 falsos negativos y 105 verdaderos negativos.
| Predicho: C | Predicho: NC | |
| Actual: C | 11 | 45 |
| Actual: NC | 1 | 105 |
Ahora calcularemos los valores de precisión, sensibilidad, especificidad, precisión, tasa de errores, tasa de falsos descubrimientos y tasa de falsas omisiones.
Exactitud:
Sensibilidad (TPR – tasa de verdaderos positivos): [14]
Especificidad (TNR – tasa de verdaderos negativos):
Precisión (PPV – valor predictivo positivo):
Tasa de errores (FNR – tasa de falsos negativos):
Tasa de falsos descubrimientos (FDR):
Tasa de falsas omisiones (FOR):
Una vez que hemos calculado las métricas clave, podemos sacar algunas conclusiones iniciales sobre el rendimiento del modelo de árbol de decisiones construido. La precisión que calculamos fue del 71,60 %. El valor de precisión es bueno para empezar, pero nos gustaría que nuestros modelos fueran lo más precisos posible manteniendo el rendimiento general. El valor de sensibilidad del 19,64 % significa que de todos los que dieron positivo en la prueba de cáncer, dieron positivo. Si observamos el valor de especificidad del 99,06 %, sabemos que de todas las muestras que dieron negativo en la prueba de cáncer, dieron negativo. Cuando se trata de sensibilidad y especificidad, es importante tener un equilibrio entre los dos valores, por lo que si podemos disminuir nuestra especificidad para aumentar la sensibilidad, eso resultaría beneficioso. [15] Estos son solo algunos ejemplos de cómo utilizar estos valores y los significados detrás de ellos para evaluar el modelo de árbol de decisiones y mejorar la próxima iteración.
Véase también
- Árbol de comportamiento (inteligencia artificial, robótica y control) – Modelo matemático de ejecución de planes
- Impulso (aprendizaje automático) : método en el aprendizaje automático
- Ciclo de decisión – Secuencia de pasos para la toma de decisiones
- Lista de decisiones
- Matriz de decisión
- Tabla de decisiones : tabla que especifica acciones basadas en condiciones
- Modelo de árbol de decisión : modelo de complejidad computacional del cálculo
- Fundamento del diseño : documentación explícita de las razones detrás de las decisiones tomadas al diseñar un sistema o artefacto.Pages displaying wikidata descriptions as a fallback
- DRAKON – Herramienta de mapeo de algoritmos
- Cadena de Markov : proceso aleatorio independiente del historial
- Bosque aleatorio : método de aprendizaje automático por conjuntos basado en árboles
- Enfoque de prioridad ordinal – Método de análisis de decisiones con criterios múltiples
- Algoritmo de probabilidades : método para calcular estrategias óptimas para problemas de último éxito
- Combinatoria topológica
- Tabla de verdad : tabla matemática utilizada en lógica
Referencias
- ^ von Winterfeldt, Detlof; Edwards, Ward (1986). "Árboles de decisión". Análisis de decisiones e investigación del comportamiento . Cambridge University Press. págs. 63–89. ISBN 0-521-27304-8.
- ^ Kamiński, B.; Jakubczyk, M.; Szufel, P. (2017). "Un marco para el análisis de sensibilidad de árboles de decisión". Revista centroeuropea de investigación de operaciones . 26 (1): 135–159. doi :10.1007/s10100-017-0479-6. PMC 5767274 . PMID 29375266.
- ^ Xu, Ningzhe; Lovreglio, Ruggiero; Kuligowski, Erica D.; Cova, Thomas J.; Nilsson, Daniel; Zhao, Xilei (1 de marzo de 2023). "Predicción y evaluación de la toma de decisiones de evacuación por incendios forestales mediante aprendizaje automático: hallazgos del incendio Kincade de 2019". Tecnología contra incendios . 59 (2): 793–825. doi :10.1007/s10694-023-01363-1. ISSN 1572-8099.
- ^ Díaz-Ramírez, Jenny; Estrada-García, Juan Alberto; Figueroa-Sayago, Juliana (1 de diciembre de 2023). "Predicción de las preferencias de elección de modos de transporte en un distrito universitario con modelos basados en árboles de decisión". Interacciones entre la ciudad y el medio ambiente . 20 : 100118. doi : 10.1016/j.cacint.2023.100118 . ISSN 2590-2520.
- ^ Quinlan, JR (1987). "Simplificación de árboles de decisión". Revista internacional de estudios hombre-máquina . 27 (3): 221–234. CiteSeerX 10.1.1.18.4267 . doi :10.1016/S0020-7373(87)80053-6.
- ^ K. Karimi y HJ Hamilton (2011), "Generación e interpretación de reglas de decisión temporal", Revista internacional de sistemas de información informática y aplicaciones de gestión industrial, volumen 3
- ^ Wagner, Harvey M. (1 de septiembre de 1975). Principios de investigación de operaciones: con aplicaciones a las decisiones gerenciales (2.ª ed.). Englewood Cliffs, NJ: Prentice Hall. ISBN 9780137095926.
- ^ R. Quinlan, "Aprendizaje de procedimientos de clasificación eficientes", Machine Learning: an artificial intelligence approach , Michalski, Carbonell & Mitchell (eds.), Morgan Kaufmann, 1983, pág. 463–482. doi :10.1007/978-3-662-12405-5_15
- ^ Utgoff, PE (1989). Inducción incremental de árboles de decisión. Aprendizaje automático, 4(2), 161–186. doi :10.1023/A:1022699900025
- ^ Deng, H.; Runger, G.; Tuv, E. (2011). Medidas de sesgo de importancia para atributos y soluciones multivaluados. Actas de la 21.ª Conferencia Internacional sobre Redes Neuronales Artificiales (ICANN).
- ^ Larose, Chantal, Daniel (2014). Descubrimiento de conocimiento en los datos . Hoboken, NJ: John Wiley & Sons. p. 167. ISBN 9780470908747.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Plapinger, Thomas (29 de julio de 2017). «¿Qué es un árbol de decisiones?». Towards Data Science . Archivado desde el original el 10 de diciembre de 2021. Consultado el 5 de diciembre de 2021 .
- ^ Tao, Christopher (6 de septiembre de 2020). "No utilice el árbol de decisiones de esta manera". Towards Data Science . Archivado desde el original el 10 de diciembre de 2021. Consultado el 10 de diciembre de 2021 .
- ^ "Tasa de falsos positivos | Glosario de Split". Split . Consultado el 10 de diciembre de 2021 .
- ^ "Sensibilidad vs. especificidad". Análisis y separaciones de Technology Networks . Consultado el 10 de diciembre de 2021 .
Enlaces externos
- Amplios tutoriales y ejemplos de árboles de decisión
- Galería de ejemplos de árboles de decisión
- Árboles de decisión potenciados por gradiente

















