Razonamiento diagramático

Mapeo de información
Temas y campos
Mapeo de decisiones empresariales Visualización de datos Comunicación gráfica Infografías Diseño de información Visualización del conocimiento Modelo mental Análisis morfológico Ontología (ciencia de la información) Esquema (psicología) Analítica visual Lenguaje visual
Enfoques de nodo-enlace
Mapa de argumentos Cladística Mapa cognitivo Concepto de red Mapa conceptual Gráfico conceptual Árbol de decisiones Dendrograma Dibujo gráfico Árbol hiperbólico Hipertexto Mapa de problemas Árbol de problemas Dibujo de gráficos en capas Mapa mental Modelado de objetos y roles Organigrama Red Pathfinder Árbol radial Red semántica Sociograma Cronología Mapa de temas Estructura de árbol Zigzag
Véase también
Fundamento del diseño Razonamiento diagramático Modelo entidad-relación Geovisualización Lista de software de creación de mapas conceptuales y mentales Olog Ontología (filosofía) Métodos de estructuración de problemas Web semántica Mapeo de árboles Problema perverso
en a mi

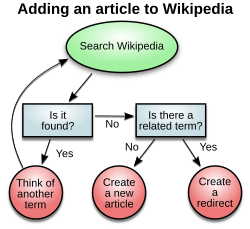
El razonamiento diagramático es el razonamiento por medio de representaciones visuales . El estudio del razonamiento diagramático trata sobre la comprensión de conceptos e ideas, visualizados mediante el uso de diagramas e imágenes en lugar de medios lingüísticos o algebraicos .

Un diagrama es una representación simbólica geométrica en 2D de información según alguna técnica de visualización . En ocasiones, la técnica utiliza una visualización en 3D que luego se proyecta sobre la superficie 2D. El término diagrama en el sentido común puede tener dos significados:

• Dispositivo de información visual : Al igual que el término " ilustración ", el diagrama se utiliza como un término colectivo que representa toda la clase de géneros técnicos, incluidos gráficos , dibujos técnicos y tablas . ^[1]
• tipo específico de presentación visual : este es solo el género que muestra datos cualitativos con formas conectadas por líneas, flechas u otros enlaces visuales.

En el ámbito científico, el término se utiliza de ambas maneras. Por ejemplo, Anderson (1997) afirmó de forma más general que "los diagramas son representaciones gráficas, aunque abstractas, de información, y los mapas , los gráficos de líneas , los diagramas de barras , los planos de ingeniería y los bocetos de los arquitectos son ejemplos de diagramas, mientras que las fotografías y los vídeos no lo son". ^[2] Por otra parte, Lowe (1993) definió los diagramas específicamente como "representaciones gráficas abstractas del tema que representan". ^[3]

En sentido específico, los diagramas y gráficos contrastan con los gráficos de computadora , las ilustraciones técnicas, las infografías , los mapas y los dibujos técnicos , al mostrar "representaciones abstractas en lugar de literales de la información". ^[1] Las esencias de un diagrama pueden verse como: ^[1]

• una forma de dispositivos de formato visual
• una pantalla que no muestra datos cuantitativos , sino relaciones e información abstracta
• con bloques de construcción como formas geométricas que están conectadas por líneas, flechas u otros enlaces visuales.

O como escribió Bert S. Hall, "los diagramas son figuras simplificadas, caricaturas en cierto modo, destinadas a transmitir un significado esencial". ^[4] Según Jan V. White (1984), "las características de un buen diagrama son la elegancia, la claridad, la facilidad, el patrón, la simplicidad y la validez". ^[1] Para White, la elegancia significa que lo que se ve en el diagrama es "la solución más simple y adecuada a un problema". ^[5]

Un gráfico lógico es un tipo especial de estructura de teoría de gráficos en cualquiera de varios sistemas de sintaxis gráfica que Charles Sanders Peirce desarrolló para la lógica .

En sus artículos sobre lógica cualitativa , grafos entitativos y grafos existenciales , Peirce desarrolló varias versiones de un formalismo gráfico, o un lenguaje formal de teoría de grafos , diseñado para ser interpretado por la lógica.

En el siglo transcurrido desde que Peirce inició esta línea de desarrollo, una variedad de sistemas formales se han ramificado a partir de lo que es abstractamente la misma base formal de estructuras de teoría de grafos.

Un grafo conceptual (CG) es una notación para lógica basada en los grafos existenciales de Charles Sanders Peirce y las redes semánticas de inteligencia artificial . En el primer artículo publicado sobre grafos conceptuales, John F. Sowa los utilizó para representar los esquemas conceptuales utilizados en los sistemas de bases de datos. Su primer libro ^[6] los aplicó a una amplia gama de temas en inteligencia artificial, informática y ciencia cognitiva. Una notación lineal, llamada Formato de Intercambio de Gráficos Conceptuales (CGIF) , se ha estandarizado en el estándar ISO para Lógica Común .

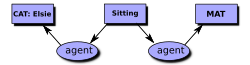
El diagrama de la derecha es un ejemplo de la forma de visualización de un gráfico conceptual. Cada cuadro se denomina nodo de concepto y cada óvalo se denomina nodo de relación . En CGIF, este CG se representaría con la siguiente declaración:

[Gata Elsie] [Sentada *x] [Mat *y] (agente ?x Elsie) (ubicación ?x ?y)

En CGIF, los corchetes encierran la información dentro de los nodos de concepto, y los paréntesis encierran la información dentro de los nodos de relación. Las letras x e y, que se denominan etiquetas de correferencia , muestran cómo se conectan los nodos de concepto y relación. En el formato de intercambio lógico común (CLIF) , esas letras se asignan a variables, como en la siguiente declaración:

(existe ((x Sentado) (y Mat)) (y (Gata Elsie) (agente x Elsie) (ubicación xy)))

Como muestra este ejemplo, los asteriscos en las etiquetas de correferencia *x e *y en CGIF corresponden a variables cuantificadas existencialmente en CLIF, y los signos de interrogación en ?x e ?y corresponden a variables ligadas en CLIF. Un cuantificador universal, representado @every*z en CGIF, se representaría como forall (z) en CLIF.

Un grafo entitativo es un elemento de la sintaxis gráfica para la lógica que Charles Sanders Peirce desarrolló bajo el nombre de lógica cualitativa a partir de la década de 1880, tomando la cobertura del formalismo solo en lo que respecta a los aspectos proposicionales o oracionales de la lógica. ^[7]

La sintaxis es:

• La página en blanco;
• Letras sueltas, frases;
• Objetos (subgrafos) encerrados en una curva cerrada simple llamada corte . Un corte puede estar vacío.

La semántica es:

• La página en blanco denota Falso ;
• Las letras, frases, subgráficos y gráficos completos pueden ser Verdaderos o Falso ;
• Rodear objetos con un corte es equivalente a la complementación booleana . Por lo tanto, un corte vacío denota Verdad ;
• Todos los objetos dentro de un corte dado están unidos tácitamente por disyunción .

Una "prueba" manipula un gráfico, utilizando una lista corta de reglas, hasta que el gráfico se reduce a un corte vacío o a una página en blanco. Un gráfico que se puede reducir de esta manera es lo que ahora se llama una tautología (o su complemento). Los gráficos que no se pueden simplificar más allá de cierto punto son análogos de las fórmulas satisfacibles de la lógica de primer orden .

Un gráfico existencial es un tipo de notación diagramática o visual para expresiones lógicas, propuesta por Charles Sanders Peirce , quien escribió su primer artículo sobre lógica gráfica en 1882 y continuó desarrollando el método hasta su muerte en 1914. Peirce propuso tres sistemas de gráficos existenciales:

• alfa – isomorfo a la lógica oracional y al álgebra booleana de dos elementos ;
• beta – isomorfo a la lógica de primer orden con identidad, con todas las fórmulas cerradas;
• gamma – (casi) isomorfo a la lógica modal normal .

Alfa se anida en beta y gamma . Beta no se anida en gamma , siendo la lógica modal cuantificada algo más de lo que Peirce podría imaginar.

En alfa la sintaxis es:

• La página en blanco;
• Letras o frases sueltas escritas en cualquier parte de la página;
• Cualquier gráfico puede estar encerrado en una curva cerrada simple llamada corte o sep . Un corte puede estar vacío. Los cortes pueden anidarse y concatenarse a voluntad, pero nunca deben intersecarse.

Cualquier parte bien formada de un gráfico es un subgráfico .

La semántica es:

• La página en blanco denota la Verdad ;
• Las letras, frases, subgráficos y gráficos completos pueden ser Verdaderos o Falso ;
• Encerrar un subgrafo con un corte es equivalente a una negación lógica o complementación booleana . Por lo tanto, un corte vacío denota Falso .
• Todos los subgrafos dentro de un corte dado están tácitamente unidos .

Por lo tanto, los grafos alfa son una notación minimalista para la lógica oracional , basada en la adecuación expresiva de And y Not . Los grafos alfa constituyen una simplificación radical del álgebra booleana de dos elementos y los funtores de verdad .

Characteristica universalis , comúnmente interpretada como característica universal o carácter universal en español, es un lenguaje universal y formal imaginado por el filósofo alemán Gottfried Leibniz capaz de expresar conceptos matemáticos, científicos y metafísicos. Leibniz esperaba así crear un lenguaje utilizable en el marco de un cálculo lógico universal o calculus ratiocinator .

Dado que la characteria universalis es diagramática y emplea pictogramas (abajo a la izquierda), los diagramas de la obra de Leibniz merecen un estudio minucioso. En al menos dos ocasiones, Leibniz ilustró su razonamiento filosófico con diagramas. Uno de ellos, el frontispicio de su De Arte Combinatoria (Sobre el arte de las combinaciones) de 1666, representa la teoría aristotélica de cómo todas las cosas materiales se forman a partir de combinaciones de los elementos tierra, agua, aire y fuego.

Estos cuatro elementos forman las cuatro esquinas de un diamante (ver la imagen de la derecha). Los pares opuestos de estos elementos están unidos por una barra rotulada "contrarios" (tierra-aire, fuego-agua). En las cuatro esquinas del cuadrado superpuesto están las cuatro cualidades que definen los elementos. Cada par adyacente de estos elementos está unido por una barra rotulada "combinación posible"; las diagonales que los unen están rotuladas "combinación imposible". Empezando desde arriba, el fuego se forma a partir de la combinación de sequedad y calor; el aire a partir de humedad y calor; el agua a partir de frío y humedad; la tierra a partir de frío y sequedad. ^[8]

A principios de los años 1990, Sun-Joo Shin presentó una extensión de los grafos existenciales llamada Venn-II. ^[9] La sintaxis y la semántica se dan formalmente, junto con un conjunto de reglas de transformación que se demuestra que son sólidas y completas. Las demostraciones se realizan aplicando las reglas (que eliminan o añaden elementos sintácticos a los diagramas o desde ellos) de forma secuencial. Venn-II es equivalente en poder expresivo a un lenguaje monádico de primer orden.

• Gerard Allwein y Jon Barwise (ed.) (1996). Razonamiento lógico con diagramas. Oxford University Press.
• Michael Anderson, Peter Cheng, Volker Haarslev (Eds.) (2000). Teoría y aplicación de diagramas: Primera conferencia internacional, Diagrams 2000. Edimburgo, Escocia, Reino Unido, 1 al 3 de septiembre de 2000. Actas.
• Michael Anderson y R. McCartney (2003). Procesamiento de diagramas: computación con diagramas. En: Inteligencia artificial , volumen 145, número 1-2, abril de 2003.
• James Robert Brown (1999). Filosofía de las matemáticas: Introducción al mundo de las pruebas y las imágenes. Routledge.
• James Franklin (2000). Razonamiento diagramático y modelado en la imaginación: las armas secretas de la Revolución científica, en 1543 y todo eso: imagen y palabra, cambio y continuidad en la revolución protocientífica , ed. G. Freeland y A. Corones (Kluwer, Dordrecht), págs. 53-115.
• Janice Glasgow, N. Hari Narayanan y B. Chandrasekaran (ed.) (1995). Razonamiento diagramático: perspectivas cognitivas y computacionales. AAAI Press.
• Kulpa, Zenon . "Representación diagramática y razonamiento". Machine GRAPHICS & VISION 3 (1/2. 1994.
• Gem Stapleton Un estudio de los sistemas de razonamiento basados ​​en diagramas de Euler ^{[ enlace muerto permanente ]} . Notas electrónicas sobre informática teórica. 2005.

• Sitio de razonamiento diagramático Archivado el 19 de junio de 2009 en Wayback Machine desde la Universidad de Hartford, Connecticut, EE. UU.
• Conferencia sobre Álgebra Universal y Razonamiento Diagramático por John Baez, 3 de febrero de 2006.
• Grupo de Modelado Visual en la Universidad de Brighton, Reino Unido.
• Diagramas de Marlo en línea para resolver silogismos.