Prisma hexagonal

Prisma con base de 6 lados

Prisma hexagonal uniforme

Tipo	Poliedro prismático uniforme
Elementos	F = 8, E = 18, V = 12 (χ = 2)
Caras por lados	6{4}+2{6}
Símbolo de Schläfli	t{2,6} o {6}×{}
Símbolo de Wythoff	2 6 \| 2 2 2 3 \|
Diagramas de Coxeter
Simetría	D _6h , [6,2], (*622), orden 24
Grupo de rotación	D ₆ , [6,2] ⁺ , (622), orden 12
Referencias	U _76(d)
Dual	Bipirámide hexagonal
Propiedades	convexo , zonóedro
Figura de vértice 4.4.6

En geometría , el prisma hexagonal es un prisma con base hexagonal . Los prismas son poliedros ; este poliedro tiene 8 caras , 18 aristas y 12 vértices . ^[1]

Dado que tiene 8 caras, es un octaedro . Sin embargo, el término octaedro se utiliza principalmente para referirse al octaedro regular , que tiene ocho caras triangulares. Debido a la ambigüedad del término octaedro y la tilaridad de las diversas figuras de ocho lados, el término rara vez se utiliza sin una aclaración.

Antes de afilarse, muchos lápices toman la forma de un prisma hexagonal largo. ^[2]

Como un poliedro semirregular (o uniforme)

Si todas las caras son regulares, el prisma hexagonal es un poliedro semirregular , más generalmente, un poliedro uniforme , y el cuarto en un conjunto infinito de prismas formados por lados cuadrados y dos tapas de polígonos regulares. Puede verse como un hosoedro hexagonal truncado , representado por el símbolo de Schläfli t{2,6}. Alternativamente, puede verse como el producto cartesiano de un hexágono regular y un segmento de línea , y representado por el producto {6}×{}. El dual de un prisma hexagonal es una bipirámide hexagonal .

El grupo de simetría de un prisma hexagonal recto es D _6h de orden 24. El grupo de rotación es D ₆ de orden 12.

Volumen

Como en la mayoría de los prismas, el volumen se obtiene tomando el área de la base, con una longitud de lado de , y multiplicándola por la altura , obteniéndose la fórmula: ^[3] ${\estilo de visualización a}$ ${\estilo de visualización h}$

$V={\frac {3{\sqrt {3}}}{2}}a^{2}\times h$ y su área de superficie puede ser . $S=3a({\sqrt {3}}a+2h)$

Simetría

La topología de un prisma hexagonal uniforme puede tener variaciones geométricas de menor simetría, entre ellas:

Simetría	D _6h , [2,6], (*622)	C _6v , [6], (*66)	D _3h , [2,3], (*322)		D _3d , [2 ⁺ ,6], (2*3)
Nombre	Prisma hexagonal regular	Tronco hexagonal	Prisma ditrigonal	Prisma triámbico	Trapezoprisma ditrigonal
Construcción	{6}×{},		t{3}×{},		y ₂ {2,6},
Imagen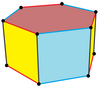
Distorsión

Como parte de teselaciones espaciales

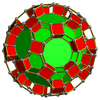
Existe como celdas de cuatro panales prismáticos uniformes convexos en 3 dimensiones:

Panal prismático hexagonal ^[1]	Panal prismático triangular-hexagonal	Panal prismático triangular-hexagonal de forma chata	Panal prismático rombitriangular-hexagonal

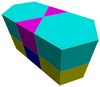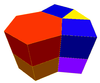También existe como células de una serie de 4-politopos uniformes de cuatro dimensiones , entre los que se incluyen:

Poliedros y teselaciones relacionados

Poliedros esféricos diedros hexagonales uniformes
Simetría : [6,2] , (*622)							[6,2] ⁺ , (622)	[6,2 ⁺ ], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
De duales a uniformes

V6 ²	V12 ²	V6 ²	V4.4.6	Versión 2 ⁶	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Este poliedro puede considerarse miembro de una secuencia de patrones uniformes con figura de vértice (4.6.2p) y diagrama de Coxeter-Dynkin. Para p < 6, los miembros de la secuencia son poliedros omnitruncados ( zonoedros ), que se muestran a continuación como teselas esféricas. Para p > 6, son teselas del plano hiperbólico, comenzando con la tesela triheptagonal truncada .

* n 32 mutación de simetría de teselaciones omnitruncadas: 4.6.2n en a mi
Sím. * n 32 [ n ,3]	Esférico				Euclides.	Hiperb. compacta.		Paraíso.	Hiperbólica no compacta
Sím. * n 32 [ n ,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Cifras
Configuración.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duales
Configuración.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	Versión 4.6.24i	Versión 4.6.18i	Versión 4.6.12i	Versión 4.6.6i

Véase también

Familia de prismas n- gonales uniformes en a mi
Nombre del prisma	Prisma digonal	Prisma triangular (trigonal)	Prisma cuadrado (tetragonal)	Prisma pentagonal	Prisma hexagonal	Prisma heptagonal	Prisma octogonal	Prisma eneágonal	Prisma decagonal	Prisma hendecagonal	Prisma dodecagonal	...	Prisma apeirogonal
Imagen de poliedro												...
Imagen de mosaico esférico												Imagen de mosaico plano
Configuración de vértice.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Diagrama de Coxeter												...

Referencias

^ ab Pugh, Anthony (1976), Poliedros: un enfoque visual, University of California Press, págs. 21, 27, 62, ISBN 9780520030565.
^ Simpson, Audrey (2011), Matemáticas básicas para Cambridge IGCSE, Cambridge University Press, págs. 266-267, ISBN 9780521727921.
^ Wheater, Carolyn C. (2007), Geometría , Career Press, págs. 236-237, ISBN 9781564149367

Enlaces externos

Panales uniformes en modelos VRML de 3 espacios
Los poliedros uniformes
Poliedros de realidad virtual La enciclopedia de poliedros Prismas y antiprismas
Weisstein, Eric W. "Prisma hexagonal". MathWorld .
Modelo interactivo de prisma hexagonal: funciona en su navegador web

Este artículo relacionado con el poliedro es un esbozo . Puedes ayudar a Wikipedia expandiéndolo.

[pugh-1] Pugh, Anthony (1976), Poliedros: un enfoque visual, University of California Press, págs. 21, 27, 62, ISBN 9780520030565.

[2] Simpson, Audrey (2011), Matemáticas básicas para Cambridge IGCSE, Cambridge University Press, págs. 266-267, ISBN 9780521727921.

[3] Wheater, Carolyn C. (2007), Geometría , Career Press, págs. 236-237, ISBN 9781564149367

prisma tetraédrico truncado	prisma octaédrico truncado	Prisma cuboctaédrico truncado	Prisma icosaédrico truncado	Prisma icosidodecaédrico truncado

Runcitruncado de 5 celdas	omnitruncado de 5 celdas	Runcitruncado de 16 celdas	teseracto omnitruncado

Runcitruncado de 24 celdas	omnitruncado de 24 celdas	Runcitruncado de 600 celdas	omnitruncado de 120 celdas