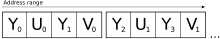YCbCr

YCbCr , Y′CbCr o Y Pb/Cb Pr/Cr , también escrito como YC _B C _R o Y′C _B C _R , es una familia de espacios de color utilizados como parte de la cadena de procesamiento de imágenes en color en sistemas de vídeo y fotografía digital . Y′ es el componente de luminancia y C _B y C _R son los componentes de croma de diferencia de azul y diferencia de rojo . Y′ (con prima ) se distingue de Y, que es luminancia , lo que significa que la intensidad de la luz se codifica de forma no lineal en función de los primarios RGB corregidos por gamma .

Los espacios de color Y′CbCr se definen mediante una transformación matemática de coordenadas a partir de los primarios RGB asociados y el punto blanco. Si el espacio de color RGB subyacente es absoluto, el espacio de color Y′CbCr también es un espacio de color absoluto ; por el contrario, si el espacio RGB está mal definido, también lo está Y′CbCr. La transformación se define en las ecuaciones 32, 33 de la norma ITU-T H.273. Sin embargo, esa regla no se aplica a los primarios P3-D65 utilizados por Netflix con la matriz BT.2020-NCL, por lo que significa que la matriz no se derivó de los primarios, pero ahora Netflix permite los primarios BT.2020 (desde 2021). ^[1] Lo mismo ocurre con JPEG: tiene una matriz BT.601 derivada de los primarios System M, pero los primarios de la mayoría de las imágenes son BT.709.

Las pantallas de tubos de rayos catódicos funcionan con señales de voltaje rojo, verde y azul, pero estas señales RGB no son eficientes como representación para almacenamiento y transmisión, ya que tienen mucha redundancia .

YCbCr e Y′CbCr son una aproximación práctica al procesamiento del color y la uniformidad perceptual, donde los colores primarios que corresponden aproximadamente al rojo, verde y azul se procesan para obtener información perceptualmente significativa. Al hacer esto, el procesamiento, la transmisión y el almacenamiento de imágenes y videos posteriores pueden realizar operaciones e introducir errores de maneras perceptualmente significativas. Y′CbCr se utiliza para separar una señal de luminancia (Y′) que se puede almacenar con alta resolución o transmitir con un ancho de banda alto, y dos componentes de croma (C _B y C _R ) que se pueden reducir en ancho de banda, submuestrear, comprimir o tratar de otro modo por separado para mejorar la eficiencia del sistema.

Un ejemplo práctico sería reducir el ancho de banda o la resolución asignada al "color" en comparación con el "blanco y negro", ya que los humanos son más sensibles a la información en blanco y negro (ver ejemplo de imagen a la derecha). Esto se denomina submuestreo de croma .

En ocasiones, YCbCr se abrevia como YCC . Normalmente, los términos Y′CbCr, YCbCr, YPbPr y YUV se utilizan indistintamente, lo que genera cierta confusión. La principal diferencia es que YPbPr se utiliza con imágenes analógicas y YCbCr con imágenes digitales, lo que genera diferentes valores de escala para Umax _y Vmax ₍ en YCbCr ambos son ) al convertir a/desde YUV. Y′CbCr y YCbCr difieren debido a que los valores están corregidos por gamma o no. ${\displaystyle {\frac {1}{2}}}$

Las ecuaciones siguientes ofrecen una mejor idea de los principios comunes y las diferencias generales entre estos formatos.

Las señales Y′CbCr (antes del escalado y las compensaciones para colocar las señales en formato digital) se denominan YPbPr y se crean a partir de la fuente RGB (rojo, verde y azul) ajustada por gamma correspondiente utilizando tres constantes definidas K _R , K _G y K _B de la siguiente manera:

${\displaystyle {\begin{aligned}Y'&=K_{R}\cdot R'+K_{G}\cdot G'+K_{B}\cdot B'\\P_{B}&={\frac {1}{2}}\cdot {\frac {B'-Y'}{1-K_{B}}}\\P_{R}&={\frac {1}{2}}\cdot {\frac {R'-Y'}{1-K_{R}}}\end{aligned}}}$

donde K _R , K _G y K _B se derivan ordinariamente de la definición del espacio RGB correspondiente y se requiere que satisfagan . ${\displaystyle K_{R}+K_{G}+K_{B}=1}$

La manipulación de la matriz equivalente a menudo se denomina "matriz de color":

${\displaystyle {\begin{bmatrix}Y'\\P_{B}\\P_{R}\end{bmatrix}}={\begin{bmatrix}K_{R}&K_{G}&K_{B}\\-{\frac {1}{2}}\cdot {\frac {K_{R}}{1-K_{B}}}&-{\frac {1}{2}}\cdot {\frac {K_{G}}{1-K_{B}}}&{\frac {1}{2}}\\{\frac {1}{2}}&-{\frac {1}{2}}\cdot {\frac {K_{G}}{1-K_{R}}}&-{\frac {1}{2}}\cdot {\frac {K_{B}}{1-K_{R}}}\end{bmatrix}}{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}}$

Y su inversa:

${\displaystyle {\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}={\begin{bmatrix}1&0&2-2\cdot K_{R}\\1&-{\frac {K_{B}}{K_{G}}}\cdot (2-2\cdot K_{B})&-{\frac {K_{R}}{K_{G}}}\cdot (2-2\cdot K_{R})\\1&2-2\cdot K_{B}&0\end{bmatrix}}{\begin{bmatrix}Y'\\P_{B}\\P_{R}\end{bmatrix}}}$

Aquí, los símbolos primos (′) significan que se está utilizando la corrección gamma ; por lo tanto, R′, G′ y B′ varían nominalmente de 0 a 1, donde 0 representa la intensidad mínima (por ejemplo, para la visualización del color negro ) y 1 la máxima (por ejemplo, para la visualización del color blanco ). El valor de luminancia (Y) resultante tendrá entonces un rango nominal de 0 a 1, y los valores de croma (P _B y P _R ) tendrán un rango nominal de -0,5 a +0,5. El proceso de conversión inversa se puede derivar fácilmente invirtiendo las ecuaciones anteriores.

Al representar las señales en forma digital, los resultados se escalan y redondean, y normalmente se añaden compensaciones. Por ejemplo, la escala y la compensación aplicadas al componente Y′ según la especificación (por ejemplo, MPEG-2 ^[2] ) dan como resultado el valor 16 para el negro y el valor 235 para el blanco cuando se utiliza una representación de 8 bits. El estándar tiene versiones digitalizadas de 8 bits de C _B y C _R escaladas a un rango diferente de 16 a 240. En consecuencia, a veces se requiere un reescalado por la fracción (235-16)/(240-16) = 219/224 cuando se realiza un procesamiento o matrizado de color en el espacio YCbCr, lo que da como resultado distorsiones de cuantificación cuando el procesamiento posterior no se realiza utilizando profundidades de bits más altas.

El escalamiento que resulta en el uso de un rango menor de valores digitales que lo que parecería deseable para la representación del rango nominal de los datos de entrada permite cierto "sobreimpulso" y "subimpulso" durante el procesamiento sin necesidad de un recorte indeseable . Este " margen de maniobra " y "margen de tolerancia" ^{[3] también se puede utilizar para la extensión de la} gama de colores nominal , como se especifica en xvYCC .

El valor 235 admite un sobreimpulso máximo de (255 - 235) / (235 - 16) = 9,1 %, que es ligeramente mayor que el sobreimpulso máximo teórico ( fenómeno de Gibbs ) de aproximadamente el 8,9 % del paso máximo (de negro a blanco). El margen de transición es menor, permitiendo solo un sobreimpulso de 16 / 219 = 7,3 %, que es menor que el sobreimpulso máximo teórico del 8,9 %. Además, debido a que los valores 0 y 255 están reservados en HDMI, el margen es en realidad ligeramente menor.

Dado que las ecuaciones que definen Y′CbCr se forman de una manera que rota todo el cubo de color RGB nominal y lo escala para que encaje dentro de un cubo de color YCbCr (más grande), hay algunos puntos dentro del cubo de color Y′CbCr que no se pueden representar en el dominio RGB correspondiente (al menos no dentro del rango RGB nominal). Esto causa cierta dificultad a la hora de determinar cómo interpretar y mostrar correctamente algunas señales Y′CbCr. Estos valores Y′CbCr fuera de rango son utilizados por xvYCC para codificar colores fuera de la gama BT.709.

La forma de Y′CbCr que se definió para el uso en televisión de definición estándar en la norma ITU-R BT.601 (anteriormente CCIR 601 ) para su uso con vídeo de componentes digitales se deriva del espacio RGB correspondiente (primarios del Sistema M de la ITU-R BT.470-6) de la siguiente manera:

${\displaystyle {\begin{aligned}K_{R}&=0,299\\K_{G}&=0,587\\K_{B}&=0,114\end{aligned}}}$

De las constantes y fórmulas anteriores, se puede derivar lo siguiente para ITU-R BT.601.

El YPbPr analógico del R'G'B' analógico se deriva de la siguiente manera:

${\displaystyle {\begin{aligned}Y'&=&0.299\cdot R'&+&0.587\cdot G'&+&0.114\cdot B'\\P_{B}&=-&0.168736\cdot R'&-&0.331264\cdot G'&+&0.5\cdot B'\\P_{R}&=&0.5\cdot R'&-&0.418688\cdot G'&-&0.081312\cdot B'\end{aligned}}}$

El Y′CbCr digital (8 bits por muestra) se deriva del R'G'B' analógico de la siguiente manera:

${\displaystyle {\begin{aligned}Y'&=&16&+&(65.481\cdot R'&+&128.553\cdot G'&+&24.966\cdot B')\\C_{B}&=&128&+&(-37.797\cdot R'&-&74.203\cdot G'&+&112.0\cdot B')\\C_{R}&=&128&+&(112.0\cdot R'&-&93.786\cdot G'&-&18.214\cdot B')\end{aligned}}}$

o simplemente por componentes

${\displaystyle {\begin{aligned}(Y',C_{B},C_{R})&=&(16,128,128)+(219\cdot Y,224\cdot P_{B},224\cdot P_{R})\\\end{aligned}}}$

Las señales resultantes varían de 16 a 235 para Y′ (Cb y Cr varían de 16 a 240); los valores de 0 a 15 se denominan footroom , mientras que los valores de 236 a 255 se denominan headroom . Los mismos rangos de cuantificación, diferentes para Y y Cb, Cr también se aplican a BT.2020 y BT.709.

Como alternativa, el Y′CbCr digital se puede derivar del R'dG'dB'd digital (8 bits por muestra, cada uno utilizando el rango completo con cero representando negro y 255 representando blanco) de acuerdo con las siguientes ecuaciones:

${\displaystyle {\begin{aligned}Y'&=&16&+&{\frac {65.481\cdot R'_{D}}{255}}&+&{\frac {128.553\cdot G'_{D}}{255}}&+&{\frac {24.966\cdot B'_{D}}{255}}\\C_{B}&=&128&-&{\frac {37.797\cdot R'_{D}}{255}}&-&{\frac {74.203\cdot G'_{D}}{255}}&+&{\frac {112.0\cdot B'_{D}}{255}}\\C_{R}&=&128&+&{\frac {112.0\cdot R'_{D}}{255}}&-&{\frac {93.786\cdot G'_{D}}{255}}&-&{\frac {18.214\cdot B'_{D}}{255}}\end{aligned}}}$

En la fórmula siguiente, los factores de escala se multiplican por . Esto permite obtener el valor 256 en el denominador, que se puede calcular con un solo desplazamiento de bit .${\displaystyle {\frac {256}{255}}}$

${\displaystyle {\begin{aligned}Y'&=&16&+&{\frac {65.738\cdot R'_{D}}{256}}&+&{\frac {129.057\cdot G'_{D}}{256}}&+&{\frac {25.064\cdot B'_{D}}{256}}\\C_{B}&=&128&-&{\frac {37.945\cdot R'_{D}}{256}}&-&{\frac {74.494\cdot G'_{D}}{256}}&+&{\frac {112.439\cdot B'_{D}}{256}}\\C_{R}&=&128&+&{\frac {112.439\cdot R'_{D}}{256}}&-&{\frac {94.154\cdot G'_{D}}{256}}&-&{\frac {18.285\cdot B'_{D}}{256}}\end{aligned}}}$

Si la fuente digital R'd G'd B'd incluye espacio libre y espacio libre, primero se debe restar el desplazamiento del espacio libre 16 de cada señal y se debe incluir un factor de escala en las ecuaciones.${\displaystyle {\frac {255}{219}}}$

La transformada inversa es:

${\displaystyle {\begin{aligned}R'_{D}&=&{\frac {298.082\cdot Y'}{256}}&&&+&{\frac {408.583\cdot C_{R}}{256}}&-&222.921\\G'_{D}&=&{\frac {298.082\cdot Y'}{256}}&-&{\frac {100.291\cdot C_{B}}{256}}&-&{\frac {208.120\cdot C_{R}}{256}}&+&135.576\\B'_{D}&=&{\frac {298.082\cdot Y'}{256}}&+&{\frac {516.412\cdot C_{B}}{256}}&&&-&276.836\end{aligned}}}$

La transformada inversa sin ningún redondeo (utilizando valores que provienen directamente de la recomendación ITU-R BT.601) es:

${\displaystyle {\begin{aligned}R'_{D}={\frac {255}{219}}\cdot (Y'-16)&&&&&&&+{\frac {255}{224}}\cdot 1.402\cdot (C_{R}-128)\\G'_{D}={\frac {255}{219}}\cdot (Y'-16)&-&{\frac {255}{224}}\cdot 1.772&&\cdot {\frac {0.114}{0.587}}&&\cdot (C_{B}-128)&-{\frac {255}{224}}\cdot 1.402\cdot {\frac {0.299}{0.587}}\cdot (C_{R}-128)\\B'_{D}={\frac {255}{219}}\cdot (Y'-16)&+&{\frac {255}{224}}\cdot 1.772&&&&\cdot (C_{B}-128)\end{aligned}}}$

Esta forma de Y′CbCr se utiliza principalmente en sistemas de televisión de definición estándar más antiguos , ya que utiliza un modelo RGB que se adapta a las características de emisión de fósforo de los CRT más antiguos .

En la norma ITU-R BT.709 se especifica una forma diferente de Y′CbCr, principalmente para su uso en HDTV . La forma más nueva también se utiliza en algunas aplicaciones orientadas a pantallas de ordenador, como sRGB (aunque la matriz utilizada para la forma sRGB de YCbCr, sYCC , sigue siendo BT.601). En este caso, los valores de Kb y Kr difieren, pero las fórmulas para utilizarlos son las mismas. Para ITU-R BT.709, las constantes son:

${\displaystyle {\begin{aligned}K_{B}&=0.0722\\K_{R}&=0.2126\\(K_{G}&=1-K_{B}-K_{R}=0.7152)\end{aligned}}}$

Esta forma de Y′CbCr se basa en un modelo RGB que se ajusta mejor a las características de emisión de fósforo de los CRT más nuevos y otros equipos de visualización modernos. ^{[ cita requerida ]} Las matrices de conversión para BT.709 son las siguientes:

${\displaystyle {\begin{aligned}{\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}&={\begin{bmatrix}0.2126&0.7152&0.0722\\-0.1146&-0.3854&0.5\\0.5&-0.4542&-0.0458\end{bmatrix}}{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}\\{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}&={\begin{bmatrix}1&0&1.5748\\1&-0.1873&-0.4681\\1&1.8556&0\end{bmatrix}}{\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}\end{aligned}}}$

Las definiciones de las señales R', G' y B' también difieren entre BT.709 y BT.601, y difieren dentro de BT.601 dependiendo del tipo de sistema de TV en uso (625 líneas como en PAL y SECAM o 525 líneas como en NTSC ), y difieren aún más en otras especificaciones. En diferentes diseños hay diferencias en las definiciones de las coordenadas de cromaticidad R, G y B, el punto blanco de referencia, el rango de gama admitido, las funciones de precompensación de gamma exactas para derivar R', G' y B' a partir de R, G y B, y en la escala y los desplazamientos que se deben aplicar durante la conversión de R'G'B' a Y'CbCr. Por lo tanto, la conversión adecuada de Y'CbCr de una forma a la otra no es solo una cuestión de invertir una matriz y aplicar la otra. De hecho, cuando Y′CbCr se diseña idealmente, los valores de K _B y K _R se derivan de la especificación precisa de las señales primarias de color RGB, de modo que la señal de luminancia (Y′) se corresponde lo más fielmente posible con una medición de luminancia ajustada por gamma (generalmente basada en las mediciones CIE 1931 de la respuesta del sistema visual humano a los estímulos de color). ^[4]

El estándar ITU-R BT.2020 utiliza la misma función gamma que BT.709. Define: ^[5]

• Luminancia no constante Y'CbCr, similar a las entradas anteriores, excepto con diferentes K _B y K _R .
• Luminancia constante Y'cCbcCrc, una formulación donde Y' es la versión del códec gamma de la luminancia verdadera . ^[5]

Para ambos, los coeficientes derivados de las primarias son:

${\displaystyle {\begin{aligned}K_{B}&=0.0593\\K_{R}&=0.2627\\(K_{G}&=1-K_{B}-K_{R}=0.6780)\end{aligned}}}$

Para NCL, la definición es clásica: ; ; . La conversión de codificación se puede escribir, como es habitual, como una matriz. ^[5] La matriz de decodificación para BT.2020-NCL es la siguiente con 14 decimales:${\displaystyle Y'=0.2627R'+0.6780G'+0.0593B'}$${\displaystyle Cb=(B'-Y')/1.8814}$${\displaystyle Cr=(R'-Y')/1.4746}$

${\displaystyle {\begin{aligned}{\begin{bmatrix}R\\G\\B\end{bmatrix}}&={\begin{bmatrix}1&0&1.4746\\1&-0.16455312684366&-0.57135312684366\\1&1.8814&0\end{bmatrix}}{\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}\end{aligned}}}$

Los valores más pequeños de la matriz no se redondean, sino que son valores precisos. Para sistemas con precisión limitada (8 o 10 bits, por ejemplo), se podría utilizar una precisión menor de la matriz anterior, por ejemplo, conservando sólo 6 dígitos después del punto decimal. ^[6]

La versión CL, YcCbcCrc, codifica: ^[5]

• ${\displaystyle Y'c=(0.2627R+0.6780G+0.0593B)'}$Esta es la función gamma aplicada a la luminancia real calculada a partir de RGB lineal.
• ${\displaystyle Cbc=(B'-Y'c)/(-2Nb)}$En caso contrario , . y son el mínimo y el máximo teóricos correspondientes a la gama. Los valores "prácticos" redondeados son , . La derivación completa se puede encontrar en la recomendación. ^[5]${\displaystyle B'<Y'c}$${\displaystyle (B'-Y'c)/(2Pb)}$${\displaystyle Nb}$${\displaystyle Pb}$${\displaystyle (B'-Y'c)}$${\displaystyle Pb=0.7910}$${\displaystyle Nb=-0.9702}$
• ${\displaystyle Crc=(R'-Y'c)/(-2Nr)}$En caso contrario , . Nuevamente, y son límites teóricos. Los valores redondeados son , .${\displaystyle R'<Y'c}$${\displaystyle (R'-Y'c)/(2Pr)}$${\displaystyle Pr}$${\displaystyle Nr}$${\displaystyle Pr=0.4969}$${\displaystyle Nr=-0.8591}$

La función CL se puede utilizar cuando la conservación de la luminancia es de importancia primordial (véase: Submuestreo de croma § Error de luminancia gamma ), o cuando "existe la expectativa de una mejora en la eficiencia de codificación para la entrega". La especificación hace referencia al Informe ITU-R BT.2246 sobre este tema. ^[5] BT.2246 afirma que CL ha mejorado la eficiencia de compresión y la conservación de la luminancia, pero NCL será más familiar para un personal que haya manejado previamente la mezcla de colores y otras prácticas de producción en HDTV YCbCr. ^[7]

BT.2020 no define PQ ni, por lo tanto, HDR, sino que se define con más detalle en SMPTE ST 2084 y BT.2100 . BT.2100 introducirá el uso de IC _T C _P , un espacio de color semiperceptual derivado de RGB lineal con buena linealidad de tono. Es una "luminancia casi constante". ^[8]

El estándar SMPTE 240M (utilizado en el sistema de televisión HD analógico MUSE ) define YCC con estos coeficientes:

${\displaystyle {\begin{aligned}K_{B}&=0.087\\K_{R}&=0.212\end{aligned}}}$

Los coeficientes se derivan de los primarios y el punto blanco SMPTE 170M, tal como se utilizan en el estándar 240M.

El uso de JPEG por parte de JFIF admite una Rec. 601 modificada Y′CbCr donde Y′, C _B y C _R tienen el rango completo de 8 bits de [0...255]. ^[9] A continuación se muestran las ecuaciones de conversión expresadas con seis dígitos decimales de precisión. (Para ecuaciones ideales, consulte ITU-T T.871. ^[10] ) Tenga en cuenta que para las siguientes fórmulas, el rango de cada entrada (R,G,B) también es el rango completo de 8 bits de [0...255].

${\displaystyle {\begin{aligned}Y'&=&0&+(0.299&\cdot R'_{D})&+(0.587&\cdot G'_{D})&+(0.114&\cdot B'_{D})\\C_{B}&=&128&-(0.168736&\cdot R'_{D})&-(0.331264&\cdot G'_{D})&+(0.5&\cdot B'_{D})\\C_{R}&=&128&+(0.5&\cdot R'_{D})&-(0.418688&\cdot G'_{D})&-(0.081312&\cdot B'_{D})\end{aligned}}}$

Y de vuelta:

${\displaystyle {\begin{aligned}R'_{D}&=&Y'&&&+1.402&\cdot (C_{R}-128)\\G'_{D}&=&Y'&-0.344136&\cdot (C_{B}-128)&-0.714136&\cdot (C_{R}-128)\\B'_{D}&=&Y'&+1.772&\cdot (C_{B}-128)&\end{aligned}}}$

La conversión anterior es idéntica a sYCC cuando la entrada se proporciona como sRGB, excepto que IEC 61966-2-1:1999/Amd1:2003 solo proporciona cuatro dígitos decimales.

JPEG también define un formato "YCCK" de Adobe para la entrada CMYK . En este formato, el valor "K" se pasa tal cual, mientras que CMY se utiliza para derivar YCbCr con la matriz anterior suponiendo , , y . Como resultado, se puede utilizar un conjunto similar de técnicas de submuestreo. ^[11]${\displaystyle R=1-C}$${\displaystyle G=1-M}$${\displaystyle B=1-Y}$

${\displaystyle {\begin{aligned}K_{B}&=0.0713\\K_{R}&=0.2220\end{aligned}}}$

Estos coeficientes no se utilizan y nunca se han utilizado. ^[12]

H.273 también describe sistemas de luminancia constante y no constante que se derivan estrictamente de los primarios y del punto blanco, de modo que no ocurren situaciones como los primarios predeterminados sRGB/BT.709 de JPEG que utilizan la matriz BT.601 (que se deriva del Sistema M BT.470-6).

Antes del desarrollo de los procesadores rápidos de punto flotante SIMD , la mayoría de las implementaciones digitales de RGB → Y′UV utilizaban matemáticas enteras, en particular aproximaciones de punto fijo . La aproximación significa que la precisión de los números utilizados (datos de entrada, datos de salida y valores constantes) es limitada y, por lo tanto, quien utilice esa opción acepta una pérdida de precisión de aproximadamente el último dígito binario, generalmente como compensación por una mayor velocidad de cálculo.

Los valores de Y′ se desplazan y escalan convencionalmente hasta el rango [16, 235] (denominado swing de estudio o "niveles de TV") en lugar de utilizar el rango completo de [0, 255] (denominado swing completo o "niveles de PC"). Esta práctica se estandarizó en SMPTE-125M para dar cabida a sobreimpulsos de señal ("ringing") debido al filtrado. ^[13] Los valores de U y V, que pueden ser positivos o negativos, se suman con 128 para que siempre sean positivos, lo que da un rango de estudio de 16 a 240 para U y V. (Estos rangos son importantes en la edición y producción de vídeo, ya que el uso del rango incorrecto dará como resultado una imagen con negros y blancos "recortados" o una imagen de bajo contraste).

Estas matrices redondean todos los factores a la unidad 1/256 más cercana. Como resultado, solo se forma un valor intermedio de 16 bits para cada componente, y un simple desplazamiento a la derecha con redondeo (x + 128) >> 8puede encargarse de la división. ^[13]

Para estudio-swing:

${\displaystyle {\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}={\frac {1}{256}}{\begin{bmatrix}66&129&25\\-38&-74&112\\112&-94&-18\end{bmatrix}}{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}+{\begin{bmatrix}16\\128\\128\end{bmatrix}}}$

Para el swing completo:

${\displaystyle {\begin{bmatrix}Y'\\C_{B}\\C_{R}\end{bmatrix}}={\frac {1}{256}}{\begin{bmatrix}77&150&29\\-43&-84&127\\127&-106&-21\end{bmatrix}}{\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}+{\begin{bmatrix}0\\128\\128\end{bmatrix}}}$

Skia de Google solía utilizar la matriz de rango completo de 8 bits mencionada anteriormente, lo que generaba un ligero efecto de reverdecimiento en las imágenes JPEG codificadas por dispositivos Android, más notorio al guardarlas repetidamente. El problema se solucionó en 2016, cuando se utilizó la versión más precisa en su lugar. Debido a las optimizaciones SIMD en libjpeg-turbo , la versión precisa es en realidad más rápida. ^[14]

Los archivos RGB suelen estar codificados en 8, 12, 16 o 24 bits por píxel. En estos ejemplos, asumiremos 24 bits por píxel, que se escribe como RGB888 . El formato de byte estándar es simplemente r0, g0, b0, r1, g1, b1, ....

Los formatos de píxeles empaquetados YCbCr se conocen a menudo como "YUV". Estos archivos se pueden codificar en 12, 16 o 24 bits por píxel. Según el submuestreo, los formatos se pueden describir en gran medida como 4:4:4, 4:2:2 y 4:2:0p. El apóstrofo después de la Y se suele omitir, al igual que la "p" (de planar) después de YUV420p. En términos de formatos de archivo reales, 4:2:0 es el más común, ya que los datos son más reducidos, y la extensión de archivo suele ser ".YUV". La relación entre la velocidad de datos y el muestreo (A:B:C) se define por la relación entre el canal Y y el canal U y V. ^{[15] [16]} La notación de "YUV" seguida de tres números es vaga: los tres números podrían hacer referencia al submuestreo (como se hace en "YUV420"), o podrían hacer referencia a la profundidad de bits en cada canal (como se hace en "YUV565"). La forma inequívoca de referirse a estos formatos es a través del código FourCC . ^[17]

Para convertir de RGB a YUV o viceversa, lo más sencillo es utilizar RGB888 y 4:4:4. Para 4:1:1, 4:2:2 y 4:2:0, primero es necesario convertir los bytes a 4:4:4.

El formato 4:4:4 es sencillo, ya que no se realiza ninguna agrupación de píxeles: la diferencia radica únicamente en la cantidad de bits que se asignan a cada canal y su disposición. El YUV3esquema básico utiliza 3 bytes por píxel, con el orden y0, u0, v0, y1, u1, v1(usando "u" para Cb y "v" para Cr; lo mismo se aplica al contenido que se muestra a continuación). ^[17] En las computadoras, es más común ver un AYUVformato que agrega un canal alfa y pasa a a0, y0, u0, v0, a1, y1, u1, v1, porque los grupos de 32 bits son más fáciles de manejar. ^[15]

4:2:2 agrupa 2 píxeles horizontalmente en cada "contenedor" conceptual. Existen dos disposiciones principales: ^[16]

• YUY2: también llamado YUYV, se ejecuta en el formato y0, u, y1, v.

  

• UYVY: el reverso intercambiado de bytes de YUY2, se ejecuta en el formato u, y0, v, y1.

El formato 4:1:1 se utiliza raramente. Los píxeles se encuentran en grupos horizontales de 4. ^[16]

El formato 4:2:0 es muy utilizado. Los principales formatos son IMC2, IMC4, YV12 y NV12. ^[16] Estos cuatro formatos son "planares", lo que significa que los valores Y, U y V están agrupados en lugar de intercalados. Todos ocupan 12 bits por píxel, suponiendo un canal de 8 bits.

• IMC2 primero presenta las imágenes completas en Y. Luego organiza cada línea de croma en el orden V ₀ ... V _n , U ₀ ... U _n , donde n es el número de muestras de croma por línea, igual a la mitad del ancho de Y.
• IMC4 es similar a IMC2, excepto que se ejecuta en U ₀ ... U _n , V ₀ ... V _n .
• El I420 es un diseño más simple y se usa con más frecuencia. Se escribe la imagen completa en Y, seguida de la imagen en U y, luego, la imagen completa en V.

  

• YV12 sigue el mismo diseño general que I420, solo que se invierte el orden entre las imágenes U y V. ^[18]
• NV12 es posiblemente el formato 4:2:0 de 8 bits más utilizado. Es el valor predeterminado para la vista previa de la cámara de Android . ^[19] Se escribe toda la imagen en Y, seguida de líneas intercaladas que van U ₀ , V ₀ , U ₁ , V ₁ , etc.

También existen variantes "en mosaico" de formatos planares. ^[20]

• Calculadora de Y′CbCr, incluida BT.1886
• Charles Poynton: Preguntas frecuentes sobre el color
• Charles Poynton — Ingeniería de video
• Visualización del espacio de color
• Espacios de color YUV, YCbCr, YPbPr.
• Definición de YCbCr

Recursos de software para píxeles empaquetados:

• Kohn, Mike. Y′UV422 a RGB mediante SSE/Assembly
• libio
• pixfc-sse: biblioteca C de conversiones de formatos de color optimizadas para SSE
• Archivos YUV: archivos de video YUV/RGB de muestra/demostración en muchos formatos YUV, que lo ayudan durante las pruebas.