Frecuencia rotacional

Frecuencia rotacional
La velocidad angular ω (en radianes por segundo), es mayor que la frecuencia de rotación ν (en Hz ), por un factor de 2π.
Otros nombres	velocidad de rotación, tasa de rotación
Símbolos comunes	${\estilo de visualización \nu}$, sust.
Unidad SI	Hz
Otras unidades	rpm , cps
En unidades base del SI	el -1
Derivaciones de otras magnitudes	ν =ω/(2π  rad), n = d N /d t
Dimensión	${\displaystyle {\mathsf {T}}^{-1}}$

Parte de una serie sobre
Mecánica clásica
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$ Segunda ley del movimiento
Historia Cronología Libros de texto
Sucursales Aplicado Celestial Continuo Dinámica Teoría de campos Cinemática Cinética Estática Mecánica estadística
Fundamentos Aceleración Momento angular Pareja Principio de D'Alembert Energía cinético potencial Fuerza Marco de referencia Marco de referencia inercial Impulso Inercia  / Momento de inercia Masa Potencia mecánica Trabajo mecánico Momento Impulso Espacio Velocidad Tiempo Esfuerzo de torsión Velocidad Trabajo virtual
Formulaciones Leyes del movimiento de Newton Mecánica analítica Mecánica lagrangiana Mecánica hamiltoniana Mecánica de Routh Ecuación de Hamilton-Jacobi Ecuación de movimiento de Appell Mecánica de Koopman-von Neumann
Temas centrales Mojadura Desplazamiento Ecuaciones de movimiento Leyes del movimiento de Euler Fuerza ficticia Fricción Oscilador armónico Marco de referencia inercial  / no inercial Mecánica del movimiento de partículas planas Movimiento  ( lineal ) Ley de gravitación universal de Newton Leyes del movimiento de Newton Velocidad relativa Cuerpo rígido dinámica Ecuaciones de Euler Movimiento armónico simple Vibración
Rotación Movimiento circular Marco de referencia giratorio Fuerza centrípeta Fuerza centrífuga reactivo Fuerza de Coriolis Péndulo Velocidad tangencial Frecuencia rotacional Aceleración angular  / desplazamiento  / frecuencia  / velocidad
Científicos Kepler Galileo Huygens Newton Horrocas Halley Maupertuis Daniel Bernoulli Juan Bernoulli Euler de Alembert Claro Lagrange Laplace Pescado Hamilton Jacobi Cauchy Rutina Liouville Apelar Gibbs Hombre de negocios de Neumann
Portal de física  Categoría
en a mi

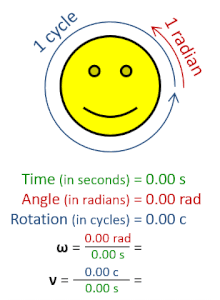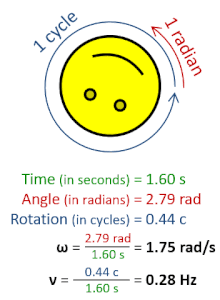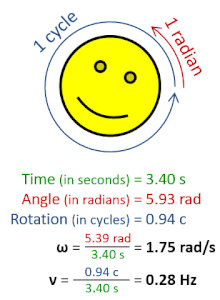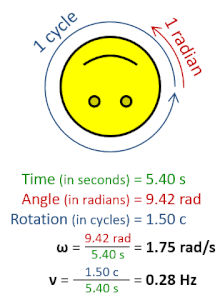
La frecuencia de rotación , también conocida como velocidad de rotación o velocidad de rotación (símbolos ν , nu en minúscula griega y también n ), es la frecuencia de rotación de un objeto alrededor de un eje . Su unidad del SI es el segundo inverso (s ^{−1 ); otras} unidades de medida comunes incluyen el hercio (Hz), los ciclos por segundo (cps) y las revoluciones por minuto (rpm). ^{[1] [a] [b]}

La frecuencia de rotación se puede obtener dividiendo la frecuencia angular , ω, por una vuelta completa (2 π radianes ): ν = ω/(2π  rad). También se puede formular como la tasa instantánea de cambio del número de rotaciones , N , con respecto al tiempo, t : n = d N /d t (según el Sistema Internacional de Cantidades ). ^{[4] Similar al} período ordinario , el recíproco de la frecuencia de rotación es el período de rotación o período de rotación , T = ν ⁻¹ = n ⁻¹ , con dimensión de tiempo (unidad SI segundos ).

La velocidad de rotación es la cantidad vectorial cuya magnitud es igual a la velocidad de rotación escalar . En los casos especiales de giro (alrededor de un eje interno al cuerpo) y revolución (eje externo), la velocidad de rotación puede denominarse velocidad de giro y velocidad de revolución , respectivamente.

La aceleración rotacional es la tasa de cambio de la velocidad rotacional; tiene una dimensión de tiempo recíproco al cuadrado y unidades SI de segundos recíprocos al cuadrado (s ⁻² ); por lo tanto, es una versión normalizada de la aceleración angular y es análoga a la vivacidad .

La velocidad tangencial (letra latina v ), la frecuencia de rotación y la distancia radial están relacionadas por la siguiente ecuación: ^[5]${\displaystyle v}$${\displaystyle \nu }$ ${\displaystyle r}$$${\displaystyle {\begin{aligned}v&=2\pi r\nu \\v&=r\omega .\end{aligned}}}$$

Un reordenamiento algebraico de esta ecuación nos permite resolver la frecuencia rotacional:$${\displaystyle {\begin{aligned}\nu &=v/2\pi r\\\omega &=v/r.\end{aligned}}}$$

Por lo tanto, la velocidad tangencial será directamente proporcional a cuando todas las partes de un sistema tengan simultáneamente la misma , como en el caso de una rueda, un disco o una varilla rígida. La proporcionalidad directa de a no es válida para los planetas , porque estos tienen diferentes frecuencias de rotación.${\displaystyle r}$${\displaystyle \omega }$${\displaystyle v}$${\displaystyle r}$

La frecuencia de rotación puede medir, por ejemplo, la velocidad de funcionamiento de un motor. La velocidad de rotación se utiliza a veces para referirse a la frecuencia angular en lugar de la cantidad definida en este artículo. La frecuencia angular indica el cambio de ángulo por unidad de tiempo, que se expresa con la unidad radianes por segundo en el sistema SI. Dado que 2π radianes o 360 grados corresponden a un ciclo, podemos convertir la frecuencia angular en frecuencia de rotación mediante la siguiente fórmula:$${\displaystyle \nu =\omega /2\pi ,}$$

• ${\displaystyle \nu \,}$es la frecuencia rotacional, con unidades de ciclos por segundo
• ${\displaystyle \omega \,}$es la frecuencia angular, con unidad radianes por segundo o grados por segundo

Por ejemplo, un motor paso a paso puede girar exactamente una revolución completa cada segundo. Su frecuencia angular es de 360 ​​grados por segundo (360°/s), o 2π radianes por segundo (2π rad/s), mientras que la frecuencia de rotación es de 60 rpm.

La frecuencia de rotación no debe confundirse con la velocidad tangencial , a pesar de que existe cierta relación entre ambos conceptos. Imaginemos un tiovivo con una velocidad de rotación constante. No importa lo cerca o lo lejos que estemos del eje de rotación, la frecuencia de rotación permanecerá constante. Sin embargo, la velocidad tangencial no permanece constante. Si nos encontramos a dos metros del eje de rotación, la velocidad tangencial será el doble de la que tendríamos si nos encontráramos a solo un metro del eje de rotación.

• Velocidad angular
• Velocidad radial
• Periodo de rotación
• Espectro rotacional
• Tacómetro