Frecuencia angular

Frecuencia angular
La velocidad angular ω es mayor que la frecuencia de rotación ν por un factor de 2 π .
Otros nombres	velocidad angular, tasa angular
Símbolos comunes	ω
Unidad SI	radián por segundo (rad/s)
Otras unidades	grados por segundo (°/s)
En unidades base del SI	s -1
Derivaciones de otras magnitudes	ω =2 π  rad ⋅  ν , ω =d θ /d t
Dimensión	${\displaystyle {\mathsf {T}}^{-1}}$

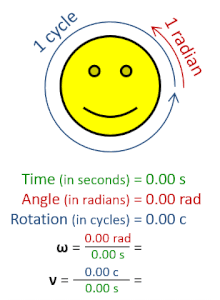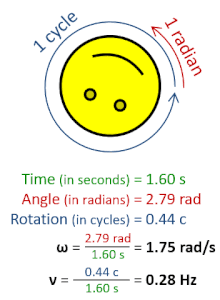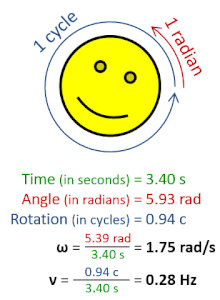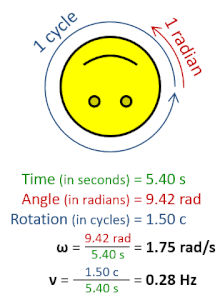
En física , la frecuencia angular (símbolo ω ), también llamada velocidad angular y tasa angular , es una medida escalar de la tasa angular (el ángulo por unidad de tiempo) o la tasa temporal de cambio del argumento de fase de una forma de onda sinusoidal o función seno (por ejemplo, en oscilaciones y ondas). La frecuencia angular (o velocidad angular) es la magnitud de la cantidad pseudovectorial velocidad angular . ^[1]

La frecuencia angular se puede obtener multiplicando la frecuencia de rotación , ν (o frecuencia ordinaria , f ) por una vuelta completa (2 π radianes ): ω = 2 π rad⋅ ν . También se puede formular como ω = d θ /d t , la tasa instantánea de cambio del desplazamiento angular θ , con respecto al tiempo,  t . ^{[2] [3]}

En las unidades del SI , la frecuencia angular normalmente se presenta en la unidad radián por segundo . La unidad hercio (Hz) es dimensionalmente equivalente, pero por convención solo se utiliza para la frecuencia  f , nunca para la frecuencia angular  ω . Esta convención se utiliza para ayudar a evitar la confusión ^[4] que surge cuando se trata de cantidades como la frecuencia y las cantidades angulares porque las unidades de medida (como el ciclo o el radián) se consideran una sola y, por lo tanto, pueden omitirse al expresar cantidades en términos de unidades del SI. ^{[5] [6]}

En el procesamiento de señales digitales , la frecuencia puede normalizarse mediante la frecuencia de muestreo , lo que produce la frecuencia normalizada .

En un objeto que gira o se mueve en órbita, existe una relación entre la distancia al eje, , la velocidad tangencial , , y la frecuencia angular de la rotación. Durante un período, , un cuerpo en movimiento circular recorre una distancia . Esta distancia también es igual a la circunferencia de la trayectoria trazada por el cuerpo, . Igualando estas dos cantidades y recordando la relación entre el período y la frecuencia angular, obtenemos: El movimiento circular en el círculo unitario está dado por donde:${\estilo de visualización r}$${\estilo de visualización v}$${\displaystyle T}$${\displaystyle vT}$${\displaystyle 2\pi r}$${\displaystyle \omega =v/r.}$$${\displaystyle \omega ={\frac {2\pi }{T}}={2\pi f},}$$

• ω es la frecuencia angular (unidad SI: radianes por segundo ),
• T es el período (unidad SI: segundos ),
• f es la frecuencia ordinaria (unidad SI: hercio ).

Part of a series on
Classical mechanics
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$ Second law of motion
History Timeline Textbooks
Branches Applied Celestial Continuum Dynamics Field theory Kinematics Kinetics Statics Statistical mechanics
Fundamentals Acceleration Angular momentum Couple D'Alembert's principle Energy kinetic potential Force Frame of reference Inertial frame of reference Impulse Inertia / Moment of inertia Mass Mechanical power Mechanical work Moment Momentum Space Speed Time Torque Velocity Virtual work
Formulations Newton's laws of motion Analytical mechanics Lagrangian mechanics Hamiltonian mechanics Routhian mechanics Hamilton–Jacobi equation Appell's equation of motion Koopman–von Neumann mechanics
Core topics Damping Displacement Equations of motion Euler's laws of motion Fictitious force Friction Harmonic oscillator Inertial / Non-inertial reference frame Mechanics of planar particle motion Motion (linear) Newton's law of universal gravitation Newton's laws of motion Relative velocity Rigid body dynamics Euler's equations Simple harmonic motion Vibration
Rotation Circular motion Rotating reference frame Centripetal force Centrifugal force reactive Coriolis force Pendulum Tangential speed Rotational frequency Angular acceleration / displacement / frequency / velocity
Scientists Kepler Galileo Huygens Newton Horrocks Halley Maupertuis Daniel Bernoulli Johann Bernoulli Euler d'Alembert Clairaut Lagrange Laplace Poisson Hamilton Jacobi Cauchy Routh Liouville Appell Gibbs Koopman von Neumann
Physics portal  Category
v t e

Un objeto unido a un resorte puede oscilar . Si se supone que el resorte es ideal y sin masa y sin amortiguamiento, entonces el movimiento es simple y armónico con una frecuencia angular dada por ^[7] donde$${\displaystyle \omega ={\sqrt {\frac {k}{m}}},}$$

• k es la constante del resorte ,
• m es la masa del objeto.

ω se denomina frecuencia angular natural (a veces se denota como ω ₀ ).

A medida que el objeto oscila, su aceleración se puede calcular mediante a = − ω 2 x , {\displaystyle a=-\omega ^{2}x,} donde x es el desplazamiento desde una posición de equilibrio.

Usando la frecuencia estándar f , esta ecuación sería$${\displaystyle a=-(2\pi f)^{2}x.}$$

La frecuencia angular resonante en un circuito LC en serie es igual a la raíz cuadrada del recíproco del producto de la capacitancia ( C , con unidad SI faradio ) y la inductancia del circuito ( L , con unidad SI henry ): ^[8]$${\displaystyle \omega ={\sqrt {\frac {1}{LC}}}.}$$

Añadir resistencia en serie (por ejemplo, debido a la resistencia del cable de una bobina) no cambia la frecuencia de resonancia del circuito LC en serie. Para un circuito sintonizado en paralelo, la ecuación anterior suele ser una aproximación útil, pero la frecuencia de resonancia depende de las pérdidas de los elementos en paralelo.

Aunque a menudo se hace referencia a la frecuencia angular vagamente como frecuencia, difiere de la frecuencia en un factor de 2 π , lo que potencialmente genera confusión cuando la distinción no está clara.

• Ciclo por segundo
• Radián por segundo
• Grado (ángulo)
• Movimiento medio
• Frecuencia rotacional
• Movimiento armónico simple

Lectura relacionada:

• Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007). El universo mecánico. Nueva York: Cambridge University Press. pp. 383–385, 391–395. ISBN 978-0-521-71592-8.