Variedad (cibernética)

En cibernética , el término variedad denota el número total de elementos distinguibles de un conjunto , más a menudo el conjunto de estados, entradas o salidas de una máquina de estados finitos o transformación , o el logaritmo binario de la misma cantidad. ^[1] La variedad se utiliza en cibernética como una teoría de la información que se relaciona fácilmente con los autómatas finitos deterministas , y de manera menos formal como una herramienta conceptual para pensar sobre la organización, la regulación y la estabilidad. Es una teoría temprana de la complejidad en autómatas , sistemas complejos , ^{[1] : 6} e investigación de operaciones . ^[2]

El término "variedad" fue introducido por W. Ross Ashby para ampliar su análisis de las máquinas a su conjunto de comportamientos posibles. ^{[3] : 121} Ashby dice: ^{[1] : 126}

La palabra variedad , en relación con un conjunto de elementos distinguibles, se utilizará para significar (i) el número de elementos distintos, o (ii) el logaritmo en base 2 del número, indicando el contexto el sentido utilizado.

En el segundo caso, la variedad se mide en bits . Por ejemplo, una máquina con estados tiene una variedad de cuatro estados o dos bits. La variedad de una secuencia o multiconjunto es el número de símbolos distintos que contiene. Por ejemplo, la secuencia tiene una variedad de cuatro. Como medida de incertidumbre, la variedad está directamente relacionada con la información: . ^{[4] : 26}${\estilo de visualización \{a,b,c,d\}}$${\estilo de visualización a,b,c,c,c,d}$${\displaystyle {\text{Uncertainty}}=-{\text{Information}}}$

Dado que el número de elementos distinguibles depende tanto del observador como del conjunto, "el observador y sus poderes de discriminación pueden tener que especificarse si se quiere definir bien la variedad". ^{[1] : 125} Gordon Pask distinguió entre la variedad del marco de referencia elegido y la variedad del sistema que el observador construye dentro del marco de referencia. El marco de referencia consiste en un espacio de estados y el conjunto de mediciones disponibles para el observador, que tienen una variedad total , donde es el número de estados en el espacio de estados. El sistema que construye el observador comienza con la variedad completa , que se reduce a medida que el observador pierde incertidumbre sobre el estado al aprender a predecir el sistema. Si el observador puede percibir el sistema como una máquina determinista en el marco de referencia dado, la observación puede reducir la variedad a cero a medida que la máquina se vuelve completamente predecible. ^{[4] : 27}${\displaystyle \log _{2}(n)}$${\displaystyle n}$${\displaystyle \log _{2}(n)}$

Las leyes de la naturaleza limitan la variedad de fenómenos al prohibir ciertos comportamientos. ^{[1] : 130} Ashby hizo dos observaciones que consideró leyes de la naturaleza, la ley de la experiencia y la ley de la variedad requerida. La ley de la experiencia sostiene que las máquinas bajo entrada tienden a perder información sobre su estado original, y la ley de la variedad requerida establece una condición necesaria, aunque no suficiente, para que un regulador ejerza un control anticipatorio respondiendo a su entrada actual (en lugar de la salida anterior como en la regulación controlada por errores ).

La ley de la experiencia se refiere a la observación de que la variedad de estados exhibidos por una máquina determinista de forma aislada no puede aumentar, y un conjunto de máquinas idénticas alimentadas con las mismas entradas no puede exhibir una variedad creciente de estados y tiende a sincronizarse en cambio. ^[5]

Es necesario un nombre para este fenómeno. Lo llamaré la ley de la experiencia. Puede describirse de forma más vívida afirmando que la información introducida por el cambio de un parámetro tiende a destruir y reemplazar la información sobre el estado inicial del sistema. ^{[1] : 139}

Esto es una consecuencia de la decadencia de la variedad : una transformación determinista no puede aumentar la variedad de un conjunto. Como resultado, la incertidumbre de un observador sobre el estado de la máquina permanece constante o disminuye con el tiempo. Ashby demuestra que esto también es válido para máquinas con entradas. Bajo cualquier entrada constante, los estados de las máquinas se mueven hacia cualquier atractor que exista en la transformación correspondiente y algunas pueden sincronizarse en estos puntos. Si la entrada cambia a alguna otra entrada y el comportamiento de las máquinas realiza una transformación diferente, más de uno de estos atractores pueden estar en la misma cuenca de atracción bajo . Los estados que llegaron y posiblemente se sincronizaron en esos atractores bajo luego se sincronizan aún más bajo . "En otras palabras", dice Ashby, "los cambios en la entrada de un transductor tienden a hacer que el estado del sistema (en un momento dado) sea menos dependiente del estado inicial individual del transductor y más dependiente de la secuencia particular de valores de parámetros utilizados como entrada". ^{[1] : 136–138}${\displaystyle P_{1}}$${\displaystyle P_{2}}$${\displaystyle P_{2}}$${\displaystyle P_{1}}$${\displaystyle P_{2}}$

Si bien existe una ley de no aumento, solo hay una tendencia a disminuir, ya que la variedad puede mantenerse estable sin disminuir si el conjunto sufre una transformación uno a uno , o si los estados se han sincronizado en un subconjunto para el cual este es el caso. En el análisis del lenguaje formal de máquinas finitas, una secuencia de entrada que sincroniza máquinas idénticas (sin importar la variedad de sus estados iniciales) se denomina palabra sincronizadora .

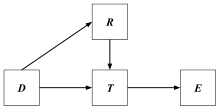
Ashby utilizó la variedad para analizar el problema de la regulación al considerar un juego de dos jugadores , donde un jugador, , proporciona perturbaciones que otro jugador, , debe regular para asegurar resultados aceptables. y cada uno tiene un conjunto de movimientos disponibles, que eligen el resultado de una tabla con tantas filas como movimientos tiene y tantas columnas como movimientos tiene. se le permite el conocimiento completo del movimiento de , y debe elegir movimientos en respuesta para que el resultado sea aceptable. ^{[1] : 202}${\displaystyle D}$${\displaystyle R}$${\displaystyle D}$${\displaystyle R}$${\displaystyle D}$${\displaystyle R}$${\displaystyle R}$${\displaystyle D}$

Como muchos juegos no plantean ninguna dificultad para , la tabla se elige de forma que ningún resultado se repita en ninguna columna, lo que garantiza que en el juego correspondiente cualquier cambio en la jugada de signifique un cambio en el resultado, a menos que tenga una jugada para evitar que el resultado cambie. Con esta restricción, si nunca cambia de jugada, el resultado depende completamente de la elección de , mientras que si tiene múltiples jugadas disponibles puede reducir la variedad de resultados, si la tabla lo permite, dividiendo por tanto como su propia variedad de jugadas. ^{[1] : 204}${\displaystyle R}$${\displaystyle D}$${\displaystyle R}$${\displaystyle R}$${\displaystyle D}$${\displaystyle R}$

${\displaystyle {\begin{array}{c c | c}&&R\\&&{\begin{array}{c c c }\alpha &\beta &\gamma \end{array}}\\\hline D&{\begin{array}{c | c c c }1\\2\\3\\4\\5\\6\end{array}}&{\begin{array}{c c c }\mathbf {a} &f&d\\\mathbf {b} &e&c\\c&d&\mathbf {b} \\d&c&\mathbf {a} \\e&\mathbf {b} &f\\f&\mathbf {a} &e\\\end{array}}\end{array}}}$

La ley de variedad requerida es que una estrategia determinista para puede, en el mejor de los casos, limitar la variedad de resultados a , y solo agregar variedad en los movimientos de puede reducir la variedad de resultados: " solo la variedad puede destruir la variedad ". ^{[1] : 207} Por ejemplo, en la tabla anterior, tiene una estrategia (mostrada en negrita) para reducir la variedad de resultados a , que es en este caso. Ashby consideró que esto era una observación fundamental para la teoría de la regulación.${\displaystyle R}$${\displaystyle {\tfrac {D{\text{'s variety}}}{R{\text{'s variety}}}}}$${\displaystyle R}$${\displaystyle R}$${\displaystyle |\{a,b\}|=2={\tfrac {6}{3}}}$${\displaystyle {\tfrac {D{\text{'s variety}}}{R{\text{'s variety}}}}}$

No es posible reducir más los resultados y seguir respondiendo a todos los movimientos potenciales de , pero es posible que otra mesa con la misma forma no permita hacerlo tan bien. La variedad requerida es necesaria, pero no suficiente para controlar los resultados. Si y son máquinas, no pueden elegir más movimientos que estados. Por lo tanto, un regulador perfecto debe tener al menos tantos estados distinguibles como el fenómeno que se pretende regular (la mesa debe ser cuadrada o más ancha). ${\displaystyle R}$${\displaystyle D}$${\displaystyle R}$${\displaystyle R}$${\displaystyle D}$

Expresada en bits, la ley es . En la teoría de la información de Shannon, , , y son fuentes de información. La condición de que si nunca cambia movimientos, la incertidumbre en los resultados no es menor que la incertidumbre en el movimiento de se expresa como , y dado que la estrategia de es una función determinista del conjunto . Con las reglas del juego expresadas de esta manera, se puede demostrar que . ^{[1] : 207–208} Ashby describió la ley de variedad requerida como relacionada con el décimo teorema en la Teoría matemática de la comunicación de Shannon (1948): ^[6]${\displaystyle V_{O}\geq V_{D}-V_{R}}$${\displaystyle D}$${\displaystyle R}$${\displaystyle E}$${\displaystyle R}$${\displaystyle D}$${\displaystyle H(E|R)\geq H(D|R)}$${\displaystyle R}$${\displaystyle D}$${\displaystyle H(R|D)=0}$${\displaystyle H(E)\geq H(D)-H(R)}$

Esta ley (de la cual el teorema 10 de Shannon relativo a la supresión del ruido es un caso especial) dice que si un regulador impide que una cierta cantidad de perturbación alcance algunas variables esenciales, entonces ese regulador debe ser capaz de ejercer al menos esa cantidad de selección.

Ashby también postuló que la ley de variedad requerida permite la medición de la regulación, es decir, que el requisito para una regulación que funcione bien es que el regulador o los reguladores establecidos estén diseñados para tener en cuenta todos los estados posibles en los que la variable o las variables a regular pueden caer, de modo de garantizar que el resultado esté siempre dentro del rango aceptable. ^{[1] : 209} Ashby vio esta ley como relevante para problemas en biología como la homeostasis y una "riqueza de posibles aplicaciones". Más tarde, en 1970, Conant trabajando con Ashby produjo el teorema del buen regulador ^[7] que requería que los sistemas autónomos adquirieran un modelo interno de su entorno para persistir y lograr la estabilidad (por ejemplo, el criterio de estabilidad de Nyquist ) o el equilibrio dinámico .

Boisot y McKelvey actualizaron esta ley a la "ley de la complejidad requerida" , que sostiene que, para ser eficazmente adaptativo, la complejidad interna de un sistema debe coincidir con la complejidad externa a la que se enfrenta. Otra aplicación práctica de esta ley es la visión de que la alineación de los sistemas de información (SI) es un proceso coevolutivo continuo que reconcilia los "diseños racionales" de arriba hacia abajo y los "procesos emergentes" de abajo hacia arriba de interrelacionar consciente y coherentemente todos los componentes de las relaciones entre el negocio y los SI para contribuir al desempeño de una organización a lo largo del tiempo. ^{[8] [9]}

La aplicación en la gestión de proyectos de la ley de complejidad requerida es el modelo de complejidad positiva, apropiada y negativa propuesto por Stefan Morcov.

Ashby vio inmediatamente las aplicaciones a la organización y la gestión. Una de las implicaciones es que los individuos tienen una capacidad finita para procesar información y, más allá de ese límite, lo que importa es la organización entre individuos. ^[2]

Así, la limitación que se aplica a un equipo de n hombres puede ser mucho mayor, tal vez n veces mayor, que la que se aplica a un hombre individual. Sin embargo, para aprovechar el límite más alto, el equipo debe estar organizado de manera eficiente; y hasta hace poco, nuestro conocimiento de la organización ha sido lamentablemente limitado.

Stafford Beer retomó este análisis en sus escritos sobre cibernética de la gestión . Beer define la variedad como "el número total de estados posibles de un sistema o de un elemento de un sistema". ^[10] Beer reafirma la Ley de la variedad requerida como "La variedad absorbe la variedad". ^[11] Dicho de forma más sencilla, la medida logarítmica de la variedad representa el número mínimo de opciones (por corte binario ) necesarias para resolver la incertidumbre . Beer utilizó esto para asignar los recursos de gestión necesarios para mantener la viabilidad del proceso.

El cibernético Frank George analizó la variedad de equipos que compiten en juegos como el fútbol o el rugby para producir goles o ensayos. Se podría decir que un jugador de ajedrez ganador tiene más variedad que su oponente perdedor. Aquí se implica un orden simple. La atenuación y amplificación de la variedad fueron temas importantes en el trabajo de Stafford Beer en administración ^[10] (la profesión de control, como él la llamaba). La cantidad de personal necesario para responder teléfonos, controlar multitudes o atender a pacientes son ejemplos claros.

La aplicación de señales naturales y analógicas al análisis de variedades requiere una estimación de los "poderes de discriminación" de Ashby (véase la cita anterior). Dado el efecto mariposa de los sistemas dinámicos, se debe tener cuidado antes de poder producir medidas cuantitativas. Pequeñas cantidades, que podrían pasarse por alto, pueden tener grandes efectos. En su obra Designing Freedom, Stafford Beer analiza el caso de un paciente en un hospital con una temperatura que denota fiebre. ^[12] Se deben tomar medidas de inmediato para aislar al paciente. En este caso, ninguna cantidad de variedad que registre la temperatura promedio de los pacientes detectaría esta pequeña señal que podría tener un gran efecto. Se requiere un seguimiento de los individuos, lo que amplifica la variedad (véase las alertas algedónicas en el modelo de sistema viable o VSM). El trabajo de Beer en cibernética de gestión y VSM se basa en gran medida en la ingeniería de variedades.

Otras aplicaciones que involucran la visión de Ashby del conteo de estados incluyen el análisis de los requisitos de ancho de banda digital , redundancia e hinchazón de software , la representación de bits de tipos de datos e índices , conversión de analógico a digital , los límites en máquinas de estados finitos y compresión de datos . Véase también, por ejemplo, Estado excitado , Estado (ciencia informática) , Patrón de estado , Estado (controles) y Autómata celular . La variedad requerida se puede ver en la teoría de la información algorítmica de Chaitin donde un programa más largo y de mayor variedad o una máquina de estados finitos produce una salida incompresible con más variedad o contenido de información.

En general, se establece una descripción de las entradas y salidas requeridas y luego se codifican con la variedad mínima necesaria. La asignación de bits de entrada a bits de salida puede generar una estimación de los componentes mínimos de hardware o software necesarios para producir el comportamiento de control deseado ; por ejemplo, en un programa informático o en un hardware informático .

La variedad es uno de los nueve requisitos que exige un regulador ético . ^[13]

• Cardinalidad
• Complejidad
• Grados de libertad
• Conjunto de potencia
• Practopoyesis
• Teoría de los lechos de agua
• Buen regulador
• Regulador ético
• Estado (Ciencias de la Computación)
• Teorema de Myhill-Nerode
• Complejidad espacial
• Complejidad del proyecto

• Ashby, WR 1956, An Introduction to Cybernetics, Chapman & Hall, 1956, ISBN 0-416-68300-2 (también disponible en formato electrónico como PDF en Principia Cybernetica ) 
• Ashby, WR 1958, Variedad necesaria y sus implicaciones para el control de sistemas complejos, Cybernetica (Namur) Vol. 1, No. 2, 1958.
• Ashby, WR 1960, Diseño para un cerebro; el origen del comportamiento adaptativo, 2ª ed. (Versiones electrónicas en Internet Archive).
• Beer, S. 1974, Designing Freedom, CBC Learning Systems, Toronto, 1974; y John Wiley, Londres y Nueva York, 1975. Traducido al español y al japonés.
• Beer, S. 1975, Platform for Change, John Wiley, Londres y Nueva York. Reimpreso con correcciones en 1978.
• Beer, S. 1979, The Heart of Enterprise, John Wiley, Londres y Nueva York. Reimpreso con correcciones en 1988.
• Beer, S. 1981, Brain of the Firm; Segunda edición (ampliada), John Wiley, Londres y Nueva York. Reimpreso en 1986, 1988. Traducido al ruso.
• Beer, S. 1985, Diagnóstico del sistema para organizaciones; John Wiley, Londres y Nueva York. Traducido al italiano y al japonés. Reimpreso en 1988, 1990, 1991.
• Conant, R. 1981, Mecanismos de inteligencia: artículos y escritos de Ross Ashby, Intersystems Publications, ISBN 1-127-19770-3 . 

Busque variedad en Wikcionario, el diccionario libre.

• La ley de variedad necesaria en los Principia Cybernetica Web , 2001.
• Conceptos de sistemas y el 11 de septiembre Allenna Leonard sobre la variedad necesaria
• Todas las referencias a La Ley de Variedad Requerida en el diario de Ross Ashby 1953-1961.
• Cibernética de gestión: la ley de la variedad necesaria Vídeos introductorios breves de Livas en YouTube
• Practopoiesis: cómo los sistemas biológicos obtienen su variedad
• Conferencias Massey de la CBC de 1973, "Diseñando la libertad"