Marco de referencia inercial

Parte de una serie sobre
Mecánica clásica
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$ Segunda ley del movimiento
Historia Cronología Libros de texto
Sucursales Aplicado Celestial Continuo Dinámica Teoría de campos Cinemática Cinética Estática Mecánica estadística
Fundamentos Aceleración Momento angular Pareja Principio de D'Alembert Energía cinético potencial Fuerza Marco de referencia Marco de referencia inercial Impulso Inercia  / Momento de inercia Masa Potencia mecánica Trabajo mecánico Momento Impulso Espacio Velocidad Tiempo Esfuerzo de torsión Velocidad Trabajo virtual
Formulaciones Leyes del movimiento de Newton Mecánica analítica Mecánica lagrangiana Mecánica hamiltoniana Mecánica de Routh Ecuación de Hamilton-Jacobi Ecuación de movimiento de Appell Mecánica de Koopman-von Neumann
Temas centrales Mojadura Desplazamiento Ecuaciones de movimiento Leyes del movimiento de Euler Fuerza ficticia Fricción Oscilador armónico Marco de referencia inercial/ no inercial Mecánica del movimiento de partículas planas Movimiento  ( lineal ) Ley de gravitación universal de Newton Leyes del movimiento de Newton Velocidad relativa Cuerpo rígido dinámica Ecuaciones de Euler Movimiento armónico simple Vibración
Rotación Movimiento circular Marco de referencia giratorio Fuerza centrípeta Fuerza centrífuga reactivo Fuerza de Coriolis Péndulo Velocidad tangencial Frecuencia rotacional Aceleración angular  / desplazamiento  / frecuencia  / velocidad
Científicos Kepler Galileo Huygens Newton Horrocks Halley Maupertuis Daniel Bernoulli Johann Bernoulli Euler d'Alembert Clairaut Lagrange Laplace Poisson Hamilton Jacobi Cauchy Routh Liouville Appell Gibbs Koopman von Neumann
Physics portal  Category
v t e

En física clásica y relatividad especial , un marco de referencia inercial (también llamado espacio inercial o marco de referencia galileano ) es un marco de referencia estacionario o en movimiento uniforme . Observados en relación con dicho marco, los objetos exhiben inercia , es decir, permanecen en reposo hasta que actúan sobre ellos fuerzas externas, y las leyes de la naturaleza pueden observarse sin necesidad de corrección por aceleración.

Todos los marcos de referencia con aceleración cero se encuentran en un estado de movimiento rectilíneo constante (movimiento en línea recta) entre sí. En un marco de este tipo, se percibe que un objeto sobre el que actúa una fuerza neta cero se mueve con una velocidad constante o, de manera equivalente, se cumple la primera ley del movimiento de Newton . Estos marcos se conocen como inerciales. Algunos físicos, como Isaac Newton , pensaron originalmente que uno de estos marcos era absoluto: el que se aproximaba a las estrellas fijas . Sin embargo, esto no es necesario para la definición y ahora se sabe que esas estrellas, de hecho, se mueven.

Según el principio de la relatividad especial , todas las leyes físicas parecen iguales en todos los sistemas de referencia inerciales, y ningún sistema inercial tiene prioridad sobre otro. Las mediciones de objetos en un sistema inercial se pueden convertir en mediciones en otro mediante una transformación simple: la transformación de Galileo en la física newtoniana o la transformación de Lorentz (combinada con una traslación) en la relatividad especial ; estas coinciden aproximadamente cuando la velocidad relativa de los sistemas es baja, pero difieren a medida que se acerca a la velocidad de la luz .

Por el contrario, un marco de referencia no inercial tiene una aceleración distinta de cero. En un marco de este tipo, las interacciones entre los objetos físicos varían dependiendo de la aceleración de ese marco con respecto a un marco inercial. Visto desde la perspectiva de la mecánica clásica y la relatividad especial , las fuerzas físicas habituales causadas por la interacción de los objetos tienen que ser complementadas por fuerzas ficticias causadas por la inercia . ^{[1] [2]} Visto desde la perspectiva de la teoría de la relatividad general , las fuerzas ficticias (es decir, inerciales) se atribuyen al movimiento geodésico en el espacio-tiempo .

Debido a la rotación de la Tierra , su superficie no es un marco de referencia inercial. El efecto Coriolis puede desviar ciertas formas de movimiento vistas desde la Tierra , y la fuerza centrífuga reducirá la gravedad efectiva en el ecuador . Sin embargo, para muchas aplicaciones, la Tierra es una aproximación adecuada de un marco de referencia inercial.

El movimiento de un cuerpo sólo puede describirse en relación con algo más: otros cuerpos, observadores o un conjunto de coordenadas espacio-temporales. Estos se denominan marcos de referencia . Según el primer postulado de la relatividad especial , todas las leyes físicas toman su forma más simple en un marco inercial, y existen múltiples marcos inerciales interrelacionados por una traslación uniforme :^[3]

Principio especial de relatividad: Si se elige un sistema de coordenadas K de modo que, en relación con él, las leyes físicas se cumplan en su forma más simple, las mismas leyes se cumplen en relación con cualquier otro sistema de coordenadas K' que se mueva en traslación uniforme con respecto a K.

—  Albert Einstein: Los fundamentos de la teoría general de la relatividad , Sección A, §1

Esta simplicidad se manifiesta en que los sistemas inerciales tienen una física autónoma sin necesidad de causas externas, mientras que la física en sistemas no inerciales tiene causas externas. ^[4] El principio de simplicidad se puede utilizar tanto en la física newtoniana como en la relatividad especial: ^{[5] [6]}

Las leyes de la mecánica newtoniana no siempre se cumplen en su forma más simple... Si, por ejemplo, un observador se sitúa sobre un disco que gira con respecto a la Tierra, percibirá una "fuerza" que lo empuja hacia la periferia del disco, que no está causada por ninguna interacción con otros cuerpos. En este caso, la aceleración no es consecuencia de la fuerza habitual, sino de la llamada fuerza inercial. Las leyes de Newton se cumplen en su forma más simple sólo en una familia de sistemas de referencia, llamados sistemas inerciales. Este hecho representa la esencia del principio de relatividad de Galileo:
   las leyes de la mecánica tienen la misma forma en todos los sistemas inerciales.

—  Milutin Blagojević: Gravitación y simetrías de calibre , pag. 4

Sin embargo, se entiende que esta definición de marcos inerciales se aplica al ámbito newtoniano e ignora los efectos relativistas.

En términos prácticos, la equivalencia de los sistemas de referencia inerciales significa que los científicos que se encuentran dentro de una caja que se mueve a una velocidad absoluta constante no pueden determinar esta velocidad mediante ningún experimento. De lo contrario, las diferencias establecerían un sistema de referencia estándar absoluto. ^{[7] [8]} Según esta definición, complementada con la constancia de la velocidad de la luz, los sistemas de referencia inerciales se transforman entre sí según el grupo de transformaciones de simetría de Poincaré, del cual las transformaciones de Lorentz son un subgrupo. ^[9] En la mecánica newtoniana, los sistemas de referencia inerciales están relacionados por el grupo de simetrías de Galileo .

Newton postuló un espacio absoluto que se consideraba bien aproximado por un marco de referencia estacionario con respecto a las estrellas fijas . Un marco inercial era entonces un marco en traslación uniforme con respecto al espacio absoluto. Sin embargo, algunos "relativistas", ^[10] incluso en la época de Newton, pensaban que el espacio absoluto era un defecto de la formulación y que debía ser reemplazado.

La expresión sistema de referencia inercial ( en alemán : Inertialsystem ) fue acuñada por Ludwig Lange en 1885, para reemplazar las definiciones de Newton de "espacio y tiempo absolutos" por una definición más operativa : ^{[11] [12]}

Un marco de referencia en el que un punto de masa lanzado desde el mismo punto en tres direcciones diferentes (no coplanares) sigue trayectorias rectilíneas cada vez que es lanzado, se denomina marco inercial. ^[13]

Blagojevich explica la insuficiencia de la noción de "espacio absoluto" en la mecánica newtoniana: ^[14]

• La existencia del espacio absoluto contradice la lógica interna de la mecánica clásica ya que, según el principio de relatividad galileano, no se puede distinguir ninguno de los sistemas inerciales.
• El espacio absoluto no explica las fuerzas inerciales ya que están relacionadas con la aceleración con respecto a cualquiera de los marcos inerciales.
• El espacio absoluto actúa sobre los objetos físicos induciendo su resistencia a la aceleración, pero no se puede actuar sobre él.

—  Milutin Blagojević: Gravitación y simetrías de calibre , pag. 5

La utilidad de las definiciones operacionales se llevó mucho más lejos en la teoría especial de la relatividad. ^[15] DiSalle proporciona algunos antecedentes históricos, incluida la definición de Lange, y dice en resumen: ^[16]

La pregunta original, "¿con respecto a qué marco de referencia se cumplen las leyes del movimiento?", resulta ser errónea. Las leyes del movimiento determinan esencialmente una clase de marcos de referencia y (en principio) un procedimiento para construirlos.

—  Robert DiSalle Espacio y tiempo: marcos inerciales

Las teorías clásicas que utilizan la transformación de Galileo postulan la equivalencia de todos los sistemas de referencia inerciales. La transformación de Galileo transforma las coordenadas de un sistema de referencia inercial, , a otro, , mediante la simple suma o resta de coordenadas:${\displaystyle \mathbf {s} }$${\displaystyle \mathbf {s} ^{\prime }}$

${\displaystyle \mathbf {r} ^{\prime }=\mathbf {r} -\mathbf {r} _{0}-\mathbf {v} t}$

${\displaystyle t^{\prime }=t-t_{0}}$

donde r ₀ y t ₀ representan desplazamientos en el origen del espacio y el tiempo, y v es la velocidad relativa de los dos sistemas de referencia inerciales. Bajo las transformaciones galileanas, el tiempo t ₂ − t ₁ entre dos eventos es el mismo para todos los sistemas de referencia y la distancia entre dos eventos simultáneos (o, equivalentemente, la longitud de cualquier objeto, | r ₂ − r ₁ |) también es la misma.

Dentro del ámbito de la mecánica newtoniana, un marco de referencia inercial , o marco de referencia inercial, es aquel en el que la primera ley de movimiento de Newton es válida. ^[17] Sin embargo, el principio de relatividad especial generaliza la noción de un marco inercial para incluir todas las leyes físicas, no simplemente la primera ley de Newton.

Newton consideró que la primera ley era válida en cualquier marco de referencia que estuviera en movimiento uniforme (ni rotando ni acelerando) en relación con el espacio absoluto ; como cuestión práctica, se consideró que el "espacio absoluto" eran las estrellas fijas ^{[18] [19]} En la teoría de la relatividad se abandona la noción de espacio absoluto o de marco privilegiado , y un marco inercial en el campo de la mecánica clásica se define como: ^{[20] [21]}

Un marco de referencia inercial es aquel en el que el movimiento de una partícula no sujeta a fuerzas es en línea recta a velocidad constante.

Por lo tanto, con respecto a un sistema inercial, un objeto o cuerpo se acelera solo cuando se le aplica una fuerza física y (siguiendo la primera ley del movimiento de Newton ), en ausencia de una fuerza neta, un cuerpo en reposo permanecerá en reposo y un cuerpo en movimiento continuará moviéndose uniformemente, es decir, en línea recta y a velocidad constante . Los sistemas inerciales newtonianos se transforman entre sí de acuerdo con el grupo de simetrías galileano .

Si se interpreta esta regla como que el movimiento en línea recta es una indicación de fuerza neta cero, la regla no identifica los sistemas de referencia inerciales porque el movimiento en línea recta se puede observar en una variedad de sistemas. Si se interpreta la regla como que define un sistema inercial, entonces es crucial poder determinar cuándo se aplica una fuerza neta cero. Einstein resumió el problema: ^[22]

La debilidad del principio de inercia consiste en que implica un argumento en círculo: una masa se mueve sin aceleración si está suficientemente lejos de otros cuerpos; sabemos que está suficientemente lejos de otros cuerpos sólo por el hecho de que se mueve sin aceleración.

—  Albert Einstein: El significado de la relatividad , pág. 58

Existen varios enfoques para abordar esta cuestión. Un enfoque consiste en argumentar que todas las fuerzas reales disminuyen con la distancia desde sus fuentes de una manera conocida, por lo que solo se necesita que un cuerpo esté lo suficientemente lejos de todas las fuentes para garantizar que no haya ninguna fuerza presente. ^[23] Un posible problema con este enfoque es la visión históricamente duradera de que el universo distante podría afectar a las materias ( principio de Mach ). Otro enfoque consiste en identificar todas las fuentes reales de fuerzas reales y dar cuenta de ellas. Un posible problema con este enfoque es la posibilidad de pasar por alto algo o dar cuenta de manera inapropiada de su influencia, quizás, nuevamente, debido al principio de Mach y a una comprensión incompleta del universo. Un tercer enfoque consiste en observar la forma en que las fuerzas se transforman al cambiar los marcos de referencia. Las fuerzas ficticias, aquellas que surgen debido a la aceleración de un marco, desaparecen en marcos inerciales y tienen reglas complicadas de transformación en casos generales. Con base en la universalidad de la ley física y la solicitud de marcos donde las leyes se expresen de manera más simple, los marcos inerciales se distinguen por la ausencia de tales fuerzas ficticias.

Newton mismo enunció un principio de relatividad en uno de sus corolarios a las leyes del movimiento: ^{[24] [25]}

Los movimientos de los cuerpos incluidos en un espacio dado son los mismos entre sí, ya sea que ese espacio esté en reposo o se mueva uniformemente hacia adelante en línea recta.

—  Isaac Newton: Principia , Corolario V, pág. 88 en la traducción de Andrew Motte

Este principio difiere del principio especial en dos aspectos: primero, está restringido a la mecánica y, segundo, no menciona la simplicidad. Comparte el principio especial de la invariancia de la forma de la descripción entre marcos de referencia que se traducen mutuamente. ^[26] El papel de las fuerzas ficticias en la clasificación de los marcos de referencia se analiza más adelante.

La teoría de la relatividad especial de Einstein , al igual que la mecánica newtoniana, postula la equivalencia de todos los sistemas de referencia inerciales. Sin embargo, como la relatividad especial postula que la velocidad de la luz en el espacio libre es invariante , la transformación entre sistemas inerciales es la transformación de Lorentz , no la transformación galileana que se utiliza en la mecánica newtoniana.

La invariancia de la velocidad de la luz conduce a fenómenos contraintuitivos, como la dilatación del tiempo , la contracción de la longitud y la relatividad de la simultaneidad . Las predicciones de la relatividad especial se han verificado ampliamente experimentalmente. ^[27] La ​​transformación de Lorentz se reduce a la transformación galileana a medida que la velocidad de la luz se acerca al infinito o cuando la velocidad relativa entre fotogramas se acerca a cero. ^[28]

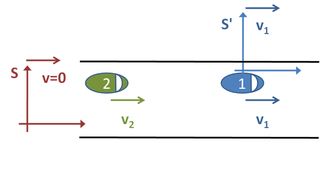
Consideremos una situación común en la vida cotidiana. Dos automóviles viajan por una carretera, ambos a velocidades constantes (véase la Figura 1). En un momento determinado, están separados por 200 metros. El automóvil que va delante viaja a 22 metros por segundo y el que va detrás viaja a 30 metros por segundo. Si queremos averiguar cuánto tiempo tardará el segundo automóvil en alcanzar al primero, hay tres "marcos de referencia" obvios que podríamos elegir. ^[29]

En primer lugar, podríamos observar los dos coches desde el arcén de la carretera. Definimos nuestro "marco de referencia" S de la siguiente manera. Nos situamos al arcén de la carretera y ponemos en marcha un cronómetro en el momento exacto en el que el segundo coche nos pasa, que es cuando están a una distancia d = 200 m de distancia. Como ninguno de los coches está acelerando, podemos determinar sus posiciones mediante las siguientes fórmulas, donde es la posición en metros del coche uno tras el tiempo t en segundos y es la posición del coche dos tras el tiempo t .${\displaystyle x_{1}(t)}$${\displaystyle x_{2}(t)}$

${\displaystyle x_{1}(t)=d+v_{1}t=200+22t,\quad x_{2}(t)=v_{2}t=30t.}$

Observe que estas fórmulas predicen que en t = 0 s el primer automóvil se encuentra a 200 m de distancia y el segundo automóvil está justo a nuestro lado, como se esperaba. Queremos encontrar el tiempo en el que . Por lo tanto, establecemos y resolvemos para , es decir:${\displaystyle x_{1}=x_{2}}$${\displaystyle x_{1}=x_{2}}$${\displaystyle t}$

${\displaystyle 200+22t=30t,}$

${\displaystyle 8t=200,}$

${\displaystyle t=25\ \mathrm {seconds} .}$

Alternativamente, podríamos elegir un sistema de referencia S′ situado en el primer automóvil. En este caso, el primer automóvil está parado y el segundo automóvil se acerca por detrás a una velocidad de v ₂ − v ₁ = 8 m/s . Para alcanzar al primer automóvil, se necesitará un tiempo de ⁠d/v2 - v1_​​⁠ = ⁠200/8⁠ s , es decir, 25 segundos, como antes. Observe cuánto más fácil se vuelve el problema al elegir un marco de referencia adecuado. El tercer marco de referencia posible estaría unido al segundo automóvil. Ese ejemplo se parece al caso que acabamos de analizar, excepto que el segundo automóvil está parado y el primer automóvil se mueve hacia atrás en su dirección a 8 m/s .

Se podría haber elegido un sistema de referencia que girara, acelerara y se moviera de manera complicada, pero esto habría servido para complicar el problema innecesariamente. También es necesario señalar que se pueden convertir las mediciones realizadas en un sistema de coordenadas a otro. Por ejemplo, supongamos que nuestro reloj se adelanta cinco minutos con respecto a la hora estándar local. Si sabemos que es así, cuando alguien nos pregunte qué hora es, podemos restar cinco minutos a la hora que indica nuestro reloj para obtener la hora correcta. Las mediciones que hace un observador sobre un sistema dependen, por tanto, del sistema de referencia del observador (podríamos decir que el autobús llegó a las tres y cinco, cuando en realidad llegó a las tres).

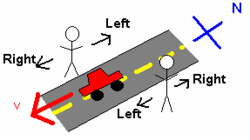
Para dar un ejemplo sencillo que solo implica la orientación de dos observadores, considere a dos personas de pie, una frente a la otra, a ambos lados de una calle que va de norte a sur. Vea la Figura 2. Un automóvil pasa a su lado en dirección sur. Para la persona que mira hacia el este, el automóvil se mueve hacia la derecha. Sin embargo, para la persona que mira hacia el oeste, el automóvil se mueve hacia la izquierda. Esta discrepancia se debe a que las dos personas utilizaron dos marcos de referencia diferentes desde los cuales investigar este sistema.

Para un ejemplo más complejo que involucra observadores en movimiento relativo, considere a Alfred, quien está parado al costado de una carretera mirando un automóvil pasar a su lado de izquierda a derecha. En su marco de referencia, Alfred define el punto donde está parado como el origen, la carretera como el eje x y la dirección frente a él como el eje y positivo . Para él, el automóvil se mueve a lo largo del eje x con cierta velocidad v en la dirección x positiva . El marco de referencia de Alfred se considera un marco inercial porque no está acelerando, ignorando efectos como la rotación de la Tierra y la gravedad.

Ahora, pensemos en Betsy, la persona que conduce el coche. Betsy, al elegir su marco de referencia, define su ubicación como el origen, la dirección a su derecha como el eje x positivo y la dirección frente a ella como el eje y positivo . En este marco de referencia, es Betsy quien está estacionaria y el mundo que la rodea el que se mueve; por ejemplo, cuando pasa junto a Alfred, lo observa moverse con velocidad v en la dirección y negativa . Si está conduciendo hacia el norte, entonces el norte es la dirección y positiva ; si gira hacia el este, el este se convierte en la dirección y positiva .

Por último, como ejemplo de observadores no inerciales, supongamos que Candace está acelerando su coche. Cuando pasa junto a él, Alfred mide su aceleración y descubre que es a en la dirección x negativa . Suponiendo que la aceleración de Candace es constante, ¿qué aceleración mide Betsy? Si la velocidad v de Betsy es constante, está en un marco de referencia inercial y descubrirá que la aceleración es la misma que la de Alfred en su marco de referencia, a en la dirección y negativa . Sin embargo, si está acelerando a una velocidad A en la dirección y negativa (en otras palabras, disminuyendo la velocidad), descubrirá que la aceleración de Candace es a′ = a − A en la dirección y negativa , un valor menor que el que midió Alfred. Del mismo modo, si está acelerando a una velocidad A en la dirección y positiva (aumentando la velocidad), observará que la aceleración de Candace es a′ = a + A en la dirección y negativa , un valor mayor que la medición de Alfred.

En este artículo se analiza la relación entre los marcos de referencia observacionales inerciales y no inerciales. La diferencia básica entre estos marcos es que en los marcos no inerciales se necesitan fuerzas ficticias, como se describe a continuación.

La relatividad general se basa en el principio de equivalencia: ^{[30] [31]}

No hay ningún experimento que los observadores puedan realizar para distinguir si una aceleración surge debido a una fuerza gravitacional o porque su marco de referencia está acelerando.

—  Douglas C. Giancoli, Física para científicos e ingenieros con Física moderna , pág. 155.

Esta idea fue introducida en el artículo de Einstein de 1907 "Principio de relatividad y gravitación" y posteriormente desarrollada en 1911. ^[32] Este principio se apoya en el experimento de Eötvös , que determina si la relación entre la masa inercial y la gravitacional es la misma para todos los cuerpos, independientemente de su tamaño o composición. Hasta la fecha no se ha encontrado ninguna diferencia en unas pocas partes de 10 ¹¹ . ^[33] Para una discusión de las sutilezas del experimento de Eötvös, como la distribución local de la masa alrededor del sitio experimental (incluyendo una broma sobre la masa del propio Eötvös), véase Franklin. ^[34]

La teoría general de Einstein modifica la distinción entre efectos nominalmente "inerciales" y "no inerciales" al reemplazar el espacio de Minkowski "plano" de la relatividad especial por una métrica que produce una curvatura distinta de cero. En la relatividad general, el principio de inercia se reemplaza por el principio de movimiento geodésico , por el cual los objetos se mueven de una manera dictada por la curvatura del espacio-tiempo. Como consecuencia de esta curvatura, no es un hecho en la relatividad general que los objetos inerciales que se mueven a una velocidad particular con respecto a los demás continuarán haciéndolo. Este fenómeno de desviación geodésica significa que los marcos de referencia inerciales no existen globalmente como lo hacen en la mecánica newtoniana y la relatividad especial.

Sin embargo, la teoría general se reduce a la teoría especial sobre regiones suficientemente pequeñas del espacio-tiempo , donde los efectos de la curvatura se vuelven menos importantes y los argumentos anteriores del marco inercial pueden volver a entrar en juego. ^{[35] [36]} En consecuencia, la relatividad especial moderna ahora se describe a veces como solo una "teoría local". ^[37] "Local" puede abarcar, por ejemplo, toda la galaxia de la Vía Láctea : el astrónomo Karl Schwarzschild observó el movimiento de pares de estrellas que orbitan entre sí. Encontró que las dos órbitas de las estrellas de tal sistema se encuentran en un plano, y el perihelio de las órbitas de las dos estrellas permanece apuntando en la misma dirección con respecto al Sistema Solar . Schwarzschild señaló que esto se veía invariablemente: la dirección del momento angular de todos los sistemas estelares dobles observados permanece fija con respecto a la dirección del momento angular del Sistema Solar. Estas observaciones le permitieron concluir que los marcos inerciales dentro de la galaxia no giran entre sí, y que el espacio de la Vía Láctea es aproximadamente galileano o minkowskiano. ^[38]

En un marco inercial, se cumple la primera ley de Newton , la ley de inercia : cualquier movimiento libre tiene una magnitud y dirección constantes. ^[39] La segunda ley de Newton para una partícula toma la forma:

${\displaystyle \mathbf {F} =m\mathbf {a} \ ,}$

donde F es la fuerza neta (un vector ), m la masa de una partícula y a la aceleración de la partícula (también un vector) que sería medida por un observador en reposo en el marco. La fuerza F es la suma vectorial de todas las fuerzas "reales" sobre la partícula, como las fuerzas de contacto , las fuerzas electromagnéticas, gravitacionales y nucleares.

Por el contrario, la segunda ley de Newton en un marco de referencia giratorio (un marco de referencia no inercial ), que gira a una velocidad angular Ω alrededor de un eje, toma la forma:

${\displaystyle \mathbf {F} '=m\mathbf {a} \ ,}$

que parece igual que en un marco inercial, pero ahora la fuerza F ′ es la resultante no solo de F , sino también de términos adicionales (el párrafo que sigue a esta ecuación presenta los puntos principales sin matemáticas detalladas):

${\displaystyle \mathbf {F} '=\mathbf {F} -2m\mathbf {\Omega } \times \mathbf {v} _{B}-m\mathbf {\Omega } \times (\mathbf {\Omega } \times \mathbf {x} _{B})-m{\frac {d\mathbf {\Omega } }{dt}}\times \mathbf {x} _{B}\ ,}$

donde la rotación angular del marco se expresa por el vector Ω que apunta en la dirección del eje de rotación, y con magnitud igual a la velocidad angular de rotación Ω , el símbolo × denota el producto vectorial , el vector x _B ubica el cuerpo y el vector v _B es la velocidad del cuerpo según un observador rotatorio (diferente de la velocidad vista por el observador inercial).

Los términos adicionales en la fuerza F ′ son las fuerzas "ficticias" para este marco, cuyas causas son externas al sistema en el marco. El primer término adicional es la fuerza de Coriolis , el segundo la fuerza centrífuga y el tercero la fuerza de Euler . Todos estos términos tienen estas propiedades: desaparecen cuando Ω = 0; es decir, son cero para un marco inercial (que, por supuesto, no gira); toman una magnitud y dirección diferentes en cada marco giratorio, dependiendo de su valor particular de Ω ; son ubicuos en el marco giratorio (afectan a cada partícula, independientemente de las circunstancias); y no tienen una fuente aparente en fuentes físicas identificables, en particular, la materia . Además, las fuerzas ficticias no disminuyen con la distancia (a diferencia, por ejemplo, de las fuerzas nucleares o eléctricas ). Por ejemplo, la fuerza centrífuga que parece emanar del eje de rotación en un marco giratorio aumenta con la distancia desde el eje.

Todos los observadores coinciden en las fuerzas reales, F ; sólo los observadores no inerciales necesitan fuerzas ficticias. Las leyes de la física en el sistema inercial son más simples porque no hay fuerzas innecesarias.

En la época de Newton, las estrellas fijas se invocaban como marco de referencia, supuestamente en reposo con respecto al espacio absoluto . En los marcos de referencia que estaban en reposo con respecto a las estrellas fijas o en traslación uniforme con respecto a estas estrellas, se suponía que se mantenían las leyes del movimiento de Newton . Por el contrario, en los marcos que se aceleraban con respecto a las estrellas fijas, un caso importante son los marcos que giraban con respecto a las estrellas fijas, las leyes del movimiento no se mantenían en su forma más simple, sino que tenían que ser complementadas con la adición de fuerzas ficticias , por ejemplo, la fuerza de Coriolis y la fuerza centrífuga . Newton ideó dos experimentos para demostrar cómo se podían descubrir estas fuerzas, revelando así a un observador que no estaban en un marco inercial: el ejemplo de la tensión en la cuerda que une dos esferas que giran alrededor de su centro de gravedad, y el ejemplo de la curvatura de la superficie del agua en un cubo giratorio . En ambos casos, la aplicación de la segunda ley de Newton no funcionaría para el observador rotatorio sin invocar las fuerzas centrífugas y de Coriolis para explicar sus observaciones (tensión en el caso de las esferas; superficie parabólica del agua en el caso del cubo giratorio).

Como ya sabemos, las estrellas fijas no lo son. Las que se encuentran en la Vía Láctea giran con la galaxia, exhibiendo movimientos propios . Las que están fuera de nuestra galaxia (como las nebulosas que alguna vez se confundieron con estrellas) también participan en su propio movimiento, en parte debido a la expansión del universo y en parte debido a velocidades peculiares . ^[40] Por ejemplo, la galaxia de Andrómeda está en curso de colisión con la Vía Láctea a una velocidad de 117 km/s. ^[41] El concepto de marcos de referencia inerciales ya no está ligado ni a las estrellas fijas ni al espacio absoluto. Más bien, la identificación de un marco inercial se basa en la simplicidad de las leyes de la física en el marco. Las leyes de la naturaleza toman una forma más simple en los marcos de referencia inerciales porque en estos marcos no era necesario introducir fuerzas inerciales al escribir la ley de movimiento de Newton. ^[42]

En la práctica, el uso de un marco de referencia basado en las estrellas fijas como si fuera un marco de referencia inercial introduce pocas discrepancias. Por ejemplo, la aceleración centrífuga de la Tierra debido a su rotación alrededor del Sol es aproximadamente treinta millones de veces mayor que la del Sol alrededor del centro galáctico. ^[43]

Para ilustrar más, considere la pregunta: "¿El Universo gira?" Una respuesta podría explicar la forma de la galaxia Vía Láctea usando las leyes de la física, ^[44] aunque otras observaciones podrían ser más definitivas; es decir, proporcionar discrepancias más grandes o menos incertidumbre de medición , como la anisotropía de la radiación de fondo de microondas o la nucleosíntesis del Big Bang . ^{[45] [46]} La planitud de la Vía Láctea depende de su tasa de rotación en un marco de referencia inercial. Si su aparente tasa de rotación se atribuye completamente a la rotación en un marco inercial, se predice una "planitud" diferente que si se supone que parte de esta rotación se debe en realidad a la rotación del universo y no debería incluirse en la rotación de la galaxia misma. Basándose en las leyes de la física, se establece un modelo en el que un parámetro es la tasa de rotación del Universo. Si las leyes de la física concuerdan con mayor precisión con las observaciones en un modelo con rotación que sin ella, nos inclinamos a seleccionar el valor de mejor ajuste para la rotación, sujeto a todas las demás observaciones experimentales pertinentes. Si ningún valor del parámetro de rotación es exitoso y la teoría no está dentro del error de observación, se considera una modificación de la ley física, por ejemplo, se invoca la materia oscura para explicar la curva de rotación galáctica . Hasta ahora, las observaciones muestran que cualquier rotación del universo es muy lenta, no más rápida que una vez cada 100 años.6 × 10 ¹³ años (10 ⁻¹³  rad/año), ^[47] y persiste el debate sobre si existe rotación . Sin embargo, si se encontrara rotación, la interpretación de las observaciones en un marco ligado al universo tendría que corregirse para las fuerzas ficticias inherentes a dicha rotación en la física clásica y la relatividad especial, o interpretarse como la curvatura del espacio-tiempo y el movimiento de la materia a lo largo de las geodésicas en la relatividad general. ^[48]

Cuando los efectos cuánticos son importantes, surgen complicaciones conceptuales adicionales en los marcos de referencia cuánticos .

Un marco de referencia acelerado se define a menudo como el marco "preparado", y todas las variables que dependen de ese marco se anotan con primos, por ejemplo, x′ , y′ , a′ .

El vector desde el origen de un marco de referencia inercial hasta el origen de un marco de referencia acelerado se denota comúnmente como R . Dado un punto de interés que existe en ambos marcos, el vector desde el origen inercial hasta el punto se llama r , y el vector desde el origen acelerado hasta el punto se llama r′ .

De la geometría de la situación

${\displaystyle \mathbf {r} =\mathbf {R} +\mathbf {r} '.}$

Tomando la primera y segunda derivada de esto con respecto al tiempo

${\displaystyle \mathbf {v} =\mathbf {V} +\mathbf {v} ',}$

${\displaystyle \mathbf {a} =\mathbf {A} +\mathbf {a} '.}$

donde V y A son la velocidad y la aceleración del sistema acelerado con respecto al sistema inercial y v y a son la velocidad y la aceleración del punto de interés con respecto al marco inercial.

Estas ecuaciones permiten transformaciones entre los dos sistemas de coordenadas; por ejemplo, la segunda ley de Newton se puede escribir como

${\displaystyle \mathbf {F} =m\mathbf {a} =m\mathbf {A} +m\mathbf {a} '.}$

Cuando hay un movimiento acelerado debido a una fuerza ejercida, hay una manifestación de inercia. Si un automóvil eléctrico diseñado para recargar su sistema de batería cuando desacelera cambia a frenado, las baterías se recargan, lo que ilustra la fuerza física de la manifestación de inercia. Sin embargo, la manifestación de inercia no impide la aceleración (o desaceleración), ya que la manifestación de inercia ocurre en respuesta al cambio de velocidad debido a una fuerza. Vista desde la perspectiva de un marco de referencia giratorio, la manifestación de inercia parece ejercer una fuerza (ya sea en dirección centrífuga o en una dirección ortogonal al movimiento de un objeto, el efecto Coriolis ).

Un tipo común de marco de referencia acelerado es un marco que gira y se traslada al mismo tiempo (un ejemplo es un marco de referencia unido a un CD que se reproduce mientras se lleva el reproductor).

Esta disposición conduce a la ecuación (ver Fuerza ficticia para una derivación):

${\displaystyle \mathbf {a} =\mathbf {a} '+{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '+2{\boldsymbol {\omega }}\times \mathbf {v} '+{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')+\mathbf {A} _{0},}$

o, para resolver la aceleración en el marco acelerado,

${\displaystyle \mathbf {a} '=\mathbf {a} -{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '-2{\boldsymbol {\omega }}\times \mathbf {v} '-{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')-\mathbf {A} _{0}.}$

Multiplicando por la masa m se obtiene

${\displaystyle \mathbf {F} '=\mathbf {F} _{\mathrm {physical} }+\mathbf {F} '_{\mathrm {Euler} }+\mathbf {F} '_{\mathrm {Coriolis} }+\mathbf {F} '_{\mathrm {centripetal} }-m\mathbf {A} _{0},}$

dónde

${\displaystyle \mathbf {F} '_{\mathrm {Euler} }=-m{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '}$( Fuerza de Euler ),

${\displaystyle \mathbf {F} '_{\mathrm {Coriolis} }=-2m{\boldsymbol {\omega }}\times \mathbf {v} '}$( Fuerza de Coriolis ),

${\displaystyle \mathbf {F} '_{\mathrm {centrifugal} }=-m{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')=m(\omega ^{2}\mathbf {r} '-({\boldsymbol {\omega }}\cdot \mathbf {r} '){\boldsymbol {\omega }})}$( fuerza centrífuga ).

Los marcos de referencia inerciales y no inerciales se pueden distinguir por la ausencia o presencia de fuerzas ficticias . ^{[1] [2]}

El efecto de este estar en el marco no inercial es requerir que el observador introduzca una fuerza ficticia en sus cálculos…

—  Sidney Borowitz y Lawrence A. Bornstein en Una visión contemporánea de la física elemental , pág. 138

La presencia de fuerzas ficticias indica que las leyes físicas no son las leyes más simples disponibles; en términos del principio especial de relatividad, un marco donde están presentes fuerzas ficticias no es un marco inercial: ^[49]

Las ecuaciones de movimiento en un sistema no inercial difieren de las ecuaciones en un sistema inercial en términos adicionales llamados fuerzas inerciales. Esto nos permite detectar experimentalmente la naturaleza no inercial de un sistema.

—  VI Arnol'd : Métodos matemáticos de la mecánica clásica Segunda edición, pág. 129

Los cuerpos situados en sistemas de referencia no inerciales están sometidos a las llamadas fuerzas ficticias (pseudofuerzas); es decir, fuerzas que resultan de la aceleración del propio sistema de referencia y no de ninguna fuerza física que actúe sobre el cuerpo. Ejemplos de fuerzas ficticias son la fuerza centrífuga y la fuerza de Coriolis en sistemas de referencia giratorios .

Para aplicar la definición newtoniana de un marco inercial, debe quedar clara la separación entre fuerzas "ficticias" y fuerzas "reales".

Por ejemplo, considere un objeto estacionario en un marco inercial. Al estar en reposo, no se aplica ninguna fuerza neta. Pero en un marco que gira alrededor de un eje fijo, el objeto parece moverse en un círculo y está sujeto a la fuerza centrípeta. ¿Cómo se puede decidir que el marco giratorio es un marco no inercial? Hay dos enfoques para esta resolución: un enfoque es buscar el origen de las fuerzas ficticias (la fuerza de Coriolis y la fuerza centrífuga). Se encontrará que no hay fuentes para estas fuerzas, ningún portador de fuerza asociado , ningún cuerpo originario. ^[50] Un segundo enfoque es observar una variedad de marcos de referencia. Para cualquier marco inercial, la fuerza de Coriolis y la fuerza centrífuga desaparecen, por lo que la aplicación del principio de relatividad especial identificaría estos marcos donde las fuerzas desaparecen como compartiendo las mismas y más simples leyes físicas, y por lo tanto dictaminaría que el marco giratorio no es un marco inercial.

Newton examinó este problema por sí mismo utilizando esferas giratorias, como se muestra en la Figura 2 y la Figura 3. Señaló que si las esferas no están girando, la tensión en la cuerda que las ata se mide como cero en cada marco de referencia. ^[51] Si las esferas solo parecen girar (es decir, estamos viendo esferas estacionarias desde un marco giratorio), la tensión cero en la cuerda se explica al observar que la fuerza centrípeta es suministrada por las fuerzas centrífuga y de Coriolis en combinación, por lo que no se necesita tensión. Si las esferas realmente están girando, la tensión observada es exactamente la fuerza centrípeta requerida por el movimiento circular. Por lo tanto, la medición de la tensión en la cuerda identifica el marco inercial: es aquel en el que la tensión en la cuerda proporciona exactamente la fuerza centrípeta demandada por el movimiento tal como se observa en ese marco, y no un valor diferente. Es decir, el marco inercial es aquel en el que las fuerzas ficticias desaparecen.

Para la aceleración lineal , Newton expresó la idea de la indetectabilidad de las aceleraciones en línea recta que se tenían en común: ^[25]

Si los cuerpos, de cualquier manera que se muevan entre sí, son impulsados ​​en la dirección de líneas paralelas por fuerzas de aceleración iguales, continuarán moviéndose entre sí, de la misma manera que si no hubieran sido impulsados ​​por tales fuerzas.

—  Isaac Newton: Principia Corolario VI, pág. 89, en traducción de Andrew Motte

Este principio generaliza la noción de un sistema inercial. Por ejemplo, un observador confinado en un ascensor en caída libre afirmará que él mismo es un sistema inercial válido, incluso si está acelerando bajo la influencia de la gravedad, siempre que no tenga conocimiento de nada que ocurra fuera del ascensor. Por lo tanto, en sentido estricto, el sistema inercial es un concepto relativo. Teniendo esto en cuenta, los sistemas inerciales pueden definirse colectivamente como un conjunto de sistemas que están estacionarios o se mueven a velocidad constante entre sí, de modo que un único sistema inercial se define como un elemento de este conjunto.

Para que estas ideas sean aplicables, todo lo observado en el marco debe estar sujeto a una aceleración base común compartida por el propio marco. Esa situación se aplicaría, por ejemplo, al ejemplo del ascensor, donde todos los objetos están sujetos a la misma aceleración gravitacional y el propio ascensor acelera a la misma velocidad.

Los sistemas de navegación inercial utilizan un conjunto de giroscopios y acelerómetros para determinar las aceleraciones relativas al espacio inercial. Después de que un giroscopio gira en una orientación particular en el espacio inercial, la ley de conservación del momento angular requiere que mantenga esa orientación mientras no se le apliquen fuerzas externas. ^{[52] : 59} Tres giroscopios ortogonales establecen un marco de referencia inercial, y los aceleradores miden la aceleración relativa a ese marco. Las aceleraciones, junto con un reloj, pueden usarse para calcular el cambio de posición. Por lo tanto, la navegación inercial es una forma de navegación por estima que no requiere ninguna entrada externa y, por lo tanto, no puede ser interferida por ninguna fuente de señal externa o interna. ^[53]

Un girocompás , empleado para la navegación de buques marítimos, encuentra el norte geométrico. Lo hace, no detectando el campo magnético de la Tierra, sino utilizando el espacio inercial como referencia. La carcasa exterior del dispositivo girocompás se mantiene de tal manera que permanece alineada con la plomada local. Cuando se hace girar la rueda del giroscopio dentro del dispositivo girocompás, la forma en que está suspendida hace que la rueda del giroscopio alinee gradualmente su eje giratorio con el eje de la Tierra. La alineación con el eje de la Tierra es la única dirección en la que el eje giratorio del giroscopio puede permanecer estacionario con respecto a la Tierra y no se requiere que cambie de dirección con respecto al espacio inercial. Después de girar, un girocompás puede alcanzar la dirección de alineación con el eje de la Tierra en tan solo un cuarto de hora. ^[54]

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (July 2013) (Learn how and when to remove this message)

• Edwin F. Taylor y John Archibald Wheeler , Spacetime Physics , 2.ª edición (Freeman, Nueva York, 1992)
• Albert Einstein , Relatividad, teoría especial y teoría general , 15.ª edición (1954)
• Poincaré, Henri (1900). "La teoría de Lorentz y el príncipe de reacción". Archivos neerlandeses . V : 253–78.
• Albert Einstein , Sobre la electrodinámica de los cuerpos en movimiento , incluido en El principio de relatividad , página 38. Dover 1923

Rotación del Universo

• Julian B. Barbour; Herbert Pfister (1998). Principio de Mach: del cubo de Newton a la gravedad cuántica. Birkhäuser. pág. 445. ISBN 0-8176-3823-7.
• PJ Nahin (1999). Máquinas del tiempo. Saltador. pag. 369; Nota a pie de página 12. ISBN 0-387-98571-9.
• B Ciobanu, I Radinchi Archivado el 19 de julio de 2013 en Wayback Machine Modelado de los campos eléctricos y magnéticos en un universo en rotación Rom. Journ. Phys., Vol. 53, Nos. 1–2, P. 405–415, Bucarest, 2008
• Yuri N. Obukhov, Thoralf Chrobok, Mike Scherfner Archivado el 9 de julio de 2017 en Wayback Machine Inflación rotatoria sin cizallamiento Phys. Rev. D 66, 043518 (2002) [5 páginas]
• Yuri N. Obukhov Sobre los fundamentos físicos y los efectos observacionales de la rotación cósmica (2000)
• Li-Xin Li Archivado el 9 de julio de 2017 en Wayback Machine Efecto de la rotación global del universo en la formación de galaxias Relatividad general y gravitación, 30 (1998) doi :10.1023/A:1018867011142
• P Birch Archivado el 5 de marzo de 2016 en Wayback Machine ¿El universo está girando? Nature 298, 451 – 454 (29 de julio de 1982)
• Kurt Gödel ^{[ enlace muerto permanente ]} Un ejemplo de un nuevo tipo de soluciones cosmológicas de las ecuaciones de campo de gravitación de Einstein Rev. Mod. Phys., Vol. 21, pág. 447, 1949.

• Entrada de la Enciclopedia de Filosofía de Stanford Archivado el 4 de diciembre de 2010 en Wayback Machine
• Clip de animación en YouTube que muestra escenas vistas desde un marco inercial y un marco de referencia giratorio, visualizando las fuerzas de Coriolis y centrífugas.
• "¿La gravedad es una ilusión?". PBS Space Time . 3 de junio de 2015. Archivado desde el original el 13 de noviembre de 2021 – vía YouTube .