Código turbo

En teoría de la información , los códigos turbo (originalmente en francés Turbocodes ) son una clase de códigos de corrección de errores hacia adelante (FEC) de alto rendimiento desarrollados alrededor de 1990-91, pero publicados por primera vez en 1993. Fueron los primeros códigos prácticos en acercarse a la capacidad máxima del canal o límite de Shannon , un máximo teórico para la tasa de código en la que aún es posible una comunicación confiable dado un nivel de ruido específico. Los códigos turbo se utilizan en comunicaciones móviles 3G / 4G (por ejemplo, en UMTS y LTE ) y en comunicaciones satelitales ( de espacio profundo ) , así como otras aplicaciones donde los diseñadores buscan lograr una transferencia de información confiable a través de enlaces de comunicación con restricciones de ancho de banda o latencia en presencia de ruido que corrompe los datos. Los códigos turbo compiten con los códigos de verificación de paridad de baja densidad (LDPC), que brindan un rendimiento similar. Hasta que expiró la patente de los códigos turbo, ^[1] el estado libre de patentes de los códigos LDPC fue un factor importante en la relevancia continua de LDPC. ^[2]

El nombre "código turbo" surgió del bucle de retroalimentación utilizado durante la decodificación normal del código turbo, que se comparó con la retroalimentación de escape utilizada para la turboalimentación del motor . Hagenauer ha argumentado que el término "código turbo" es un nombre inapropiado ya que no hay retroalimentación involucrada en el proceso de codificación. ^[3]

La solicitud de patente fundamental para los códigos turbo se presentó el 23 de abril de 1991. La solicitud de patente menciona a Claude Berrou como el único inventor de los códigos turbo. La solicitud de patente dio lugar a varias patentes, incluida la patente estadounidense 5.446.747, que expiró el 29 de agosto de 2013.

El primer artículo público sobre códigos turbo fue " Codificación y decodificación con corrección de errores en el límite de Shannon cercano: códigos turbo ". ^[4] Este artículo se publicó en 1993 en las Actas de la Conferencia de Comunicaciones Internacionales del IEEE. El artículo de 1993 se formó a partir de tres presentaciones separadas que se combinaron debido a limitaciones de espacio. La fusión hizo que el artículo enumerara a tres autores: Berrou, Glavieux y Thitimajshima (de Télécom Bretagne, ex ENST Bretagne , Francia). Sin embargo, está claro a partir de la presentación de la patente original que Berrou es el único inventor de los códigos turbo y que los otros autores del artículo contribuyeron con material distinto a los conceptos centrales. ^{[ síntesis incorrecta ]}

Los códigos turbo fueron tan revolucionarios en el momento de su introducción que muchos expertos en el campo de la codificación no creyeron en los resultados publicados. Cuando se confirmó el rendimiento, se produjo una pequeña revolución en el mundo de la codificación que condujo a la investigación de muchos otros tipos de procesamiento iterativo de señales. ^[5]

La primera clase de código turbo fue el código convolucional concatenado paralelo (PCCC). Desde la introducción de los códigos turbo paralelos originales en 1993, se han descubierto muchas otras clases de código turbo, incluidos los códigos convolucionales concatenados en serie y los códigos de repetición-acumulación . Los métodos de decodificación turbo iterativos también se han aplicado a sistemas FEC más convencionales, incluidos los códigos convolucionales corregidos de Reed-Solomon, aunque estos sistemas son demasiado complejos para las implementaciones prácticas de decodificadores iterativos. La ecualización turbo también surgió del concepto de codificación turbo.

Además de los códigos turbo, Berrou también inventó los códigos convolucionales sistemáticos recursivos (RSC), que se utilizan en la implementación de ejemplo de los códigos turbo que se describe en la patente. Los códigos turbo que utilizan códigos RSC parecen funcionar mejor que los códigos turbo que no utilizan códigos RSC.

Antes de los códigos turbo, las mejores construcciones eran códigos concatenados en serie basados ​​en un código de corrección de errores Reed-Solomon externo combinado con un código convolucional de longitud de restricción corta decodificado por Viterbi interno , también conocidos como códigos RSV.

En un artículo posterior, Berrou atribuyó el mérito a la intuición de «G. Battail, J. Hagenauer y P. Hoeher, quienes, a finales de los años 80, destacaron el interés del procesamiento probabilístico». Y añadió: « R. Gallager y M. Tanner ya habían imaginado técnicas de codificación y descodificación cuyos principios generales están estrechamente relacionados», aunque los cálculos necesarios eran poco prácticos en ese momento. ^[6]

Existen muchas instancias diferentes de códigos turbo que utilizan diferentes codificadores de componentes, relaciones de entrada/salida, intercaladores y patrones de perforación . Esta implementación de codificador de ejemplo describe un codificador turbo clásico y demuestra el diseño general de códigos turbo paralelos.

Esta implementación del codificador envía tres subbloques de bits. El primer subbloque es el bloque de m bits de datos de carga útil. El segundo subbloque son n/2 bits de paridad para los datos de carga útil, calculados utilizando un código convolucional sistemático recursivo (código RSC). El tercer subbloque son n/2 bits de paridad para una permutación conocida de los datos de carga útil, nuevamente calculados utilizando un código RSC. Por lo tanto, se envían dos subbloques redundantes pero diferentes de bits de paridad con la carga útil. El bloque completo tiene m + n bits de datos con una tasa de código de m /( m + n ) . La permutación de los datos de carga útil se lleva a cabo mediante un dispositivo llamado entrelazador .

En cuanto al hardware, este codificador de código turbo consta de dos codificadores RSC idénticos, C ₁ y C ₂ , como se muestra en la figura, que están conectados entre sí mediante un esquema de concatenación, llamado concatenación paralela :

En la figura, M es un registro de memoria. La línea de retardo y el entrelazador fuerzan a que los bits de entrada d _k aparezcan en secuencias diferentes. En la primera iteración, la secuencia de entrada d _k aparece en ambas salidas del codificador, x _k e y _1k o y _2k debido a la naturaleza sistemática del codificador. Si los codificadores C ₁ y C ₂ se utilizan en n ₁ y n ₂ iteraciones, sus tasas son respectivamente iguales a

${\displaystyle {\begin{aligned}~R_{1}&={\frac {n_{1}+n_{2}}{2n_{1}+n_{2}}}\\~R_{2}&={\frac {n_{1}+n_{2}}{n_{1}+2n_{2}}}\end{aligned}}}$

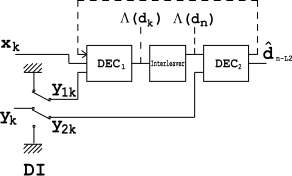
El decodificador está construido de manera similar al codificador anterior. Dos decodificadores elementales están interconectados entre sí, pero en serie, no en paralelo. El decodificador funciona a una velocidad más baja (es decir, ), por lo tanto, está destinado al codificador y es para correspondientemente. produce una decisión suave que causa demora. La misma demora es causada por la línea de demora en el codificador. La operación de causa demora.${\displaystyle \textstyle DIC_ {1}}$${\displaystyle \textstyle R_ {1}}$${\displaystyle \textstyle C_ {1}}$${\displaystyle \textstyle DIC_ {2}}$${\displaystyle \textstyle C_{2}}$${\displaystyle \textstyle DIC_ {1}}$${\displaystyle \textstyle L_ {1}}$${\displaystyle \textstyle DIC_ {2}}$${\displaystyle \textstyle L_ {2}}$

Aquí se utiliza un intercalador instalado entre los dos decodificadores para dispersar las ráfagas de error que llegan desde la salida. El bloque DI es un módulo de demultiplexación e inserción. Funciona como un conmutador, redirigiendo los bits de entrada a en un momento y a en otro. En estado OFF, alimenta las entradas y con bits de relleno (ceros).${\displaystyle \textstyle DIC_ {1}}$${\displaystyle \textstyle DIC_ {1}}$${\displaystyle \textstyle DIC_ {2}}$${\displaystyle \textstyle y_{1k}}$${\displaystyle \textstyle y_{2k}}$

Considere un canal AWGN sin memoria y suponga que en la iteración k , el decodificador recibe un par de variables aleatorias:

${\displaystyle {\begin{aligned}~x_{k}&=(2d_{k}-1)+a_{k}\\~y_{k}&=2(Y_{k}-1)+b_{k}\end{aligned}}}$

donde y son componentes de ruido independientes que tienen la misma varianza . es un k -ésimo bit de la salida del codificador.${\displaystyle \textstyle a_ {k}}$${\displaystyle \textstyle b_ {k}}$${\displaystyle \textstyle \sigma ^{2}}$${\displaystyle \textstyle Y_{k}}$${\displaystyle \textstyle y_{k}}$

La información redundante se demultiplexa y se envía a través de DI a (cuando ) y a (cuando ).${\displaystyle \textstyle DEC_{1}}$${\displaystyle \textstyle y_{k}=y_{1k}}$${\displaystyle \textstyle DEC_{2}}$${\displaystyle \textstyle y_{k}=y_{2k}}$

${\displaystyle \textstyle DEC_{1}}$produce una decisión suave, es decir:

${\displaystyle \Lambda (d_{k})=\log {\frac {p(d_{k}=1)}{p(d_{k}=0)}}}$

y lo entrega a . se llama logaritmo de la razón de verosimilitud (LLR). es la probabilidad a posteriori (APP) del bit de datos que muestra la probabilidad de interpretar un bit recibido como . Si se tiene en cuenta la LLR , se obtiene una decisión difícil; es decir, un bit decodificado.${\displaystyle \textstyle DEC_{2}}$${\displaystyle \textstyle \Lambda (d_{k})}$${\displaystyle \textstyle p(d_{k}=i),\,i\in \{0,1\}}$${\displaystyle \textstyle d_{k}}$${\displaystyle \textstyle d_{k}}$${\displaystyle \textstyle i}$${\displaystyle \textstyle DEC_{2}}$

Se sabe que el algoritmo de Viterbi no puede calcular APP, por lo que no se puede utilizar en . En su lugar, se utiliza un algoritmo BCJR modificado. Para , el algoritmo de Viterbi es adecuado.${\displaystyle \textstyle DEC_{1}}$${\displaystyle \textstyle DEC_{2}}$

Sin embargo, la estructura mostrada no es óptima, ya que utiliza solo una fracción adecuada de la información redundante disponible. Para mejorar la estructura, se utiliza un bucle de retroalimentación (ver la línea de puntos en la figura).${\displaystyle \textstyle DEC_{1}}$

El front-end del decodificador produce un entero para cada bit del flujo de datos. Este entero es una medida de la probabilidad de que el bit sea 0 o 1 y también se denomina bit suave . El entero se puede extraer del rango [−127, 127], donde:

• −127 significa "seguramente 0"
• −100 significa "muy probable 0"
• 0 significa "podría ser 0 o 1"
• 100 significa "muy probable 1"
• 127 significa "seguramente 1"

Esto introduce un aspecto probabilístico al flujo de datos desde el front-end, pero transmite más información sobre cada bit que solo 0 o 1.

Por ejemplo, para cada bit, el extremo frontal de un receptor inalámbrico tradicional tiene que decidir si un voltaje analógico interno está por encima o por debajo de un nivel de voltaje umbral determinado. En el caso de un decodificador de código turbo, el extremo frontal proporcionaría una medida entera de qué tan lejos está el voltaje interno del umbral determinado.

Para decodificar el bloque de datos de m + n bits, el decodificador crea un bloque de medidas de probabilidad, con una medida de probabilidad para cada bit en el flujo de datos. Hay dos decodificadores paralelos, uno para cada uno de los subbloques de paridad de n ⁄ 2 bits. Ambos decodificadores utilizan el subbloque de m probabilidades para los datos de carga útil. El decodificador que trabaja en el segundo subbloque de paridad conoce la permutación que el codificador utilizó para este subbloque.

La innovación clave de los códigos turbo es cómo utilizan los datos de probabilidad para conciliar las diferencias entre los dos decodificadores. Cada uno de los dos decodificadores convolucionales genera una hipótesis (con probabilidades derivadas) para el patrón de m bits en el subbloque de carga útil. Los patrones de bits de hipótesis se comparan y, si difieren, los decodificadores intercambian las probabilidades derivadas que tienen para cada bit en las hipótesis. Cada decodificador incorpora las estimaciones de probabilidad derivadas del otro decodificador para generar una nueva hipótesis para los bits en la carga útil. Luego comparan estas nuevas hipótesis. Este proceso iterativo continúa hasta que los dos decodificadores presentan la misma hipótesis para el patrón de m bits de la carga útil, normalmente en 15 a 18 ciclos.

Se puede establecer una analogía entre este proceso y el de resolver crucigramas o sudokus . Consideremos un crucigrama parcialmente completado, posiblemente confuso. Dos solucionadores de crucigramas (decodificadores) están tratando de resolverlo: uno posee solo las pistas "abajo" (bits de paridad) y el otro posee solo las pistas "a través". Para comenzar, ambos solucionadores adivinan las respuestas (hipótesis) a sus propias pistas, anotando qué tan seguros están de cada letra (bit de carga útil). Luego, comparan notas, intercambiando respuestas y calificaciones de confianza entre sí, notando dónde y cómo difieren. Basándose en este nuevo conocimiento, ambos presentan respuestas y calificaciones de confianza actualizadas, repitiendo todo el proceso hasta que convergen en la misma solución.

Los códigos turbo funcionan bien debido a la atractiva combinación de la aparición aleatoria del código en el canal junto con la estructura de decodificación físicamente realizable. Los códigos turbo se ven afectados por un nivel de error .

Telecomunicaciones:

• Los códigos turbo se utilizan ampliamente en los estándares de telefonía móvil 3G y 4G ; por ejemplo, en HSPA , EV-DO y LTE .
• MediaFLO , sistema de televisión móvil terrestre de Qualcomm .
• El canal de interacción de los sistemas de comunicación por satélite , como DVB-RCS ^[7] y DVB-RCS2.
• Misiones recientes de la NASA, como el Mars Reconnaissance Orbiter, utilizan códigos turbo como alternativa a los códigos decodificadores de Viterbi ( corrección de errores Reed-Solomon) .
• IEEE 802.16 ( WiMAX ), un estándar de red metropolitana inalámbrica, utiliza codificación turbo de bloques y codificación turbo convolucional.

Desde el punto de vista de la inteligencia artificial , los códigos turbo pueden considerarse como un ejemplo de propagación de creencias en bucle en redes bayesianas . ^[8]

• Algoritmo BCJR
• Código convolucional
• Corrección de errores hacia adelante
• Entrelazador
• Código de comprobación de paridad de baja densidad
• Códigos convolucionales concatenados en serie
• Descodificación de decisiones suaves
• Ecualizador turbo
• Algoritmo de Viterbi

• Battail, Gérard (1998). "Un marco conceptual para comprender los códigos turbo". Revista IEEE sobre áreas seleccionadas en comunicaciones . 916 (2): 245–254. doi :10.1109/49.661112.
• Brejza, MF; Li, L.; Maunder, RG; Al-Hashimi, BM; Berrou, C.; Hanzo, L. (2016). "20 años de codificación turbo y pautas de diseño conscientes de la energía para aplicaciones inalámbricas con restricciones energéticas" (PDF) . IEEE Communications Surveys & Tutorials . 918 (1): 8–28. doi :10.1109/COMST.2015.2448692. S2CID  12966388.
• Garzón-Bohórquez, Ronald; Nour, Charbel Abdel; Douillard, Catherine (2016). Mejorando los códigos Turbo para 5G con intercaladores con restricciones de punción de paridad (PDF) . 9º Simposio Internacional sobre Códigos Turbo y Procesamiento Iterativo de Información (ISTC). págs. 151–5. doi :10.1109/ISTC.2016.7593095.

• Guizzo, Erico (marzo de 2004). "Closing In On The Perfect Code". IEEE Spectrum . 41 (3): 36–42. doi :10.1109/MSPEC.2004.1270546. S2CID  21237188. Archivado desde el original el 11 de octubre de 2009.
• "El código turbo UMTS y una implementación de decodificador eficiente adecuada para radios definidas por software" Archivado el 20 de octubre de 2016 en Wayback Machine ( Revista internacional de redes de información inalámbrica )
• Mackenzie, Dana (2005). “Llévalo al límite”. New Scientist . 187 (2507): 38–41.
• "Pushing the Limit", un reportaje de Science News sobre el desarrollo y la génesis de los códigos turbo
• Simposio internacional sobre códigos turbo
• Biblioteca de modulación codificada, una biblioteca de código abierto para simular códigos turbo en Matlab
• "Turbo Equalization: Principles and New Results" Archivado el 27 de febrero de 2009 en Wayback Machine , un artículo de IEEE Transactions on Communications sobre el uso de códigos convolucionales junto con la ecualización de canal.
• Página de inicio de IT++ IT++ es una potente biblioteca de C++ que, en particular, admite códigos turbo.
• Publicaciones de códigos turbo de David MacKay
• Página de inicio de AFF3CT (una caja de herramientas de corrección rápida de errores) para simulaciones de códigos turbo de alta velocidad en software
• Kerouédan, Sylvie; Berrou, Claude (2010). "Código turbo". Scholarpedia . 5 (4). Scholarpedia.org: 6496. Bibcode : 2010SchpJ...5.6496K. doi : 10.4249/scholarpedia.6496 .
• Diseño de referencia 3GPP LTE Turbo.
• Estimación del rendimiento BER del Turbo Code en AWGN Archivado el 1 de febrero de 2019 en Wayback Machine (MatLab).
• Codificación convolucional concatenada paralela: códigos turbo (MatLab Simulink)