Resonancia acústica
La resonancia acústica es un fenómeno en el que un sistema acústico amplifica ondas sonoras cuya frecuencia coincide con una de sus propias frecuencias naturales de vibración (sus frecuencias de resonancia ).
El término "resonancia acústica" se utiliza a veces para limitar la resonancia mecánica al rango de frecuencia de la audición humana, pero como la acústica se define en términos generales en relación con las ondas vibratorias en la materia, [1] la resonancia acústica puede ocurrir en frecuencias fuera del rango de la audición humana.
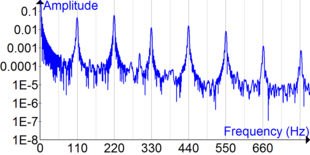
Un objeto acústicamente resonante suele tener más de una frecuencia de resonancia, especialmente en los armónicos de resonancia más fuertes. Vibrará fácilmente en esas frecuencias y vibrará con menos fuerza en otras frecuencias. "Seleccionará" su frecuencia de resonancia de una excitación compleja, como un impulso o una excitación de ruido de banda ancha. En efecto, está filtrando todas las frecuencias que no sean su resonancia.
La resonancia acústica es un factor importante a tener en cuenta para los constructores de instrumentos, ya que la mayoría de los instrumentos acústicos utilizan resonadores , como las cuerdas y el cuerpo de un violín , la longitud del tubo de una flauta y la forma de la membrana de un tambor. La resonancia acústica también es importante para la audición. Por ejemplo, la resonancia de un elemento estructural rígido, llamado membrana basilar dentro de la cóclea del oído interno, permite que las células ciliadas de la membrana detecten el sonido. (En el caso de los mamíferos, la membrana tiene resonancias que se estrechan a lo largo de su longitud, de modo que las frecuencias altas se concentran en un extremo y las bajas en el otro).
Al igual que la resonancia mecánica, la resonancia acústica puede provocar una falla catastrófica del vibrador. El ejemplo clásico de esto es romper una copa de vino con un sonido a la frecuencia de resonancia exacta del vidrio.
Cuerda vibrante
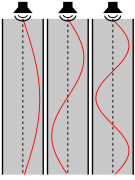
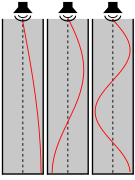
En los instrumentos musicales, las cuerdas bajo tensión, como en los laúdes , arpas , guitarras , pianos , violines , etc., tienen frecuencias de resonancia directamente relacionadas con la masa, la longitud y la tensión de la cuerda. La longitud de onda que creará la primera resonancia en la cuerda es igual al doble de la longitud de la cuerda. Las resonancias más altas corresponden a longitudes de onda que son divisiones enteras de la longitud de onda fundamental . Las frecuencias correspondientes están relacionadas con la velocidad v de una onda que viaja por la cuerda mediante la ecuación
donde L es la longitud de la cuerda (para una cuerda fija en ambos extremos) y n = 1, 2, 3... ( Armónico en un tubo de extremo abierto (es decir, ambos extremos del tubo están abiertos)). La velocidad de una onda a través de una cuerda o alambre está relacionada con su tensión T y la masa por unidad de longitud ρ:
Entonces la frecuencia está relacionada con las propiedades de la cuerda mediante la ecuación
donde T es la tensión , ρ es la masa por unidad de longitud y m es la masa total .
Una tensión más alta y una longitud más corta aumentan las frecuencias de resonancia. Cuando se excita la cuerda con una función impulsiva (un punteo con un dedo o un golpe con un martillo), la cuerda vibra en todas las frecuencias presentes en el impulso (una función impulsiva contiene teóricamente "todas" las frecuencias). Las frecuencias que no forman parte de las resonancias se filtran rápidamente (se atenúan) y todo lo que queda son las vibraciones armónicas que oímos como una nota musical.
Resonancia de cuerdas en instrumentos musicales
La resonancia de cuerdas se produce en los instrumentos de cuerda . Las cuerdas o partes de cuerdas pueden resonar en sus frecuencias fundamentales o armónicas cuando se tocan otras cuerdas. Por ejemplo, una cuerda A a 440 Hz hará que una cuerda E a 330 Hz resuene, porque comparten un armónico de 1320 Hz (el tercer armónico de A y el cuarto armónico de E).
Resonancia de un tubo de aire
La resonancia de un tubo de aire está relacionada con la longitud del tubo, su forma y si tiene extremos cerrados o abiertos. Muchos instrumentos musicales se parecen a los tubos que son cónicos o cilíndricos (ver orificio ). Un tubo que está cerrado en un extremo y abierto en el otro se dice que está tapado o cerrado mientras que un tubo abierto está abierto en ambos extremos. Las flautas orquestales modernas se comportan como tubos cilíndricos abiertos; los clarinetes se comportan como tubos cilíndricos cerrados; y los saxofones , oboes y fagotes como tubos cónicos cerrados, [2] mientras que la mayoría de los instrumentos de lengüeta modernos ( instrumentos de viento metal ) son acústicamente similares a los tubos cónicos cerrados con algunas desviaciones (ver tonos de pedal y tonos falsos ). Al igual que las cuerdas, las columnas de aire vibrantes en tubos cilíndricos o cónicos ideales también tienen resonancias en armónicos, aunque existen algunas diferencias.
Cilindros
Cualquier cilindro resuena en múltiples frecuencias, produciendo múltiples tonos musicales. La frecuencia más baja se denomina frecuencia fundamental o primer armónico. Los cilindros que se utilizan como instrumentos musicales generalmente están abiertos, ya sea por ambos extremos, como una flauta, o por un extremo, como algunos tubos de órgano. Sin embargo, un cilindro cerrado por ambos extremos también se puede utilizar para crear o visualizar ondas sonoras, como en un tubo de Rubens .
Las propiedades de resonancia de un cilindro pueden entenderse considerando el comportamiento de una onda de sonido en el aire. El sonido viaja como una onda de compresión longitudinal, haciendo que las moléculas de aire se muevan de un lado a otro a lo largo de la dirección de viaje. Dentro de un tubo, se forma una onda estacionaria, cuya longitud de onda depende de la longitud del tubo. En el extremo cerrado del tubo, las moléculas de aire no se pueden mover mucho, por lo que este extremo del tubo es un nodo de desplazamiento en la onda estacionaria. En el extremo abierto del tubo, las moléculas de aire pueden moverse libremente, produciendo un antinodo de desplazamiento . Los nodos de desplazamiento son antinodos de presión y viceversa.
Cerrado en ambos extremos
La siguiente tabla muestra las ondas de desplazamiento en un cilindro cerrado en ambos extremos. Nótese que las moléculas de aire cerca de los extremos cerrados no pueden moverse, mientras que las moléculas cerca del centro del tubo se mueven libremente. En el primer armónico, el tubo cerrado contiene exactamente la mitad de una onda estacionaria (nodo- antinodo -nodo). Considerando la onda de presión en esta configuración, los dos extremos cerrados son los antinodos para el cambio en la presión Δ p ; Por lo tanto, en ambos extremos, el cambio en la presión Δ p debe tener la amplitud máxima (o satisfacer ∂(Δp)/∂x = 0 en la forma de la formulación de Sturm–Liouville ), lo que da la ecuación para la onda de presión: . La intuición para esta condición de contorno ∂(Δp)/∂x = 0 en x = 0 y x = L es que la presión de los extremos cerrados seguirá la del punto junto a ellos. Aplicando la condición de contorno ∂(Δp)/∂x = 0 en x = L se obtienen las longitudes de onda de las ondas estacionarias:
Y las frecuencias resonantes son
| Frecuencia | Orden | Nombre 1 | Nombre 2 | Nombre 3 | Representación de ondas | Representación molecular |
|---|---|---|---|---|---|---|
| 1 · f = 440 Hz | n = 1 | 1er parcial | tono fundamental | 1er armónico | 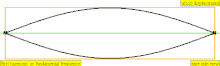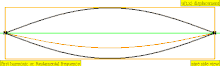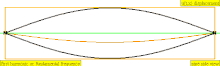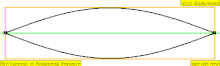 |  |
| 2 · f = 880 Hz | n = 2 | 2do parcial | 1er armónico | 2do armónico |  |  |
| 3·f = 1320 Hz | n = 3 | 3er parcial | 2do armónico | 3er armónico | 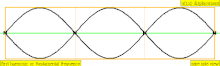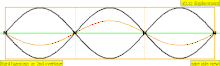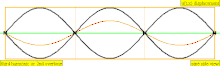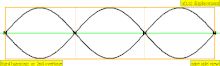 |  |
| 4·f = 1760 Hz | n = 4 | 4to parcial | 3er armónico | 4to armónico | 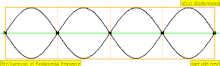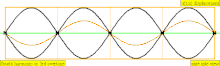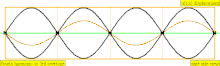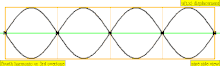 | 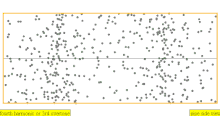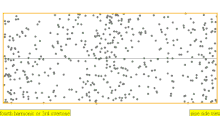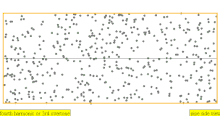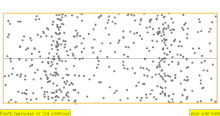 |
Abierto en ambos extremos
En los cilindros con ambos extremos abiertos, las moléculas de aire cercanas al extremo se mueven libremente dentro y fuera del tubo. Este movimiento produce antinodos de desplazamiento en la onda estacionaria. Los nodos tienden a formarse dentro del cilindro, lejos de los extremos. En el primer armónico, el tubo abierto contiene exactamente la mitad de una onda estacionaria (antinodo-nodo-antinodo). Por lo tanto, los armónicos del cilindro abierto se calculan de la misma manera que los armónicos de un cilindro cerrado/cerrado.
La física de una tubería abierta por ambos extremos se explica en el Aula de Física. Observe que los diagramas de esta referencia muestran ondas de desplazamiento, similares a las que se muestran arriba. Estas contrastan marcadamente con las ondas de presión que se muestran cerca del final del presente artículo.
Al soplar con más fuerza un tubo abierto, se puede obtener una nota que está una octava por encima de la frecuencia fundamental o nota del tubo. Por ejemplo, si la nota fundamental de un tubo abierto es C1, entonces al soplar con más fuerza el tubo se obtiene C2, que está una octava por encima de C1. [3]
Los tubos cilíndricos abiertos resuenan en las frecuencias aproximadas:
donde n es un entero positivo (1, 2, 3...) que representa el nodo de resonancia, L es la longitud del tubo y v es la velocidad del sonido en el aire (que es de aproximadamente 343 metros por segundo [770 mph] a 20 °C [68 °F]). Esta ecuación proviene de las condiciones de contorno para la onda de presión, que trata los extremos abiertos como nodos de presión donde el cambio de presión Δ p debe ser cero.
A continuación se presenta una ecuación más precisa considerando una corrección final :
donde r es el radio del tubo de resonancia. Esta ecuación compensa el hecho de que el punto exacto en el que una onda sonora se refleja en un extremo abierto no está exactamente en la sección final del tubo, sino a una pequeña distancia fuera del tubo.
La relación de reflexión es ligeramente inferior a 1; el extremo abierto no se comporta como una impedancia acústica infinitesimal ; más bien, tiene un valor finito, llamado impedancia de radiación, que depende del diámetro del tubo, la longitud de onda y el tipo de placa de reflexión posiblemente presente alrededor de la abertura del tubo.
Entonces cuando n es 1:
donde v es la velocidad del sonido, L es la longitud del tubo resonante, r es el radio del tubo, f es la frecuencia del sonido resonante y λ es la longitud de onda resonante.
Cerrado en un extremo
Cuando se utiliza en un órgano, un tubo cerrado en un extremo se denomina "tubo tapado". Estos cilindros tienen una frecuencia fundamental, pero se pueden sobredimensionar para producir otras frecuencias o notas más altas. Estos registros sobredimensionados se pueden afinar utilizando diferentes grados de conicidad. Un tubo cerrado resuena a la misma frecuencia fundamental que un tubo abierto del doble de su longitud, con una longitud de onda igual a cuatro veces su longitud. En un tubo cerrado, siempre aparece un nodo de desplazamiento , o punto sin vibración, en el extremo cerrado y, si el tubo está resonando, tendrá un antinodo de desplazamiento , o punto de mayor vibración en el punto Phi (longitud × 0,618) cerca del extremo abierto.
Al soplar en exceso un tubo cilíndrico cerrado, se puede obtener una nota que está aproximadamente un doceavo por encima de la nota fundamental del tubo, o un quinto por encima de la octava de la nota fundamental. Por ejemplo, si la nota fundamental de un tubo cerrado es C1, entonces soplar en exceso el tubo da G2, que está un doceavo por encima de C1. Alternativamente, podemos decir que G2 está un quinto por encima de C2, la octava por encima de C1. Ajustar la conicidad de este cilindro para un cono decreciente puede afinar el segundo armónico o la nota soplada en exceso cerca de la posición de octava u octava. [4] Abrir un pequeño "agujero de altavoz" en el punto Phi , o posición compartida de "onda/nodo", cancelará la frecuencia fundamental y obligará al tubo a resonar en un doceavo por encima de la fundamental. Esta técnica se utiliza en una flauta dulce al abrir el orificio dorsal del pulgar. Si se mueve este pequeño orificio hacia arriba, más cerca de la entonación, se convertirá en un "orificio de eco" (modificación de la flauta dulce Dolmetsch) que, al abrirlo, emitirá una nota blanca precisa por encima de la fundamental. Nota: Es necesario ajustar ligeramente el tamaño o el diámetro para centrarse en la frecuencia precisa de la nota blanca. [3]
Un tubo cerrado tendrá resonancias aproximadas de:
donde "n" aquí es un número impar (1, 3, 5...). Este tipo de tubo produce solo armónicos impares y tiene su frecuencia fundamental una octava más baja que la de un cilindro abierto (es decir, la mitad de la frecuencia). Esta ecuación proviene de las condiciones de contorno para la onda de presión, que trata el extremo cerrado como antinodos de presión donde el cambio en la presión Δ p debe tener la amplitud máxima, o satisfacer ∂(Δp)/∂x = 0 en la forma de la formulación de Sturm–Liouville . La intuición para esta condición de contorno ∂(Δp)/∂x = 0 en x = L es que la presión del extremo cerrado seguirá la del punto contiguo a él.
A continuación se presenta una ecuación más precisa considerando una corrección final :
- .
Nuevamente, cuando n es 1:
donde v es la velocidad del sonido, L es la longitud del tubo resonante, d es el diámetro del tubo, f es la frecuencia del sonido resonante y λ es la longitud de onda resonante.
Onda de presión
En los dos diagramas siguientes se muestran las tres primeras resonancias de la onda de presión en un tubo cilíndrico, con antinodos en el extremo cerrado del tubo. En el diagrama 1, el tubo está abierto en ambos extremos. En el diagrama 2, está cerrado en un extremo. El eje horizontal es la presión. Nótese que en este caso, el extremo abierto del tubo es un nodo de presión mientras que el extremo cerrado es un antinodo de presión.
- 1
- 2
Conos
Un tubo cónico abierto, es decir, uno en forma de cono truncado con ambos extremos abiertos, tendrá frecuencias de resonancia aproximadamente iguales a las de un tubo cilíndrico abierto de la misma longitud.
Las frecuencias de resonancia de un tubo cónico tapado (un cono o tronco de cono completo con un extremo cerrado) satisfacen una condición más complicada:
donde el número de onda k es
y x es la distancia desde el extremo pequeño del tronco hasta el vértice. Cuando x es pequeño, es decir, cuando el cono está casi completo, esto se convierte en
lo que da lugar a frecuencias de resonancia aproximadamente iguales a las de un cilindro abierto cuya longitud es igual a L + x . En palabras, un tubo cónico completo se comporta aproximadamente como un tubo cilíndrico abierto de la misma longitud y, en primer orden, el comportamiento no cambia si el cono completo se reemplaza por un tronco de cono cerrado.
Caja rectangular cerrada
Las ondas sonoras en una caja rectangular incluyen, por ejemplo, cajas de altavoces y edificios. Los edificios rectangulares tienen resonancias descritas como modos de sala . Para una caja rectangular, las frecuencias de resonancia se dan por [5]
donde v es la velocidad del sonido, L x , L y y L z son las dimensiones de la caja. , , y son números enteros no negativos que no pueden ser todos cero. Si la pequeña caja del altavoz es hermética, la frecuencia es lo suficientemente baja y la compresión es lo suficientemente alta, la presión sonora (nivel de decibeles) dentro de la caja será la misma en cualquier parte dentro de la caja, esto es presión hidráulica.
Resonancia de una esfera de aire (ventilada)
La frecuencia de resonancia de una cavidad rígida de volumen estático V 0 con un orificio de sonido con cuello de área A y longitud L está dada por la fórmula de resonancia de Helmholtz [6] [7]
¿Dónde está la longitud equivalente del cuello con corrección final?
- para un mástil sin brida [8]
- para un cuello con brida
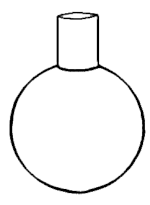
Para una cavidad esférica, la fórmula de frecuencia resonante se convierte en
dónde
- D = diámetro de la esfera
- d = diámetro del orificio de sonido
Para una esfera con solo un orificio de sonido, L = 0 y la superficie de la esfera actúa como una brida, por lo que
En aire seco a 20 °C, con d y D en metros, f en hercios , esto se convierte en
Rotura de vidrio con sonido por resonancia

Esta es una demostración clásica de resonancia. Un vaso tiene una resonancia natural, una frecuencia a la que vibrará fácilmente. Por lo tanto, el vaso necesita ser movido por la onda sonora a esa frecuencia. Si la fuerza de la onda sonora que hace vibrar el vaso es lo suficientemente grande, el tamaño de la vibración será tan grande que el vaso se fracturará. Para hacer esto de manera confiable para una demostración científica se requiere práctica y una elección cuidadosa del vaso y del altavoz. [9]
En la composición musical
Varios compositores han comenzado a hacer de la resonancia el tema de sus composiciones. Alvin Lucier ha utilizado instrumentos acústicos y generadores de ondas sinusoidales para explorar la resonancia de objetos grandes y pequeños en muchas de sus composiciones. Los complejos parciales inarmónicos de un crescendo y decrescendo en forma de oleaje en un tamtam u otro instrumento de percusión interactúan con las resonancias de la sala en Koan: Having Never Written A Note For Percussion de James Tenney . Pauline Oliveros y Stuart Dempster actúan regularmente en grandes espacios reverberantes como la cisterna de 2 millones de galones estadounidenses (7600 m 3 ) en Fort Worden, Washington, que tiene una reverberación con un decaimiento de 45 segundos. " Terpsichord , una pieza para percusión y sonidos pregrabados, [utiliza] las resonancias de los instrumentos acústicos [para] formar puentes sonoros con los sonidos electrónicos pregrabados, que, a su vez, prolongan las resonancias, transformándolas en nuevos gestos sonoros", del profesor de composición y compositor de la Academia de Música de Malmö Kent Olofsson. [ 10]
Véase también
- Armonía
- Teoría musical
- Resonancia
- Reverberación
- Onda estacionaria
- Cuerda simpática
- Cambio de fase de reflexión
Referencias
- ^ Kinsler LE, Frey AR, Coppens AB, Sanders JV, "Fundamentos de acústica", 3.ª edición, ISBN 978-0-471-02933-5 , Wiley, Nueva York, 1982.
- ^ Wolfe, Joe. "Acústica del saxofón: una introducción". Universidad de Nueva Gales del Sur . Consultado el 1 de enero de 2015 .
- ^ ab Kool, Jaap. Das Saxophon . JJ Weber, Leipzig. 1931. Traducido por Lawrence Gwozdz en 1987, analiza los tubos "abiertos" y "cerrados".
- ^ Trompas, cuerdas y armonía , de Arthur H. Benade
- ^ Kuttruff, Heinrich (2007). Acústica: una introducción. Taylor & Francis. pág. 170. ISBN 978-0-203-97089-8.
- ^ Wolfe, Joe. "Resonancia de Helmholtz". Universidad de Nueva Gales del Sur . Consultado el 1 de enero de 2015 .
- ^ Greene, Chad A.; Argo IV, Theodore F.; Wilson, Preston S. (2009). Un experimento con resonador de Helmholtz para el proyecto Listen Up . Actas de reuniones sobre acústica. ASA. p. 025001. doi : 10.1121/1.3112687 .
- ^ Raichel, Daniel R. (2006). La ciencia y las aplicaciones de la acústica . Springer. Págs. 145-149. ISBN. 978-0387-26062-4.
- ^ Centro de investigación acústica (14 de enero de 2019). «Cómo romper un vaso con el sonido». Universidad de Salford . Consultado el 17 de enero de 2019 .
- ^ Olofsson, Kent (4 de febrero de 2015). "Resonancias y respuestas". Divergence Press (4). University of Haddersfield Press. doi :10.5920/divp.2015.48.
- Nederveen, Cornelis Johannes, Aspectos acústicos de los instrumentos de viento de madera . Ámsterdam, Frits Knuf, 1969.
- Rossing, Thomas D., y Fletcher, Neville H., Principios de vibración y sonido . Nueva York, Springer-Verlag, 1995.
Enlaces externos
- Subprograma de ondas estacionarias