La construcción de Thompson
En informática , el algoritmo de construcción de Thompson , también llamado algoritmo McNaughton–Yamada–Thompson , [1] es un método para transformar una expresión regular en un autómata finito no determinista (AFN) equivalente. [2] Este AFN se puede utilizar para hacer coincidir cadenas con la expresión regular. Este algoritmo se le atribuye a Ken Thompson .
Las expresiones regulares y los autómatas finitos no deterministas son dos representaciones de lenguajes formales . Por ejemplo, las utilidades de procesamiento de texto utilizan expresiones regulares para describir patrones de búsqueda avanzados, pero los NFA son más adecuados para su ejecución en una computadora. Por lo tanto, este algoritmo tiene interés práctico, ya que puede compilar expresiones regulares en NFA. Desde un punto de vista teórico, este algoritmo es parte de la prueba de que ambos aceptan exactamente los mismos lenguajes, es decir, los lenguajes regulares .
Un NFA puede volverse determinista mediante la construcción de un conjunto de potencias y luego minimizarse para obtener un autómata óptimo correspondiente a la expresión regular dada. Sin embargo, un NFA también puede interpretarse directamente .
Para decidir si dos expresiones regulares dadas describen el mismo lenguaje, cada una puede convertirse en un autómata finito determinista mínimo equivalente mediante la construcción de Thompson, la construcción de conjuntos potencia y la minimización de DFA . Si, y solo si, los autómatas resultantes concuerdan hasta el cambio de nombre de los estados, los lenguajes de las expresiones regulares concuerdan.
El algoritmo
El algoritmo funciona recursivamente dividiendo una expresión en sus subexpresiones constituyentes, a partir de las cuales se construirá el NFA utilizando un conjunto de reglas. [3] Más precisamente, a partir de una expresión regular E , el autómata obtenido A con la función de transición Δ [ aclaración necesaria ] respeta las siguientes propiedades:
- A tiene exactamente un estado inicial q 0 , al que no se puede acceder desde ningún otro estado. Es decir, para cualquier estado q y cualquier letra a , no contiene q 0 .
- A tiene exactamente un estado final q f , que no es coaccesible desde ningún otro estado. Es decir, para cualquier letra a , .
- Sea c el número de concatenación de la expresión regular E y sea s el número de símbolos aparte de los paréntesis, es decir, | , * , a y ε . Entonces, el número de estados de A es 2 s − c (lineal en el tamaño de E ).
- El número de transiciones para salir de cualquier estado es como máximo dos.
- Dado que un NFA de m estados y como máximo e transiciones desde cada estado puede coincidir con una cadena de longitud n en el tiempo O ( emn ) , un NFA de Thompson puede hacer una coincidencia de patrones en tiempo lineal, asumiendo un alfabeto de tamaño fijo. [4] [ se necesita una mejor fuente ]
Normas
Las siguientes reglas se representan de acuerdo con Aho et al. (2007), [1] p. 122. En lo que sigue, N ( s ) y N ( t ) son los NFA de las subexpresiones s y t , respectivamente.
La expresión vacía ε se convierte en
Un símbolo a del alfabeto de entrada se convierte a
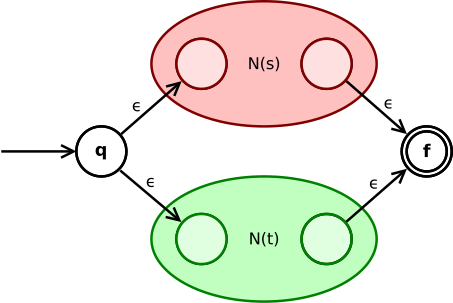
La expresión de unión s | t se convierte en
El estado q pasa a través de ε al estado inicial de N ( s ) o N ( t ). Sus estados finales se convierten en estados intermedios de todo el NFA y se fusionan a través de dos transiciones ε en el estado final del NFA.
La expresión de concatenación st se convierte en
El estado inicial de N ( s ) es el estado inicial de todo el NFA. El estado final de N ( s ) se convierte en el estado inicial de N ( t ). El estado final de N ( t ) es el estado final de todo el NFA.
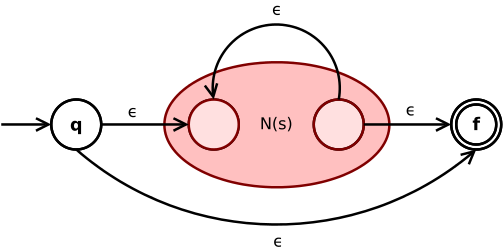
La expresión de estrella de Kleene s * se convierte en
Una ε-transición conecta el estado inicial y final del NFA con el sub-NFA N ( s ) intermedio. Otra ε-transición del estado final interno al estado inicial interno de N ( s ) permite la repetición de la expresión s según el operador estrella.
- La expresión entre paréntesis ( s ) se convierte en N ( s ).
Con estas reglas, utilizando las reglas de expresión vacía y de símbolos como casos base, es posible demostrar con inducción estructural que cualquier expresión regular puede convertirse en un NFA equivalente. [1]
Ejemplo
A continuación se dan dos ejemplos: uno pequeño e informal con el resultado y otro más grande con una aplicación paso a paso del algoritmo.
Pequeño ejemplo

(ε|a*b)utilización de la construcción de Thompson, paso a pasoLa siguiente imagen muestra el resultado de la construcción de Thompson sobre (ε|a*b). El óvalo violeta corresponde a a , el óvalo verde azulado corresponde a a* , el óvalo verde corresponde a b , el óvalo naranja corresponde a a*b y el óvalo azul corresponde a ε .
Aplicación del algoritmo

(0|(1(01*(00)*0)*1)*)*A modo de ejemplo, la imagen muestra el resultado del algoritmo de construcción de Thompson sobre la expresión regular (0|(1(01*(00)*0)*1)*)*que denota el conjunto de números binarios que son múltiplos de 3:
- { ε, "0", "00", "11", "000", "011", "110", "0000", "0011", "0110", "1001", "1100", "1111" , "00000", ... }.
La parte superior derecha muestra la estructura lógica (árbol sintáctico) de la expresión, donde "." denota concatenación (se supone que tiene aridad variable); las subexpresiones se denominan a - q a modo de referencia. La parte izquierda muestra el autómata finito no determinista resultante del algoritmo de Thompson, con el estado de entrada y salida de cada subexpresión coloreado en magenta y cian , respectivamente. Se omite una ε como etiqueta de transición para mayor claridad: las transiciones sin etiqueta son, de hecho, transiciones ε. El estado de entrada y salida correspondiente a la expresión raíz q es el estado de inicio y aceptación del autómata, respectivamente.
Los pasos del algoritmo son los siguientes:
| q : | Comience a convertir la expresión de la estrella de Kleene | (0|(1(01*(00)*0)*1)*)* | ||||||||
| b : | Iniciar la conversión de la expresión de unión | 0|(1(01*(00)*0)*1)* | ||||||||
| a : | convertir símbolo | 0 | ||||||||
| pag : | Comience a convertir la expresión de la estrella de Kleene | (1(01*(00)*0)*1)* | ||||||||
| d : | Iniciar la conversión de la expresión de concatenación | 1(01*(00)*0)*1 | ||||||||
| c : | convertir símbolo | 1 | ||||||||
| uno : | Comience a convertir la expresión de la estrella de Kleene | (01*(00)*0)* | ||||||||
| y : | Iniciar la conversión de la expresión de concatenación | 01*(00)*0 | ||||||||
| mi : | convertir símbolo | 0 | ||||||||
| yo : | Comience a convertir la expresión de la estrella de Kleene | 1* | ||||||||
| g : | convertir símbolo | 1 | ||||||||
| yo : | Terminé de convertir la expresión de estrella de Kleene | 1* | ||||||||
| yo : | Comience a convertir la expresión de la estrella de Kleene | (00)* | ||||||||
| yo : | Iniciar la conversión de la expresión de concatenación | 00 | ||||||||
| i : | convertir símbolo | 0 | ||||||||
| al : | convertir símbolo | 0 | ||||||||
| yo : | Terminé de convertir la expresión de concatenación | 00 | ||||||||
| yo : | Terminé de convertir la expresión de estrella de Kleene | (00)* | ||||||||
| yo : | convertir símbolo | 0 | ||||||||
| y : | Terminé de convertir la expresión de concatenación | 01*(00)*0 | ||||||||
| uno : | Terminé de convertir la expresión de estrella de Kleene | (01*(00)*0)* | ||||||||
| o : | convertir símbolo | 1 | ||||||||
| d : | Terminé de convertir la expresión de concatenación | 1(01*(00)*0)*1 | ||||||||
| pag : | Terminé de convertir la expresión de estrella de Kleene | (1(01*(00)*0)*1)* | ||||||||
| b : | Se terminó de convertir la expresión de unión | 0|(1(01*(00)*0)*1)* | ||||||||
| q : | Terminé de convertir la expresión de estrella de Kleene | (0|(1(01*(00)*0)*1)*)* | ||||||||
A continuación se muestra un autómata determinista mínimo equivalente.

Relación con otros algoritmos
El de Thompson es uno de varios algoritmos para construir NFA a partir de expresiones regulares; [5] un algoritmo anterior fue proporcionado por McNaughton y Yamada. [6] A la inversa de la construcción de Thompson, el algoritmo de Kleene transforma un autómata finito en una expresión regular.
El algoritmo de construcción de Glushkov es similar a la construcción de Thompson, una vez que se eliminan las transiciones ε.
Referencias
- ^ abc Alfred Vaino Aho ; Monica S. Lam ; Ravi Sethi ; Jeffrey D. Ullman (2007). "3.7.4 Construcción de un NFA a partir de una expresión regular" (versión impresa) . Compilers: Principles, Techniques, & Tools (2.ª ed.). Boston, MA, EE. UU.: Pearson Addison-Wesley. pág. 159–163. ISBN 9780321486813.
- ^ Louden, Kenneth C. (1997). "2.4.1 De una expresión regular a un NFA" (versión impresa) . Construcción de compiladores: principios y práctica (3.ª ed.). 20 Park Plaza Boston, MA 02116-4324, EE. UU.: PWS Publishing Company. págs. 64–69. ISBN 978-0-534-93972-4.
{{cite book}}: Mantenimiento de CS1: ubicación ( enlace ) - ^ Ken Thompson (junio de 1968). "Técnicas de programación: algoritmo de búsqueda de expresiones regulares". Comunicaciones de la ACM . 11 (6): 419–422. doi : 10.1145/363347.363387 . S2CID 21260384.
- ^ Xing, Guangming. "NFA de Thompson minimizado" (PDF) .
- ^ Watson, Bruce W. (1995). Una taxonomía de algoritmos de construcción de autómatas finitos (PDF) (Informe técnico). Universidad Tecnológica de Eindhoven . Computing Science Report 93/43.
- ^ R. McNaughton, H. Yamada (marzo de 1960). "Expresiones regulares y gráficos de estados para autómatas". IEEE Transactions on Electronic Computers . 9 (1): 39–47. doi :10.1109/TEC.1960.5221603.