Octaedro estrellado
 | |
| Tipo | Compuesto regular |
|---|---|
| Símbolo de Coxeter | {4,3}[2{3,3}]{3,4} [1] |
| Símbolos de Schläfli | {{3,3}} a{4,3} ß{2,4} ßr{2,2} |
| Diagramas de Coxeter |    ∪ ∪                  |
| Núcleo de estelación | octaedro regular |
| Casco convexo | Cubo |
| Índice | UC 4 , miércoles 19 |
| Poliedros | dos tetraedros |
| Caras | 8 triángulos |
| Bordes | 12 |
| Vértices | 8 |
| Poliedro dual | auto-dual |
| Grupo de simetría y grupo de Coxeter | O h , [4,3], orden 48 D 4h , [4,2], orden 16 D 2h , [2,2], orden 8 D 3d , [2 + ,6], orden 12 |
| Subgrupo restringido a un constituyente | T d , [3,3], orden 24 D 2d , [2 + ,4], orden 8 D 2 , [2,2] + , orden 4 C 3v , [3], orden 6 |

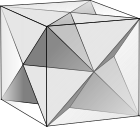
El octaedro estrellado es la única forma estelar del octaedro . También se le llama stella octangula (del latín «estrella de ocho puntas»), nombre que le dio Johannes Kepler en 1609, aunque ya era conocido por geómetras anteriores . Fue representado en De Divina Proportione de Pacioli , 1509. [2]
Es el más simple de los cinco compuestos poliédricos regulares y el único compuesto regular de dos tetraedros . También es el menos denso de los compuestos poliédricos regulares, con una densidad de 2.
Puede verse como una extensión 3D del hexagrama : el hexagrama es una forma bidimensional formada a partir de dos triángulos equiláteros superpuestos, simétricos centralmente entre sí, y de la misma manera el octaedro estrellado puede formarse a partir de dos tetraedros superpuestos simétricos centralmente. Esto se puede generalizar a cualquier cantidad deseada de dimensiones superiores; la construcción equivalente de cuatro dimensiones es el compuesto de dos celdas de 5. También se puede ver como una de las etapas en la construcción de un copo de nieve de Koch 3D , una forma fractal formada por la unión repetida de tetraedros más pequeños a cada cara triangular de una figura más grande. La primera etapa de la construcción del copo de nieve de Koch es un solo tetraedro central, y la segunda etapa, formada añadiendo cuatro tetraedros más pequeños a las caras del tetraedro central, es el octaedro estrellado.
Construcción
El octaedro estrellado se puede construir de varias maneras:
- Se trata de una estelación del octaedro regular , que comparte los mismos planos de las caras. (Ver modelo W 19 de Wenninger .)
 En perspectiva |  Plano de estelación | La única estelación de un octaedro regular, con un plano de estelación en amarillo. |
- También es un poliedro regular compuesto , cuando se construye como la unión de dos tetraedros regulares (un tetraedro regular y su tetraedro dual ).
- Se puede obtener como ampliación del octaedro regular , añadiendo pirámides tetraédricas en cada cara. En esta construcción tiene la misma topología que el sólido convexo de Catalan , el triakis octaedro , que tiene pirámides mucho más cortas.
- Se trata de un facetado del cubo , es decir, eliminar parte de las caras poligonales sin crear nuevos vértices de un cubo. [3]
- Puede verse como un antiprisma {4/2} ; siendo {4/2} un tetragrama, un compuesto de dos digones duales , y el tetraedro visto como un antiprisma digonal, este puede verse como un compuesto de dos antiprismas digonales .
- Puede verse como una red de una pirámide octaédrica de cuatro dimensiones , que consta de un octaedro central rodeado por ocho tetraedros.
 Facetado de un cubo | 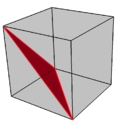 Un solo triángulo diagonal facetado en rojo |
Conceptos relacionados

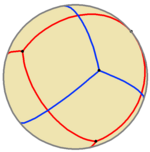
Se puede construir un compuesto de dos tetraedros esféricos, como se ilustra.
Los dos tetraedros de la visión compuesta del octaedro estrellado son "désmicos", lo que significa que (cuando se interpretan como una línea en el espacio proyectivo ) cada arista de un tetraedro cruza dos aristas opuestas del otro tetraedro. Uno de estos dos cruces es visible en el octaedro estrellado; el otro cruce ocurre en un punto en el infinito del espacio proyectivo, donde cada arista de un tetraedro cruza la arista paralela del otro tetraedro. Estos dos tetraedros pueden completarse para formar un sistema désmico de tres tetraedros, donde el tercer tetraedro tiene como sus cuatro vértices los tres puntos de cruce en el infinito y el centroide de los dos tetraedros finitos. Los mismos doce vértices del tetraedro también forman los puntos de la configuración de Reye .
Los números de la stella octangula son números figurados que cuentan la cantidad de bolas que se pueden colocar en forma de octaedro estrellado.
- 0, 1, 14, 51, 124, 245, 426, 679, 1016, 1449, 1990, .... (secuencia A007588 en la OEIS )
En la cultura popular
El octaedro estrellado aparece con varios otros poliedros y compuestos poliédricos en el grabado de MC Escher " Estrellas ", [4] y proporciona la forma central en el Planetoide Doble de Escher (1949). [5]
El obelisco en el centro de la Plaza de Europa en Zaragoza , España , está rodeado por doce farolas octaédricas estrelladas, diseñadas para formar una versión tridimensional de la Bandera de Europa . [6
Algunos místicos modernos han asociado esta forma con el "merkaba", [7] que según ellos es un "campo de energía contrarrotante" llamado así a partir de una antigua palabra egipcia. [8] Sin embargo, la palabra "merkaba" es en realidad hebrea , y se refiere más apropiadamente a un carro en las visiones de Ezequiel . [9] También se ha observado con frecuencia el parecido entre esta forma y la estrella bidimensional de David . [10]
El proyecto musical "Miracle Musical" (a menudo estilizado en su título original japonés ミラクルミュージカル, pronunciado "mirakuru myujikaru" [11] ), encabezado por el miembro de Tally Hall Joe Hawley junto con su compañero de banda Ross Federman y su compañero de banda honorario Bora Karaca, hace múltiples referencias al octaedro estrellado como stella octangula . La forma se muestra en el sitio web principal del proyecto, así como en la tienda de productos. [11] [12] La tercera canción de su primer y único álbum de estudio, "Hawaii: Part II", "Black Rainbows" presenta una letra cantada por Madi Diaz que simplemente dice "Stella octangula". [13]
Referencias
- ^ HSM Coxeter , Regular Polytopes , (3.ª edición, 1973), edición Dover, ISBN 0-486-61480-8 , 3.6 Los cinco compuestos regulares , págs. 47-50, 6.2 Estelando los sólidos platónicos , págs. 96-104
- ^ Barnes, John (2009), "Formas y sólidos", Gems of Geometry , Springer, págs. 25-56, doi :10.1007/978-3-642-05092-3_2, ISBN 978-3-642-05091-6.
- ^ Inchbald, Guy (2006), "Diagramas de facetas", The Mathematical Gazette , 90 (518): 253–261, doi :10.1017/S0025557200179653, JSTOR 40378613
- ^ Hart, George W. (1996), "Los poliedros de MC Escher", Poliedros virtuales.
- ^ Coxeter, HSM (1985), "Una reseña especial del libro: MC Escher: Su vida y su obra gráfica completa", The Mathematical Intelligencer , 7 (1): 59–69, doi :10.1007/BF03023010, S2CID 189887063. Véase en particular la pág. 61.
- ^ "Obelisco" [Obelisco], Zaragoza es Cultura (en español), Ayuntamiento de Zaragoza , consultado el 19 de octubre de 2021
- ^ Dannelley, Richard (1995), Sedona: más allá del vórtice: Activación del programa de ascensión planetaria con geometría sagrada, el vórtice y el Merkaba, Light Technology Publishing, pág. 14, ISBN 9781622336708
- ^ Melquisedec, Drunvalo (2000), El antiguo secreto de la Flor de la Vida: Una transcripción editada del Taller de la Flor de la Vida presentado en vivo a la Madre Tierra de 1985 a 1994 -, Volumen 1, Light Technology Publishing, pág. 4, ISBN 9781891824173
- ^ Patzia, Arthur G.; Petrotta, Anthony J. (2010), Diccionario de bolsillo de estudios bíblicos: Más de 300 términos definidos de forma clara y concisa, The IVP Pocket Reference Series, InterVarsity Press, pág. 78, ISBN 9780830867028
- ^ Brisson, David W. (1978), Hipergrafía: visualización de relaciones complejas en el arte, la ciencia y la tecnología , Westview Press para la Asociación Estadounidense para el Avance de la Ciencia, pág. 220,
La Stella octangula es el análogo tridimensional de la Estrella de David.
- ^ ab "ミ ラ ク ル ミ ュ ー ジ カ ル".ミ ラ ク ル ミ ュ ー ジ カ ル. Consultado el 9 de marzo de 2024 .
- ^ "Miracle Musical Store". Miracle Musical . Consultado el 9 de marzo de 2024 .
- ^ Miracle Musical (con Joe Hawley y Madi Diaz) – Black Rainbows , consultado el 9 de marzo de 2024
Enlaces externos
- Weisstein, Eric W. , "Stella Octangula" ("Compuesto de dos tetraedros") en MathWorld .
- Klitzing, Richard, "Compuesto 3D"
