Número triangular cuadrado

En teoría de números , la suma de los primeros n cubos es el cuadrado del n- ésimo número triangular . Es decir,

${\displaystyle 1^{3}+2^{3}+3^{3}+\cdots +n^{3}=\left(1+2+3+\cdots +n\right)^{2}.}$

La misma ecuación se puede escribir de forma más compacta utilizando la notación matemática para la suma :

${\displaystyle \suma _{k=1}^{n}k^{3}=\left(\suma _{k=1}^{n}k\right)^{2}.}$

Esta identidad a veces se denomina teorema de Nicómaco , en honor a Nicómaco de Gerasa ( c.  60 – c.  120 d. C. ).

Nicómaco, al final del capítulo 20 de su Introducción a la aritmética , señaló que si uno escribe una lista de los números impares, el primero es el cubo de 1, la suma de los dos siguientes es el cubo de 2, la suma de los tres siguientes es el cubo de 3, y así sucesivamente. No va más allá de esto, pero de esto se sigue que la suma de los primeros n cubos es igual a la suma de los primeros ⁠n ( n +1)/2⁠ números impares, es decir, los números impares del 1 al n ( n + 1) − 1 . El promedio de estos números es obviamente ⁠n ( n +1)/2⁠ , y hay ⁠n ( n +1)/2⁠ de ellos, por lo que su suma es ( ⁠n ( n +1)/2⁠ ) ^​​2 .

Muchos matemáticos antiguos han estudiado y proporcionado pruebas del teorema de Nicómaco. Stroeker (1995) afirma que "todo estudiante de teoría de números seguramente debe haberse maravillado ante este hecho milagroso". Pengelley (2002) encuentra referencias a la identidad no solo en las obras de Nicómaco en lo que ahora es Jordania en el siglo I d.C., sino también en las de Aryabhata en la India en el siglo V, y en las de Al-Karaji c.  1000 en Persia . Bressoud (2004) menciona varias obras matemáticas tempranas adicionales sobre esta fórmula, por Al-Qabisi (siglo X, Arabia), Gersonides ( c.  1300 , Francia) y Nilakantha Somayaji ( c.  1500 , India); reproduce la prueba visual de Nilakantha.

La secuencia de números triangulares cuadrados es ^[1]

Estos números pueden verse como números figurados , una generalización hiperpiramidal de cuatro dimensiones de los números triangulares y los números piramidales cuadrados .

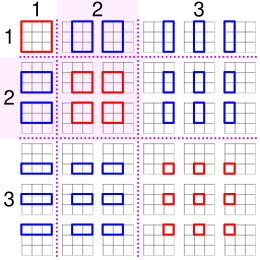
Como observa Stein (1971), estos números también cuentan el número de rectángulos con lados horizontales y verticales formados en una cuadrícula de n × n . Por ejemplo, los puntos de una cuadrícula de 4 × 4 (o un cuadrado formado por tres cuadrados más pequeños en un lado) pueden formar 36 rectángulos diferentes. El número de cuadrados en una cuadrícula cuadrada se cuenta de manera similar mediante los números piramidales cuadrados.

La identidad también admite una interpretación probabilística natural como sigue. Sean X , Y , Z , W cuatro números enteros elegidos de forma independiente y uniforme al azar entre 1 y n . Entonces, la probabilidad de que W sea el mayor de los cuatro números es igual a la probabilidad de que Y sea al menos tan grande como X y de que W sea al menos tan grande como Z . Es decir, P [max( X , Y , Z ) ≤ W ] = P [ X ≤ Y ∧ Z ≤ W ] . Para cualquier valor particular de W , las combinaciones de X , Y y Z que hacen que W sea el más grande forman un cubo 1 ≤  X , Y , Z ≤ n por lo que (sumando el tamaño de este cubo sobre todas las opciones de W ) el número de combinaciones de X , Y , Z , W para las que W es el más grande es una suma de cubos, el lado izquierdo de la identidad de Nicómaco. Los conjuntos de pares ( X , Y ) con X ≤ Y y de pares ( Z , W ) con Z ≤ W forman triángulos rectángulos isósceles, y el conjunto contado por el lado derecho de la ecuación de probabilidades es el producto cartesiano de estos dos triángulos, por lo que su tamaño es el cuadrado de un número triangular en el lado derecho de la identidad de Nicómaco. Las probabilidades en sí mismas son respectivamente los lados izquierdo y derecho de la identidad de Nicómaco, normalizadas para formar probabilidades dividiendo ambos lados por  n ⁴ . ^{[ cita requerida ]}

Charles Wheatstone  (1854) ofrece una derivación particularmente sencilla, al expandir cada cubo de la suma en un conjunto de números impares consecutivos. Comienza dando la identidad Esa identidad está relacionada con los números triangulares T _n de la siguiente manera: y, por lo tanto, los sumandos que forman n ³ comienzan justo después de los que forman todos los valores anteriores 1 ³ hasta ( n − 1) ³ . La aplicación de esta propiedad, junto con otra identidad bien conocida: produce la siguiente derivación:$${\displaystyle n^{3}=\underbrace {\left(n^{2}-n+1\right)+\left(n^{2}-n+1+2\right)+\left(n^{2}-n+1+4\right)+\cdots +\left(n^{2}+n-1\right)} _{n{\text{ números impares consecutivos}}}.}$$ $${\displaystyle n^{3}=\sum _{k=T_{n-1}+1}^{T_{n}}(2k-1),}$$$${\displaystyle n^{2}=\suma _{k=1}^{n}(2k-1),}$$$${\displaystyle {\begin{aligned}\sum _{k=1}^{n}k^{3}&=1+8+27+64+\cdots +n^{3}\\&=\underbrace {1} _{1^{3}}+\underbrace {3+5} _{2^{3}}+\underbrace {7+9+11} _{3^{3}}+\underbrace {13+15+17+19} _{4^{3}}+\cdots +\underbrace {\left(n^{2}-n+1\right)+\cdots +\left(n^{2}+n-1\right)} _{n^{3}}\\&=\underbrace {\underbrace {\underbrace {\underbrace {1} _{1^{2}}+3} _{2^{2}}+5} _{3^{2}}+\cdots +\left(n^{2}+n-1\right)} _{\left({\frac {n^{2}+n}{2}}\right)^{2}}\\&=(1+2+\cdots +n)^{2}\\&=\left(\sum _{k=1}^{n}k\right)^{2}.\end{aligned}}}$$

Row (1893) obtiene otra prueba sumando los números de una tabla de multiplicación cuadrada de dos maneras diferentes. La suma de la i- ésima fila es i por un número triangular, de lo que se sigue que la suma de todas las filas es el cuadrado de un número triangular. Alternativamente, se puede descomponer la tabla en una secuencia de gnomones anidados , cada uno de los cuales consiste en los productos en los que el mayor de los dos términos es un valor fijo. La suma dentro de cada gmonon es un cubo, por lo que la suma de toda la tabla es una suma de cubos.

En la literatura matemática más reciente, Edmonds (1957) proporciona una prueba utilizando la suma por partes . Stein (1971) utiliza la interpretación de conteo de rectángulos de estos números para formar una prueba geométrica de la identidad (véase también Benjamin, Quinn y Wurtz 2006); observa que también se puede demostrar fácilmente (pero de manera poco informativa) por inducción, y afirma que Toeplitz (1963) proporciona "una antigua prueba árabe interesante". Kanim (2004) proporciona una prueba puramente visual, Benjamin y Orrison (2002) proporcionan dos pruebas adicionales, y Nelsen (1993) da siete pruebas geométricas.

Un resultado similar al del teorema de Nicómaco se aplica a todas las sumas de potencias , es decir, que las sumas de potencias impares (sumas de potencias impares) son un polinomio en números triangulares. Se denominan polinomios de Faulhaber , de los cuales la suma de cubos es el ejemplo más simple y elegante. Sin embargo, en ningún otro caso una suma de potencias es el cuadrado de otra. ^[2]

Stroeker (1995) estudia condiciones más generales en las que la suma de una secuencia consecutiva de cubos forma un cuadrado. Garrett y Hummel (2004) y Warnaar (2004) estudian análogos polinómicos de la fórmula del número triangular cuadrado, en la que una serie de polinomios se suma al cuadrado de otro polinomio.

• Weisstein, Eric W. , "Teorema de Nicómaco", MathWorld
• Una prueba visual del teorema de Nicómaco Archivado el 19 de octubre de 2019 en Wayback Machine.