Teorema de las capas

En mecánica clásica , el teorema de las capas ofrece simplificaciones gravitacionales que se pueden aplicar a objetos dentro o fuera de un cuerpo con simetría esférica . Este teorema tiene una aplicación particular en astronomía .

Isaac Newton demostró el teorema de las capas ^[1] y afirmó que:

1. Un cuerpo esféricamente simétrico afecta a los objetos externos gravitacionalmente como si toda su masa estuviera concentrada en un punto en su centro.
2. Si el cuerpo es una cáscara esféricamente simétrica (es decir, una bola hueca), la cáscara no ejerce ninguna fuerza gravitacional neta sobre ningún objeto en su interior, independientemente de la ubicación del objeto dentro de la cáscara.

Un corolario es que dentro de una esfera sólida de densidad constante, la fuerza gravitatoria dentro del objeto varía linealmente con la distancia desde el centro, volviéndose cero por simetría en el centro de masa . Esto se puede ver de la siguiente manera: tome un punto dentro de dicha esfera, a una distancia del centro de la esfera. Entonces puede ignorar todas las capas de radio mayor, de acuerdo con el teorema de capas (2). Pero el punto puede considerarse externo a la esfera restante de radio r, y de acuerdo con (1) toda la masa de esta esfera puede considerarse concentrada en su centro. La masa restante es proporcional a (porque se basa en el volumen). La fuerza gravitatoria ejercida sobre un cuerpo de radio r será proporcional a (la ley del cuadrado inverso ), por lo que el efecto gravitatorio general es proporcional a , por lo que es lineal en .${\estilo de visualización r}$${\estilo de visualización m}$${\estilo de visualización r^{3}}$$Estilo de visualización m/r^{2}}$${\displaystyle r^{3}/r^{2}=r}$${\estilo de visualización r}$

Estos resultados fueron importantes para el análisis de Newton del movimiento planetario; no son inmediatamente obvios, pero pueden demostrarse con cálculo . ( La ley de Gauss para la gravedad ofrece una forma alternativa de enunciar el teorema).

Además de la gravedad , el teorema de las capas también se puede utilizar para describir el campo eléctrico generado por una densidad de carga estática con simetría esférica , o de manera similar para cualquier otro fenómeno que siga una ley del cuadrado inverso . Las derivaciones a continuación se centran en la gravedad, pero los resultados se pueden generalizar fácilmente a la fuerza electrostática .

Hay tres pasos para demostrar el teorema de capas de Newton (1). Primero, se derivará la ecuación para un campo gravitatorio debido a un anillo de masa. Al organizar un número infinito de anillos infinitamente delgados para formar un disco, esta ecuación que involucra un anillo se utilizará para encontrar el campo gravitatorio debido a un disco. Finalmente, al organizar un número infinito de discos infinitamente delgados para formar una esfera, esta ecuación que involucra un disco se utilizará para encontrar el campo gravitatorio debido a una esfera.

El campo gravitacional en una posición llamada en el eje x debido a un punto de masa en el origen es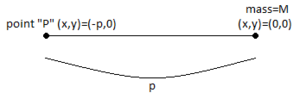${\estilo de visualización E}$${\estilo de visualización P}$${\displaystyle (x,y)=(-p,0)}$${\estilo de visualización M}$$${\displaystyle E_{\text{punto}}={\frac {GM}{p^{2}}}}$$Supongamos que esta masa se mueve hacia arriba a lo largo del eje y hasta el punto . La distancia entre y la masa puntual es ahora mayor que antes; se convierte en la hipotenusa del triángulo rectángulo con catetos y que es . Por lo tanto, el campo gravitatorio del punto elevado es: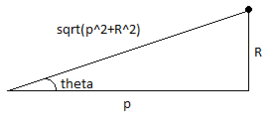${\estilo de visualización (-p,R)}$${\estilo de visualización P}$${\estilo de visualización p}$${\estilo de visualización R}$${\estilo de texto {\sqrt {p^{2}+R^{2}}}}$$${\displaystyle E_{\text{punto elevado}}={\frac {GM}{p^{2}+R^{2}}}}$$

La magnitud del campo gravitatorio que atraería a una partícula en el punto en la dirección x es el campo gravitatorio multiplicado por donde es el ángulo adyacente al eje x . En este caso, . Por lo tanto, la magnitud del campo gravitatorio en la dirección x , es: Sustituyendo en da Supongamos que esta masa está distribuida uniformemente en un anillo centrado en el origen y orientado hacia el punto con el mismo radio . Debido a que toda la masa se encuentra en el mismo ángulo con respecto al eje x , y la distancia entre los puntos en el anillo es la misma distancia que antes, el campo gravitatorio en la dirección x en el punto debido al anillo es el mismo que una masa puntual ubicada en un punto unidades por encima del eje y :${\estilo de visualización P}$${\displaystyle \cos(\theta )}$${\estilo de visualización \theta}$${\displaystyle \cos(\theta )={\frac {p}{\sqrt {p^{2}+R^{2}}}}}$$Estilo de visualización E_{x}}$$${\displaystyle E_{x}={\frac {GM\cos {\theta }}{p^{2}+R^{2}}}}$$${\displaystyle \cos(\theta )}$$${\displaystyle E_{x}={\frac {GMp}{\left(p^{2}+R^{2}\right)^{3/2}}}}$$${\estilo de visualización P}$${\estilo de visualización R}$${\estilo de visualización P}$${\estilo de visualización R}$$${\displaystyle E_{\text{anillo}}={\frac {GMp}{\left(p^{2}+R^{2}\right)^{3/2}}}}$$

Para hallar el campo gravitatorio en el punto debido a un disco, se puede colocar un número infinito de anillos infinitamente delgados enfrentados , cada uno con un radio de , un ancho de , y una masa de , uno dentro del otro para formar un disco. La masa de cualquiera de los anillos es la masa del disco multiplicada por la relación entre el área del anillo y el área total del disco . Por lo tanto, . Por lo tanto, un pequeño cambio en el campo gravitatorio, es:${\estilo de visualización P}$${\estilo de visualización P}$${\estilo de visualización y}$${\estilo de visualización dy}$${\estilo de visualización dM}$${\estilo de visualización dM}$${\displaystyle 2\pi y\,dy}$$Estilo de visualización: \pi R^{2}$${\textstyle dM={\frac {M\cdot 2y\,dy}{R^{2}}}}$${\estilo de visualización E}$$${\displaystyle dE={\frac {Gp\,dM}{(p^{2}+y^{2})^{3/2}}}}$$

Sustituyendo e integrando ambos lados se obtiene el campo gravitacional del disco: Sumando la contribución al campo gravitacional de cada uno de estos anillos se obtendrá la expresión para el campo gravitacional debido a un disco. Esto es equivalente a integrar esta expresión anterior de a , lo que da como resultado: Para encontrar el campo gravitacional en el punto debido a una esfera centrada en el origen, se pueden colocar juntos una cantidad infinita de discos infinitamente delgados orientados hacia , cada uno con un radio de , un ancho de , y una masa de .${\estilo de visualización dM}$$${\displaystyle E=\int {\frac {GMp\cdot {\frac {2y\,dy}{R^{2}}}}{(p^{2}+y^{2})^{3/2}}}}$$${\displaystyle y=0}$${\displaystyle y=R}$$${\displaystyle E_{\text{disco}}={\frac {2GM}{R^{2}}}\left(1-{\frac {p}{\sqrt {p^{2}+R^{2}}}}\right)}$$${\estilo de visualización P}$${\estilo de visualización P}$${\estilo de visualización R}$${\estilo de visualización dx}$${\estilo de visualización dM}$

Los radios de estos discos siguen la altura de la sección transversal de una esfera (con radio constante ) que es una ecuación de un semicírculo: . varía de a .${\estilo de visualización R}$${\estilo de visualización a}$${\textstyle R={\sqrt {a^{2}-x^{2}}}}$ ${\estilo de visualización x}$${\estilo de visualización -a}$${\estilo de visualización a}$

La masa de cualquiera de los discos es la masa de la esfera multiplicada por la relación entre el volumen de un disco infinitamente delgado dividido por el volumen de una esfera (con radio constante ). El volumen de un disco infinitamente delgado es , o . Por lo tanto, .  Simplificando obtenemos .${\estilo de visualización dM}$${\estilo de visualización M}$${\estilo de visualización a}$$estilo de visualización \pi R^{2}\,dx$${\textstyle \pi \left(a^{2}-x^{2}\right)dx}$${\textstyle dM={\frac {\pi M(a^{2}-x^{2})\,dx}{{\frac {4}{3}}\pi a^{3}}}}$${\textstyle dM={\frac {3M(a^{2}-x^{2})\,dx}{4a^{3}}}}$

La posición de cada disco variará según su posición dentro de la "esfera" formada por los discos, por lo que debe reemplazarse con .${\estilo de visualización P}$${\estilo de visualización p}$${\estilo de visualización p+x}$

Reemplazando con , con y con en la ecuación del 'disco' se obtiene: Simplificando, integrando el campo gravitacional de cada disco delgado de a con respecto a y haciendo un poco de álgebra cuidadosa, se obtiene el teorema de las capas de Newton: donde es la distancia entre el centro de la masa esférica y un punto arbitrario .  El campo gravitacional de una masa esférica se puede calcular tratando toda la masa como una partícula puntual en el centro de la esfera.${\estilo de visualización M}$${\estilo de visualización dM}$ ${\estilo de visualización R}$${\displaystyle {\sqrt {a^{2}-x^{2}}}}$${\estilo de visualización p}$${\estilo de visualización p+x}$$${\displaystyle dE={\frac {\left({\frac {2G\left[3M\left(a^{2}-x^{2}\right)\right]}{4a^{3}}}\right)}{{\sqrt {a^{2}-x^{2}}}^{2}}}\cdot \left(1-{\frac {p+x}{\sqrt {(p+x)^{2}+{\sqrt {a^{2}-x^{2}}}^{2}}}}\right)\,dx}$$$${\displaystyle \int dE=\int _{-a}^{a}{\frac {3GM}{2a^{3}}}(1-{\frac {p+x}{\sqrt {p^{2}+a^{2}+2px}}}\right)dx}$$${\displaystyle x=-a}$${\displaystyle x=+a}$${\estilo de visualización x}$$${\displaystyle E={\frac {GM}{p^{2}}}}$$${\estilo de visualización p}$${\estilo de visualización P}$

Un cuerpo sólido, simétrico desde el punto de vista esférico , puede modelarse como un número infinito de capas esféricas concéntricas , infinitesimalmente delgadas. Si una de estas capas puede tratarse como una masa puntual, entonces un sistema de capas (es decir, la esfera) también puede tratarse como una masa puntual. Consideremos una de estas capas (el diagrama muestra una sección transversal):

(Nota: en el diagrama se refiere al ángulo pequeño, no a la longitud del arco . La longitud del arco es ).${\estilo de visualización d\theta}$${\textstyle R\,d\theta }$

Aplicando la Ley de Gravitación Universal de Newton , la suma de las fuerzas debidas a los elementos de masa en la banda sombreada es

${\displaystyle dF={\frac {Gm}{s^{2}}}dM.}$

Sin embargo, dado que hay una cancelación parcial debido a la naturaleza vectorial de la fuerza junto con la simetría de la banda circular, el componente restante (en la dirección que apunta hacia ) está dado por${\estilo de visualización m}$

${\displaystyle dF_{r}={\frac {Gm}{s^{2}}}\cos(\varphi )\,dM}$

La fuerza total sobre , entonces, es simplemente la suma de la fuerza ejercida por todas las bandas. Al reducir el ancho de cada banda y aumentar el número de bandas, la suma se convierte en una expresión integral:${\displaystyle m}$

${\displaystyle F_{r}=\int dF_{r}}$

Como y son constantes, se pueden sacar de la integral:${\displaystyle G}$${\displaystyle m}$

${\displaystyle F_{r}=Gm\int {\frac {\cos(\varphi )}{s^{2}}}\,dM.}$

Para evaluar esta integral, primero se debe expresar como una función de${\displaystyle dM}$${\displaystyle d\theta }$

La superficie total de una carcasa esférica es

${\displaystyle 4\pi R^{2}}$

mientras que el área de superficie de la rebanada delgada entre y es${\displaystyle \theta }$${\displaystyle \theta +d\theta }$

${\displaystyle 2\pi R\sin(\theta )R\,d\theta =2\pi R^{2}\sin(\theta )\,d\theta }$

Si la masa de la concha es , entonces se tiene que${\displaystyle M}$

${\displaystyle dM={\frac {2\pi R^{2}\sin(\theta )}{4\pi R^{2}}}M\,d\theta ={\frac {1}{2}}M\sin(\theta )\,d\theta }$

y

${\displaystyle F_{r}={\frac {GMm}{2}}\int {\frac {\sin(\theta )\cos(\varphi )}{s^{2}}}\,d\theta }$

Por la ley de los cosenos ,

${\displaystyle \cos(\varphi )={\frac {r^{2}+s^{2}-R^{2}}{2rs}}}$

y

${\displaystyle \cos(\theta )={\frac {r^{2}+R^{2}-s^{2}}{2rR}}.}$

Estas dos relaciones vinculan los tres parámetros , y que aparecen en la integral juntos. A medida que aumenta de a radianes, varía desde el valor inicial 0 hasta un valor máximo antes de volver finalmente a cero en . Al mismo tiempo, aumenta desde el valor inicial hasta el valor final a medida que aumenta de 0 a radianes. Esto se ilustra en la siguiente animación:${\displaystyle \theta }$ ${\displaystyle \varphi }$${\displaystyle s}$${\displaystyle \theta }$${\displaystyle 0}$${\displaystyle \pi }$${\displaystyle \varphi }$${\displaystyle \theta =\pi }$${\displaystyle s}$${\displaystyle r-R}$${\displaystyle r+R}$${\displaystyle \theta }$${\displaystyle \pi }$

(Nota: Visto desde , la banda azul sombreada aparece como un anillo delgado cuyos radios interno y externo convergen hacia un punto en el que se desvanecen).${\displaystyle m}$${\displaystyle R\sin(\theta )}$${\displaystyle d\theta }$

Para encontrar una función primitiva para el integrando, hay que hacer que la variable de integración sea independiente en lugar de .${\displaystyle s}$${\displaystyle \theta }$

Realizando una diferenciación implícita de la segunda de las expresiones de la "ley del coseno" anteriores obtenemos

${\displaystyle -\sin(\theta )\,d\theta ={\frac {-2s}{2rR}}\,ds}$

y por lo tanto

${\displaystyle \sin(\theta )\,d\theta ={\frac {s}{rR}}\,ds.}$

Resulta que

${\displaystyle F_{r}={\frac {GMm}{2}}{\frac {1}{rR}}\int {\frac {s\cos(\varphi )}{s^{2}}}\,ds={\frac {GMm}{2rR}}\int {\frac {\cos(\varphi )}{s}}\,ds}$

donde la nueva variable de integración aumenta de a .${\displaystyle s}$${\displaystyle r-R}$ ${\displaystyle r+R}$

Insertando la expresión para usar la primera de las expresiones de la "ley del coseno" anteriores, finalmente se obtiene que${\displaystyle \cos(\varphi )}$

${\displaystyle F_{r}={\frac {GMm}{4r^{2}R}}\int \left(1+{\frac {r^{2}-R^{2}}{s^{2}}}\right)\ ds\ .}$

Una función primitiva para el integrando es

${\displaystyle s-{\frac {r^{2}-R^{2}}{s}}\ ,}$

e insertando los límites y para la variable de integración en esta función primitiva, se obtiene que${\displaystyle r-R}$${\displaystyle r+R}$${\displaystyle s}$

${\displaystyle F_{r}={\frac {GMm}{r^{2}}},}$

diciendo que la fuerza gravitacional es la misma que la de una masa puntual en el centro de la capa con la misma masa.

Es posible utilizar este resultado de la capa esférica para volver a derivar el resultado de la esfera sólida obtenido anteriormente. Esto se hace integrando una capa esférica infinitesimalmente delgada con una masa de , y podemos obtener la contribución gravitatoria total de una bola sólida al objeto que se encuentra fuera de la bola.${\displaystyle dM}$

${\displaystyle F_{total}=\int dF_{r}={\frac {Gm}{r^{2}}}\int dM.}$

La densidad uniforme significa entre el radio de a , puede expresarse como una función de , es decir,${\displaystyle x}$${\displaystyle x+dx}$ ${\displaystyle dM}$${\displaystyle x}$

${\displaystyle dM={\frac {4\pi x^{2}dx}{{\frac {4}{3}}\pi R^{3}}}M={\frac {3Mx^{2}dx}{R^{3}}}}$

Por lo tanto, la gravedad total es

${\displaystyle F_{\text{total}}={\frac {3GMm}{r^{2}R^{3}}}\int _{0}^{R}x^{2}\,dx={\frac {GMm}{r^{2}}}}$

Como se encontró anteriormente, esto sugiere que la gravedad de una bola esférica sólida hacia un objeto exterior se puede simplificar como la de una masa puntual en el centro de la bola con la misma masa.

Para un punto dentro de la capa, la diferencia es que cuando θ es igual a cero, ϕ toma el valor π radianes y s el valor R − r . Cuando θ aumenta de 0 a π radianes, ϕ disminuye desde el valor inicial π radianes hasta cero y s aumenta desde el valor inicial R − r hasta el valor R + r .

Todo esto se puede ver en la siguiente figura.

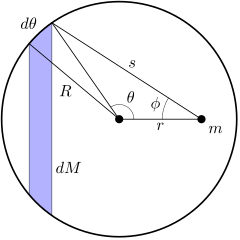
Insertar estos límites en la función primitiva

${\displaystyle s-{\frac {r^{2}-R^{2}}{s}}}$

Uno consigue que, en este caso

${\displaystyle F_{r}=0,}$

diciendo que las fuerzas gravitacionales netas que actúan sobre la masa puntual desde los elementos de masa de la capa, fuera del punto de medición, se cancelan.

Generalización: Si , la fuerza resultante dentro de la carcasa es:${\displaystyle f={\frac {k}{r^{p}}}}$

${\displaystyle F(r)={\frac {GMm}{4r^{2}R}}\int _{R-r}^{R+r}\left({\frac {1}{s^{p-2}}}+{\frac {r^{2}-R^{2}}{s^{p}}}\right)\,ds}$

Los resultados anteriores son idénticos a cero si y solo si${\displaystyle F(r)}$${\displaystyle p=2}$

Fuera de la concha (es decir o ):${\displaystyle r>R}$${\displaystyle r<-R}$

${\displaystyle F(r)={\frac {GMm}{4r^{2}R}}\int _{r-R}^{r+R}\left({\frac {1}{s^{p-2}}}+{\frac {r^{2}-R^{2}}{s^{p}}}\right)\,ds}$

El teorema de las capas es una consecuencia inmediata de la ley de Gauss para la gravedad, que dice que

${\displaystyle \int _{S}{\mathbf {g} }\cdot \,d{\mathbf {S} }=-4\pi GM}$

donde M es la masa de la parte de la distribución de masa esféricamente simétrica que está dentro de la esfera con radio r y

${\displaystyle \int _{S}{\mathbf {g} }\cdot \,d{\mathbf {S} }=\int _{S}{\mathbf {g} }\cdot {\hat {\mathbf {n} }}\,dS}$

es la integral de superficie del campo gravitacional sobre cualquier superficie cerrada dentro de la cual la masa total es M , siendo el vector unitario la normal externa a la superficie.${\displaystyle \mathbf {g} }$ ${\displaystyle {\hat {\mathbf {n} }}}$

El campo gravitatorio de una distribución de masa esféricamente simétrica, como un punto de masa, una envoltura esférica o una esfera homogénea, también debe ser esféricamente simétrico. Si es un vector unitario en la dirección desde el punto de simetría hasta otro punto, el campo gravitatorio en este otro punto debe ser${\displaystyle {\hat {\mathbf {n} }}}$

${\displaystyle \mathbf {g} =g(r){\hat {\mathbf {n} }}}$

donde g ( r ) sólo depende de la distancia r al punto de simetría

Seleccionando la superficie cerrada como una esfera con radio r con centro en el punto de simetría, la normal externa a un punto en la superficie, , es precisamente la dirección que apunta lejos del punto de simetría de la distribución de masa.${\displaystyle {\hat {\mathbf {n} }}}$

Por lo tanto, se tiene que

${\displaystyle \mathbf {g} =g(r){\hat {\mathbf {n} }}}$

y

${\displaystyle \int _{S}\mathbf {g} \cdot \,d{\mathbf {S} }=g(r)\int _{S}\,dS=g(r)4\pi r^{2}}$

como el área de la esfera es 4 π r ² .

De la ley de Gauss se deduce que

${\displaystyle g(r)4\pi r^{2}=-4\pi GM,}$

o,

${\displaystyle g(r)=-{\frac {GM}{r^{2}}}.}$

Es natural preguntarse si el recíproco del teorema de las capas es cierto, es decir, si el resultado del teorema implica la ley de la gravitación universal, o si existe alguna ley de fuerza más general para la que se cumple el teorema. Más concretamente, se puede plantear la pregunta:

Supóngase que existe una fuerza entre las masas M y m , separadas por una distancia r, de la forma tal que cualquier cuerpo esféricamente simétrico afecta a los cuerpos externos como si su masa estuviera concentrada en su centro. Entonces, ¿qué forma puede adoptar la función ?${\displaystyle F}$${\displaystyle F=Mmf(r)}$${\displaystyle f}$

De hecho, esto permite exactamente una clase más de fuerza que el cuadrado inverso (newtoniano). ^{[2] [3]} La fuerza más general derivada por Vahe Gurzadyan en ^[2] el teorema de Gurzadyan es:

${\displaystyle F=-{\frac {GMm}{r^{2}}}+{\frac {\Lambda mc^{2}r}{3}}}$

donde y pueden ser constantes que toman cualquier valor. El primer término es la conocida ley de gravitación universal; el segundo es una fuerza adicional, análoga al término de constante cosmológica en la relatividad general .${\displaystyle G}$${\displaystyle \Lambda }$

Si restringimos aún más la fuerza al exigir que también se cumpla la segunda parte del teorema, es decir, que no hay fuerza dentro de una bola hueca, excluimos la posibilidad del término adicional y la ley del cuadrado inverso es de hecho la única ley de fuerza que satisface el teorema.

Por otra parte, si relajamos las condiciones y sólo requerimos que el campo en todas partes fuera de un cuerpo esféricamente simétrico sea el mismo que el campo desde algún punto de masa en el centro (de cualquier masa), permitimos una nueva clase de soluciones dadas por el potencial de Yukawa , del cual la ley del cuadrado inverso es un caso especial.

Se puede hacer otra generalización para un disco observando que

${\displaystyle dM={\frac {R^{2}}{2}}{\frac {d\theta \,\sin ^{2}(\theta )}{\pi R^{2}}}M={\frac {\sin ^{2}(\theta )}{2\pi }}M\,d\theta }$

entonces:

${\displaystyle F_{r}={\frac {GMm}{2\pi }}\int {\frac {\sin ^{2}(\theta )\cos(\varphi )}{s^{2}}}\,d\theta ,}$

donde , y es la densidad del cuerpo.${\displaystyle M=\pi R^{2}\rho }$${\displaystyle \rho }$

Haciendo todos los cálculos intermedios obtenemos:

${\displaystyle F(r)={\frac {Gm\rho }{8r^{3}}}\int _{R-r}^{R+r}{\frac {\left(r^{2}+s^{2}-R^{2}\right){\sqrt {2\left(r^{2}R^{2}+r^{2}s^{2}+R^{2}s^{2}\right)-s^{4}-r^{4}-R^{4}}}}{s^{2}}}\,ds}$

Las proposiciones 70 y 71 consideran la fuerza que actúa sobre una partícula desde una esfera hueca con una superficie infinitesimalmente delgada, cuya densidad de masa es constante sobre la superficie. La fuerza sobre la partícula desde un área pequeña de la superficie de la esfera es proporcional a la masa del área e inversamente proporcional al cuadrado de su distancia a la partícula. La primera proposición considera el caso en el que la partícula está dentro de la esfera, la segunda cuando está fuera. El uso de infinitesimales y procesos limitantes en construcciones geométricas son simples y elegantes y evitan la necesidad de cualquier integración. Ilustran bien el método de Newton para probar muchas de las proposiciones de los Principia .

Su demostración de la proposición 70 es trivial. A continuación, se la analiza con un poco más de detalle que el que ofrece Newton.

La prueba de la Proposición 71 es más significativa desde el punto de vista histórico. Constituye la primera parte de su prueba de que la fuerza gravitatoria de una esfera sólida que actúa sobre una partícula situada fuera de ella es inversamente proporcional al cuadrado de su distancia al centro de la esfera, siempre que la densidad en cualquier punto del interior de la esfera sea una función únicamente de su distancia al centro de la esfera.

Aunque las siguientes son completamente fieles a las pruebas de Newton, se han realizado cambios muy pequeños para intentar hacerlas más claras.

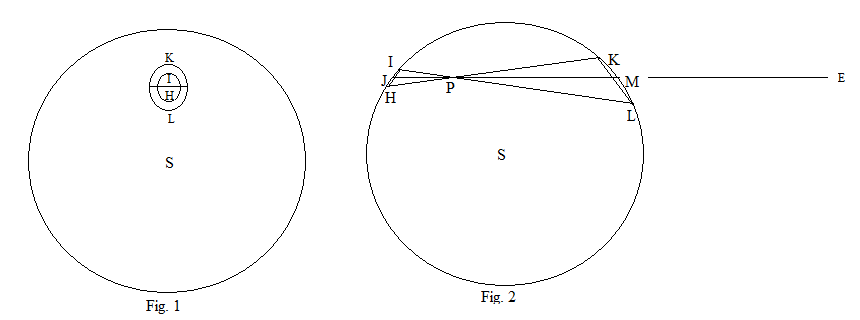
La figura 2 es una sección transversal de la esfera hueca a través del centro, S y un punto arbitrario, P, dentro de la esfera. A través de P, traza dos líneas IL y HK de modo que el ángulo KPL sea muy pequeño. JM es la línea que pasa por P y divide en dos ese ángulo. Del teorema del ángulo inscrito , los triángulos IPH y KPL son semejantes. Las líneas KH e IL se rotan sobre el eje JM para formar dos conos que intersecan la esfera en dos curvas cerradas. En la figura 1, la esfera se ve desde una distancia a lo largo de la línea PE y se supone transparente, de modo que se pueden ver ambas curvas.

La superficie de la esfera que intersecan los conos puede considerarse plana, y .${\displaystyle \angle PJI=\angle PMK}$

Como la intersección de un cono con un plano es una elipse, en este caso las intersecciones forman dos elipses con ejes mayores IH y KL, donde .${\displaystyle {\frac {IH}{KL}}={\frac {PJ}{PM}}}$

Por un argumento similar, los ejes menores están en la misma proporción. Esto es claro si la esfera se ve desde arriba. Por lo tanto, las dos elipses son similares, por lo que sus áreas son como los cuadrados de sus ejes mayores. Como la masa de cualquier sección de la superficie es proporcional al área de esa sección, para las dos áreas elípticas las razones de sus masas son .${\displaystyle \propto {\frac {PJ^{2}}{PM^{2}}}}$

Como la fuerza de atracción sobre P en la dirección JM desde cualquiera de las áreas elípticas es directa como la masa del área e inversamente proporcional al cuadrado de su distancia a P, es independiente de la distancia de P a la esfera. Por lo tanto, las fuerzas sobre P desde las dos áreas elípticas infinitesimales son iguales y opuestas y no hay ninguna fuerza neta en la dirección JM.

Como la posición de P y la dirección de JM son ambas arbitrarias, se deduce que cualquier partícula dentro de una esfera hueca no experimenta ninguna fuerza neta de la masa de la esfera.

Nota: Newton simplemente describe los arcos IH y KL como "mínimamente pequeños" y las áreas trazadas por las líneas IL y HK pueden tener cualquier forma, no necesariamente elípticas, pero siempre serán similares.

La figura 1 es una sección transversal de la esfera hueca a través del centro, S con un punto arbitrario, P, fuera de la esfera. PT es la tangente al círculo en T que pasa por P. HI es un pequeño arco en la superficie tal que PH es menor que PT. Extiende PI para intersecar la esfera en L y dibuja SF hasta el punto F que biseca a IL. Extiende PH para intersecar la esfera en K y dibuja SE hasta el punto E que biseca a HK, y extiende SF para intersecar a HK en D. Traza una perpendicular IQ sobre la línea PS que une P con el centro S. Sea a el radio de la esfera y D la distancia PS.

Sea el arco IH prolongado perpendicularmente fuera del plano del diagrama, por una pequeña distancia ζ. El área de la figura generada es , y su masa es proporcional a este producto.${\displaystyle IH\cdot \zeta }$

La fuerza debida a esta masa sobre la partícula en P y está a lo largo de la línea PI. ${\displaystyle \propto {\frac {IH\cdot \zeta }{PI^{2}}}}$

El componente de esta fuerza hacia el centro .${\displaystyle \propto {\frac {IH\cdot PQ\cdot \zeta }{PI^{3}}}}$

Si ahora el arco HI se gira completamente alrededor de la línea PS para formar un anillo de ancho HI y radio IQ , la longitud del anillo es 2 π · IQ y su área es 2 π · IQ · IH . El componente de la fuerza debida a este anillo sobre la partícula en P en la dirección PS se convierte en .${\displaystyle \propto {\frac {IH\cdot IQ\cdot PQ}{PI^{3}}}}$

Las componentes perpendiculares de la fuerza dirigida hacia PS se cancelan, ya que la masa en el anillo se distribuye simétricamente con respecto a PS . Por lo tanto, la componente en la dirección PS es la fuerza total sobre P debida al anillo formado al girar el arco HI con respecto a PS .

De triángulos semejantes: ; , y .${\displaystyle {\frac {IQ}{PI}}={\frac {FS}{D}}}$ ${\displaystyle {\frac {PQ}{PI}}={\frac {PF}{D}}}$${\displaystyle {\frac {RI}{PI}}={\frac {DF}{PF}}}$

Si HI es suficientemente pequeño como para poder tomarse como una línea recta, es un ángulo recto, y , de modo que .${\displaystyle \angle SIH}$${\displaystyle \angle RIH=\angle FIS}$${\displaystyle {\frac {HI}{RI}}={\frac {a}{IF}}}$

De ahí la fuerza sobre P debido al anillo .${\displaystyle \propto {\frac {IH\cdot IQ\cdot PQ}{PI^{3}}}={\frac {a\cdot DF\cdot FS\cdot PF}{IF\cdot PF\cdot D\cdot D}}={\frac {a\cdot DF\cdot FS}{IF\cdot D^{2}}}}$

Supongamos ahora en la Fig. 2 que otra partícula está fuera de la esfera en un punto p , a una distancia diferente d del centro de la esfera, con los puntos correspondientes marcados con letras minúsculas. Para facilitar la comparación, la construcción de P en la Fig. 1 también se muestra en la Fig. 2. Como antes, ph es menor que pt .

Genere un anillo con ancho ih y radio iq haciendo que el ángulo y el ángulo ligeramente mayor , de modo que la distancia PS esté subtendida por el mismo ángulo en I que pS en i. Lo mismo se aplica a H y h, respectivamente.${\displaystyle fiS=FIS}$${\displaystyle dhS=DHS}$

La fuerza total sobre p debido a este anillo es

${\displaystyle \propto {\frac {ih\cdot iq\cdot pq}{pi^{3}}}={\frac {a\cdot df\cdot fS}{if\cdot d^{2}}}}$

Claramente , , y .${\displaystyle fS=FS}$ ${\displaystyle if=IF}$${\displaystyle eS=ES}$

Newton afirma que DF y df pueden considerarse iguales en el límite, ya que los ángulos DPF y dpf "se desvanecen juntos". Nótese que los ángulos DPF y dpf no son iguales. Aunque DS y dS se vuelven iguales en el límite, esto no implica que la relación entre DF y df se vuelva igual a la unidad, cuando DF y df se aproximan a cero. En el caso finito, DF depende de D y df de d, por lo que no son iguales.

Dado que la relación entre DF y df en el límite es crucial, se requiere un análisis más detallado. A partir de los triángulos rectángulos semejantes, y , obtenemos . Resolviendo la ecuación cuadrática para DF, en el límite, cuando ES se acerca a FS, la raíz más pequeña, . De manera más simple, cuando DF se acerca a cero, en el límite el término puede ignorarse: lo que lleva al mismo resultado. Claramente, df tiene el mismo límite, lo que justifica la afirmación de Newton.${\textstyle {\frac {DF}{PF}}={\frac {ED}{ES}}}$${\displaystyle ED^{2}=(DF+FS)^{2}-ES^{2}}$${\displaystyle {\frac {\left(PF^{2}-ES^{2}\right)DF^{2}}{PF^{2}}}+2\cdot FS\cdot DF+FS^{2}-ES^{2}=0}$${\displaystyle DF=ES-FS}$${\displaystyle DF^{2}}$${\displaystyle 2\cdot FS\cdot DF+FS^{2}-ES^{2}=0}$

Comparando la fuerza del anillo HI girado alrededor de PS con la del anillo hi alrededor de pS, la relación de estas dos fuerzas es igual a .${\textstyle {\frac {d^{2}}{D^{2}}}}$

Dividiendo los arcos AT y Bt en anillos infinitesimales correspondientes, se deduce que la relación entre la fuerza debida al arco AT girado alrededor de PS y la de Bt girado alrededor de pS está en la misma relación, y de manera similar, la relación entre las fuerzas debidas al arco TB y la de tA, ambos girados, están en la misma relación.

Por lo tanto, la fuerza sobre una partícula a cualquier distancia D del centro de la esfera hueca es inversamente proporcional a , lo que demuestra la proposición.${\displaystyle D^{2}}$

Existe un análogo del teorema de capas en la relatividad general (RG).

La simetría esférica implica que la métrica tiene una geometría de Schwarzschild independiente del tiempo, incluso si una masa central está sufriendo un colapso gravitacional (Misner et al. 1973; véase el teorema de Birkhoff ). Por lo tanto, la métrica tiene forma

${\displaystyle ds^{2}=-(1-2M/r)\,dt^{2}+(1-2M/r)^{-1}\,dr^{2}+r^{2}\,d\Omega ^{2}}$

(usando unidades geometrizadas , donde ). Para (donde es el radio de alguna capa de masa), la masa actúa como una función delta en el origen. Para , las capas de masa pueden existir externamente, pero para que la métrica no sea singular en el origen, debe ser cero en la métrica. Esto reduce la métrica al espacio plano de Minkowski ; por lo tanto, las capas externas no tienen efecto gravitacional. ${\displaystyle G=c=1}$${\displaystyle r>R>0}$${\displaystyle R}$${\displaystyle r<R}$${\displaystyle M}$

Este resultado ilumina el colapso gravitacional que conduce a un agujero negro y su efecto sobre el movimiento de los rayos de luz y las partículas fuera y dentro del horizonte de eventos (Hartle 2003, capítulo 12).

Wikimedia Commons alberga una categoría multimedia sobre Teorema de capas .

• Teorema de Chasles (gravitación)
• Altura de la escala