Teodoro de Cirene

Teodoro de Cirene ( en griego Θεόδωρος ὁ Κυρηναῖος , translit.  Theódōros ho Kyrēnaîos ; fl. c. 450 a. C.) fue un matemático griego de la antigüedad . Los únicos relatos de primera mano que sobreviven sobre él se encuentran en tres de los diálogos de Platón : el Teeteto , el Sofista y el Estadista . En el primer diálogo, propone una construcción matemática ahora conocida como la Espiral de Teodoro .

Poco se sabe de la biografía de Teodoro más allá de lo que se puede inferir de los diálogos de Platón. Nació en la colonia de Cirene , en el norte de África , y aparentemente enseñó tanto allí como en Atenas . ^[1] Se queja de su vejez en el Teeteto , cuya dramática fecha de 399 a. C. sugiere que su período de florecimiento ocurrió a mediados del siglo V. El texto también lo asocia con el sofista Protágoras , con quien afirma haber estudiado antes de dedicarse a la geometría. ^[2] Una dudosa tradición repetida entre biógrafos antiguos como Diógenes Laercio ^[3] sostenía que Platón estudió más tarde con él en Cirene , Libia. ^[1] Este eminente matemático Teodoro fue, junto con Alcibíades y muchos otros compañeros de Sócrates (muchos de los cuales estarían asociados con los Treinta Tiranos ), acusado de distribuir los misterios en un simposio, según Plutarco , quien era sacerdote del templo de Delfos .

La obra de Teodoro es conocida a través de un único teorema, que se presenta en el contexto literario del Teeteto y del que se ha argumentado alternativamente que es históricamente exacto o ficticio. ^[1] En el texto, su alumno Teeteto le atribuye el teorema de que las raíces cuadradas de los números no cuadrados hasta el 17 son irracionales:

Teodoro estaba dibujando aquí algunas figuras para nosotros como ilustración de las raíces, mostrando que los cuadrados que contienen tres pies cuadrados y cinco pies cuadrados no son conmensurables en longitud con la unidad del pie, y así, seleccionando cada uno a su turno hasta el cuadrado que contiene diecisiete pies cuadrados y en ese se detuvo. ^[4]

El cuadrado que contiene dos unidades cuadradas no se menciona, tal vez porque ya se conocía la inconmensurabilidad de su lado con la unidad.) No se conoce el método de prueba de Teodoro. Ni siquiera se sabe si, en el pasaje citado, "hasta" (μέχρι) significa que se incluye diecisiete. Si se excluye diecisiete, entonces la prueba de Teodoro puede haberse basado simplemente en considerar si los números son pares o impares. De hecho, Hardy y Wright ^[5] y Knorr ^[6] sugieren pruebas que se basan en última instancia en el siguiente teorema: Si es soluble en números enteros , y es impar, entonces deben ser congruentes con 1 módulo 8 (ya que y pueden asumirse impares, por lo que sus cuadrados son congruentes con 1 módulo 8.${\displaystyle x^{2}=ny^{2}}$${\estilo de visualización n}$${\estilo de visualización n}$${\estilo de visualización x}$${\estilo de visualización y}$

Que no se puede probar la irracionalidad de la raíz cuadrada de 17 por consideraciones restringidas a la aritmética de los pares y los impares se ha demostrado en un sistema de aritmética de los pares y los impares en ^[7] y ^[8], pero es un problema abierto en un sistema de axiomas naturales más fuerte para la aritmética de los pares y los impares ^[9].

Una posibilidad sugerida anteriormente por Zeuthen ^[10] es que Teodoro aplicó el llamado algoritmo euclidiano , formulado en la Proposición X.2 de los Elementos como una prueba de inconmensurabilidad. En términos modernos, el teorema es que un número real con una expansión de fracción continua infinita es irracional. Las raíces cuadradas irracionales tienen expansiones periódicas . El período de la raíz cuadrada de 19 tiene una longitud de 6, que es mayor que el período de la raíz cuadrada de cualquier número más pequeño. El período de √17 tiene una longitud de uno (también la tiene √18; pero la irracionalidad de √18 se sigue de la de √2).

La llamada espiral de Teodoro está compuesta por triángulos rectángulos contiguos con longitudes de hipotenusa iguales a √2, √3, √4, …, √17; los triángulos adicionales hacen que el diagrama se superponga. Philip J. Davis interpoló los vértices de la espiral para obtener una curva continua. Analiza la historia de los intentos de determinar el método de Teodoro en su libro Spirals: From Theodorus to Chaos y hace breves referencias al asunto en su serie ficticia Thomas Gray .

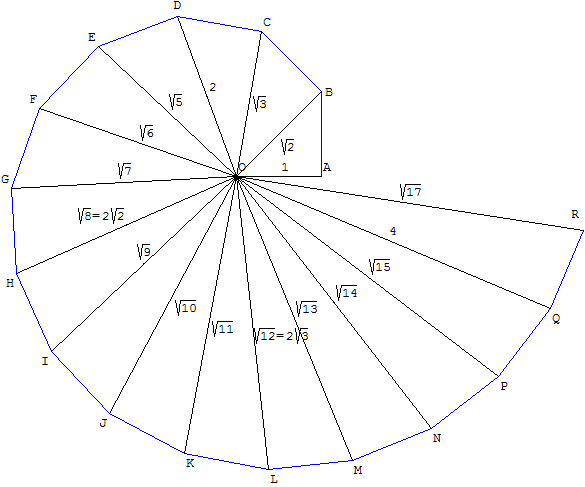
Que Teeteto estableció una teoría más general de los irracionales, según la cual las raíces cuadradas de los números no cuadrados son irracionales, se sugiere en el diálogo platónico homónimo, así como en el comentario y los escolios de los Elementos . ^[11]

• Cronología de los matemáticos griegos antiguos
• Lista de oradores en los diálogos de Platón
• Irracional cuadrático
• Wilbur Knorr

• Choike, James R. (1980). "Las pruebas de irracionalidad de Teodoro". The Two-Year College Mathematics Journal .
• Gow, James (1884). Breve historia de las matemáticas griegas. University Press. pág. 85.