Reflector Cassegrain

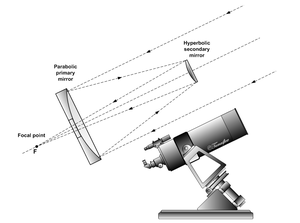
El reflector Cassegrain es una combinación de un espejo cóncavo primario y un espejo convexo secundario , que se utiliza a menudo en telescopios ópticos y antenas de radio . La característica principal es que el camino óptico se pliega sobre sí mismo, en relación con la abertura de entrada del espejo primario del sistema óptico. Este diseño coloca el punto focal en una ubicación conveniente detrás del espejo primario y el espejo secundario convexo agrega un efecto de telefoto creando una distancia focal mucho más larga en un sistema mecánicamente corto. ^[1]

En un Cassegrain simétrico, ambos espejos están alineados alrededor del eje óptico y el espejo primario generalmente contiene un orificio en el centro, lo que permite que la luz llegue a un ocular , una cámara o un sensor de imagen . Alternativamente, como en muchos radiotelescopios, el foco final puede estar frente al primario. En un Cassegrain asimétrico, el espejo o los espejos pueden estar inclinados para evitar el oscurecimiento del primario o para evitar la necesidad de un orificio en el espejo primario (o ambos).

La configuración clásica de Cassegrain utiliza un reflector parabólico como primario mientras que el espejo secundario es hiperbólico . ^[2] Las variantes modernas pueden tener un primario hiperbólico para un mayor rendimiento (por ejemplo, el diseño Ritchey-Chrétien ); y uno o ambos espejos pueden ser esféricos o elípticos para facilitar la fabricación.

El reflector Cassegrain recibe su nombre de un diseño de telescopio reflector publicado en el Journal des sçavans del 25 de abril de 1672, que se ha atribuido a Laurent Cassegrain . ^[3] Se han encontrado diseños similares que utilizan espejos secundarios convexos en los escritos de Bonaventura Cavalieri de 1632 que describen espejos en llamas ^{[4] [5]} y en los escritos de Marin Mersenne de 1636 que describen diseños de telescopios. ^{[6] Los intentos de} James Gregory de 1662 de crear un telescopio reflector incluyeron una configuración Cassegrain, a juzgar por un espejo secundario convexo encontrado entre sus experimentos. ^[7]

El diseño Cassegrain también se utiliza en sistemas catadióptricos .

El Cassegrain "clásico" tiene un espejo primario parabólico y un espejo secundario hiperbólico que refleja la luz hacia abajo a través de un orificio en el primario. Al plegar la óptica, se obtiene un diseño compacto. En telescopios más pequeños y lentes de cámara, el secundario suele estar montado sobre una placa de vidrio ópticamente plana y ópticamente transparente que cierra el tubo del telescopio. Este soporte elimina los efectos de difracción en "forma de estrella" causados ​​por una araña de soporte de paletas rectas. El tubo cerrado se mantiene limpio y el primario está protegido, a costa de cierta pérdida de poder de captación de luz.

Utiliza las propiedades especiales de los reflectores parabólicos e hiperbólicos. Un reflector parabólico cóncavo reflejará todos los rayos de luz entrantes paralelos a su eje de simetría hacia un único punto, el foco. Un reflector hiperbólico convexo tiene dos focos y reflejará todos los rayos de luz dirigidos a uno de sus dos focos hacia su otro foco. Los espejos de este tipo de telescopio están diseñados y posicionados de manera que compartan un foco y de manera que el segundo foco del espejo hiperbólico esté en el mismo punto en el que se va a observar la imagen, normalmente justo fuera del ocular.

En la mayoría de los sistemas Cassegrain, el espejo secundario bloquea una parte central de la apertura. Esta apertura de entrada en forma de anillo reduce significativamente una parte de la función de transferencia de modulación (MTF) en un rango de frecuencias espaciales bajas, en comparación con un diseño de apertura completa, como un refractor o un Cassegrain desplazado. ^[8] Esta muesca de MTF tiene el efecto de reducir el contraste de la imagen cuando se capturan imágenes de características amplias. Además, el soporte para el secundario (la araña) puede introducir picos de difracción en las imágenes.

Los radios de curvatura de los espejos primario y secundario, respectivamente, en la configuración clásica son

${\displaystyle R_{1}=-{\frac {2DF}{FB}}=-{\frac {2F}{M}}}$

y

${\displaystyle R_{2}=-{\frac {2DB}{FBD}}=-{\frac {2B}{M-1}}}$

dónde

• ${\estilo de visualización F}$es la distancia focal efectiva del sistema,
• ${\estilo de visualización B}$es la distancia focal posterior (la distancia desde el secundario hasta el foco),
• ${\estilo de visualización D}$es la distancia entre los dos espejos y
• ${\displaystyle M=(FB)/D}$es el aumento secundario.

Si, en lugar de y , las cantidades conocidas son la distancia focal del espejo primario, , y la distancia al foco detrás del espejo primario, , entonces y .${\estilo de visualización B}$${\estilo de visualización D}$$estilo de visualización f_{1}}$${\estilo de visualización b}$${\displaystyle D=f_{1}(F-b)/(F+f_{1})}$${\displaystyle B=D+b}$

La constante cónica del espejo primario es la de una parábola, . Gracias a ello , el espejo primario no introduce ninguna aberración esférica . Sin embargo, el espejo secundario tiene forma hiperbólica, con un foco que coincide con el del espejo primario y el otro foco que se encuentra en la distancia focal posterior . Por lo tanto, el Cassegrain clásico tiene un foco ideal para el rayo principal (el diagrama del punto central es un punto). Tenemos,${\displaystyle K_{1}=-1}$${\displaystyle B}$

${\displaystyle K_{2}=-1-\alpha -{\sqrt {\alpha (\alpha +2)}}}$,

dónde

${\displaystyle \alpha ={\frac {1}{2}}\left[{\frac {4DBM}{(F+BM-DM)(F-B-D)}}\right]^{2}}$.

En realidad, como las constantes cónicas no deberían depender de la escala, las fórmulas para ambos pueden simplificarse en gran medida y presentarse solo como funciones del aumento secundario. Finalmente,${\displaystyle \alpha }$${\displaystyle K_{2}}$

${\displaystyle \alpha ={\frac {8M^{2}}{(M^{2}-1)^{2}}}}$

y

${\displaystyle K_{2}=-1-{\frac {4M}{(M-1)^{2}}}=-\left({\frac {M+1}{M-1}}\right)^{2}}$.

El Ritchey-Chrétien es un reflector Cassegrain especializado que tiene dos espejos hiperbólicos (en lugar de un espejo primario parabólico). No presenta coma ni aberración esférica en un plano focal plano, lo que lo hace muy adecuado para observaciones fotográficas y de campo amplio. Fue inventado por George Willis Ritchey y Henri Chrétien a principios de la década de 1910. Este diseño es muy común en los grandes telescopios de investigación profesional, incluidos el telescopio espacial Hubble , los telescopios Keck y el Very Large Telescope (VLT); también se encuentra en telescopios amateur de alta calidad.

El diseño del telescopio Cassegrain de Dall-Kirkham fue creado por Horace Dall en 1928 y adoptó el nombre en un artículo publicado en Scientific American en 1930 tras una discusión entre el astrónomo aficionado Allan Kirkham y Albert G. Ingalls, el editor de astronomía de la revista en ese momento. Utiliza un espejo primario elíptico cóncavo y un secundario esférico convexo . Si bien este sistema es más fácil de pulir que un sistema Cassegrain o Ritchey-Chretien clásico, la coma fuera del eje es significativamente peor, por lo que la imagen se degrada rápidamente fuera del eje. Debido a que esto es menos perceptible en relaciones focales más largas , los Dall-Kirkham rara vez son más rápidos que f/15.

Una variante inusual del Cassegrain es el telescopio Schiefspiegler (de "reflector sesgado" u "oblicuo"; también conocido como "telescopio Kutter" en honor a su inventor, Anton Kutter ^[9] ), que utiliza espejos inclinados para evitar que el espejo secundario proyecte una sombra sobre el primario. Sin embargo, si bien elimina los patrones de difracción, esto conduce a varias otras aberraciones que deben corregirse.

Se utilizan varias configuraciones diferentes fuera del eje para las antenas de radio. ^[10]

Otro diseño sin obstrucciones y fuera del eje y una variante del Cassegrain es el reflector " Yolo " inventado por Arthur Leonard. Este diseño utiliza un reflector primario esférico o parabólico y un reflector secundario esférico deformado mecánicamente para corregir el astigmatismo inducido fuera del eje. Cuando se configura correctamente, el Yolo puede proporcionar vistas sin obstrucciones de objetos planetarios y objetivos de campo no amplio, sin pérdida de contraste o calidad de imagen causada por la aberración esférica. La falta de obstrucciones también elimina la difracción asociada con la astrofotografía con reflectores Cassegrain y Newtonianos.

Los Cassegrains catadióptricos utilizan dos espejos, a menudo con un espejo primario esférico para reducir costos, combinado con elementos correctores refractivos para corregir las aberraciones resultantes.

El Schmidt-Cassegrain se desarrolló a partir de la cámara Schmidt de campo amplio , aunque la configuración Cassegrain le da un campo de visión mucho más estrecho. El primer elemento óptico es una placa correctora Schmidt . La placa se forma colocando un vacío en un lado y puliendo la corrección exacta requerida para corregir la aberración esférica causada por el espejo primario esférico. Los Schmidt-Cassegrain son populares entre los astrónomos aficionados. Una de las primeras cámaras Schmidt-Cassegrain fue patentada en 1946 por el artista, arquitecto y físico Roger Hayward ^[11] , con el soporte de película colocado fuera del telescopio.

El Maksutov-Cassegrain es una variante del telescopio Maksutov que lleva el nombre del óptico y astrónomo soviético / ucraniano Dmitri Dmitrievich Maksutov . Comienza con una lente correctora ópticamente transparente que es una sección de una esfera hueca. Tiene un espejo primario esférico y un espejo secundario esférico que suele ser una sección reflejada de la lente correctora.

En el telescopio Argunov-Cassegrain, toda la óptica es esférica y el clásico espejo secundario Cassegrain se sustituye por un corrector de subapertura que consta de tres elementos de lentes espaciados por aire. El elemento más alejado del espejo primario es un espejo Mangin , que actúa como espejo secundario.

El Klevtsov-Cassegrain, al igual que el Argunov-Cassegrain, utiliza un corrector de sub-apertura que consiste en una pequeña lente de menisco y un espejo Mangin como su "espejo secundario". ^[12]

Los diseños Cassegrain también se utilizan en antenas de estaciones terrestres de telecomunicaciones por satélite y radiotelescopios , cuyo tamaño varía de 2,4 metros a 70 metros. El subreflector ubicado en el centro sirve para enfocar las señales de radiofrecuencia de manera similar a los telescopios ópticos.

Un ejemplo de antena de radio Cassegrain es la antena parabólica de 70 metros del complejo de antenas Goldstone del JPL . En esta antena, el foco final se encuentra delante del primario, en la parte superior del pedestal que sobresale del espejo.

• Sistema catadióptrico
• Celestron (Schmidt-Cassegrains, Maksutov Cassegrains)
• Lista de tipos de telescopios
• Instrumentos Meade (Schmidt-Cassegrains, Maksutov Cassegrains)
• Questar (Maksutov Cassegrains)
• Telescopio refractor
• Vixen (Cassegrains, Klevtsov-Cassegrain)

• Medios relacionados con los telescopios Cassegrain en Wikimedia Commons
• Modelado de antenas reflectoras Cassegrain en MATLAB en Wayback Machine (archivado el 3 de marzo de 2024)