Formato del sensor de imagen
En fotografía digital, el formato del sensor de imagen es la forma y el tamaño del sensor de imagen .
El formato del sensor de imagen de una cámara digital determina el ángulo de visión de un objetivo concreto cuando se utiliza con un sensor concreto. Dado que los sensores de imagen de muchas cámaras digitales son más pequeños que el área de imagen de 24 mm × 36 mm de las cámaras de fotograma completo de 35 mm , un objetivo de una determinada distancia focal proporciona un campo de visión más estrecho en dichas cámaras.
El tamaño del sensor suele expresarse en formato óptico en pulgadas. También se utilizan otras medidas; consulte la tabla de formatos y tamaños de sensores que aparece a continuación.
Las lentes fabricadas para cámaras de película de 35 mm pueden montarse bien en los cuerpos digitales, pero el círculo de imagen más grande de la lente del sistema de 35 mm permite que entre luz no deseada en el cuerpo de la cámara, y el tamaño más pequeño del sensor de imagen en comparación con el formato de película de 35 mm da como resultado un recorte de la imagen. Este último efecto se conoce como recorte del campo de visión. La relación de tamaño del formato (en relación con el formato de película de 35 mm) se conoce como factor de recorte del campo de visión, factor de recorte, factor de lente, factor de conversión de longitud focal, multiplicador de longitud focal o multiplicador de lente.
Tamaño del sensor y profundidad de campo
Se analizan tres posibles comparaciones de profundidad de campo entre formatos, aplicando las fórmulas derivadas del artículo sobre profundidad de campo . Las profundidades de campo de las tres cámaras pueden ser iguales o diferentes en cualquier orden, dependiendo de lo que se mantenga constante en la comparación.
Considerando una imagen con la misma distancia del sujeto y ángulo de visión para dos formatos diferentes:
Por lo tanto, los grados de libertad son inversamente proporcionales a los diámetros de apertura absolutos y .
Si se utiliza el mismo diámetro de apertura absoluta para ambos formatos con el criterio de "misma imagen" (igual ángulo de visión, ampliada al mismo tamaño final), se obtiene la misma profundidad de campo. Esto equivale a ajustar el número f de forma inversamente proporcional al factor de recorte : un número f menor para sensores más pequeños (esto también significa que, al mantener fija la velocidad de obturación, la exposición cambia mediante el ajuste del número f necesario para igualar la profundidad de campo. Pero el área de apertura se mantiene constante, por lo que los sensores de todos los tamaños reciben la misma cantidad total de energía luminosa del sujeto. El sensor más pequeño funciona entonces con un ajuste ISO más bajo , por el cuadrado del factor de recorte). Esta condición de igual campo de visión, igual profundidad de campo, igual diámetro de apertura y igual tiempo de exposición se conoce como "equivalencia". [1]
Y, podríamos comparar la profundidad de campo de los sensores que reciben la misma exposición fotométrica (el número f es fijo en lugar del diámetro de apertura); los sensores funcionan con la misma configuración ISO en ese caso, pero el sensor más pequeño recibe menos luz total, por la relación de área. La relación de profundidades de campo es entonces
donde y son las dimensiones características del formato, y por tanto es el factor de recorte relativo entre los sensores. Es este resultado el que da lugar a la opinión común de que los sensores pequeños ofrecen una mayor profundidad de campo que los grandes.
Una alternativa es considerar la profundidad de campo proporcionada por la misma lente en combinación con sensores de diferentes tamaños (cambiando el ángulo de visión). El cambio en la profundidad de campo se produce por la necesidad de un grado diferente de ampliación para lograr el mismo tamaño de imagen final. En este caso, la relación de profundidades de campo se convierte en
- .
En la práctica, si se aplica una lente con una distancia focal fija y una apertura fija y hecha para un círculo de imagen para cumplir con los requisitos de un sensor grande, se debe adaptar, sin cambiar sus propiedades físicas, a tamaños de sensor más pequeños, ni la profundidad de campo ni la captación de luz cambiarán.
Tamaño del sensor, ruido y rango dinámico
Si se descuenta la falta de uniformidad de la respuesta a la foto (PRNU) y la variación del ruido oscuro, que no dependen intrínsecamente del tamaño del sensor, los ruidos en un sensor de imagen son el ruido de disparo, el ruido de lectura y el ruido oscuro. La relación señal/ruido general de un sensor (SNR), expresada como electrones de señal en relación con el ruido rms en electrones, observados a la escala de un solo píxel, suponiendo que el ruido de disparo se debe a la distribución de Poisson de los electrones de señal y los electrones oscuros, es
donde es el flujo de fotones incidentes (fotones por segundo en el área de un píxel), es la eficiencia cuántica , es el tiempo de exposición, es la corriente oscura del píxel en electrones por segundo y es el ruido de lectura del píxel en electrones rms. [2]
Cada uno de estos ruidos tiene una dependencia diferente del tamaño del sensor.
Exposición y flujo de fotones
El ruido del sensor de imagen se puede comparar entre formatos para un flujo de fotones fijo determinado por área de píxel (la P en las fórmulas); este análisis es útil para un número fijo de píxeles con un área de píxeles proporcional al área del sensor y un diámetro de apertura absoluto fijo para una situación de imagen fija en términos de profundidad de campo, límite de difracción en el sujeto, etc. O se puede comparar para una iluminancia de plano focal fija, correspondiente a un número f fijo , en cuyo caso P es proporcional al área de píxeles, independientemente del área del sensor. Las fórmulas anteriores y siguientes se pueden evaluar para cualquiera de los casos.
Ruido de disparo
En la ecuación anterior, la relación señal-ruido (SNR) del ruido de disparo se expresa mediante
- .
Aparte de la eficiencia cuántica, depende del flujo de fotones incidentes y del tiempo de exposición, que es equivalente a la exposición y al área del sensor; ya que la exposición es el tiempo de integración multiplicado por la iluminancia del plano de la imagen , y la iluminancia es el flujo luminoso por unidad de área. Por lo tanto, para exposiciones iguales, las relaciones señal/ruido de dos sensores de tamaño diferente con la misma eficiencia cuántica y cantidad de píxeles serán (para un tamaño de imagen final determinado) proporcionales a la raíz cuadrada del área del sensor (o al factor de escala lineal del sensor). Si la exposición está limitada por la necesidad de lograr cierta profundidad de campo requerida (con la misma velocidad de obturación), las exposiciones estarán en relación inversa con el área del sensor, lo que produce el interesante resultado de que si la profundidad de campo es una restricción, el ruido de la imagen tomada no depende del área del sensor. Para lentes con números f idénticos, la relación señal/ruido aumenta como la raíz cuadrada del área de píxeles, o linealmente con el paso de píxeles. Como los números f típicos para lentes para teléfonos celulares y DSLR están en el mismo rangof /1,5–2Es interesante comparar el rendimiento de las cámaras con sensores pequeños y grandes. Una buena cámara de teléfono móvil con un tamaño de píxel típico de 1,1 μm (Samsung A8) tendría una relación señal/ruido (SNR) aproximadamente tres veces peor que una cámara con lentes intercambiables de 3,7 μm (Panasonic G85) debido al ruido de disparo y cinco veces peor que una cámara de fotograma completo de 6 μm (Sony A7 III). Si se tiene en cuenta el rango dinámico, la diferencia es aún más evidente. Por ello, la tendencia de aumentar el número de "megapíxeles" en las cámaras de los teléfonos móviles durante los últimos 10 años se debió más a una estrategia de marketing para vender "más megapíxeles" que a intentos de mejorar la calidad de la imagen.
Leer ruido
El ruido de lectura es el total de todos los ruidos electrónicos en la cadena de conversión de los píxeles en la matriz del sensor. Para compararlo con el ruido de fotones, debe remitirse a su equivalente en fotoelectrones, lo que requiere la división del ruido medido en voltios por la ganancia de conversión del píxel. Esto se da, para un sensor de píxeles activo , por el voltaje en la entrada (puerta) del transistor de lectura dividido por la carga que genera ese voltaje, . Esta es la inversa de la capacitancia de la compuerta del transistor de lectura (y la difusión flotante adjunta) ya que la capacitancia . [3] Por lo tanto .
En general, para una estructura plana como un píxel, la capacitancia es proporcional al área, por lo tanto, el ruido de lectura se reduce con el área del sensor, siempre que el área del píxel se escale con el área del sensor, y ese escalamiento se realice escalando uniformemente el píxel.
Teniendo en cuenta la relación señal/ruido debida al ruido de lectura en una exposición determinada, la señal se escalará como el área del sensor junto con el ruido de lectura y, por lo tanto, la relación señal/ruido del ruido de lectura no se verá afectada por el área del sensor. En una situación con limitaciones de profundidad de campo, la exposición del sensor más grande se reducirá en proporción al área del sensor y, por lo tanto, la relación señal/ruido del ruido de lectura también se reducirá.
Ruido oscuro
La corriente oscura contribuye con dos tipos de ruido: el desplazamiento oscuro, que solo está parcialmente correlacionado entre píxeles, y el ruido de disparo asociado con el desplazamiento oscuro, que no está correlacionado entre píxeles. Solo el componente de ruido de disparo Dt está incluido en la fórmula anterior, ya que la parte no correlacionada del desplazamiento oscuro es difícil de predecir y la parte correlacionada o media es relativamente fácil de restar. La corriente oscura media contiene contribuciones proporcionales tanto al área como a la dimensión lineal del fotodiodo, con proporciones relativas y factores de escala que dependen del diseño del fotodiodo. [4] Por lo tanto, en general, se puede esperar que el ruido oscuro de un sensor aumente a medida que aumenta el tamaño del sensor. Sin embargo, en la mayoría de los sensores, la corriente oscura de píxel media a temperaturas normales es pequeña, inferior a 50 e- por segundo, [5] por lo que para tiempos de exposición fotográfica típicos, la corriente oscura y sus ruidos asociados pueden descartarse. Sin embargo, en tiempos de exposición muy largos, puede ser un factor limitante. Incluso con tiempos de exposición cortos o medios, pueden aparecer algunos valores atípicos en la distribución de la corriente oscura como "píxeles calientes". Normalmente, para las aplicaciones de astrofotografía, los sensores se enfrían para reducir la corriente oscura en situaciones en las que las exposiciones pueden medirse en varios cientos de segundos.
Rango dinámico
El rango dinámico es la relación entre la señal más grande y la más pequeña que se puede registrar, siendo la más pequeña la que se define normalmente como el "ruido de fondo". En la literatura sobre sensores de imagen, el ruido de fondo se toma como el ruido de lectura, por lo que [6] (tenga en cuenta que el ruido de lectura es la misma cantidad a la que se hace referencia en el cálculo de la relación señal-ruido [2] ).
Tamaño del sensor y difracción
La resolución de todos los sistemas ópticos está limitada por la difracción . Una forma de considerar el efecto que tiene la difracción en las cámaras que utilizan sensores de diferentes tamaños es considerar la función de transferencia de modulación (MTF). La difracción es uno de los factores que contribuyen a la MTF general del sistema. Otros factores son típicamente las MTF de la lente, el filtro anti-aliasing y la ventana de muestreo del sensor. [7] La frecuencia de corte espacial debido a la difracción a través de una apertura de lente es
donde λ es la longitud de onda de la luz que pasa a través del sistema y N es el número f de la lente. Si esa apertura es circular, como lo son (aproximadamente) la mayoría de las aperturas fotográficas, entonces la MTF viene dada por
para y para [8] Por lo tanto, el factor basado en difracción del sistema MTF se escalará de acuerdo con y a su vez de acuerdo con (para la misma longitud de onda de luz).
Al considerar el efecto del tamaño del sensor y su efecto en la imagen final, se debe tener en cuenta la diferente ampliación necesaria para obtener una imagen del mismo tamaño para su visualización, lo que da como resultado un factor de escala adicional de donde es el factor de recorte relativo, lo que hace que el factor de escala general sea . Teniendo en cuenta los tres casos anteriores:
Para las condiciones de "la misma imagen", el mismo ángulo de visión, la distancia del sujeto y la profundidad de campo, los números f están en la relación , por lo que el factor de escala para la MTF de difracción es 1, lo que lleva a la conclusión de que la MTF de difracción a una profundidad de campo dada es independiente del tamaño del sensor.
En las condiciones de "misma exposición fotométrica" y "misma lente", el número f no cambia y, por lo tanto, el corte espacial y el MTF resultante en el sensor no cambian, dejando el MTF en la imagen vista para escalarse como la ampliación, o inversamente como el factor de recorte.
Formato del sensor y tamaño de la lente
Se podría esperar que las lentes apropiadas para una variedad de tamaños de sensores pudieran producirse simplemente escalando los mismos diseños en proporción al factor de recorte. [9] Tal ejercicio produciría en teoría una lente con el mismo número f y ángulo de visión, con un tamaño proporcional al factor de recorte del sensor. En la práctica, el escalamiento simple de los diseños de lentes no siempre es alcanzable, debido a factores como la no escalabilidad de la tolerancia de fabricación , la integridad estructural de las lentes de vidrio de diferentes tamaños y las técnicas y costos de fabricación disponibles. Además, para mantener la misma cantidad absoluta de información en una imagen (que se puede medir como el producto espacio-ancho de banda [10] ), la lente para un sensor más pequeño requiere un mayor poder de resolución. Nasse analiza el desarrollo de la lente " Tessar " [11] y muestra su transformación de unaf /6,3Lente para cámaras de placas que utilizan la configuración original de tres grupos hasta unaf /2,8Óptica de cuatro elementos de 5,2 mm con ocho superficies extremadamente asféricas, económica de fabricar gracias a su pequeño tamaño. Su rendimiento es "mejor que el de los mejores objetivos de 35 mm, pero sólo para una imagen muy pequeña".
En resumen, a medida que se reduce el tamaño del sensor, los diseños de los objetivos que lo acompañan cambiarán, a menudo de forma bastante radical, para aprovechar las técnicas de fabricación que se han hecho disponibles gracias a la reducción del tamaño. La funcionalidad de estos objetivos también puede aprovechar estas ventajas, y se hacen posibles rangos de zoom extremos. Estos objetivos suelen ser muy grandes en relación con el tamaño del sensor, pero con un sensor pequeño se pueden colocar en un paquete compacto.
Un cuerpo pequeño significa una lente pequeña y un sensor pequeño, por lo que para mantener los teléfonos inteligentes delgados y livianos, los fabricantes de teléfonos inteligentes usan un sensor diminuto, generalmente más pequeño que el 1/2.3" que se usa en la mayoría de las cámaras bridge . En un momento, solo el Nokia 808 PureView usaba un sensor de 1/1.2", casi tres veces el tamaño de un sensor de 1/2.3". Los sensores más grandes tienen la ventaja de una mejor calidad de imagen, pero con las mejoras en la tecnología de sensores, los sensores más pequeños pueden lograr las hazañas de los sensores más grandes anteriores. Estas mejoras en la tecnología de sensores permiten a los fabricantes de teléfonos inteligentes usar sensores de imagen tan pequeños como 1/4" sin sacrificar demasiado la calidad de imagen en comparación con las cámaras compactas económicas. [12]
Área activa del sensor
Para calcular el ángulo de visión de la cámara se debe utilizar el tamaño del área activa del sensor. El área activa del sensor implica un área del sensor en la que se forma la imagen en un modo dado de la cámara. El área activa puede ser más pequeña que el sensor de imagen y el área activa puede diferir en diferentes modos de funcionamiento de la misma cámara. El tamaño del área activa depende de la relación de aspecto del sensor y de la relación de aspecto de la imagen de salida de la cámara. El tamaño del área activa puede depender del número de píxeles en un modo dado de la cámara. El tamaño del área activa y la distancia focal del objetivo determinan los ángulos de visión. [13]
Tamaño del sensor y efectos de sombreado
Los sensores de imagen semiconductores pueden sufrir efectos de sombreado en grandes aperturas y en la periferia del campo de imagen, debido a la geometría del cono de luz proyectado desde la pupila de salida de la lente a un punto, o píxel, en la superficie del sensor. Los efectos son discutidos en detalle por Catrysse y Wandell. [14] En el contexto de esta discusión, el resultado más importante de lo anterior es que para asegurar una transferencia completa de energía de luz entre dos sistemas ópticos acoplados, como la pupila de salida de la lente al fotorreceptor de un píxel, la extensión geométrica (también conocida como etendue o flujo de luz) del sistema de lente objetivo / píxel debe ser menor o igual que la extensión geométrica del sistema de microlente / fotorreceptor. La extensión geométrica del sistema de lente objetivo / píxel está dada por donde w píxel es el ancho del píxel y ( f / #) objetivo es el número f de la lente objetivo. La extensión geométrica del sistema microlente/fotorreceptor está dada por donde w fotorreceptor es el ancho del fotorreceptor y ( f /#) microlente es el número f de la microlente.
Para evitar el sombreado, por lo tanto
Si w fotorreceptor / w píxel = ff , el factor de relleno lineal de la lente, entonces la condición se convierte en
Por lo tanto, si se quiere evitar el sombreado, el número f de la microlente debe ser menor que el número f de la lente de captura en al menos un factor igual al factor de relleno lineal del píxel. El número f de la microlente está determinado en última instancia por el ancho del píxel y su altura sobre el silicio, que determina su longitud focal. A su vez, esto está determinado por la altura de las capas de metalización, también conocida como "altura de pila". Para una altura de pila dada, el número f de las microlentes aumentará a medida que se reduzca el tamaño del píxel y, por lo tanto, el número f de la lente objetivo en el que se produce el sombreado tenderá a aumentar. [a]
Para mantener el número de píxeles, los sensores más pequeños tienden a tener píxeles más pequeños, mientras que al mismo tiempo se requieren números f de lente objetivo más pequeños para maximizar la cantidad de luz proyectada en el sensor. Para combatir el efecto discutido anteriormente, los píxeles de formato más pequeño incluyen características de diseño de ingeniería para permitir la reducción del número f de sus microlentes. Estas pueden incluir diseños de píxeles simplificados que requieren menos metalización, "conductos de luz" construidos dentro del píxel para acercar su superficie aparente a la microlente e " iluminación del lado posterior " en la que la oblea se adelgaza para exponer la parte trasera de los fotodetectores y la capa de microlentes se coloca directamente sobre esa superficie, en lugar de la parte frontal con sus capas de cableado. [b]
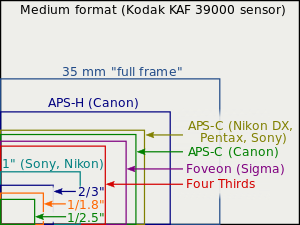
Formatos comunes de sensores de imagen
Para cámaras con lentes intercambiables
Algunas DSLR, SLT y cámaras sin espejo profesionales utilizan sensores de fotograma completo , equivalentes al tamaño de un fotograma de una película de 35 mm.
La mayoría de las DSLR, SLT y cámaras sin espejo para el consumidor utilizan sensores relativamente grandes, ya sea un poco más pequeños que el tamaño de un fotograma de una película APS -C, con un factor de recorte de 1,5 a 1,6; o un 30 % más pequeños que eso, con un factor de recorte de 2,0 (este es el sistema Cuatro Tercios , adoptado por Olympus y Panasonic ).
En noviembre de 2013 [update], solo había un modelo sin espejo equipado con un sensor muy pequeño, más típico de las cámaras compactas: la Pentax Q7 , con un sensor de 1/1,7" (factor de recorte de 4,55). Véase la sección Sensores que equipan las cámaras digitales compactas y los teléfonos con cámara más abajo.
En marketing se utilizan muchos términos diferentes para describir los formatos de sensores DSLR/SLT/sin espejo, incluidos los siguientes:
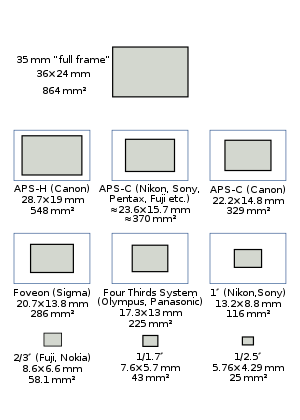
- Formato SLR digital de fotograma completo con área de 860 mm2 , con dimensiones de sensor casi iguales a las de la película de 35 mm (36×24 mm) de Pentax , Panasonic , Leica , Nikon , Canon , Sony y Sigma .
- Formato estándar APS-C de área 370 mm2 de Nikon , Pentax , Sony , Fujifilm , Sigma (factor de recorte 1,5) (sin embargo, la película APS-C real es más grande).
- Formato más pequeño APS-C de 330 mm y 2 áreas de Canon (factor de recorte 1,6)
- Formato Micro Four Thirds System de 225 mm de área 2 de Panasonic, Olympus, Black Magic y Polaroid (factor de recorte 2.0)
Los tamaños de sensores obsoletos y fuera de producción incluyen:
- Sensor Leica M8 y M8.2 de 548 mm2 de área (factor de recorte 1,33). Los sensores actuales de la serie M son de formato completo (factor de recorte 1,0).
- Área de 548 mm2 Formato APS-H de Canon para DSLR de nivel profesional de alta velocidad (factor de recorte 1,3). Los sensores actuales de las series 1D/5D son efectivamente de fotograma completo (factor de recorte 1,0).
- Formato APS-H de 548 mm y 2 áreas para la cámara sin espejo de gama alta SD Quattro H de Sigma (factor de recorte 1,35)
- Formato APS-C de área de 370 mm2, factor de recorte 1,5 de Epson , Samsung NX , Konica Minolta .
- Formato Foveon X3 de 286 mm2 de área utilizado en las DSLR de la serie SD de Sigma y las cámaras sin espejo de la serie DP (factor de recorte 1,7). Los modelos posteriores, como la SD1 , la DP2 Merrill y la mayoría de las cámaras de la serie Quattro, utilizan un sensor Foveon con factor de recorte 1,5; la cámara sin espejo Quattro H, aún más reciente, utiliza un sensor Foveon APS-H con un factor de recorte 1,35.
- Formato del sistema Cuatro Tercios de Olympus con área de 225 mm2 ( factor de recorte 2,0)
- Área de 116 mm 2 Formato Nikon CX de 1" utilizado en la serie Nikon 1 [17] y la serie mini-NX de Samsung (factor de recorte 2,7)
- Pentax Q7 de 43 mm2 de área 1/1,7" (factor de recorte 4,55)
- Área de 30 mm2 , 1/2,3" Pentax Q original (factor de recorte de 5,6). Las cámaras de la serie Q actuales tienen un factor de recorte de 4,55.
Cuando se introdujeron por primera vez los sensores de fotograma completo , los costes de producción podían superar veinte veces el coste de un sensor APS-C. Sólo se pueden producir veinte sensores de fotograma completo en una oblea de silicio de 20 cm (8 pulgadas) , en la que cabrían 100 o más sensores APS-C, y hay una reducción significativa en el rendimiento debido a la gran superficie para contaminantes por componente. Además, la fabricación de sensores de fotograma completo requería originalmente tres exposiciones independientes durante cada paso del proceso de fotolitografía , lo que requiere máscaras independientes y pasos de control de calidad. Canon seleccionó el tamaño intermedio APS-H , ya que en ese momento era el más grande que se podía modelar con una sola máscara, lo que ayudaba a controlar los costes de producción y gestionar los rendimientos. [18] Los equipos de fotolitografía más nuevos permiten ahora exposiciones de una sola pasada para sensores de fotograma completo, aunque otras limitaciones de producción relacionadas con el tamaño siguen siendo prácticamente las mismas.
Debido a las limitaciones en constante cambio de la fabricación y el procesamiento de semiconductores , y debido a que los fabricantes de cámaras a menudo obtienen sensores de fundiciones de terceros , es común que las dimensiones del sensor varíen ligeramente dentro del mismo formato nominal. Por ejemplo, los sensores nominalmente de fotograma completo de las cámaras Nikon D3 y D700 en realidad miden 36 × 23,9 mm, ligeramente más pequeños que un fotograma de 36 × 24 mm de película de 35 mm. Como otro ejemplo, el sensor de la Pentax K200D (fabricado por Sony ) mide 23,5 × 15,7 mm, mientras que el sensor de la contemporánea K20D (fabricado por Samsung ) mide 23,4 × 15,6 mm.
La mayoría de estos formatos de sensores de imagen se aproximan a la relación de aspecto 3:2 de la película de 35 mm. Una vez más, el sistema Cuatro Tercios es una notable excepción, con una relación de aspecto de 4:3, como la que se observa en la mayoría de las cámaras digitales compactas (ver a continuación).
Sensores más pequeños
La mayoría de los sensores están diseñados para teléfonos con cámara, cámaras digitales compactas y cámaras bridge. La mayoría de los sensores de imagen que equipan las cámaras compactas tienen una relación de aspecto de 4:3. Esta relación de aspecto coincide con la de las resoluciones de pantalla SVGA , XGA y SXGA populares en la época de las primeras cámaras digitales, lo que permite visualizar imágenes en monitores comunes sin recortarlas.
A partir de diciembre de 2010, [update]la mayoría de las cámaras digitales compactas utilizaban sensores pequeños de 1/2,3". Entre estas cámaras se incluyen la Canon Powershot SX230 IS, la Fuji Finepix Z90 y la Nikon Coolpix S9100. Algunas cámaras digitales más antiguas (principalmente de 2005 a 2010) utilizaban sensores aún más pequeños de 1/2,5": entre ellas, la Panasonic Lumix DMC-FS62, la Canon Powershot SX120 IS, la Sony Cyber-shot DSC-S700 y la Casio Exilim EX-Z80.
A partir de 2018, las cámaras compactas de gama alta que utilizan sensores de una pulgada que tienen casi cuatro veces el área de los que equipan las compactas comunes incluyen la serie G de Canon PowerShot (G3 X a G9 X), la serie Sony DSC RX100, la Panasonic Lumix TZ100 y la Panasonic DMC-LX15. Canon tiene un sensor APS-C en su modelo superior, la PowerShot G1 X Mark III.

Por último, Sony tiene en su gama las cámaras DSC-RX1 y DSC-RX1R, que tienen un sensor de fotograma completo que normalmente sólo se utiliza en DSLR, SLT y MILC profesionales.
Debido a las limitaciones de tamaño de los objetivos con zoom potentes, la mayoría de las cámaras bridge actuales tienen sensores de 1/2,3", tan pequeños como los que se utilizan en las cámaras más compactas comunes. Como los tamaños de los lentes son proporcionales al tamaño del sensor de imagen, los sensores más pequeños permiten grandes cantidades de zoom con lentes de tamaño moderado. En 2011, la Fujifilm X-S1 de gama alta estaba equipada con un sensor de 2/3" mucho más grande. En 2013-2014, tanto Sony ( Cyber-shot DSC-RX10 ) como Panasonic ( Lumix DMC-FZ1000 ) produjeron cámaras bridge con sensores de 1".
Los sensores de los teléfonos con cámara suelen ser mucho más pequeños que los de las cámaras compactas típicas, lo que permite una mayor miniaturización de los componentes eléctricos y ópticos. Los tamaños de sensor de alrededor de 1/6" son comunes en teléfonos con cámara, cámaras web y videocámaras digitales . El sensor de 1/1,83" del Nokia N8 (2010) fue el más grande en un teléfono a fines de 2011. El Nokia 808 (2012) supera a las cámaras compactas con su sensor de 1/1,2" y 41 millones de píxeles. [19]
Sensores digitales de formato medio
Los sensores digitales más grandes de las cámaras disponibles comercialmente se describen como de " formato medio ", en referencia a formatos de película de dimensiones similares. Aunque la película de formato medio más común, el rollo 120 , tiene 6 cm (2,4 pulgadas) de ancho y se suele tomar en formato cuadrado, los tamaños de sensor digital de "formato medio" más comunes son de aproximadamente 48 mm × 36 mm (1,9 pulgadas × 1,4 pulgadas), que es aproximadamente el doble del tamaño de un formato de sensor DSLR de fotograma completo .
Los sensores CCD disponibles incluyen el respaldo digital P65+ de Phase One con un sensor de 53,9 mm × 40,4 mm (2,12 pulgadas × 1,59 pulgadas) de Dalsa que contiene 60,5 megapíxeles [20] y la DSLR "S-System" de Leica con un sensor de 45 mm × 30 mm (1,8 pulgadas × 1,2 pulgadas) que contiene 37 megapíxeles. [21] En 2010, Pentax lanzó la DSLR de formato medio 645D de 40 MP con un sensor CCD de 44 mm × 33 mm (1,7 pulgadas × 1,3 pulgadas); [22] los modelos posteriores de la serie 645 mantuvieron el mismo tamaño de sensor pero reemplazaron el CCD con un sensor CMOS. En 2016, Hasselblad anunció la X1D, una cámara sin espejo de formato medio de 50 MP , con un sensor CMOS de 44 mm × 33 mm (1,7 pulgadas × 1,3 pulgadas). [23] A finales de 2016, Fujifilm también anunció su nueva Fujifilm GFX 50S de formato medio, sin espejo , que entra al mercado, con un sensor CMOS de 43,8 mm × 32,9 mm (1,72 pulgadas × 1,30 pulgadas) y 51,4 MP. [24] [25]
Tabla de formatos y tamaños de sensores

Los tamaños de los sensores se expresan en pulgadas porque en el momento de la popularización de los sensores de imágenes digitales se utilizaban para reemplazar los tubos de las cámaras de vídeo . Los tubos de las cámaras de vídeo circulares de 1" de diámetro exterior comunes tienen un área fotosensible rectangular de aproximadamente16 mm en diagonal, por lo que un sensor digital con unaEl tamaño diagonal de 16 mm es equivalente a un tubo de video de 1". El nombre de un sensor digital de 1" debería leerse con mayor precisión como sensor "equivalente a un tubo de cámara de video de una pulgada". Los descriptores de tamaño de sensor de imagen digital actuales son el tamaño equivalente al tubo de cámara de video, no el tamaño real del sensor. Por ejemplo, un sensor de 1" tiene una medida diagonal de16 milímetros . [26] [27]
Los tamaños se expresan a menudo como una fracción de pulgada, con un uno en el numerador y un número decimal en el denominador. Por ejemplo, 1/2,5 se convierte en 2/5 como una fracción simple , o 0,4 como un número decimal. Este sistema de "pulgadas" da un resultado de aproximadamente 1,5 veces la longitud de la diagonal del sensor. Esta medida de " formato óptico " se remonta a la forma en que se expresaban los tamaños de imagen de las cámaras de vídeo utilizadas hasta finales de la década de 1980, haciendo referencia al diámetro exterior de la envoltura de vidrio del tubo de la cámara de vídeo . David Pogue, de The New York Times, afirma que "el tamaño real del sensor es mucho más pequeño que lo que publican las empresas de cámaras: aproximadamente un tercio más pequeño". Por ejemplo, una cámara que anuncia un sensor de 1/2,7" no tiene un sensor con una diagonal de 0,37 pulgadas (9,4 mm); en cambio, la diagonal está más cerca de 0,26 pulgadas (6,6 mm). [28] [29] [30] En lugar de "formatos", estos tamaños de sensor a menudo se denominan tipos , como en "CCD de tipo 1/2 pulgada".
Debido a que los formatos de sensor basados en pulgadas no están estandarizados, sus dimensiones exactas pueden variar, pero las que se enumeran son típicas. [29] Las áreas de sensor enumeradas abarcan más de un factor de 1000 y son proporcionales a la máxima recolección posible de luz y resolución de imagen (misma velocidad de lente , es decir, número f mínimo ), pero en la práctica no son directamente proporcionales al ruido de la imagen o la resolución debido a otras limitaciones. Ver comparaciones. [31] [32] También se incluyen tamaños de formato de película, para comparación. Los ejemplos de aplicación de teléfono o cámara pueden no mostrar los tamaños exactos de sensor.
| Tipo | Diagonal (mm) | Ancho (mm) | Altura (mm) | Relación de aspecto | Área ( mm2 ) | Paradas (área) [A] | Factor de cultivo [B] |
|---|---|---|---|---|---|---|---|
| 1/10" | 1.60 | 1.28 | 0,96 | 4:3 | 1.23 | -9,46 | 27.04 |
| 1/8" (Sony DCR-SR68, DCR-DVD110E) | 2.00 | 1.60 | 1.20 | 4:3 | 1,92 | -8,81 | 21,65 |
| 1/6" (Panasonic SDR-H20, SDR-H200) | 3.00 | 2.40 | 1,80 | 4:3 | 4.32 | -7,64 | 14.14 |
| 1/4" [33] | 4,50 | 3.60 | 2,70 | 4:3 | 9.72 | -6,47 | 10.81 |
| 1/3,6" ( Nokia Lumia 720 ) [34] | 5.00 | 4.00 | 3.00 | 4:3 | 12.0 | -6,17 | 8.65 |
| 1/3,2" ( iPhone 5 ) [35] | 5.68 | 4.54 | 3.42 | 4:3 | 15,50 | -5,80 | 7.61 |
| Lente Sony EXMOR IMX351 de 1/3,09" [36] | 5.82 | 4.66 | 3.5 | 4:3 | 16.3 | -5,73 | 7.43 |
| Fotograma de película estándar de 8 mm | 5,94 | 4.8 | 3.5 | 11:8 | 16.8 | -5,68 | 7.28 |
| 1/3" ( iPhone 5S , iPhone 6 , LG G3 [37] ) | 6.00 | 4.80 | 3.60 | 4:3 | 17.30 | -5,64 | 7.21 |
| Lente Sony EXMOR IMX322 de 1/2,9" [38] | 6.23 | 4,98 | 3.74 | 4:3 | 18.63 | -5,54 | 6.92 |
| Zoom Fujifilm 2800 de 1/2,7" | 6.72 | 5.37 | 4.04 | 4:3 | 21,70 | -5,32 | 6.44 |
| Fotograma de película Super 8 mm | 7.04 | 5,79 | 4.01 | 13:9 | 23.22 | -5,22 | 6.15 |
| 1/2,5" ( Nokia Lumia 1520 , Sony Cyber-shot DSC-T5 , iPhone XS [39] ) | 7.18 | 5,76 | 4.29 | 4:3 | 24,70 | -5,13 | 6.02 |
| 1/2,3" ( Pentax Q , Sony Cyber-shot DSC-W330, GoPro HERO3, Panasonic HX-A500, Google Pixel/Pixel+, DJI Phantom 3 [40] /Mavic 2 Zoom [41] ), Nikon P1000 / P900 | 7.66 | 6.17 | 4.55 | 4:3 | 28,50 | −4,94 | 5.64 |
| Cámara Sony Exmor IMX220 de 1/2,3" [42] | 7.87 | 6.30 | 4.72 | 4:3 | 29,73 | -4,86 | 5.49 |
| 1/2" ( Fujifilm HS30EXR , Xiaomi Mi 9 , OnePlus 7 , Espros EPC 660, DJI Mavic Air 2) | 8.00 | 6.40 | 4.80 | 4:3 | 30,70 | -4,81 | 5.41 |
| 1/1,8" ( Nokia N8 ) (Olympus C-5050, C-5060, C-7070) | 8,93 | 7.18 | 5.32 | 4:3 | 38.20 | -4,50 | 4.84 |
| 1/1,7" ( Pentax Q7 , Canon G10, G15, Huawei P20 Pro , Huawei P30 Pro , Huawei Mate 20 Pro ) | 9,50 | 7.60 | 5.70 | 4:3 | 43.30 | -4,32 | 4.55 |
| 1/1,6" (Fujifilm f200exr [1]) | 10.07 | 8.08 | 6.01 | 4:3 | 48,56 | -4,15 | 4.30 |
| 2/3" ( Nokia Lumia 1020 , Fujifilm X10, X20, XF1) | 11.00 | 8.80 | 6.60 | 4:3 | 58.10 | -3,89 | 3.93 |
| 1/1,33" ( Samsung Galaxy S20 Ultra ) [43] | 12 | 9.6 | 7.2 | 4:3 | 69.12 | -3,64 | 3.58 |
| Fotograma de película estándar de 16 mm | 12,70 | 10.26 | 7,49 | 11:8 | 76,85 | -3,49 | 3.41 |
| 1/1,2" ( Nokia 808 PureView ) | 13.33 | 10.67 | 8.00 | 4:3 | 85.33 | -3,34 | 3.24 |
| 1/1.12" ( Xiaomi Mi 11 Ultra ) | 14.29 | 11.43 | 8.57 | 4:3 | 97,96 | 3.03 | |
| Cámara Blackmagic Pocket Cinema y cámara Blackmagic Studio | 14.32 | 12.48 | 7.02 | 16:9 | 87.6 | -3,30 | 3.02 |
| Fotograma de película Super 16 mm | 14.54 | 12.52 | 7.41 | 5:3 | 92,80 | -3,22 | 2,97 |
| 1" ( Nikon CX , Sony RX100 , Sony RX10 , Sony ZV1, Samsung NX Mini ) | 15,86 | 13.20 | 8.80 | 3:2 | 116 | -2,89 | 2.72 |
| Bolex digital d16 de 1" | 16.00 | 12,80 | 9.60 | 4:3 | 123 | -2,81 | 2,70 |
| Cámara Kodak DCS -200 de 1" | 16.81 | 14.00 | 9.30 | 3:2 | 130.2 | -2,73 | 2.57 |
| Pantalla Sony IMX253 de 1,1" [44] | 17.46 | 14.10 | 10.30 | 11:8 | 145 | -2,57 | 2.47 |
| Cámara de cine Blackmagic EF | 18.13 | 15.81 | 8.88 | 16:9 | 140 | -2,62 | 2.38 |
| Cámara de cine de bolsillo Blackmagic 4K | 21.44 | 18,96 | 10 | 19:10 | 190 | -2,19 | 2.01 |
| Cuatro Tercios , Micro Cuatro Tercios ("4/3", "m4/3") | 21.60 | 17.30 | 13 | 4:3 | 225 | -1,94 | 2.00 |
| Cámara de producción Blackmagic/URSA/URSA Mini 4K | 24.23 | 21.12 | 11.88 | 16:9 | 251 | -1,78 | 1,79 |
| Cámara Canon PowerShot G1 X Mark II de 1,5" | 23.36 | 18,70 | 14 | 4:3 | 262 | -1,72 | 1,85 |
| Techniscope de 2 perforaciones y "35 mm" | 23,85 | 21,95 | 9.35 | 7:3 | 205.23 | -2,07 | 1.81 |
| Foveon X3 original de Sigma | 24,90 | 20,70 | 13,80 | 3:2 | 286 | -1,60 | 1,74 |
| DRAGÓN ROJO 4.5K (CUERVO) | 25,50 | 23.00 | 10.80 | 19:9 | 248,4 | -1,80 | 1.66 |
| "Super 35 mm" 2 perforaciones | 26,58 | 24,89 | 9.35 | 8:3 | 232,7 | -1,89 | 1.62 |
| Canon EF-S , APS-C | 26,82 | 22.30 | 14,90 | 3:2 | 332 | -1,38 | 1.61 |
| Fotograma de película estándar de 35 mm (película) | 27.20 | 22.0 | 16.0 | 11:8 | 352 | -1,30 | 1,59 |
| Cámara Blackmagic URSA Mini/Pro 4.6K | 29 | 25.34 | 14.25 | 16:9 | 361 | -1,26 | 1.49 |
| APS-C ( Sony α , Sony E , Nikon DX , Pentax K , Samsung NX , Fuji X ) | 28.2–28.4 | 23.6–23.7 | 15,60 | 3:2 | 368–370 | -1,23 a-1,22 | 1,52–1,54 |
| Película Super 35 mm 3 perforaciones | 28.48 | 24,89 | 13.86 | 9:5 | 344,97 | -1,32 | 1.51 |
| DRAGÓN ROJO 5K S35 | 28.9 | 25.6 | 13.5 | 17:9 | 345.6 | -1,32 | 1.49 |
| Película Super 35 mm de 4 perforaciones | 31.11 | 24,89 | 18.66 | 4:3 | 464 | -0,90 | 1.39 |
| Canon APS-H | 33,50 | 27,90 | 18,60 | 3:2 | 519 | -0,74 | 1.29 |
| ARRI ALEV III ( ALEXA SXT , ALEXA MINI , AMIRA), RED HELIUM 8K S35 | 33,80 | 29,90 | 15,77 | 17:9 | 471,52 | -0,87 | 1.28 |
| DRAGÓN ROJO 6K S35 | 34,50 | 30.7 | 15.8 | 35:18 | 485.06 | -0,83 | 1.25 |
| Película de 35 mm de fotograma completo ( Canon EF , Nikon FX , Pentax K-1 , Sony α , Sony FE , Leica M ) | 43.1–43.3 | 35.8–36 | 23.9–24 | 3:2 | 856–864 | 0 | 1.0 |
| ARRI ALEXA LF | 44,71 | 36,70 | 25,54 | 13:9 | 937.32 | 0,12 | 0,96 |
| MONSTRO ROJO 8K VV, Panavision Millenium DXL2 | 46.31 | 40,96 | 21.60 | 17:9 | 884,74 | 0,03 | 0,93 |
| Leica S | 54 | 45 | 30 | 3:2 | 1350 | 0,64 | 0,80 |
| Pentax 645D , Hasselblad X1D-50c, Hasselblad H6D-50c, CFV-50c, Fuji GFX 50S [45] [46] | 55 | 43.8 | 32.9 | 4:3 | 1452 | 0,75 | 0,79 |
| Fotograma de película estándar de 65/70 mm | 57.30 | 52,48 | 23.01 | 7:3 | 1208 | 0,48 | 0,76 |
| ARRI ALEXA 65 | 59,86 | 54.12 | 25,58 | 19:9 | 1384.39 | 0,68 | 0,72 |
| Cámara CCD Kodak KAF 39000 [47] | 61.30 | 49 | 36,80 | 4:3 | 1803 | 1.06 | 0,71 |
| Hoja AFi 10 | 66,57 | 56 | 36 | 14:9 | 2016 | 1.22 | 0,65 |
| Formato medio ( Hasselblad H5D-60c, Hasselblad H6D-100c) [48] | 67.08 | 53.7 | 40.2 | 4:3 | 2159 | 1.32 | 0,65 |
| Fase Uno P 65+ , IQ160, IQ180 | 67,40 | 53,90 | 40,40 | 4:3 | 2178 | 1.33 | 0,64 |
| Formato medio 6×4,5 cm (también llamado formato 645 ) | 70 | 42 | 56 | 3:4 | 2352 | 1.44 | 0,614 |
| Formato medio 6×6 cm | 79 | 56 | 56 | 1:1 | 3136 | 1.86 | 0,538 |
| Fotograma de película IMAX | 87,91 | 70.41 | 52,63 | 4:3 | 3706 | 2.10 | 0,49 |
| Formato medio 6×7 cm | 89.6 | 70 | 56 | 5:4 | 3920 | 2.18 | 0,469 |
| Formato medio 6×8 cm | 94.4 | 76 | 56 | 3:4 | 4256 | 2.30 | 0,458 |
| Formato medio 6×9 cm | 101 | 84 | 56 | 3:2 | 4704 | 2.44 | 0,43 |
| Película de gran formato 4×5 pulgadas | 150 | 121 | 97 | 5:4 | 11737 | 3,76 | 0,29 |
| Película de gran formato 5×7 pulgadas | 210 | 178 | 127 | 7:5 | 22606 | 4.71 | 0,238 |
| Película de gran formato 8×10 pulgadas | 300 | 254 | 203 | 5:4 | 51562 | 5,90 | 0,143 |
- ^ Se define aquí como el número equivalente de paradas perdidas (o ganadas, si es positivo) debido al área del sensor en relación con un área completa.Marco de 35 mm (36 mm × 24 mm ). Calculado como
- ^ Se define aquí como la relación entre la diagonal de un cuadrado completo.Marco de 35 mm al del formato del sensor, es decir
Véase también
- Cámara réflex digital de fotograma completo
- Tamaño del sensor y ángulo de visión
- Longitud focal equivalente a 35 mm
- Formato de película
- Fotografía digital versus fotografía en película
- Lista de cámaras de vídeo con lentes intercambiables y sensores grandes
- Lista de sensores utilizados en cámaras digitales
- Ángulo de visión
- Factor de cultivo
- Campo de visión
Notas
- ^ Este efecto se ha observado en la práctica, como se registra en el artículo de DxOmark 'F-stop blues' [15]
- ^ Aptina analiza con cierto detalle la relativa eficacia de estas estratagemas. [16]
Notas a pie de página y referencias
- ^ "¿Qué es la equivalencia y por qué debería importarme?". DP Review . 2014-07-07 . Consultado el 2017-05-03 .
- ^ ab Fellers, Thomas J.; Davidson, Michael W. "Fuentes de ruido CCD y relación señal-ruido". Hamamatsu Corporation . Consultado el 20 de noviembre de 2013 .
- ^ Aptina Imaging Corporation. "Aprovechamiento de la tecnología de píxeles de respuesta dinámica para optimizar el rango dinámico entre escenas" (PDF) . Aptina Imaging Corporation . Consultado el 17 de diciembre de 2011 .
- ^ Loukianova, Natalia V.; Folkerts, Hein Otto; Maas, Joris PV; Verbugt, Joris PV; Daniël WE Mierop, Adri J.; Hoekstra, Willem; Roks, Edwin y Theuwissen, Albert JP (enero de 2003). "Modelado de corriente de fuga de estructuras de prueba para la caracterización de corriente oscura en sensores de imagen CMOS" (PDF) . IEEE Transactions on Electron Devices . 50 (1): 77–83. Bibcode :2003ITED...50...77L. doi :10.1109/TED.2002.807249 . Consultado el 17 de diciembre de 2011 .
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ "Dark Count". Apogee Imaging Systems . Consultado el 17 de diciembre de 2011 .
- ^ Kavusi, Sam; El Gamal, Abbas (2004). "Estudio cuantitativo de arquitecturas de sensores de imagen de alto rango dinámico" (PDF) . En Blouke, Morley M; Sampat, Nitin; Motta, Ricardo J (eds.). Sensores y sistemas de cámara para aplicaciones científicas, industriales y de fotografía digital V . Vol. 5301. págs. 264–275. Bibcode :2004SPIE.5301..264K. doi :10.1117/12.544517. S2CID 14550103 . Consultado el 17 de diciembre de 2011 .
- ^ Osuna, Rubén; García, Efraín. "¿Los sensores" superan "las lentes?". El paisaje luminoso. Archivado desde el original el 2 de enero de 2010 . Consultado el 21 de diciembre de 2011 .
- ^ Boreman, Glenn D. (2001). Función de transferencia de modulación en sistemas ópticos y electroópticos. SPIE Press. pág. 120. ISBN 978-0-8194-4143-0.
- ^ Ozaktas, Haldun M; Urey, Hakan; Lohmann, Adolf W. (1994). "Escalamiento de lentes difractivas y refractivas para computación óptica e interconexiones". Óptica Aplicada . 33 (17): 3782–3789. Bibcode :1994ApOpt..33.3782O. doi :10.1364/AO.33.003782. hdl : 11693/13640 . PMID 20885771. S2CID 1384331.
- ^ Goodman, Joseph W (2005). Introducción a la óptica de Fourier, 3.ª edición . Greenwood Village, Colorado: Roberts and Company. pág. 26. ISBN. 978-0-9747077-2-3.
- ^ Nasse, HH "De la serie de artículos sobre nombres de lentes: Tessar" (PDF) . Carl Zeiss AG. Archivado desde el original (PDF) el 13 de mayo de 2012. Consultado el 19 de diciembre de 2011 .
- ^ Simon Crisp (21 de marzo de 2013). "Tamaño del sensor de la cámara: ¿por qué es importante y exactamente qué tan grandes son?" . Consultado el 29 de enero de 2014 .
- ^ Stanislav Utochkin. «Especificación del tamaño del área activa del sensor de imagen» . Consultado el 21 de mayo de 2015 .
- ^ Catrysse, Peter B.; Wandell, Brian A. (2005). "Hoja de ruta para sensores de imagen CMOS: Moore se encuentra con Planck y Sommerfeld" (PDF) . En Sampat, Nitin; Dicarlo, Jeffrey M.; Motta, Ricardo J. (eds.). Fotografía digital . Vol. 5678. pág. 1. Código Bibliográfico :2005SPIE.5678....1C. CiteSeerX 10.1.1.80.1320 . doi :10.1117/12.592483. S2CID 7068027. Archivado desde el original (PDF) el 13 de enero de 2015 . Consultado el 29 de enero de 2012 .
- ^ DxOmark. «F-stop blues». DxOMark Insights . Archivado desde el original el 25 de enero de 2012. Consultado el 29 de enero de 2012 .
- ^ Aptina Imaging Corporation. "Una mirada objetiva a FSI y BSI" (PDF) . Libro blanco de Aptina Technology . Consultado el 29 de enero de 2012 .
- ^ "Nikon presenta la cámara sin espejo con sensor pequeño J1 como parte del sistema Nikon 1", Digital Photography Review.
- ^ "Sensores CMOS de fotograma completo de Canon" (PDF) (Nota de prensa). 2006. Archivado desde el original (PDF) el 28 de octubre de 2012. Consultado el 2 de mayo de 2013 .
- ^ http://europe.nokia.com/PRODUCT_METADATA_0/Products/Phones/8000-series/808/Nokia808PureView_Whitepaper.pdf Documento técnico sobre la tecnología de imágenes PureView de Nokia
- ^ "La gama de productos Phase One P+". PHASE ONE. Archivado desde el original el 2010-08-12 . Consultado el 2010-06-07 .
- ^ "Leica S2 con un sensor un 56% más grande que el de formato completo" (Nota de prensa). Leica. 23 de septiembre de 2008. Consultado el 7 de junio de 2010 .
- ^ "Pentax presenta la DSLR de formato medio 645D de 40 MP" (Nota de prensa). Pentax. 10 de marzo de 2010. Consultado el 21 de diciembre de 2010 .
- ^ Johnson, Allison (22 de junio de 2016). «Cámaras sin espejo de formato medio: Hasselblad presenta la X1D». Digital Photography Review . Consultado el 26 de junio de 2016 .
- ^ "Fujifilm anuncia el desarrollo de un nuevo sistema de cámara sin espejo de formato medio "GFX"" (Nota de prensa). Fujifilm . 19 de septiembre de 2016.[ enlace muerto permanente ]
- ^ "La cámara de formato medio GFX 50S de Fujifilm se comercializará en febrero a un precio de 6.500 dólares". 19 de enero de 2017.
- ^ Staff (7 de octubre de 2002). "Making (some) sense out of sensor sizes" ( Digital Photography Review ). Consultado el 29 de junio de 2012 .
- ^ Personal. "Formato del sensor de imagen". Términos y definiciones del glosario de imágenes . SPOT IMAGING SOLUTIONS. Archivado desde el original el 26 de marzo de 2015. Consultado el 3 de junio de 2015 .
- ^ Pogue, David (22 de diciembre de 2010). "Cámaras pequeñas con sensores grandes y cómo compararlas". The New York Times .
- ^ ab Bockaert, Vincent. "Tamaños de sensor: Sistema de cámara: Glosario: Aprender". Digital Photography Review . Archivado desde el original el 25 de enero de 2013. Consultado el 9 de abril de 2012 .
- ^ "Dándole (algo de) sentido a los tamaños de los sensores".
- ^ Calificaciones de los sensores de la cámara Archivado el 21 de marzo de 2012 en Wayback Machine DxOMark
- ^ Recurso de imágenes: Imágenes de muestra Comparómetro Recurso de imágenes
- ^ "Descifrando los tamaños de los sensores: análisis fotográfico" www.photoreview.com.au . Consultado el 22 de septiembre de 2016 .
- ^ Nokia Lumia 720 – Especificaciones completas del teléfono, GSMArena.com, 25 de febrero de 2013 , consultado el 21 de septiembre de 2013
- ^ Tamaño del sensor de la cámara: ¿por qué es importante y exactamente qué tan grandes son?, Gizmag, 21 de marzo de 2013 , consultado el 19 de junio de 2013
- ^ "Sensor de imagen CMOS de 16 megapíxeles y 5,822 mm en diagonal (tipo 1/3,09) con píxeles cuadrados para cámaras en color" (PDF) . Sony. Archivado desde el original (PDF) el 16 de octubre de 2019 . Consultado el 16 de octubre de 2019 .
- ^ Comparación de las especificaciones del iPhone, PhoneArena
- ^ "Sensor de imagen CMOS de 6,23 mm en diagonal (tipo 1/2,9) con píxeles cuadrados para cámaras en color" (PDF) . Sony. 2015 . Consultado el 3 de abril de 2019 .
- ^ "El desmontaje del iPhone XS Max revela un nuevo sensor con más píxeles de enfoque". Digital Photography Review. 27 de septiembre de 2018. Consultado el 1 de marzo de 2019 .
- ^ "Phantom 3 Professional: deja volar tu creatividad con una cámara 4K en el cielo. - DJI". DJI Oficial . Consultado el 1 de diciembre de 2019 .
- ^ "DJI - El líder mundial en drones/cuadricópteros con cámara para fotografía aérea". DJI Official . Consultado el 1 de diciembre de 2019 .
- ^ "Sensor de imagen CMOS de 20,7 megapíxeles y 7,87 mm diagonal (tipo 1/2,3) con píxeles cuadrados para cámaras en color" (PDF) . Sony. Septiembre de 2014. Archivado desde el original (PDF) el 3 de abril de 2019 . Consultado el 3 de abril de 2019 .
- ^ "Samsung presenta oficialmente el sensor de cámara móvil ISOCELL Bright HMX de 108 MP". Digital Photography Review. 12 de agosto de 2019. Consultado el 16 de febrero de 2021 .
- ^ "Sensor de imagen CMOS monocromo y en color de 17,6 mm (tipo 1.1) con diagonal de aproximadamente 12,37 millones de píxeles efectivos" (PDF) . Sony. Marzo de 2016. Archivado desde el original (PDF) el 15 de diciembre de 2017 . Consultado el 3 de abril de 2019 .
- ^ "Ficha técnica de la Hasselblad X1D-II 50c" (PDF) . Hasselblad. 2019-06-01 . Consultado el 2022-04-09 .
- ^ "Especificaciones de la GFX 50s". Fujifilm. 17 de enero de 2019. Consultado el 9 de abril de 2022 .
- ^ SENSOR DE IMAGEN KODAK KAF-39000, ESPECIFICACIÓN DEL RENDIMIENTO DEL DISPOSITIVO (PDF) , KODAK, 30 de abril de 2010 , consultado el 9 de febrero de 2014
- ^ Cámara DSLR de formato medio Hasselblad H5D-60, B&H PHOTO VIDEO , consultado el 19 de junio de 2013
Enlaces externos
- Eric Fossum: Photons to Bits and Beyond: The Science & Technology of Digital, 13 de octubre de 2011 (vídeo de la conferencia en YouTube)
- Joseph James: Equivalencia en Joseph James Photography
- Simon Tindemans: Parámetros fotográficos alternativos: un enfoque independiente del formato en 21stcenturyshoebox
- Modos ISO altos para cámaras compactas: cómo separar los hechos de las exageraciones en dpreview.com, mayo de 2007
- El mejor compromiso para una cámara compacta es un sensor con 6 millones de píxeles o mejor aún, un sensor con un tamaño de píxel de >3μm en 6mpixel.org
- [2] en hasselblad.com






















![{\displaystyle \mathrm {MTF} \left({\frac {\xi }{\xi _{\mathrm {corte} }}}\right)={\frac {2}{\pi }}\left\{\cos ^{-1}\left({\frac {\xi }{\xi _{\mathrm {corte} }}}\right)-\left({\frac {\xi }{\xi _{\mathrm {corte} }}}\right)\left[1-\left({\frac {\xi }{\xi _{\mathrm {corte} }}}\right)^{2}\right]^{\frac {1}{2}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2df679bc046c28caa3d3f26b8db34e88d924319e)















