Puntuación estándar
¿A cuántas desviaciones estándar de la media se encuentra un dato observado?

Comparación de los distintos métodos de calificación en una distribución normal , incluidos: desviaciones estándar , porcentajes acumulados, percentiles equivalentes, puntuaciones z y puntuaciones T.

En estadística , la puntuación estándar es el número de desviaciones estándar por las cuales el valor de una puntuación bruta (es decir, un valor observado o un punto de datos) está por encima o por debajo del valor medio de lo que se está observando o midiendo. Las puntuaciones brutas por encima de la media tienen puntuaciones estándar positivas, mientras que las que están por debajo de la media tienen puntuaciones estándar negativas.

Se calcula restando la media de la población de una puntuación bruta individual y luego dividiendo la diferencia por la desviación estándar de la población . Este proceso de convertir una puntuación bruta en una puntuación estándar se denomina estandarización o normalización (sin embargo, "normalizar" puede referirse a muchos tipos de proporciones; consulte Normalización para obtener más información).

Las puntuaciones estándar se denominan comúnmente puntuaciones z ; ambos términos pueden utilizarse indistintamente, como en este artículo. Otros términos equivalentes en uso incluyen valor z , estadística z , puntuación normal , variable estandarizada y pull en física de alta energía . [1] [2]

Para calcular una puntuación z es necesario conocer la media y la desviación estándar de la población completa a la que pertenece un punto de datos; si solo se tiene una muestra de observaciones de la población, entonces el cálculo análogo utilizando la media de la muestra y la desviación estándar de la muestra produce la estadística t .

Cálculo

Si se conocen la media y la desviación estándar de la población, una puntuación bruta x se convierte en una puntuación estándar mediante [3]

el = incógnita − micras σ {\displaystyle z={x-\mu \sobre \sigma }}

dónde:

μ es la media de la población,
σ es la desviación estándar de la población.

El valor absoluto de z representa la distancia entre esa puntuación bruta x y la media de la población en unidades de desviación estándar. z es negativo cuando la puntuación bruta está por debajo de la media, positivo cuando está por encima.

Para calcular z con esta fórmula es necesario utilizar la media y la desviación estándar de la población, no la media o la desviación estándar de la muestra. Sin embargo, conocer la media y la desviación estándar verdaderas de una población suele ser una expectativa poco realista, excepto en casos como las pruebas estandarizadas , donde se mide a toda la población.

Cuando se desconocen la media y la desviación estándar de la población, la puntuación estándar se puede estimar utilizando la media y la desviación estándar de la muestra como estimaciones de los valores de la población. [4] [5] [6] [7]

En estos casos, la puntuación z viene dada por

el = incógnita − incógnita ¯ S {\displaystyle z={x-{\bar {x}} \sobre S}}

dónde:

incógnita ¯ {\estilo de visualización {\barra {x}}} es la media de la muestra,
S es la desviación estándar de la muestra.

Aunque siempre debe indicarse, a menudo no se hace la distinción entre el uso de estadísticas de población y de muestra. En ambos casos, el numerador y el denominador de las ecuaciones tienen las mismas unidades de medida, de modo que las unidades se cancelan mediante la división y z queda como una cantidad adimensional .

Aplicaciones

Prueba Z

La puntuación z se utiliza a menudo en la prueba z de las pruebas estandarizadas, que es el análogo de la prueba t de Student para una población cuyos parámetros se conocen, en lugar de estimarse. Como es muy poco habitual conocer la población completa, la prueba t se utiliza mucho más ampliamente.

Intervalos de predicción

La puntuación estándar se puede utilizar en el cálculo de intervalos de predicción . Un intervalo de predicción [ L , U ], que consta de un punto final inferior designado L y un punto final superior designado U , es un intervalo tal que una observación futura X se encontrará en el intervalo con alta probabilidad , es decir gamma {\estilo de visualización \gamma}

PAG ( yo < incógnita < tú ) = gamma , {\displaystyle P(L<X<U)=\gamma,}

Para la puntuación estándar Z de X se obtiene: [8]

PAG ( yo − micras σ < O < tú − micras σ ) = gamma . {\displaystyle P\left({\frac {L-\mu }{\sigma }}<Z<{\frac {U-\mu }{\sigma }}\right)=\gamma .}

Determinando el cuartil z tal que

PAG ( − el < O < el ) = gamma {\displaystyle P\left(-z<Z<z\right)=\gamma}

Sigue lo siguiente:

yo = micras − el σ ,   tú = micras + el σ {\displaystyle L=\mu -z\sigma ,\ U=\mu +z\sigma }

Control de procesos

En aplicaciones de control de procesos, el valor Z proporciona una evaluación del grado en el cual un proceso está funcionando fuera del objetivo.

Comparación de puntuaciones medidas en diferentes escalas: ACT y SAT

La puntuación z del estudiante A fue 1, lo que significa que el estudiante A se ubicó 1 desviación estándar por encima de la media. Por lo tanto, el estudiante A obtuvo un percentil 84,13 en el examen SAT.

Cuando las puntuaciones se miden en diferentes escalas, se pueden convertir en puntuaciones z para facilitar la comparación. Dietz et al. [9] dan el siguiente ejemplo, comparando las puntuaciones de los estudiantes en los exámenes SAT y ACT (antiguos) de secundaria. La tabla muestra la media y la desviación estándar de las puntuaciones totales en el SAT y el ACT. Supongamos que el estudiante A obtuvo 1800 puntos en el SAT y el estudiante B 24 puntos en el ACT. ¿Qué estudiante obtuvo un mejor resultado en relación con los demás examinados?

SE SENTÓACTO
Significar150021
Desviación estándar3005
La puntuación z del estudiante B fue 0,6, lo que significa que el estudiante B se encontraba 0,6 desviaciones estándar por encima de la media. Por lo tanto, el estudiante B obtuvo un rendimiento en el percentil 72,57 en el examen SAT.

La puntuación z del estudiante A es el = incógnita − micras σ = 1800 − 1500 300 = 1 {\displaystyle z={x-\mu \sobre \sigma }={1800-1500 \sobre 300}=1}

La puntuación z del estudiante B es el = incógnita − micras σ = 24 − 21 5 = 0.6 {\displaystyle z={x-\mu \sobre \sigma }={24-21 \sobre 5}=0,6}

Debido a que el estudiante A tiene una puntuación z más alta que el estudiante B, el estudiante A tuvo un mejor desempeño en comparación con otros examinados que el estudiante B.

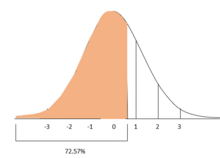
Porcentaje de observaciones por debajo de una puntuación z

Continuando con el ejemplo de los puntajes ACT y SAT, si se puede suponer además que ambos puntajes se distribuyen normalmente (lo cual es aproximadamente correcto), entonces los puntajes z se pueden usar para calcular el porcentaje de examinados que recibieron puntajes más bajos que los estudiantes A y B.

Análisis de conglomerados y escalamiento multidimensional

“Para algunas técnicas multivariadas, como el escalamiento multidimensional y el análisis de conglomerados, el concepto de distancia entre las unidades de los datos suele ser de considerable interés e importancia… Cuando las variables de un conjunto de datos multivariados están en escalas diferentes, tiene más sentido calcular las distancias después de alguna forma de estandarización”. [10]

Análisis de componentes principales

En el análisis de componentes principales, "las variables medidas en diferentes escalas o en una escala común con rangos muy diferentes suelen estar estandarizadas". [11]

Importancia relativa de las variables en la regresión múltiple: coeficientes de regresión estandarizados

La estandarización de variables antes del análisis de regresión múltiple se utiliza a veces como ayuda para la interpretación. [12] (página 95) afirma lo siguiente.

"La pendiente de regresión estandarizada es la pendiente en la ecuación de regresión si X e Y están estandarizados... La estandarización de X e Y se realiza restando las medias respectivas de cada conjunto de observaciones y dividiéndolas por las respectivas desviaciones estándar... En la regresión múltiple, donde se utilizan varias variables X, los coeficientes de regresión estandarizados cuantifican la contribución relativa de cada variable X".

Sin embargo, Kutner et al. [13] (p. 278) hacen la siguiente advertencia: "... hay que ser cauteloso al interpretar los coeficientes de regresión, ya sean estandarizados o no. La razón es que cuando las variables predictoras están correlacionadas entre sí, ... los coeficientes de regresión se ven afectados por las otras variables predictoras del modelo... Las magnitudes de los coeficientes de regresión estandarizados se ven afectadas no sólo por la presencia de correlaciones entre las variables predictoras, sino también por los espaciamientos de las observaciones de cada una de estas variables. A veces, estos espaciamientos pueden ser bastante arbitrarios. Por lo tanto, normalmente no es prudente interpretar las magnitudes de los coeficientes de regresión estandarizados como reflejo de la importancia comparativa de las variables predictoras".

Estandarización en estadística matemática

En estadística matemática , una variable aleatoria X se estandariza restando su valor esperado y dividiendo la diferencia por su desviación estándar. mi ⁡ [ incógnita ] {\displaystyle \nombre del operador {E} [X]} σ ( incógnita ) = Variedad ⁡ ( incógnita ) : {\displaystyle \sigma (X)={\sqrt {\operatorname {Var} (X)}}:}

O = incógnita − mi ⁡ [ incógnita ] σ ( incógnita ) {\displaystyle Z={X-\nombre del operador {E} [X] \sobre \sigma (X)}}

Si la variable aleatoria en consideración es la media muestral de una muestra aleatoria de X :   incógnita 1 , … , incógnita norte {\displaystyle \ X_{1},\puntos ,X_{n}}

incógnita ¯ = 1 norte ∑ i = 1 norte incógnita i {\displaystyle {\bar {X}}={1 \sobre n}\suma _{i=1}^{n}X_{i}}

Entonces la versión estandarizada es

O = incógnita ¯ − mi ⁡ [ incógnita ¯ ] σ ( incógnita ) / norte {\displaystyle Z={\frac {{\bar {X}}-\nombre del operador {E} [{\bar {X}}]}{\sigma (X)/{\sqrt {n}}}}}
Donde la varianza de la media de la muestra estandarizada se calculó de la siguiente manera:
Variedad ⁡ ( ∑ incógnita i ) = ∑ Variedad ⁡ ( incógnita i ) = norte Variedad ⁡ ( incógnita i ) = norte σ 2 Variedad ⁡ ( incógnita ¯ ) = Variedad ⁡ ( ∑ incógnita i norte ) = 1 norte 2 Variedad ⁡ ( ∑ incógnita i ) = norte σ 2 norte 2 = σ 2 norte {\displaystyle {\begin{array}{l}\operatorname {Var} \left(\sum x_{i}\right)=\sum \operatorname {Var} (x_{i})=n\operatorname {Var} (x_{i})=n\sigma ^{2}\\\operatorname {Var} ({\overline {X}})=\operatorname {Var} \left({\frac {\sum x_{i}}{n}}\right)={\frac {1}{n^{2}}}\operatorname {Var} \left(\sum x_{i}\right)={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}\end{array}}}

Puntuación T

En la evaluación educativa, la puntuación T es una puntuación estándar desplazada en Z y escalada para tener una media de 50 y una desviación estándar de 10. [14] [15] [16]

En las mediciones de densidad ósea, el T-score es el puntaje estándar de la medición en comparación con la población de adultos sanos de 30 años, y tiene una media habitual de 0 y una desviación estándar de 1. [17]

Véase también

Referencias

  1. ^ Mulders, Martijn; Zanderighi, Giulia, eds. (2017). 2015 European School of High-Energy Physics: Bansko, Bulgaria 02 - 15 Sep 2015. CERN Yellow Reports: School Proceedings. Ginebra: CERN. ISBN 978-92-9083-472-4.
  2. ^ Gross, Eilam (6 de noviembre de 2017). "Estadísticas prácticas para física de altas energías". CERN Yellow Reports: Actas escolares . 4/2017: 165–186. doi :10.23730/CYRSP-2017-004.165.
  3. ^ E. Kreyszig (1979). Matemáticas avanzadas para ingeniería (cuarta edición). Wiley. pág. 880, ecuación 5. ISBN 0-471-02140-7.
  4. ^ Spiegel, Murray R.; Stephens, Larry J (2008), Schaum's Outlines Statistics (Cuarta edición), McGraw Hill, ISBN 978-0-07-148584-5
  5. ^ Mendenhall, William; Sincich, Terry (2007), Estadística para la ingeniería y las ciencias (Quinta edición), Pearson / Prentice Hall, ISBN 978-0131877061
  6. ^ Glantz, Stanton A.; Slinker, Bryan K.; Neilands, Torsten B. (2016), Introducción a la regresión aplicada y el análisis de varianza (tercera edición), McGraw Hill, ISBN 978-0-852-2-3 978-0071824118
  7. ^ Aho, Ken A. (2014), Estadística básica y aplicada para biólogos (primera edición), Chapman & Hall / CRC Press, ISBN 978-1439873380
  8. ^ E. Kreyszig (1979). Matemáticas avanzadas para ingeniería (cuarta edición). Wiley. pág. 880, ecuación 6. ISBN 0-471-02140-7.
  9. ^ Diez, David; Barr, Christopher; Çetinkaya-Rundel, Mine (2012), OpenIntro Statistics (segunda edición), openintro.org
  10. ^ Everitt, Brian; Hothorn, Torsten J (2011), Introducción al análisis multivariado aplicado con R , Springer, ISBN 978-1441996497
  11. ^ Johnson, Richard; Wichern, Wichern (2007), Análisis estadístico multivariado aplicado , Pearson/Prentice Hall
  12. ^ Afifi, Abdelmonem; May, Susanne K.; Clark, Virginia A. (2012), Análisis multivariante práctico (Quinta edición), Chapman & Hall/CRC, ISBN 978-1439816806
  13. ^ Kutner, Michael; Nachtsheim, Christopher; Neter, John (204), Modelos de regresión lineal aplicados (cuarta edición), McGraw Hill, ISBN 978-0073014661
  14. ^ John Salvia; James Ysseldyke; Sara Witmer (29 de enero de 2009). Evaluación: en educación especial e inclusiva. Cengage Learning. pp. 43–. ISBN 978-0-547-13437-6.
  15. ^ Edward S. Neukrug; R. Charles Fawcett (1 de enero de 2014). Fundamentos de evaluación y pruebas: una guía práctica para consejeros, trabajadores sociales y psicólogos. Cengage Learning. pp. 133–. ISBN 978-1-305-16183-2.
  16. ^ Randy W. Kamphaus (16 de agosto de 2005). Evaluación clínica de la inteligencia infantil y adolescente. Springer. pp. 123–. ISBN 978-0-387-26299-4.
  17. ^ "Medición de la masa ósea: qué significan los números". Centro Nacional de Recursos sobre Osteoporosis y Enfermedades Óseas Relacionadas del NIH . Instituto Nacional de Salud . Consultado el 5 de agosto de 2017 .

Lectura adicional

  • Carroll, Susan Rovezzi; Carroll, David J. (2002). Estadísticas simplificadas para líderes escolares (edición ilustrada). Rowman & Littlefield. ISBN 978-0-8108-4322-6. Consultado el 7 de junio de 2009 .
  • Larsen, Richard J.; Marx, Morris L. (2000). Introducción a la estadística matemática y sus aplicaciones (tercera edición). pág. 282. ISBN 0-13-922303-7.
  • Calculadora de puntuación z
Obtenido de "https://es.wikipedia.org/w/index.php?title=Puntuación_estándar&oldid=1253910312#Puntuación T"