Dinámica de sistemas
La dinámica de sistemas ( DS ) es un enfoque para comprender el comportamiento no lineal de sistemas complejos a lo largo del tiempo utilizando stocks, flujos , bucles de retroalimentación internos , funciones de tabla y retrasos de tiempo. [1]
Descripción general
La dinámica de sistemas es una metodología y una técnica de modelado matemático para enmarcar, comprender y analizar problemas y cuestiones complejos. Desarrollada originalmente en la década de 1950 para ayudar a los gerentes corporativos a mejorar su comprensión de los procesos industriales, actualmente se utiliza en todo el sector público y privado para el análisis y diseño de políticas. [2]
Los programas de dinámica de sistemas con interfaz gráfica de usuario (GUI) se han desarrollado en versiones fáciles de usar en la década de 1990 y se han aplicado a diversos sistemas. Los modelos de dinámica de sistemas resuelven el problema de la simultaneidad (causalidad mutua) actualizando todas las variables en pequeños incrementos de tiempo con retroalimentaciones positivas y negativas y retrasos de tiempo que estructuran las interacciones y el control. El modelo de dinámica de sistemas más conocido es probablemente The Limits to Growth de 1972. Este modelo predijo que el crecimiento exponencial de la población y el capital, con fuentes y sumideros de recursos finitos y retrasos en la percepción, conduciría al colapso económico durante el siglo XXI bajo una amplia variedad de escenarios de crecimiento.
La dinámica de sistemas es un aspecto de la teoría de sistemas que se utiliza como método para comprender el comportamiento dinámico de sistemas complejos. La base del método es el reconocimiento de que la estructura de cualquier sistema, las múltiples relaciones circulares, entrelazadas y a veces con retraso temporal entre sus componentes, es a menudo tan importante para determinar su comportamiento como los propios componentes individuales. Algunos ejemplos son la teoría del caos y la dinámica social . También se afirma que, dado que a menudo hay propiedades del conjunto que no se pueden encontrar entre las propiedades de los elementos, en algunos casos el comportamiento del conjunto no se puede explicar en términos del comportamiento de las partes.
Historia
La dinámica de sistemas fue creada a mediados de la década de 1950 [3] por el profesor Jay Forrester del Instituto Tecnológico de Massachusetts . En 1956, Forrester aceptó una cátedra en la recién formada Escuela de Administración Sloan del MIT . Su objetivo inicial era determinar cómo su formación en ciencia e ingeniería podía aplicarse, de alguna manera útil, a las cuestiones fundamentales que determinan el éxito o el fracaso de las corporaciones. Las ideas de Forrester sobre los fundamentos comunes que sustentan la ingeniería, que llevaron a la creación de la dinámica de sistemas, fueron desencadenadas, en gran medida, por su participación con los gerentes de General Electric (GE) a mediados de la década de 1950. En ese momento, los gerentes de GE estaban perplejos porque el empleo en sus plantas de electrodomésticos en Kentucky exhibía un ciclo significativo de tres años. El ciclo económico se consideró una explicación insuficiente para la inestabilidad del empleo. A partir de simulaciones manuales (o cálculos) de la estructura de retroalimentación de flujo de existencias de las plantas de GE, que incluían la estructura de toma de decisiones corporativa existente para la contratación y los despidos, Forrester pudo demostrar que la inestabilidad en el empleo de GE se debía a la estructura interna de la empresa y no a una fuerza externa como el ciclo económico. Estas simulaciones manuales fueron el comienzo del campo de la dinámica de sistemas. [2]
A finales de los años 50 y principios de los 60, Forrester y un equipo de estudiantes de posgrado trasladaron el campo emergente de la dinámica de sistemas de la etapa de simulación manual a la etapa de modelado informático formal . Richard Bennett creó el primer lenguaje de modelado informático de dinámica de sistemas llamado SIMPLE (Simulation of Industrial Management Problems with Lots of Equations) en la primavera de 1958. En 1959, Phyllis Fox y Alexander Pugh escribieron la primera versión de DYNAMO (DYNAmic MOdels), una versión mejorada de SIMPLE, y el lenguaje de dinámica de sistemas se convirtió en el estándar de la industria durante más de treinta años. Forrester publicó el primer libro, y todavía clásico, en el campo titulado Industrial Dynamics en 1961. [2]
Desde finales de los años 1950 hasta finales de los años 1960, la dinámica de sistemas se aplicó casi exclusivamente a problemas corporativos/gerenciales. Sin embargo, en 1968, un suceso inesperado hizo que el campo se ampliara más allá del modelado corporativo. John F. Collins , ex alcalde de Boston, fue nombrado profesor visitante de Asuntos Urbanos en el MIT. El resultado de la colaboración Collins-Forrester fue un libro titulado Urban Dynamics . El modelo Urban Dynamics presentado en el libro fue la primera aplicación importante no corporativa de la dinámica de sistemas. [2] En 1967, Richard M. Goodwin publicó la primera edición de su artículo "A Growth Cycle", [4] que fue el primer intento de aplicar los principios de la dinámica de sistemas a la economía. Dedicó la mayor parte de su vida a enseñar lo que llamó "Dinámica económica", que podría considerarse un precursor de la economía moderna del no equilibrio . [5]
La segunda aplicación no corporativa importante de la dinámica de sistemas se produjo poco después de la primera. En 1970, Jay Forrester fue invitado por el Club de Roma a una reunión en Berna, Suiza. El Club de Roma es una organización dedicada a resolver lo que sus miembros describen como el "predicamento de la humanidad", es decir, la crisis global que puede aparecer en algún momento en el futuro, debido a las demandas que la población mundial, en crecimiento exponencial, impone a la capacidad de sustentación de la Tierra (sus fuentes de recursos renovables y no renovables y sus sumideros para la eliminación de contaminantes). En la reunión de Berna, se le preguntó a Forrester si la dinámica de sistemas podría utilizarse para abordar el predicamento de la humanidad. Su respuesta, por supuesto, fue que sí. En el avión de regreso de la reunión de Berna, Forrester creó el primer borrador de un modelo de dinámica de sistemas del sistema socioeconómico mundial. Llamó a este modelo WORLD1. A su regreso a los Estados Unidos, Forrester perfeccionó WORLD1 en preparación para una visita al MIT de miembros del Club de Roma. Forrester denominó a la versión refinada del modelo WORLD2 y publicó WORLD2 en un libro titulado World Dynamics . [2]
Temas de dinámica de sistemas
Los elementos principales de los diagramas de dinámica de sistemas son la retroalimentación, la acumulación de flujos en existencias y los retrasos en el tiempo.
Como ejemplo del uso de la dinámica de sistemas, imaginemos una organización que planea introducir un nuevo e innovador producto de consumo duradero. La organización necesita comprender la posible dinámica del mercado para diseñar planes de marketing y producción.
Diagramas de bucles causales
En la metodología de dinámica de sistemas, un problema o un sistema (por ejemplo, un ecosistema, un sistema político o un sistema mecánico) puede representarse como un diagrama de bucle causal . [6] Un diagrama de bucle causal es un mapa simple de un sistema con todos sus componentes constituyentes y sus interacciones. Al capturar las interacciones y, en consecuencia, los bucles de retroalimentación (ver la figura siguiente), un diagrama de bucle causal revela la estructura de un sistema. Al comprender la estructura de un sistema, se hace posible determinar el comportamiento de un sistema durante un período de tiempo determinado. [7]
El diagrama del bucle causal de la introducción de un nuevo producto podría verse así:

En este diagrama hay dos ciclos de retroalimentación. El ciclo de refuerzo positivo (etiquetado con una R) a la derecha indica que cuantas más personas hayan adoptado el nuevo producto, más fuerte será el impacto de boca en boca. Habrá más referencias al producto, más demostraciones y más reseñas. Esta retroalimentación positiva debería generar ventas que sigan creciendo.
El segundo ciclo de retroalimentación de la izquierda es el refuerzo negativo (o "equilibrio", por lo que se lo denomina B). Es evidente que el crecimiento no puede continuar indefinidamente, porque a medida que más y más personas adoptan, quedan cada vez menos posibles adoptantes.
Ambos bucles de retroalimentación actúan simultáneamente, pero en diferentes momentos pueden tener distinta intensidad. Por lo tanto, se podría esperar un aumento de las ventas en los primeros años y una disminución en los años posteriores. Sin embargo, en general, un diagrama de bucle causal no especifica la estructura de un sistema lo suficiente como para permitir la determinación de su comportamiento a partir de la representación visual únicamente. [8]
Diagramas de stock y flujo
Los diagramas de bucle causal ayudan a visualizar la estructura y el comportamiento de un sistema y a analizarlo cualitativamente. Para realizar un análisis cuantitativo más detallado, un diagrama de bucle causal se transforma en un diagrama de stock y flujo . Un modelo de stock y flujo ayuda a estudiar y analizar el sistema de forma cuantitativa; estos modelos suelen construirse y simularse mediante software informático.
Un stock es el término que designa a cualquier entidad que se acumula o se agota con el tiempo. Un flujo es la tasa de cambio de un stock.

En este ejemplo, hay dos grupos: adoptantes potenciales y adoptantes. Hay un flujo: nuevos adoptantes. Por cada nuevo adoptante, el grupo de adoptantes potenciales disminuye en uno y el grupo de adoptantes aumenta en uno.

Ecuaciones
El verdadero poder de la dinámica de sistemas se aprovecha mediante la simulación. Si bien es posible realizar el modelado en una hoja de cálculo , existen diversos paquetes de software que han sido optimizados para ello.
Los pasos involucrados en una simulación son:
- Definir el límite del problema
- Identificar los stocks y flujos más importantes que modifican estos niveles de stock
- Identificar fuentes de información que impactan los flujos
- Identificar los principales bucles de retroalimentación
- Dibuje un diagrama de bucle causal que vincule los stocks, flujos y fuentes de información.
- Escribe las ecuaciones que determinan los flujos.
- Estimar los parámetros y las condiciones iniciales. Estos pueden estimarse utilizando métodos estadísticos, opiniones de expertos, datos de investigación de mercado u otras fuentes de información pertinentes. [9]
- Simular el modelo y analizar resultados.
En este ejemplo, las ecuaciones que modifican los dos stocks a través del flujo son:
Ecuaciones en tiempo discreto
Lista de todas las ecuaciones en tiempo discreto , en su orden de ejecución en cada año, para los años 1 al 15:
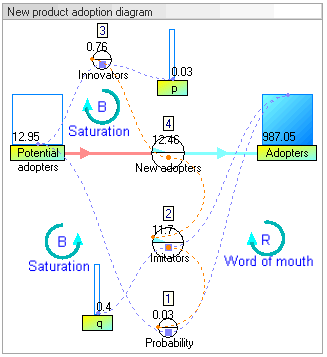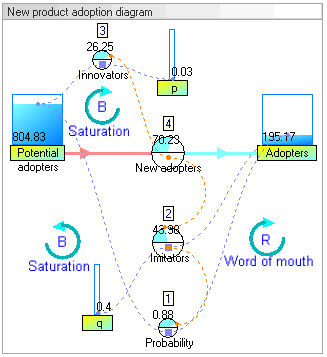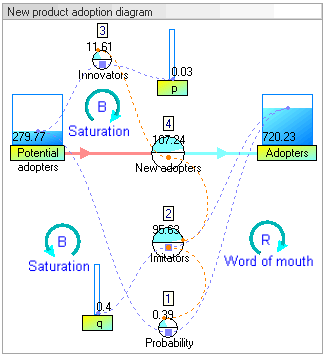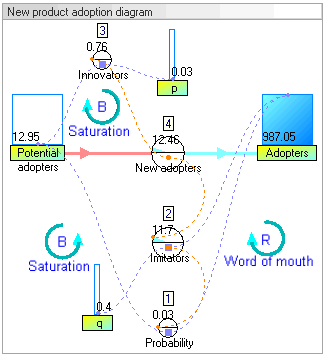
Resultados de simulación dinámica
Los resultados de la simulación dinámica muestran que el comportamiento del sistema sería el de un crecimiento de los adoptantes que seguiría una clásica curva en forma de S.
El aumento de los adoptantes es muy lento al principio, luego crece exponencialmente durante un período y finalmente llega a la saturación.


Ecuaciones en tiempo continuo
Para obtener valores intermedios y una mayor precisión, el modelo puede ejecutarse en tiempo continuo: multiplicamos el número de unidades de tiempo y dividimos proporcionalmente los valores que modifican los niveles de stock. En este ejemplo multiplicamos los 15 años por 4 para obtener 60 trimestres, y dividimos el valor del flujo por 4.
La división del valor es la más sencilla con el método de Euler , pero se podrían emplear otros métodos en su lugar, como el de Runge-Kutta .
Lista de ecuaciones en tiempo continuo para trimestres = 1 a 60 :
- Son las mismas ecuaciones que en la sección Ecuación en tiempo discreto anterior, excepto que las ecuaciones 4.1 y 4.2 se sustituyen por las siguientes:
- En el diagrama de stock y flujo que aparece a continuación, el flujo intermedio 'Nuevos adoptantes de válvulas' calcula la ecuación:

Solicitud
La dinámica de sistemas ha encontrado aplicaciones en una amplia gama de áreas, por ejemplo, población , agricultura, [10] sistemas ecológicos y económicos , que generalmente interactúan fuertemente entre sí.
La dinámica de sistemas tiene varias aplicaciones de gestión "de memoria". Son una herramienta potente para:
- Enseñar reflejos de pensamiento sistémico a las personas que reciben coaching.
- Analizar y comparar suposiciones y modelos mentales sobre cómo funcionan las cosas.
- Obtenga información cualitativa sobre el funcionamiento de un sistema o las consecuencias de una decisión.
- Reconocer arquetipos de sistemas disfuncionales en la práctica cotidiana.
Se utiliza un software informático para simular un modelo de dinámica de sistemas de la situación que se está estudiando. La ejecución de simulaciones hipotéticas para probar determinadas políticas en un modelo de este tipo puede ayudar en gran medida a comprender cómo cambia el sistema con el tiempo. La dinámica de sistemas es muy similar al pensamiento sistémico y construye los mismos diagramas de bucle causal de sistemas con retroalimentación. Sin embargo, la dinámica de sistemas suele ir más allá y utiliza la simulación para estudiar el comportamiento de los sistemas y el impacto de políticas alternativas. [11]
La dinámica de sistemas se ha utilizado para investigar las dependencias de recursos y los problemas resultantes en el desarrollo de productos. [12] [13]
El economista Steve Keen desarrolló un enfoque de dinámica de sistemas para la macroeconomía , conocido como Minsky . [14] Este se ha utilizado para modelar con éxito el comportamiento económico mundial desde la aparente estabilidad de la Gran Moderación hasta la repentina e inesperada crisis financiera de 2007-08 .
Ejemplo: Crecimiento y declive de las empresas
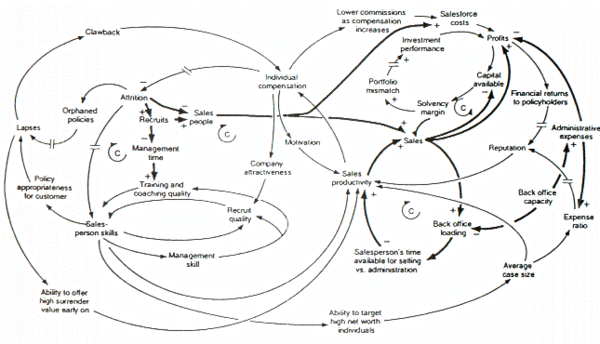
La figura anterior es un diagrama de bucle causal de un modelo de dinámica de sistemas creado para examinar las fuerzas que pueden ser responsables del crecimiento o la caída de las compañías de seguros de vida en el Reino Unido . Vale la pena mencionar varias de las características de esta figura. La primera es que los bucles de retroalimentación negativos del modelo se identifican con C , que significan bucles de contrarrestación . La segunda es que se utilizan barras dobles para indicar lugares donde hay un retraso significativo entre las causas (es decir, las variables en las colas de las flechas) y los efectos (es decir, las variables en las puntas de las flechas). Esta es una convención común de diagramas de bucles causales en dinámica de sistemas. En tercer lugar, se utilizan líneas más gruesas para identificar los bucles de retroalimentación y los vínculos en los que el autor desea que se centre la audiencia. Esta también es una convención común de diagramas de dinámica de sistemas. Por último, está claro que a un tomador de decisiones le resultaría imposible pensar en el comportamiento dinámico inherente al modelo, a partir de la inspección de la figura únicamente. [15]
Ejemplo: movimiento del pistón
- Objetivo: estudio de un sistema de biela-manivela.
Queremos modelar un sistema de biela-manivela mediante un modelo dinámico de sistemas. Se pueden encontrar dos descripciones completas diferentes del sistema físico con sistemas de ecuaciones relacionados aquí (en inglés) y aquí (en francés) ; dan los mismos resultados. En este ejemplo, la manivela, con radio y frecuencia angular variables, accionará un pistón con una longitud de biela variable. - Modelado dinámico del sistema: el sistema ahora está modelado según una lógica dinámica del sistema de stock y flujo.
La figura siguiente muestra el diagrama de stock y flujo .
Diagrama de flujo y stock del sistema de biela-manivela - Simulación: se puede simular el comportamiento del sistema dinámico biela-manivela.
La siguiente figura es una simulación 3D creada mediante animación procedimental . Las variables del modelo animan todas las partes de esta animación: manivela, radio, frecuencia angular, longitud de la biela y posición del pistón.

Véase también
|
|
|
|
Referencias
- ^ "Proyecto de Dinámica de Sistemas en Educación del MIT (SDEP)".
- ^ abcde Michael J. Radzicki y Robert A. Taylor (2008). "Origen de la dinámica de sistemas: Jay W. Forrester y la historia de la dinámica de sistemas". En: Introducción a la dinámica de sistemas del Departamento de Energía de los Estados Unidos . Consultado el 23 de octubre de 2008.
- ^ Forrester, Jay (1971). Comportamiento contraintuitivo de los sistemas sociales. Technology Review 73(3): 52–68
- ^ Goodwin, RM (1982). Un ciclo de crecimiento. En: Ensayos sobre dinámica económica. Palgrave Macmillan, Londres. [1]
- ^ Di Matteo, M., y Sordi, S. (2015). Goodwin en Siena: economista, filósofo social y artista. Cambridge Journal of Economics, 39(6), 1507–1527. [2]
- ^ Sterman, John D. (2000). Dinámica empresarial: pensamiento y modelado sistémico para un mundo complejo . Boston: McGraw-Hill. ISBN 0-07-231135-5.
- ^ Meadows, Donella. (2008). Pensamiento sistémico: una introducción. Earthscan
- ^ Richardson, GP (1986). "Problemas con diagramas de bucles causales". Syst . Dyn. Rev. 2 (2): 158–170. doi :10.1002/sdr.4260020207.
- ^ Sterman, John D. (2001). "Modelado de dinámica de sistemas: herramientas para el aprendizaje en un mundo complejo". California Management Review . 43 (4): 8–25. doi :10.2307/41166098. JSTOR 41166098. S2CID 4637381.
- ^ FHA Rahim, NN Hawari y NZ Abidin, "Oferta y demanda de arroz en Malasia: un enfoque de dinámica de sistemas", International Journal of Supply Chain and Management, vol. 6, n.º 4, págs. 234-240, 2017.
- ^ Sociedad de dinámica de sistemas
- ^ Repenning, Nelson P. (2001). "Entender la lucha contra incendios en el desarrollo de nuevos productos" (PDF) . The Journal of Product Innovation Management . 18 (5): 285–300. doi :10.1016/S0737-6782(01)00099-6. hdl : 1721.1/3961 .
- ^ Nelson P. Repenning (1999). Dependencia de recursos en los esfuerzos de mejora del desarrollo de productos , MIT Sloan School of Management, Departamento de Gestión de Operaciones/Grupo de Dinámica de Sistemas, diciembre de 1999.
- ^ [3] Minsky - Proyecto del mes de enero de 2014. Entrevista con el equipo de desarrollo de Minsky. Consultado en enero de 2014.
- ^ de Michael J. Radzicki y Robert A. Taylor (2008). "Feedback". En: Introducción a la dinámica de sistemas del Departamento de Energía de los Estados Unidos . Consultado el 23 de octubre de 2008.
Lectura adicional
- Kypuros, Javier (2013). Dinámica de sistemas y control con modelado de grafos de enlaces . Boca Raton: Taylor & Francis. ISBN 978-1466560758.
- Forrester, Jay W. (1961). Dinámica industrial . Pegasus Communications. ISBN 978-1-883823-36-8.
- Forrester, Jay W. (1969). Dinámica urbana . Pegasus Communications. ISBN 978-1-883823-39-9.
- Meadows, Donella H. (1972). Los límites del crecimiento . Nueva York: University Books. ISBN 978-0-87663-165-2.
- Morecroft, John (2007). Modelado estratégico y dinámica empresarial: un enfoque de sistemas de retroalimentación . John Wiley & Sons. ISBN 978-0-470-01286-4.
- Roberts, Edward B. (1978). Aplicaciones gerenciales de la dinámica de sistemas . Cambridge: MIT Press. ISBN 978-0-262-18088-7.
- Randers, Jorgen (1980). Elementos del método de dinámica de sistemas . Cambridge: MIT Press. ISBN 978-0-915299-39-3.
- Senge, Peter (1990). La quinta disciplina . Moneda. ISBN 978-0-385-26095-4.
- Sterman, John D. (2000). Dinámica empresarial: pensamiento y modelado sistémico para un mundo complejo . McGraw Hill. ISBN 978-0-07-231135-8.
Enlaces externos
- Sociedad de dinámica de sistemas
- Estudio preparado para el Departamento de Energía de EE. UU. Introducción a la dinámica de sistemas -
- Dinámica de la isla desierta: "Un estudio comentado de la literatura esencial sobre dinámica de sistemas"
- Mundo verdadero: razonamiento temporal Elaboración universal: software de dinámica de sistemas utilizado para los diagramas de este artículo (gratis)

















