Aritmética ordinal

En el campo matemático de la teoría de conjuntos , la aritmética ordinal describe las tres operaciones habituales con números ordinales : suma , multiplicación y exponenciación . Cada una de ellas puede definirse esencialmente de dos formas diferentes: ya sea construyendo un conjunto explícito bien ordenado que represente el resultado de la operación o utilizando la recursión transfinita . La forma normal de Cantor proporciona una forma estandarizada de escribir ordinales. Además de estas operaciones ordinales habituales, también existen la aritmética "natural" de ordinales y las operaciones con números.

La suma de dos conjuntos bien ordenados S y T es el ordinal que representa la variante del orden lexicográfico con la posición menos significativa primero, en la unión de los productos cartesianos S × {0} y T × {1} . De esta manera, cada elemento de S es menor que cada elemento de T , las comparaciones dentro de S mantienen el orden que ya tienen, y lo mismo para las comparaciones dentro de T .

La definición de adición α + β también se puede dar por recursión transfinita sobre β . Cuando el sumando derecho β = 0 , la adición ordinaria da α + 0 = α para cualquier α . Para β > 0 , el valor de α + β es el ordinal más pequeño estrictamente mayor que la suma de α y δ para todo δ < β . Escribiendo los casos de sucesor y ordinales límite por separado:

• α + 0 = α
• α + S ( β ) = S ( α + β ) , donde S denota lafunción sucesora .
• ${\displaystyle \alpha +\beta =\bigcup _{\delta <\beta }(\alpha +\delta )}$cuando β es un ordinal límite .

La adición ordinal de los números naturales es la misma que la adición estándar. El primer ordinal transfinito es ω , el conjunto de todos los números naturales, seguido de ω + 1 , ω + 2 , etc. El ordinal ω + ω se obtiene con dos copias de los números naturales ordenados de la manera habitual y la segunda copia completamente a la derecha de la primera. Escribiendo 0' < 1' < 2' < ... para la segunda copia, ω + ω se ve así

0 < 1 < 2 < 3 < ... < 0' < 1' < 2' < ...

Esto es diferente de ω porque en ω solo 0 no tiene un predecesor directo mientras que en ω + ω los dos elementos 0 y 0' no tienen predecesores directos.

La adición ordinal, en general, no es conmutativa . Por ejemplo, 3 + ω = ω ya que la relación de orden para 3 + ω es 0 < 1 < 2 < 0' < 1' < 2' < ... , que puede reetiquetarse como ω . Por el contrario, ω + 3 no es igual a ω ya que la relación de orden 0 < 1 < 2 < ... < 0' < 1' < 2' tiene un elemento más grande (a saber, 2' ) y ω no lo tiene ( ω y ω + 3 son equipotentes , pero no isomorfos en orden).

La suma ordinal sigue siendo asociativa ; se puede ver por ejemplo que ( ω + 4) + ω = ω + (4 + ω ) = ω + ω .

La adición es estrictamente creciente y continua en el argumento correcto:

${\displaystyle \alpha <\beta \Rightarrow \gamma +\alpha <\gamma +\beta }$

Pero la relación análoga no se cumple para el argumento izquierdo; en su lugar sólo tenemos:

${\displaystyle \alpha <\beta \Rightarrow \alpha +\gamma \leq \beta +\gamma }$

La adición ordinal es cancelativa por la izquierda : si α + β = α + γ , entonces β = γ . Además, se puede definir la resta por la izquierda para los ordinales β ≤ α : existe un único γ tal que α = β + γ . Por otro lado, la cancelación por la derecha no funciona:

${\displaystyle 3+\omega =0+\omega =\omega }$pero${\estilo de visualización 3\neq 0}$

Tampoco la resta derecha, incluso cuando β ≤ α : por ejemplo, no existe ningún γ tal que γ + 42 = ω .

Si los ordinales menores que α son cerrados bajo adición y contienen 0, entonces α se denomina ocasionalmente un número γ (ver ordinal aditivamente indescomponible ). Estos son exactamente los ordinales de la forma ω ^β .

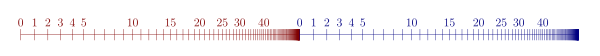
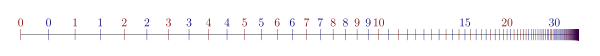
El producto cartesiano , S × T , de dos conjuntos bien ordenados S y T puede ordenarse bien mediante una variante del orden lexicográfico que coloca la posición menos significativa primero. En efecto, cada elemento de T se reemplaza por una copia disjunta de S . El tipo de orden del producto cartesiano es el ordinal que resulta de multiplicar los tipos de orden de S y T .

La definición de multiplicación también se puede dar por recursión transfinita sobre β . Cuando el factor correcto β = 0 , la multiplicación ordinaria da α · 0 = 0 para cualquier α . Para β > 0 , el valor de α · β es el ordinal más pequeño mayor o igual que ( α · δ ) + α para todo δ < β . Escribiendo los casos de sucesor y ordinales límite por separado:

• α · 0 = 0.
• α · S ( β ) = ( α · β ) + α , para un ordinal sucesor S ( β ) .
• ${\displaystyle \alpha \cdot \beta =\bigcup _{\delta <\beta }(\alpha \cdot \delta )}$, cuando β es un ordinal límite.

A modo de ejemplo, aquí está la relación de orden para ω · 2 :

0 ₀ < 1 ₀ < 2 ₀ < 3 ₀ < ... < 0 ₁ < 1 ₁ < 2 ₁ < 3 ₁ < ...,

que tiene el mismo tipo de orden que ω + ω . En cambio, 2 · ω se ve así:

0 ₀ < 1 ₀ < 0 ₁ < 1 ₁ < 0 ₂ < 1 ₂ < 0 ₃ < 1 ₃ < ...

y después de volver a etiquetar, esto se ve como ω . Por lo tanto, ω · 2 = ω + ω ≠ ω = 2 · ω , lo que demuestra que la multiplicación de ordinales no es en general conmutativa, cf imágenes.

Al igual que ocurre con la suma, la multiplicación ordinal de números naturales es lo mismo que la multiplicación estándar.

α · 0 = 0 · α = 0 , y la propiedad del producto cero se cumple: α · β = 0 → α = 0 o β = 0 . El ordinal 1 es una identidad multiplicativa, α · 1 = 1 · α = α . La multiplicación es asociativa, ( α · β ) · γ = α · ( β · γ ) . La multiplicación es estrictamente creciente y continua en el argumento correcto: ( α < β y γ > 0 ) → γ · α < γ · β . La multiplicación no esestrictamente creciente en el argumento de la izquierda, por ejemplo, 1 < 2 sino 1 · ω = 2 · ω = ω . Sin embargo, es (no estrictamente) creciente, es decir, α ≤ β → α · γ ≤ β · γ .

La multiplicación de ordinales no es, en general, conmutativa. En concreto, un número natural mayor que 1 nunca conmuta con ningún ordinal infinito, y dos ordinales infinitos α y β conmutan si y solo si α ^m = β ⁿ para algunos números naturales m y n distintos de cero . La relación " α conmuta con β " es una relación de equivalencia sobre los ordinales mayores que 1, y todas las clases de equivalencia son infinitas contablemente.

La distributividad se cumple, a la izquierda: α ( β + γ ) = αβ + αγ . Sin embargo, la ley distributiva de la derecha ( β + γ ) α = βα + γα generalmente no es cierta: (1 + 1) · ω = 2 · ω = ω mientras que 1 · ω + 1 · ω = ω + ω , que es diferente. Existe una ley de cancelación por la izquierda : si α > 0 y α · β = α · γ , entonces β = γ . La cancelación de derechos no funciona, por ejemplo, 1 · ω = 2 · ω = ω , pero 1 y 2 son diferentes. Una división por la izquierda con propiedad de resto se cumple: para todos los α y β , si β > 0 , entonces hay γ y δ únicos tales que α = β · γ + δ y δ < β . La división por la derecha no funciona: no hay α tal que α · ω ≤ ω ^ω ≤ ( α + 1) · ω .

Los números ordinales forman un semicírculo izquierdo , pero no forman un anillo . Por lo tanto, los ordinales no son un dominio euclidiano , ya que ni siquiera son un anillo; además, la "norma" euclidiana tendría un valor ordinal utilizando la división izquierda en este caso.

Un número δ (véase Ordinal indecomponible multiplicativamente ) es un ordinal β mayor que 1 tal que αβ = β siempre que 0 < α < β . Estos consisten en el ordinal 2 y los ordinales de la forma β = ω ^{ω γ} .

La definición de exponenciación a través de tipos de orden se explica más fácilmente usando la definición de Von Neumann de un ordinal como el conjunto de todos los ordinales más pequeños . Luego, para construir un conjunto de tipo de orden α ^β considere el conjunto de todas las funciones f  : β → α tales que f ( x ) = 0 para todos excepto un número finito de elementos x ∈ β (esencialmente, consideramos las funciones con soporte finito ). Este conjunto está ordenado lexicográficamente con la posición menos significativa primero: escribimos f < g si y solo si existe x ∈ β con f ( x ) < g ( x ) y f ( y ) = g ( y ) para todos los y ∈ β con x < y . Este es un buen ordenamiento y, por lo tanto, da un número ordinal.

La definición de exponenciación también se puede dar por recursión transfinita sobre el exponente β . Cuando el exponente β = 0 , la exponenciación ordinaria da α ⁰ = 1 para cualquier α . Para β > 0 , el valor de α ^β es el ordinal más pequeño mayor o igual que α ^δ · α para todo δ < β . Escribiendo los casos de sucesor y ordinales límite por separado:

• α0 ⁼ 1 .
• α ^{S ( β )} = ( α ^β ) · α , para un ordinal sucesor S ( β ) .
• ${\displaystyle \alpha ^{\beta }=\bigcup _{0<\delta <\beta }(\alpha ^{\delta })}$, cuando β es un ordinal límite.

Ambas definiciones se simplifican considerablemente si el exponente β es un número finito: α ^β es entonces simplemente el producto de β copias de α ; por ejemplo, ω ³ = ω · ω · ω , y los elementos de ω ³ pueden verse como triples de números naturales, ordenados lexicográficamente con la posición menos significativa primero. Esto concuerda con la exponenciación ordinaria de números naturales.

Pero para exponentes infinitos, la definición puede no ser obvia. Por ejemplo, α ^ω se puede identificar con un conjunto de secuencias finitas de elementos de α , correctamente ordenados. La ecuación 2 ^ω = ω expresa el hecho de que las secuencias finitas de ceros y unos se pueden identificar con números naturales, utilizando el sistema numérico binario . El ordinal ω ^ω se puede ver como el tipo de orden de las secuencias finitas de números naturales; cada elemento de ω ^ω (es decir, cada ordinal menor que ω ^ω ) se puede escribir de forma única en la forma donde k , n ₁ , ..., n _k son números naturales, c ₁ , ..., c _k son números naturales distintos de cero, y n ₁ > ... > n _k .${\displaystyle \omega ^{n_{1}}c_{1}+\omega ^{n_{2}}c_{2}+\cdots +\omega ^{n_{k}}c_{k}}$

Lo mismo es cierto en general: cada elemento de α ^β (es decir, cada ordinal menor que α ^β ) se puede escribir de forma única en la forma donde k es un número natural, b ₁ , ..., b _k son ordinales menores que β con b ₁ > ... > b _k , y a ₁ , ..., a _k son ordinales distintos de cero menores que α . Esta expresión corresponde a la función f  : β → α que envía b _i a a _i para i = 1, ..., k y envía todos los demás elementos de β a 0.${\displaystyle \alpha ^{b_{1}}a_{1}+\alpha ^{b_{2}}a_{2}+\cdots +\alpha ^{b_{k}}a_{k}}$

Si bien se utiliza la misma notación de exponente para la exponenciación ordinal y la exponenciación cardinal , las dos operaciones son bastante diferentes y no deben confundirse. La exponenciación cardinal A ^B se define como el número cardinal del conjunto de todas las funciones B → A , mientras que la exponenciación ordinal α ^β solo contiene las funciones β → α con soporte finito, típicamente un conjunto de cardinalidad mucho menor. Para evitar confundir la exponenciación ordinal con la exponenciación cardinal, se pueden usar símbolos para ordinales (p. ej . ω ) en la primera y símbolos para cardinales (p. ej. ) en la segunda.$estilo de visualización {\aleph _{0}}$

• α0 ⁼ 1 .
• Si 0 < α , entonces 0 ^α = 0 .
• 1α ⁼ 1 .
• α1 = α .^​
• αβ · αγ = αβ ^{+ γ} .^​​​
• ( αβ ) ^γ = αβ ^{· γ} .^​​
• Hay α , β y γ para los cuales ( α · β ) ^γ ≠ α ^γ · β ^γ . Por ejemplo, ( ω · 2) ² = ω ·2 · ω ·2 = ω ² · 2 ≠ ω ² · 4 .
• La exponenciación ordinal es estrictamente creciente y continua en el argumento derecho: si γ > 1 y α < β , entonces γ ^α < γ ^β .
• Si α < β , entonces α ^γ ≤ β ^γ . Tenga en cuenta, por ejemplo, que 2 < 3 y, sin embargo, 2 ^ω = 3 ^ω = ω .
• Si α > 1 y α ^β = α ^γ , entonces β = γ . Si α = 1 o α = 0 este no es el caso.
• Para todos α y β , si β > 1 y α > 0 entonces existen γ , δ y ρ únicos tales que α = β ^γ · δ + ρ tales que 0 < δ < β y ρ < β ^γ .

Jacobsthal demostró que las únicas soluciones de α ^β = β ^α con α ≤ β están dadas por α = β , o α = 2 y β = 4 , o α es cualquier límite ordinal y β = εα donde ε es un número ε mayor que α . ^[1]

Existen operaciones ordinales que continúan la secuencia iniciada con la suma, la multiplicación y la exponenciación, incluidas las versiones ordinales de tetración , pentación y hexación . Véase también función de Veblen .

Cada número ordinal α puede escribirse de forma única como , donde k es un número natural, son números naturales distintos de cero y son números ordinales. El caso degenerado α = 0 ocurre cuando k = 0 y no hay β ni c . Esta descomposición de α se denomina forma normal de Cantor de α y puede considerarse el sistema de numeración posicional de base ω . El exponente más alto se denomina grado de y satisface . La igualdad se aplica si y solo si . En ese caso, la forma normal de Cantor no expresa el ordinal en términos de los más pequeños; esto puede suceder como se explica a continuación.${\displaystyle \omega ^{\beta _{1}}c_{1}+\omega ^{\beta _{2}}c_{2}+\cdots +\omega ^{\beta _{k}}c_{k}}$${\displaystyle c_{1},c_{2},\ldots ,c_{k}}$${\displaystyle \beta _ {1}>\beta _ {2}>\ldots >\beta _ {k}\geq 0}$ $estilo de visualización {\beta _{1}}$${\estilo de visualización \alpha}$${\displaystyle \beta _{1}\leq \alpha }$${\displaystyle \beta _ {1}=\alpha}$${\displaystyle \alpha =\omega ^{\alpha }}$

Una pequeña variación de la forma normal de Cantor, que suele ser un poco más sencilla de manejar, consiste en hacer que todos los números c _i sean iguales a 1 y permitir que los exponentes sean iguales. En otras palabras, cada número ordinal α se puede escribir de forma única como , donde k es un número natural y son números ordinales.${\displaystyle \omega ^{\beta _{1}}+\omega ^{\beta _{2}}+\cdots +\omega ^{\beta _{k}}}$${\displaystyle \beta _{1}\geq \beta _{2}\geq \ldots \geq \beta _{k}\geq 0}$

Otra variación de la forma normal de Cantor es la "expansión de base δ ", donde ω se reemplaza por cualquier ordinal δ > 1 , y los números c _i son ordinales distintos de cero menores que δ .

La forma normal de Cantor nos permite expresar de forma única -y ordenar- los ordinales α que se construyen a partir de los números naturales mediante un número finito de operaciones aritméticas de adición, multiplicación y exponenciación base- : en otras palabras, suponiendo en la forma normal de Cantor, también podemos expresar los exponentes en forma normal de Cantor, y haciendo la misma suposición para los que para α y así sucesivamente de forma recursiva, obtenemos un sistema de notación para estos ordinales (por ejemplo,${\displaystyle \omega }$${\displaystyle \beta _{1}<\alpha }$${\displaystyle \beta _{i}}$${\displaystyle \beta _{i}}$

${\displaystyle \omega ^{\omega ^{\omega ^{7}\cdot 6+\omega +42}\cdot 1729+\omega ^{9}+88}\cdot 3+\omega ^{\omega ^{\omega }}\cdot 5+65537}$

denota un ordinal).

El ordinal ε ₀ ( épsilon cero ) es el conjunto de valores ordinales α de las expresiones aritméticas de longitud finita de la forma normal de Cantor que son hereditariamente no triviales donde no trivial significa β ₁ ​​< α cuando 0 < α . Es el ordinal más pequeño que no tiene una expresión aritmética finita en términos de ω , y el ordinal más pequeño tal que , es decir, en la forma normal de Cantor el exponente no es menor que el ordinal mismo. Es el límite de la secuencia${\displaystyle \varepsilon _{0}=\omega ^{\varepsilon _{0}}}$

${\displaystyle 0,\,1=\omega ^{0},\,\omega =\omega ^{1},\,\omega ^{\omega },\,\omega ^{\omega ^{\omega }},\,\ldots \,.}$

El ordinal ε ₀ es importante por varias razones en aritmética (esencialmente porque mide la fuerza de la teoría de la demostración de la aritmética de Peano de primer orden : es decir, los axiomas de Peano pueden mostrar inducción transfinita hasta cualquier ordinal menor que ε ₀ pero no hasta ε ₀ mismo).

La forma normal de Cantor también nos permite calcular sumas y productos de ordinales: para calcular la suma, por ejemplo, uno sólo necesita saber (ver las propiedades enumeradas en § Adición y § Multiplicación) que

${\displaystyle \omega ^{\beta }c+\omega ^{\beta '}c'=\omega ^{\beta '}c'\,,}$

si (si se puede aplicar la ley distributiva a la izquierda y reescribir esto como , y si la expresión ya está en forma normal de Cantor); y para calcular productos, los hechos esenciales son que cuando está en forma normal de Cantor y , entonces${\displaystyle \beta '>\beta }$${\displaystyle \beta '=\beta }$${\displaystyle \omega ^{\beta }(c+c')}$${\displaystyle \beta '<\beta }$${\displaystyle 0<\alpha =\omega ^{\beta _{1}}c_{1}+\cdots +\omega ^{\beta _{k}}c_{k}}$${\displaystyle 0<\beta '}$

${\displaystyle \alpha \omega ^{\beta '}=\omega ^{\beta _{1}+\beta '}\,}$

y

${\displaystyle \alpha n=\omega ^{\beta _{1}}c_{1}n+\omega ^{\beta _{2}}c_{2}+\cdots +\omega ^{\beta _{k}}c_{k}\,,}$

si n es un número natural distinto de cero.

Para comparar dos ordinales escritos en forma normal de Cantor, primero compare , luego , luego , luego , y así sucesivamente. En la primera aparición de la desigualdad, el ordinal que tiene el componente más grande es el ordinal más grande. Si son iguales hasta que uno termina antes que el otro, entonces el que termina primero es más pequeño.${\displaystyle \beta _{1}}$${\displaystyle c_{1}}$${\displaystyle \beta _{2}}$${\displaystyle c_{2}}$

Ernst Jacobsthal demostró que los ordinales satisfacen una forma del teorema de factorización única: todo ordinal distinto de cero puede escribirse como producto de un número finito de ordinales primos. Esta factorización en ordinales primos no es, en general, única, pero existe una factorización "mínima" en primos que es única hasta que se cambia el orden de los factores primos finitos (Sierpiński 1958).

Un ordinal primo es un ordinal mayor que 1 que no se puede escribir como producto de dos ordinales menores. Algunos de los primeros primos son 2, 3, 5, ... , ω , ω + 1 , ω ² + 1 , ω ³ + 1 , ..., ω ^ω , ω ^ω + 1 , ω ^{ω + 1} + 1 , ... Hay tres tipos de ordinales primos:

• Los primos finitos 2, 3, 5, ...
• Los ordinales de la forma ω ^{ω α} para cualquier ordinal α . Estos son los ordinales primos que son límites, y son los números delta , los ordinales transfinitos que son cerrados bajo la multiplicación.
• Los ordinales de la forma ω ^α + 1 para cualquier ordinal α > 0. Estos son los primos sucesores infinitos, y son los sucesores de los números gamma , los ordinales aditivamente indescomponibles.

La factorización en primos no es única: por ejemplo, 2×3 = 3×2 , 2× ω = ω , ( ω +1)× ω = ω × ω y ω × ω ^ω = ω ^ω . Sin embargo, existe una factorización única en primos que satisface las siguientes condiciones adicionales:

• Todo primo límite debe ocurrir antes de cualquier primo sucesor.
• Si dos primos consecutivos de la factorización prima son ambos límites o ambos finitos, el segundo debe ser menor o igual que el primero.

Esta factorización prima se puede leer fácilmente utilizando la forma normal de Cantor de la siguiente manera:

• Primero escribe el ordinal como un producto αβ donde α es la potencia más pequeña de ω en la forma normal de Cantor y β es un sucesor.
• Si α = ω ^γ entonces escribir γ en forma normal de Cantor da una expansión de α como producto de primos límite.
• Ahora observemos la forma normal de Cantor de β . Si β = ω ^λ m + ω ^μ n + términos más pequeños, entonces β = ( ω ^μ n + términos más pequeños)( ω ^{λ − μ} + 1) m es un producto de un ordinal más pequeño y un primo y un número natural m . Repitiendo esto y factorizando los números naturales en primos obtenemos la factorización prima de β .

Así que la factorización del ordinal de la forma normal de Cantor

ω ^{α ₁} n ₁ + ⋯ + ω ^{α _k} n _k (con α ₁ > ⋯ > α _k )

en un producto mínimo de infinitos números primos y naturales es

( ω ^{ω β ₁} ⋯ ω ^{ω β _m} ) n _k ( ω ^{α _{k −1} −α _k} + 1) n _{k −1} ⋯ ( ω ^{α ₁ − α ₂} + 1) n ₁

donde cada n _i debe reemplazarse por su factorización en una secuencia no creciente de primos finitos y

α _k = ω ^{β ₁} + ⋯ + ω ^{β _m} con β ₁ ≥ ⋯ ≥ β _m .

Como se ha comentado anteriormente, la forma normal de Cantor de los ordinales inferiores a ε ₀ se puede expresar en un alfabeto que contenga únicamente los símbolos de función para la adición, la multiplicación y la exponenciación, así como símbolos constantes para cada número natural y para ω . Podemos prescindir de los infinitos numerales utilizando únicamente el símbolo constante 0 y la operación de sucesor, S (por ejemplo, el número natural 4 se puede expresar como S(S(S(S(0))))). Esto describe una notación ordinal : un sistema para nombrar ordinales en un alfabeto finito. Este sistema particular de notación ordinal se denomina la colección de expresiones ordinales aritméticas , y puede expresar todos los ordinales inferiores a ε ₀ , pero no puede expresar ε ₀ . Existen otras notaciones ordinales capaces de capturar ordinales mucho más allá de ε ₀ , pero como solo hay un número contable de cadenas de longitud finita en cualquier alfabeto finito, para cualquier notación ordinal dada habrá ordinales por debajo de ω ₁ (el primer ordinal incontable ) que no sean expresables. Dichos ordinales se conocen como ordinales contables grandes .

Las operaciones de suma, multiplicación y exponenciación son ejemplos de funciones ordinales recursivas primitivas , y se pueden usar funciones ordinales recursivas primitivas más generales para describir ordinales más grandes.

Las operaciones de suma natural y producto natural sobre ordinales fueron definidas en 1906 por Gerhard Hessenberg y a veces se denominan suma (o producto) de Hessenberg (Sierpiński 1958). La suma natural de α y β se suele denotar por α ⊕ β o α # β , y el producto natural por α ⊗ β o α ⨳ β .

La suma y el producto naturales se definen de la siguiente manera. Sean y en forma normal de Cantor (es decir, y ). Sean los exponentes ordenados en orden no creciente. Entonces se define como El producto natural de y se define como Por ejemplo, supongamos que y . Entonces , mientras que . Y , mientras que .${\displaystyle \alpha =\omega ^{\alpha _{1}}+\cdots +\omega ^{\alpha _{k}}}$${\displaystyle \beta =\omega ^{\beta _{1}}+\cdots +\omega ^{\beta _{\ell }}}$${\displaystyle \alpha _{1}\geq \cdots \geq \alpha _{k}}$${\displaystyle \beta _{1}\geq \cdots \geq \beta _{\ell }}$${\displaystyle \gamma _{1},\ldots ,\gamma _{k+\ell }}$${\displaystyle \alpha _{1},\ldots ,\alpha _{k},\beta _{1},\ldots ,\beta _{\ell }}$${\displaystyle \alpha \oplus \beta }$$${\displaystyle \alpha \oplus \beta =\omega ^{\gamma _{1}}+\cdots +\omega ^{\gamma _{k+\ell }}.}$$${\displaystyle \alpha }$${\displaystyle \beta }$$${\displaystyle \alpha \otimes \beta =\bigoplus _{\begin{aligned}&1\leq i\leq k\\&1\leq j\leq \ell \end{aligned}}\omega ^{\alpha _{i}\oplus \beta _{j}}.}$$${\displaystyle \alpha =\omega ^{\omega ^{\omega }}+\omega }$${\displaystyle \beta =\omega ^{\omega }+\omega ^{5}}$${\displaystyle \alpha \oplus \beta =\omega ^{\omega ^{\omega }}+\omega ^{\omega }+\omega ^{5}+\omega }$${\displaystyle \alpha +\beta =\omega ^{\omega ^{\omega }}+\omega ^{\omega }+\omega ^{5}}$${\displaystyle \alpha \otimes \beta =\omega ^{\omega ^{\omega }+\omega }+\omega ^{\omega ^{\omega }+5}+\omega ^{\omega +1}+\omega ^{6}}$${\displaystyle \alpha \beta =\omega ^{\omega ^{\omega }+\omega }+\omega ^{\omega ^{\omega }+5}}$

La suma y el producto naturales son conmutativos y asociativos, y el producto natural se distribuye sobre la suma natural. Las operaciones también son monótonas, en el sentido de que si entonces ; si entonces ; y si y entonces .${\displaystyle \alpha <\beta }$${\displaystyle \alpha \oplus \gamma <\beta \oplus \gamma }$${\displaystyle \alpha \leq \beta }$${\displaystyle \alpha \otimes \gamma \leq \beta \otimes \gamma }$${\displaystyle \alpha <\beta }$${\displaystyle \gamma >0}$${\displaystyle \alpha \otimes \gamma <\beta \otimes \gamma }$

Tenemos .${\displaystyle \underbrace {\alpha \oplus \cdots \oplus \alpha } _{n}=\alpha \otimes n}$

Siempre tenemos y . Si ambos y entonces . Si ambos y entonces .${\displaystyle \alpha +\beta \leq \alpha \oplus \beta }$${\displaystyle \alpha \beta \leq \alpha \otimes \beta }$${\displaystyle \alpha <\omega ^{\gamma }}$${\displaystyle \beta <\omega ^{\gamma }}$${\displaystyle \alpha \oplus \beta <\omega ^{\gamma }}$${\displaystyle \alpha <\omega ^{\omega ^{\gamma }}}$${\displaystyle \beta <\omega ^{\omega ^{\gamma }}}$${\displaystyle \alpha \otimes \beta <\omega ^{\omega ^{\gamma }}}$

La suma y el producto naturales no son continuos en el argumento correcto, ya que, por ejemplo , y no ; y , y no .${\displaystyle \lim _{n<\omega }\alpha \oplus n=\alpha +\omega }$${\displaystyle \alpha \oplus \omega }$${\displaystyle \lim _{n<\omega }\alpha \otimes n=\alpha \omega }$${\displaystyle \alpha \otimes \omega }$

La suma y el producto naturales son lo mismo que la adición y la multiplicación (restringidas a los ordinales) del campo de números surrealistas de John Conway .

Las operaciones naturales aparecen en la teoría de los órdenes parciales bien definidos ; dados dos órdenes parciales bien definidos y , de tipos ( linealizaciones máximas ) y , el tipo de la unión disjunta es , mientras que el tipo del producto directo es . ^[2] Se puede tomar esta relación como una definición de las operaciones naturales eligiendo S y T como ordinales α y β ; por lo que α ⊕ β es el tipo de orden máximo de un orden total que extiende la unión disjunta (como un orden parcial) de α y β ; mientras que α ⊗ β es el tipo de orden máximo de un orden total que extiende el producto directo (como un orden parcial) de α y β . ^[3] Una aplicación útil de esto es cuando α y β son ambos subconjuntos de un orden total mayor; entonces su unión tiene un tipo de orden como máximo α ⊕ β . Si ambos son subconjuntos de algún grupo abeliano ordenado , entonces su suma tiene como máximo tipo de orden α ⊗ β .${\displaystyle S}$${\displaystyle T}$${\displaystyle o(S)}$${\displaystyle o(T)}$${\displaystyle o(S)\oplus o(T)}$${\displaystyle o(S)\otimes o(T)}$

También podemos definir la suma natural α ⊕ β por recursión transfinita simultánea sobre α y β , como el ordinal más pequeño estrictamente mayor que la suma natural de α y γ para todo γ < β y de γ y β para todo γ < α . ^[4] De manera similar, podemos definir el producto natural α ⊗ β por recursión transfinita simultánea sobre α y β , como el ordinal más pequeño γ tal que ( α ⊗ δ ) ⊕ ( ε ⊗ β ) < γ ⊕ ( ε ⊗ δ ) para todo ε < α y δ < β . ^[4] Además, véase el artículo sobre números surrealistas para la definición de multiplicación natural en ese contexto; sin embargo, utiliza la resta surrealista, que no está definida en ordinales.

La suma natural es asociativa y conmutativa. Siempre es mayor o igual que la suma usual, pero puede ser estrictamente mayor. Por ejemplo, la suma natural de ω y 1 es ω + 1 (la suma usual), pero esta es también la suma natural de 1 y  ω . El producto natural es asociativo y conmutativo y se distribuye sobre la suma natural. El producto natural es siempre mayor o igual que el producto usual, pero puede ser estrictamente mayor. Por ejemplo, el producto natural de ω y 2 es ω · 2 (el producto usual), pero este es también el producto natural de 2 y  ω .

Bajo la adición natural, los ordinales pueden identificarse con los elementos del monoide conmutativo libre generado por los números gamma ω ^α . Bajo la adición y multiplicación naturales, los ordinales pueden identificarse con los elementos del semianillo conmutativo libre generado por los números delta ω ^{ω α} . Los ordinales no tienen factorización única en primos bajo el producto natural. Mientras que el anillo polinomial completo tiene factorización única, el subconjunto de polinomios con coeficientes no negativos no la tiene: por ejemplo, si x es cualquier número delta, entonces

x ⁵ + x ⁴ + x ³ + x ² + x + 1 = ( x + 1) ( x ⁴ + x ² + 1) = ( x ² + x + 1) ( x ³ + 1)

tiene dos expresiones incompatibles como producto natural de polinomios con coeficientes no negativos que no se pueden descomponer más.

Existen operaciones aritméticas con ordinales en virtud de la correspondencia uno a uno entre ordinales y nimbers . Tres operaciones comunes con nimbers son la suma de nimbers, la multiplicación de nimbers y la exclusión mínima (mex) . La suma de nimbers es una generalización de la operación exclusiva bit a bit o con números naturales. El mex de un conjunto de ordinales es el ordinal más pequeño que no está presente en el conjunto.

• Calculadora ordinal ordCalc