Paralelo (operador)

El operador paralelo (pronunciado "paralelo", [1] siguiendo la notación de líneas paralelas de la geometría ; [2] [3] también conocido como suma reducida , suma paralela o adición paralela ) es una operación binaria que se utiliza como abreviatura en ingeniería eléctrica , [4] [5] [6] [nb 1] pero también se utiliza en cinética , mecánica de fluidos y matemáticas financieras . [7] [8] El nombre paralelo proviene del uso del operador que calcula la resistencia combinada de resistencias en paralelo .
Descripción general
El operador paralelo representa el valor recíproco de una suma de valores recíprocos (a veces también denominado "fórmula recíproca" o " suma armónica ") y se define por: [9] [6] [10] [11]
donde a , b y son elementos de los números complejos extendidos [12] [13]
El operador da la mitad de la media armónica de dos números a y b . [7] [8]
Como caso especial, para cualquier número :
Además, para todos los números distintos :
representando el valor absoluto de , y significando el mínimo (menor elemento) entre x e y .
Si y son números reales positivos distintos entonces
El concepto se ha extendido desde una operación escalar a matrices [14] [15] [16] [17] [18] y se ha generalizado aún más . [19]
Notación
El operador fue introducido originalmente como suma reducida por Sundaram Seshu en 1956, [20] [21] [14] estudiado como operador ∗por Kent E. Erickson en 1959, [22] [23] [14] y popularizado por Richard James Duffin y William Niles Anderson, Jr. como operador de suma paralela u operador de suma paralela: en matemáticas y teoría de redes desde 1966. [15] [16] [1] Si bien algunos autores continúan usando este símbolo hasta el presente, [7] [8] por ejemplo, Sujit Kumar Mitra lo usó ∙como símbolo en 1970. [14] En electrónica aplicada , un ∥signo se volvió más común como símbolo del operador alrededor de 1974. [24] [25] [26] [27] [28] [nb 1] [nb 2] Esto a menudo se escribía como una línea vertical doble (||) disponible en la mayoría de los conjuntos de caracteres (a veces en cursiva como //[29] [30] ), pero ahora se puede representar utilizando el carácter Unicode U+2225 ( ∥ ) para "paralelo a". En LaTeX y lenguajes de marcado relacionados, las macros \|y \parallelse utilizan a menudo (y rara vez \smallparallelse utilizan) para indicar el símbolo del operador.
Propiedades
Sea el plano complejo extendido excluyendo el cero, y la función biyectiva de a tal que Uno tiene identidades
y
Esto implica inmediatamente que es un campo donde el operador paralelo toma el lugar de la adición, y que este campo es isomorfo a
Las siguientes propiedades se pueden obtener traduciendo las propiedades correspondientes de los números complejos.
Propiedades del campo
Como ocurre con cualquier campo, satisface una variedad de identidades básicas.
Es conmutativa bajo paralelo y multiplicación:
Es asociativa bajo paralelismo y multiplicación: [12] [7] [8]
Ambas operaciones tienen un elemento identidad ; para la paralela la identidad es mientras que para la multiplicación la identidad es 1 :
Cada elemento de tiene un inverso en paralelo, igual al inverso aditivo en la adición. (Pero 0 no tiene inverso en paralelo).
El elemento identidad es su propio inverso,
Cada elemento de tiene un inverso multiplicativo :
La multiplicación es distributiva sobre paralela: [1] [7] [8]
Paralelo repetido
El paralelo repetido es equivalente a la división,
O bien, multiplicando ambos lados por n ,
A diferencia de la suma repetida , esto no conmuta:
Expansión binomial
Utilizando la propiedad distributiva dos veces, el producto de dos binomios paralelos se puede desarrollar como
El cuadrado de un binomio es
El cubo de un binomio es
En general, la potencia n de un binomio se puede desarrollar utilizando coeficientes binomiales que son el recíproco de los de la suma, lo que da como resultado un análogo de la fórmula binomial :
Logaritmo y exponencial
Se cumplen las siguientes identidades:
Factorización de polinomios paralelos
Al igual que con un polinomio bajo adición, un polinomio paralelo con coeficientes en (con ) se puede factorizar en un producto de monomios:
para algunas raíces (posiblemente repetidas) en
Análoga a los polinomios bajo adición, la ecuación polinómica
implica que para algún k .
Fórmula cuadrática
Una ecuación lineal se puede resolver fácilmente mediante la inversa paralela:
Para resolver una ecuación cuadrática paralela, complete el cuadrado para obtener un análogo de la fórmula cuadrática.
Incluyendo cero
Los números complejos extendidos , incluido el cero, ya no son un cuerpo en operaciones paralelas y de multiplicación, porque el 0 no tiene inverso en operaciones paralelas. (Esto es análogo a la forma en que no es un cuerpo porque no tiene inverso aditivo).
Para cada a distinto de cero ,
La cantidad puede dejarse indefinida (ver forma indeterminada ) o definirse como igual a 0 .
Precedencia
En ausencia de paréntesis, el operador paralelo se define como que tiene prioridad sobre la suma o la resta, de forma similar a la multiplicación. [1] [31] [9] [10]
Aplicaciones
Existen aplicaciones del operador paralelo en electrónica, óptica y estudio de la periodicidad:
Análisis de circuitos
En ingeniería eléctrica , el operador paralelo se puede utilizar para calcular la impedancia total de varios circuitos eléctricos en serie y en paralelo . [nb 2] Existe una dualidad entre la suma habitual (en serie) y la suma en paralelo. [7] [8]
Por ejemplo, la resistencia total de las resistencias conectadas en paralelo es el recíproco de la suma de los recíprocos de las resistencias individuales .
Lo mismo ocurre con la capacitancia total de los capacitores en serie . [nb 2]
Ecuación de la lente
En óptica geométrica, la aproximación de la lente delgada a la ecuación del fabricante de lentes.
Periodo sinódico
El tiempo transcurrido entre las conjunciones de dos cuerpos en órbita se denomina período sinódico . Si el período del cuerpo más lento es T 2 y el del más rápido es T 1 , entonces el período sinódico es
Ejemplos
Pregunta:
- Tres resistencias y están conectadas en paralelo . ¿Cuál es su resistencia resultante?
Respuesta:
- La resistencia efectivamente resultante es de aproximadamente 57 k Ω .
Pregunta: [7] [8]
- Un trabajador de la construcción levanta un muro en 5 horas. Otro trabajador necesitaría 7 horas para realizar el mismo trabajo. ¿Cuánto tiempo se tarda en levantar el muro si ambos trabajadores trabajan en paralelo?
Respuesta:
- Terminarán en cerca de 3 horas.
Implementación

Sugerido ya por Kent E. Erickson como una subrutina en computadoras digitales en 1959, [22] el operador paralelo se implementa como un operador de teclado en las calculadoras científicas de Notación Polaca Inversa (RPN) WP 34S desde 2008 [32] [33] [34] así como en la WP 34C [35] y WP 43S desde 2015, [36] [37] permitiendo resolver incluso problemas en cascada con pocas pulsaciones de teclas como .270↵ Enter180∥120∥
Visión proyectiva
Dado un cuerpo F hay dos incrustaciones de F en la línea proyectiva P( F ): z → [ z : 1] y z → [1 : z ]. Estas incrustaciones se superponen excepto para [0:1] y [1:0]. El operador paralelo relaciona la operación de adición entre las incrustaciones. De hecho, las homografías en la línea proyectiva están representadas por matrices de 2 x 2 M(2, F ), y las operaciones de cuerpo (+ y ×) se extienden a las homografías. Cada incrustación tiene su adición a + b representada por las siguientes multiplicaciones de matrices en M(2, A ):
Los dos productos matriciales muestran que hay dos subgrupos de M(2, F ) isomorfos a ( F ,+), el grupo aditivo de F . Dependiendo de qué incrustación se utilice, una operación es +, la otra es
Notas
- ^ ab Si bien el uso del símbolo ∥ para "paralelo" en geometría se remonta a 1673 en la obra de John Kersey el mayor , [A] este comenzó a usarse más a partir de aproximadamente 1875. [B] El uso de un operador matemático para circuitos paralelos se origina en la teoría de redes en ingeniería eléctrica . Sundaram Seshu introdujo un operador de suma reducida en 1956, [C] Kent E. Erickson propuso un asterisco (∗) para simbolizar el operador en 1959, [D] mientras que Richard James Duffin y William Niles Anderson, Jr. usaron dos puntos (:) para la adición paralela desde 1966. [E] Sujit Kumar Mitra usó un punto medio (∙) para ello en 1970. [F] Se desconoce el primer uso del símbolo paralelo (∥) para este operador en electrónica aplicada , pero podría haberse originado en el libro de Stephen D. Senturia y Bruce D. Wedlock de 1974 "Electronic Circuits and Applications", [G] que evolucionó a partir de su curso introductorio de electrónica en el Instituto Tecnológico de Massachusetts (MIT) con conceptos de enseñanza de teoría de redes y electrónica derivados de un curso anterior impartido por Campbell "Cam" Leach Searle. Se popularizó aún más a través del libro de John W. McWane de 1981 "Introducción a la electrónica y la instrumentación", [H] que surgió de un curso del MIT con el mismo nombre desarrollado como parte del influyente Proyecto de Desarrollo del Currículo Técnico entre 1974 y 1979. Este símbolo probablemente también se introdujo porque los otros símbolos utilizados podían confundirse fácilmente con los signos comúnmente utilizados para la multiplicación y la división en algunos contextos.
- ^ abc En circuitos eléctricos el operador paralelo puede aplicarse, respectivamente, a resistencias paralelas ( R en [Ω]) o inductancias ( L en [H]) así como a impedancias ( Z en [Ω]) o reactancias ( X en [Ω]). Ignorando el glifo del símbolo del operador, que en ese momento puede resultar engañoso , también puede aplicarse a circuitos en serie de, respectivamente, conductancias ( G en [S]) o capacitancias ( C en [F]) así como a admitancias ( Y en [S]) o susceptancias ( B en [S]).
Referencias
- ^ abcd Duffin, Richard James (1971) [1970, 1969]. "Network Models". Escrito en Durham, Carolina del Norte, EE. UU. En Wilf, Herbert Saul ; Hararay, Frank (eds.). Mathematical Aspects of Electrical Network Analysis. Actas de un simposio sobre matemáticas aplicadas de la American Mathematical Society y la Society for Industrial and Applied Mathematics celebrado en la ciudad de Nueva York, 1969-04-02/03. Vol. III de las Actas SIAM-AMS (edición ilustrada). Providence, Rhode Island: American Mathematical Society (AMS) / Society for Industrial and Applied Mathematics (SIAM). págs. 65–92 [68]. ISBN 0-8218-1322-6. ISSN 0080-5084. LCCN 79-167683. ISBN 978-0-8218-1322-5 . Informe 69-21 . Consultado el 5 de agosto de 2019 . págs. 68–69:
[…] Para tener una notación corta conveniente para la resistencia conjunta de resistencias conectadas en paralelo, sea […] A:B = AB/(A+B) […] A:B puede considerarse como una nueva operación denominada
adición en paralelo
[…] La adición en paralelo se define para cualquier número no negativo. El modelo de red muestra que la adición en paralelo es
conmutativa
y
asociativa
. Además, la multiplicación es
distributiva
sobre esta operación. Consideremos ahora una expresión algebraica en las operaciones (+) y (:) que operan sobre números positivos A, B, C, etc. […] Para dar una interpretación de red de dicho polinomio, léase
A + B
como "A serie B" y
A : B
como "A paralelo B", entonces es claro que la expresión […] es la resistencia conjunta de la red […]
[1] [2] (206 páginas)
- ^ Kersey (el mayor), John (1673). "Capítulo I: Sobre el alcance de este cuarto libro y el significado de los caracteres, abreviaturas y citas que se utilizan en él". Los elementos de ese arte matemático, comúnmente llamado álgebra. Vol. Libro IV - Los elementos de las artes algebraicas. Londres: Thomas Passinger, Three-Bibles, London-Bridge. págs. 177–178. Archivado desde el original el 2020-08-05 . Consultado el 2019-08-09 .
- ^ Cajori, Florian (1993) [septiembre de 1928]. "§ 184, § 359, § 368". Una historia de las notaciones matemáticas: notaciones en matemáticas elementales. Vol. 1 (dos volúmenes en una sola edición reimpresa sin modificaciones). Chicago, EE. UU.: Open Court Publishing Company . págs. 193, 402–403, 411–412. ISBN 0-486-67766-4. LCCN 93-29211 . Consultado el 22 de julio de 2019 . págs. 402–403, 411–412:
§359. […] ∥ para paralelo aparece en la Opuscula mathematica hactenus inedita (1677) de Oughtred [p. 197], una obra póstuma (§ 184) […] §368. Signos para líneas paralelas. […] cuando el signo de igualdad de Recorde se abrió camino en el continente , las líneas verticales comenzaron a usarse para el paralelismo. Encontramos ∥ para "paralelo" en Kersey , [A] Caswell , Jones , [B] Wilson, [C] Emerson , [D] Kambly, [E] y los escritores de los últimos cincuenta años que ya han sido citados en relación con otros pictogramas. Antes de 1875 aproximadamente no aparecía con tanta frecuencia […] Hall y Stevens [F] usan "par [F] o ∥" para paralelo […] [A] John Kersey , Álgebra (Londres, 1673), Libro IV, pág. 177.[B] W. Jones , Sinopsis palmarioum matheseos (Londres, 1706).[C] John Wilson, Trigonometría (Edimburgo, 1714), caracteres explicados.[D] W. Emerson , Elementos de geometría (Londres, 1763), pág. 4.[E] L. Kambly , Die Elementar-Mathematik , Parte 2: Planimetrie , 43. edición (Breslau, 1876), p. 8. […][F] HS Hall y FH Stevens, Elementos de Euclides , Partes I y II (Londres, 1889), pág. 10. […]
[3] - ^ "INA 326/INA 327 – Amplificador de instrumentación de E/S de precisión de riel a riel" (PDF) . Burr-Brown / Texas Instruments . 2018 [noviembre de 2004, noviembre de 2001]. págs. 3, 9, 13. SBOS222D. Archivado (PDF) desde el original el 2019-07-13 . Consultado el 2019-07-13 .
- ^ Bober, William; Stevens, Andrew (2016). "Capítulo 7.6. Transformadas de Laplace aplicadas a circuitos". Métodos numéricos y analíticos con MATLAB para ingenieros eléctricos. Mecánica aplicada y computacional (1.ª ed.). CRC Press . p. 224. ISBN 978-1-46657607-0. ISBN 1-46657607-3 . (388 páginas)
- ^ ab Ranade, Gireeja; Stojanovic, Vladimir, eds. (otoño de 2018). "Capítulo 15.7.2 Resistencias paralelas" (PDF) . EECS 16A Diseño de dispositivos y sistemas de información I (PDF) (notas de clase). Universidad de California, Berkeley . p. 12. Nota 15. Archivado (PDF) desde el original el 27 de diciembre de 2018 . Consultado el 28 de diciembre de 2018 . p. 12:
[…] Esta relación matemática surge con tanta frecuencia que en realidad tiene un nombre: el "operador paralelo", denotado ∥. Cuando decimos x∥y, significa
. Nótese que este es un operador matemático y no dice nada sobre la configuración real. En el caso de las resistencias, el operador paralelo se usa para resistencias paralelas, pero para otros componentes (como los capacitores) este
no
es el caso. […]
(16 páginas)
- ^ abcdefg Ellerman, David Patterson (21 de marzo de 1995). "Capítulo 12: Adición paralela, dualidad serie-paralelo y matemáticas financieras". La intrusión intelectual como forma de vida: ensayos de filosofía, economía y matemáticas (PDF) . La filosofía mundana: estudios en la intersección de la filosofía y la economía (edición ilustrada). Rowman & Littlefield Publishers, Inc., págs. 237-268. ISBN 0-8476-7932-2. Archivado (PDF) del original el 5 de marzo de 2016 . Consultado el 9 de agosto de 2019 . p. 237:
[…] Cuando se colocan en serie resistencias con resistencia a y b, su resistencia compuesta es la suma habitual (en adelante, suma en serie ) de las resistencias a + b. Si las resistencias se colocan en paralelo, su resistencia compuesta es la suma en paralelo de las resistencias, que se denota con los dos puntos […]
[4] (271 páginas) - ^ abcdefg Ellerman, David Patterson (mayo de 2004) [21 de marzo de 1995]. "Introducción a la dualidad serie-paralelo" (PDF) . Universidad de California en Riverside . CiteSeerX 10.1.1.90.3666 . Archivado desde el original el 10 de agosto de 2019 . Consultado el 9 de agosto de 2019 .
La suma paralela de dos números reales positivos x:y = [(1/x) + (1/y)]
−1
surge en la teoría de circuitos eléctricos como la resistencia resultante de conectar dos resistencias x e y en paralelo. Existe una
dualidad
entre la
suma habitual (en serie)
y la suma paralela. […]
[5] (24 páginas)
- ^ ab Basso, Christophe P. (2016). "Capítulo 1.1.2 El divisor de corriente". Funciones de transferencia de circuitos lineales: Introducción a las técnicas analíticas rápidas (1.ª ed.). Chichester, West Sussex, Nueva Jersey, EE. UU.: John Wiley & Sons Ltd. pág. 12. ISBN 978-1-11923637-5. LCCN 2015047967 . Consultado el 28 de diciembre de 2018 .(464 páginas)
- ^ ab Cotter, Neil E., ed. (2015-10-12) [2014-09-20]. "ECE1250 Cookbook – Nodes, Series, Parallel" (notas de clase). Libros de cocina. Universidad de Utah . Archivado (PDF) desde el original el 2020-08-20 . Consultado el 2019-08-11 .
[…] Una forma conveniente de indicar que dos resistencias están en paralelo es poner un ∥ entre ellas. […]
- ^ Böcker, Joachim (18 de marzo de 2019) [abril de 2008]. "Grundlagen der Elektrotechnik Teil B" (PDF) (en alemán). Universidad de Paderborn . pag. 12. Archivado (PDF) desde el original el 17 de abril de 2018 . Consultado el 9 de agosto de 2019 . pag. 12:
Für die Berechnung des Ersatzwiderstands der Parallelschaltung wird […] gern die Kurzschreibweise ∥ benutzt.
- ^ ab Georg, Otfried (2013) [1999]. "Capítulo 2.11.4.3: Aufstellen der Differentialgleichung aus der komplexen Darstellung - MATHCAD Anwendung 2.11-6: Benutzerdefinierte Operadores". Elektromagnetische Felder und Netzwerke: Anwendungen in Mathcad und PSpice. Springer-Lehrbuch (en alemán) (1 ed.). Springer-Verlag . págs. 246-248. doi :10.1007/978-3-642-58420-6. ISBN 978-3-642-58420-6. ISBN 3-642-58420-9 . Consultado el 4 de agosto de 2019 . (728 páginas)
- ^
 Álgebra de composición asociativa/Homografías en Wikilibros
Álgebra de composición asociativa/Homografías en Wikilibros - ^ abcd Mitra, Sujit Kumar (febrero de 1970). "Una operación matricial para analizar multipuertos en serie y en paralelo". Journal of the Franklin Institute . Brief Communication. 289 (2). Franklin Institute : 167–169. doi :10.1016/0016-0032(70)90302-9. p. 167:
El propósito de esta comunicación es extender el concepto de la operación
escalar
Suma reducida introducida por Seshu […] y posteriormente elaborada por Erickson […] a matrices, para esbozar algunas propiedades interesantes de esta nueva operación matricial y aplicar la operación matricial en el análisis de
redes
de n
puertos en serie y en paralelo. Sean A y B dos matrices cuadradas
no singulares
que tienen
inversas
, A
−1
y B
−1
respectivamente. Definimos la operación ∙ como A ∙ B = (A
−1
+ B
−1
)
−1
y la operación ⊙ como A ⊙ B = A ∙ (−B). La operación ∙ es
conmutativa
y
asociativa
y también es
distributiva
respecto de la multiplicación. […]
(3 páginas)
- ^ ab Duffin, Richard James ; Hazony, Dov; Morrison, Norman Alexander (marzo de 1966) [1965-04-12, 1964-08-25]. "Síntesis de redes a través de matrices híbridas". Revista SIAM de Matemáticas Aplicadas . 14 (2). Sociedad de Matemáticas Industriales y Aplicadas (SIAM): 390–413. doi :10.1137/0114032. JSTOR 2946272.(24 páginas)
- ^ ab Anderson, Jr., William Niles; Duffin, Richard James (1969) [1968-05-27]. "Suma de matrices en serie y en paralelo". Journal of Mathematical Analysis and Applications . 26 (3). Academic Press, Inc. : 576–594. doi : 10.1016/0022-247X(69)90200-5 . p. 576:
[…] definimos la suma paralela de A y B por la fórmula A(A + B)
+
B y la denotamos por A : B. Si A y B no son singulares esto se reduce a A : B = (A
−1
+ B
−1
)
−1
que es la fórmula eléctrica bien conocida para la suma de resistencias en paralelo. Luego se muestra que las
matrices semidefinidas
hermíticas forman un semigrupo
conmutativo
parcialmente ordenado bajo la operación de suma paralela. […]
[6]
- ^ Mitra, Sujit Kumar; Puri, Madan Lal (octubre de 1973). "Sobre la suma y diferencia paralelas de matrices" (PDF) . Revista de análisis matemático y aplicaciones . 44 (1). Academic Press, Inc. : 92–97. doi :10.1016/0022-247X(73)90027-9. Archivado desde el original (PDF) el 13 de abril de 2019.
- ^ Mitra, Sujit Kumar; Bhimasankaram, Pochiraju; Malik, Saroj B. (2010). Órdenes parciales de matrices, operadores acortados y aplicaciones. Series in Algebra. Vol. 10 (1.ª ed. ilustrada). World Scientific Publishing Co. Pte. Ltd. ISBN 978-981-283-844-5. ISBN 981-283-844-9 . Consultado el 19 de agosto de 2019 . (446 páginas)
- ^ Eriksson-Bique, Sirkka-Liisa Anneli [en finlandés] ; Leutwiler, Heinz (febrero de 1989) [10 de enero de 1989]. "Una generalización de la suma paralela" (PDF) . Aecuaciones Mathematicae . 38 (1). Birkhäuser Verlag : 99-110. doi :10.1007/BF01839498. Archivado (PDF) desde el original el 2020-08-20 . Consultado el 20 de agosto de 2020 .
- ^ Seshu, Sundaram (septiembre de 1956). "Sobre circuitos eléctricos y circuitos de conmutación". IRE Transactions on Circuit Theory . CT-3 (3). Instituto de Ingenieros de Radio (IRE): 172–178. doi :10.1109/TCT.1956.1086310.(7 páginas) (NB. Ver erratas.)
- ^ Seshu, Sundaram; Gould, Roderick (septiembre de 1957). "Corrección de 'Sobre circuitos eléctricos y circuitos de conmutación'". IRE Transactions on Circuit Theory . Corrección. CT-4 (3). Instituto de Ingenieros de Radio (IRE): 284. doi : 10.1109/TCT.1957.1086390 .(1 página) (NB. Se refiere a la referencia anterior.)
- ^ ab Erickson, Kent E. (marzo de 1959). "Una nueva operación para analizar redes en serie-paralelo". IRE Transactions on Circuit Theory . CT-6 (1). Institute of Radio Engineers (IRE): 124–126. doi :10.1109/TCT.1959.1086519. pág. 124:
[…] La operación ∗ se define como A ∗ B = AB/A + B. El símbolo ∗ tiene propiedades algebraicas que simplifican la solución formal de muchos problemas de redes en serie-paralelo. Si la operación ∗ se incluyera como una subrutina en una
computadora digital
, podría simplificar la programación de ciertos cálculos de red. […]
(3 páginas) (NB. Ver comentario.)
- ^ Kaufman, Howard (junio de 1963). "Observación sobre una nueva operación para analizar redes en serie y en paralelo". IEEE Transactions on Circuit Theory . CT-10 (2). Institute of Electrical and Electronics Engineers (IEEE): 283. doi :10.1109/TCT.1963.1082126. p. 283:
[…] Comentarios sobre la operación ∗ […] a∗b = ab/(a+b) […]
(1 página) (NB. Se refiere a la referencia anterior.) - ^ Senturia, Stephen D. [en Wikidata] ; Wedlock, Bruce D. (1975) [agosto de 1974]. "Parte A. Aprendizaje del lenguaje, Capítulo 3. Redes resistivas lineales, 3.2 Configuraciones básicas de red, 3.2.3. Resistencias en paralelo". Escrito en el Instituto Tecnológico de Massachusetts, Cambridge, Massachusetts, EE. UU. Circuitos electrónicos y aplicaciones (1.ª ed.). Nueva York, Londres, Sídney, Toronto: John Wiley & Sons, Inc. pp. viii–ix, 44–46 [45]. ISBN 0-471-77630-0. LCCN 74-7404. S2CID 61070327. pp. viii, ix, 45:
Este libro de texto evolucionó a partir de un curso introductorio de electrónica de un semestre impartido por los autores en el Instituto Tecnológico de Massachusetts . […] El curso es utilizado por muchos estudiantes de primer año como precursor del Programa Básico de Ingeniería Eléctrica del MIT. […] La preparación de un libro de este tamaño se ha basado en la contribución de muchas personas. El concepto de enseñar la teoría de redes y la electrónica como un solo tema unificado deriva del profesor Campbell Searle, quien enseñó el curso introductorio de electrónica cuando uno de nosotros (SDS) era un estudiante de posgrado de física de primer año que intentaba aprender electrónica. Además, el profesor Searle ha proporcionado una crítica constructiva invaluable a lo largo de la redacción de este texto. Varios miembros de la facultad del MIT y casi 40 asistentes técnicos graduados han participado en la enseñanza de este material durante los últimos cinco años, muchos de los cuales han hecho contribuciones importantes a través de sus sugerencias y ejemplos. Entre ellos, queremos agradecer especialmente a OR Mitchell, Irvin Englander, George Lewis, Ernest Vincent, David James, Kenway Wong, Gim Hom, Tom Davis, James Kirtley y Robert Donaghey. El presidente del Departamento de Ingeniería Eléctrica del MIT, el profesor Louis D. Smullin , ha proporcionado apoyo y estímulo durante este proyecto, al igual que muchos colegas de todo el departamento. […] El primer resultado […] establece que el voltaje total a través de la combinación en paralelo de R 1 y R 2 es el mismo que el que se produce a través de una única resistencia de valor R 1 R 2 (R 1 + R 2 ). Debido a que esta expresión para la resistencia en paralelo ocurre tan a menudo, se le da una notación especial (R 1 ∥R 2 ). Es decir, cuando R 1 y R 2 están en paralelo, la resistencia equivalente es […]
(xii+623+5 páginas) (NB: También estaba disponible un manual para el profesor. Las primeras tiradas contienen una cantidad considerable de errores tipográficos. Véase también: el libro de Wedlock de 1978.) [7] - ^ Wolf, Lawrence J. (1977) [1976, 1974]. "Sección 4. Materiales didácticos – 4.3. Proyecto de desarrollo del currículo técnico del MIT – Introducción a la electrónica y la instrumentación". En Aldridge, Bill G.; Mowery, Donald R.; Wolf, Lawrence J.; Dixon, Peggy (eds.). Tecnología científica e ingeniería – Guía curricular: una guía para un currículo de grado asociado de dos años (PDF) . Saint Louis Community College–Florissant Valley , St. Louis, Missouri, EE. UU.: National Science Teachers Association , Washington DC, EE. UU. pp. 21, 77. Archivado (PDF) desde el original el 2017-02-15 . Consultado el 2019-08-08 . p. 21:
[…] Introducción a la electrónica y la instrumentación es un enfoque nuevo y contemporáneo para el curso introductorio de electrónica. Diseñado para estudiantes sin experiencia previa en electrónica, desarrolla las habilidades y conocimientos necesarios para utilizar y comprender los sistemas electrónicos modernos. […] John W. McWane […]
(NB. El Proyecto SET fue un programa de estudios postsecundarios de dos años desarrollado entre 1974 y 1977 para preparar a los técnicos para utilizar instrumentos electrónicos). - ^ Wiesner, Jerome Bert ; Johnson, Howard Wesley ; Killian, Jr., James Rhyne , eds. (1978-04-11). "Escuela de Ingeniería – Centro de Estudios Avanzados de Ingeniería (CAES) – Investigación y Desarrollo – Proyecto de Investigación y Desarrollo del Currículo Técnico". Informe del Presidente y el Canciller 1977–78 – Instituto Tecnológico de Massachusetts (PDF) . Instituto Tecnológico de Massachusetts (MIT). págs. 249, 252–253. Archivado (PDF) desde el original el 2015-09-10 . Consultado el 2019-08-08 . págs. 249, 252–253:
[…] El Programa de Investigación y Desarrollo del Currículo Técnico, patrocinado por la Organización Imperial de Servicios Sociales
de
Irán
, está entrando en el cuarto año de un contrato de cinco años. Continúa el desarrollo del currículo en electrónica e ingeniería mecánica. […] Administrado conjuntamente por
CAES
y el
Departamento de Ciencia e Ingeniería de Materiales
, el Proyecto está bajo la supervisión del Profesor Merton C. Flemings. Está dirigido por el Dr. John W. McWane. […] Desarrollo de materiales curriculares. Esta es la actividad principal del proyecto y se ocupa del desarrollo de materiales de cursos innovadores y de última generación en áreas necesarias de tecnología de ingeniería […] nuevo curso introductorio en electrónica […] se titula Introducción a la electrónica y la instrumentación y consta de ocho […] módulos […] Corriente continua, voltaje y resistencia; Redes de circuitos básicos; Señales variables en el tiempo; Amplificadores operacionales; Fuentes de alimentación; Corriente alterna, voltaje e impedancia; Circuitos digitales; y Medición y control electrónicos. Este curso representa un cambio importante y una actualización de la forma en que se introduce la electrónica, y debería ser de gran valor para
STI,
así como para muchos programas de EE. UU. […]
- ^ Wedlock, Bruce D. (1978). Redes de circuitos básicos . Introducción a la electrónica y la instrumentación. Instituto Tecnológico de Massachusetts (MIT), Proyecto de investigación y desarrollo de currículo técnico.(81 páginas) (NB: Esto formó la base de la Parte I del libro de McWane de 1981. Véase también: el libro de Senturia y Wedlock de 1975).
- ^ McWane, John W. (1 de mayo de 1981). Introducción a la electrónica y la instrumentación (edición ilustrada). North Scituate, Massachusetts, EE. UU.: Breton Publishers , Wadsworth, Inc., págs. 78, 96–98, 100, 104. ISBN 0-53400938-7. ISBN 978-0-53400938-0 . Consultado el 4 de agosto de 2019 . p. xiii, 96–98, 100:
[…] Bruce D. Wedlock […] fue el principal autor colaborador de la Parte I, REDES DE CIRCUITOS BÁSICOS, incluido el diseño de los ejemplos complementarios. […] La mayor parte del desarrollo del programa IEI se llevó a cabo como parte del Proyecto de investigación y desarrollo del currículo técnico del
Centro de estudios de ingeniería avanzada del MIT
. […] notación abreviada […] símbolo abreviado ∥ […]
(xiii+545 páginas) (NB: En 1981, también existía un manual de laboratorio de 216 páginas que acompañaba a este libro. El trabajo surgió de un programa de curso del MIT "The MIT Technical Curriculum Development Project - Introduction to Electronics and Instrumentation" desarrollado entre 1974 y 1979. En 1986, se publicó una segunda edición de este libro bajo el título "Introducción a la tecnología electrónica".)
- ^ "7.5.3 Selección de la resistencia externa". Temporizador de sistema nano-potente TPL5110 para control de potencia (PDF) (Hoja de datos). Revisión A. Texas Instruments Incorporated . Septiembre de 2018 [enero de 2015]. págs. 13-14. SNAS650A. Archivado (PDF) desde el original el 25 de septiembre de 2022. Consultado el 25 de septiembre de 2022 .(27 páginas)
- ^ "A7987: Regulador reductor de conmutación asíncrono de 61 V, 3 A con limitación de corriente ajustable para automoción" (PDF) (Hoja de datos). Revisión 3. STMicroelectronics NV . 2020-09-22 [2019-03-19]. págs. 17, 18, 20. DS12928. Archivado (PDF) desde el original el 2022-07-18 . Consultado el 2022-07-18 .(36 páginas)
- ^ Pablo, Steffen; Paul, Reinhold (24 de octubre de 2014). "Capítulo 2.3.2: Zusammenschaltungen resistivo lineal Zweipole - Parallelschaltung". Grundlagen der Elektrotechnik und Elektronik 1: Gleichstromnetzwerke und ihre Anwendungen (en alemán). vol. 1 (5 ed.). Springer-Verlag . pag. 78.ISBN 978-3-64253948-0. ISBN 3-64253948-3 . Consultado el 4 de agosto de 2019 . pag. 78:
[…] Bei abgekürzter Schreibweise achte man sorgfältig auf die Anwendung von Klammern. […] Das Parallelzeichen ∥ der Kurzschreibweise hat die gleiche Bedeutung wie ein Multiplikationszeichen. Deshalb können Klammern entfallen.
(446 páginas) - ^ Dale, Paul; Bonin, Walter (2012-11-30) [2008-12-09]. Manual del propietario del WP 34S (PDF) (3.1 ed.). págs. 1, 14, 32, 66, 116. Archivado (PDF) desde el original el 2019-07-09 . Consultado el 2019-07-13 .[8] (211 páginas)
- ^ Bonin, Walter (2015) [9 de diciembre de 2008]. Manual del propietario de WP 34S (3.3.ª edición). CreateSpace Independent Publishing Platform . ISBN 978-1-5078-9107-0.[9]
- ^ Bonin, Walter (11 de julio de 2016) [9 de diciembre de 2008]. Manual del propietario de WP 34S (4.ª edición). CreateSpace Independent Publishing Platform . ISBN 978-1-53366238-5. ISBN 1-53366238-X . (410 páginas)
- ^ Dowrick, Nigel (3 de mayo de 2015) [16 de marzo de 2015]. "Modo de bloqueo complejo para WP-34". Museo HP . Archivado desde el original el 3 de abril de 2019. Consultado el 7 de agosto de 2019 .
- ^ Bonin, Walter (2020) [2015]. Manual del propietario del WP 43S (PDF) . 0.16 (edición preliminar). pág. 119. ISBN 978-1-72950098-9. ISBN 1-72950098-6 . Archivado (PDF) del original el 21 de julio de 2022 . Consultado el 20 de agosto de 2020 . [10] [11] (328 páginas)
- ^ Bonin, Walter (2020) [2015]. Manual de referencia WP 43S (PDF) . 0.16 (edición preliminar). pág. 127. ISBN 978-1-72950106-1. ISBN 1-72950106-0 . Archivado (PDF) desde el original el 21 de julio de 2022 . Consultado el 20 de agosto de 2020 . [12] [13] (315 páginas)
Lectura adicional
- Pekarev, Èdward L.; Šmul'jan, Ju. L. (30 de abril de 1976). "Suma paralela y resta paralela de operadores". Matemáticas de la URSS-Izvestia . 10 (2). Sociedad Matemática Americana : 351–370. Código Bibliográfico :1976IzMat..10..351P. doi :10.1070/IM1976v010n02ABEH001694.
- Duffin, Richard James ; Morley, Tom D. (julio de 1978). "Operadores casi definidos y sistemas electromecánicos". Revista SIAM de Matemáticas Aplicadas . 35 (1). Sociedad de Matemáticas Industriales y Aplicadas (SIAM): 21–30. doi :10.1137/0135003. JSTOR 2101028.(10 páginas)
- Morley, Tom D. (julio de 1979). "Suma paralela, principio de Maxwell y el ínfimo de las proyecciones" (PDF) . Journal of Mathematical Analysis and Applications . 70 (1). Departamento de Matemáticas, Universidad de Illinois en Urbana-Champaign , Urbana, Illinois, EE. UU.: 33–41. doi :10.1016/0022-247X(79)90073-8. Archivado desde el original el 20 de agosto de 2020 . Consultado el 20 de agosto de 2020 .
- Seeger, Alberto (mayo de 1990) [1988-03-22]. "Suma directa e inversa en análisis convexo y aplicaciones" (PDF) . Journal of Mathematical Analysis and Applications . 148 (2). Departamento de Matemáticas, Universidad de Washington , Seattle, Washington, EE. UU.: Academic Press, Inc. : 317–349. doi :10.1016/0022-247X(90)90004-Y. Archivado (PDF) desde el original el 20 de agosto de 2020 . Consultado el 20 de agosto de 2020 .(33 páginas)
- Bryant, Randal E .; Tygar, J. Doug; Huang, Lawrence P. (1994). "Caracterización geométrica de redes de resistencias variables en serie-paralelo" (PDF) . IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications . 41 (11): 686–698. doi :10.1109/81.331520. Archivado desde el original (PDF) el 14 de agosto de 2017.
- Antezana, Jorge; Corach, Gustavo; Stojanoff, Demetrio (abril de 2006) [2005-09-14]. "Operadores bilaterales en corto y sumas paralelas" (PDF) . Álgebra lineal y sus aplicaciones . 414 (2–3). La Plata, Argentina y Buenos Aires, Argentina: 570–588. arXiv : math/0509327 . doi :10.1016/j.laa.2005.10.039. Archivado (PDF) desde el original el 2017-08-09 . Consultado el 2020-08-20 .[14] (19 páginas)
- Chansangiam, Pattrawut (febrero de 2016) [agosto de 2015, julio de 2015]. "Aspectos matemáticos para conexiones de redes eléctricas". Revista de ingeniería de la KKU . 43 (1): 47–54. doi :10.14456/kkuenj.2016.8. Archivado (PDF) desde el original el 20 de agosto de 2020. Consultado el 20 de agosto de 2020 .
- Besenyei, Ádám (1 de septiembre de 2016). "La irresistible desigualdad de Milne" (PDF) . Budapest: Departamento de Análisis Aplicado y Matemática Computacional, Universidad Eötvös Loránd . CIA2016. Archivado (PDF) desde el original el 8 de agosto de 2019 . Consultado el 11 de agosto de 2019 .
- "7.5 Características eléctricas: VCC = 5 V / 7.6 Características eléctricas: VCC = 2,7 V / 9.1.2.1 Comparador inversor con histéresis". TLV3201, TLV3202: Comparadores de salida Push-Pull, microPOWER, TLV320x de 40 ns (PDF) . Revisión B. Dallas, Texas, EE. UU.: Texas Instruments Incorporated . 2022-06-03 [2016, 2012]. págs. 5, 6, 13–14 [13]. SBOS561B. Archivado (PDF) desde el original el 2022-08-17 . Consultado el 2022-08-18 . p. 5:
PARÁMETRO […] TIPO […] UNIDAD […] IMPEDANCIA DE ENTRADA […] Modo común […] 10 13 ∥ 2 […] Ω ∥ pF […] Diferencial […] 10 13 ∥ 4 […] Ω ∥ pF […]
(37 páginas) (NB: Uso inusual de ∥ tanto para valores como para unidades).
Enlaces externos
- https://github.com/microsoftarchive/edx-platform-1/blob/master/common/lib/calc/calc/calc.py























![{\displaystyle {\begin{aligned}a\paralelo b&=b\paralelo a\\[3mu]ab&=ba\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33fdcf548e5e335be871903cc2d0cc02147439db)













![{\displaystyle {\begin{aligned}(a\paralelo b)(c\paralelo d)&=a(c\paralelo d)\paralelo b(c\paralelo d)\\[3mu]&=ac\paralelo ad\paralelo bc\paralelo bd.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75796fff00982215ddf28125ac13967f56303ac6)
![{\displaystyle {\begin{aligned}(a\paralelo b)^{2}&=a^{2}\paralelo ab\paralelo ba\paralelo b^{2}\\[3mu]&=a^{2}\paralelo {\tfrac {1}{2}}ab\paralelo b^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cc365e2090c31a9a827d434b9def70074105726)












![{\displaystyle {\begin{aligned}ax\paralelo b&=\infty \\[3mu]\implies x&=-{\frac {b}{a}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f17b63944689d920e5fe583a2faa06bad488bc9)
![{\displaystyle {\begin{aligned}ax^{2}\paralelo bx\paralelo c&=\infty \\[5mu]x^{2}\paralelo {\frac {b}{a}}x&=-{\frac {c}{a}}\\[5mu]x^{2}\paralelo {\frac {b}{a}}x\paralelo {\frac {4b^{2}}{a^{2}}}&=\left(-{\frac {c}{a}}\right)\paralelo {\frac {4b^{2}}{a^{2}}}\\[5mu]\left(x\paralelo {\frac {2b}{a}}\right)^{2}&={\frac {b^{2}\paralelo -{\tfrac {1}{4}}ac}{{\tfrac {1}{4}}a^{2}}}\\[5mu]\implies x&={\frac {(-b)\paralelo \pm {\sqrt {b^{2}\paralelo -{\tfrac {1}{4}}ac}}}{{\tfrac {1}{2}}a}}.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499ed1736b0e0cf7cea1e6de3291ffaacb848cfe)




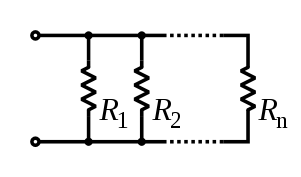
![{\displaystyle {\begin{aligned}{\frac {1}{R_{\text{eq}}}}&={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}\\[5mu]R_{\text{eq}}&=R_{1}\paralelo R_{2}\paralelo \cdots \paralelo R_{n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92fddb4b991c03b156b12dd85c3cca8c3a3f66c1)





![{\displaystyle {\begin{aligned}R_{1}\parallel R_{2}\parallel R_{3}&=270\,\mathrm {k\Omega } \parallel 180\,\mathrm {k\Omega } \ paralelo 120\,\mathrm {k\Omega } \\[5mu]&={\frac {1}{{\dfrac {1}{270\,\mathrm {k\Omega } }}+{\dfrac {1}{180\,\mathrm {k\Omega } }}+{\dfrac {1}{120\,\mathrm { k\Omega } }}}}\\[5mu]&\aproximadamente 56,84\,\mathrm {k\Omega } \end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8635ca3fd9bb42d8a264124fe968db472bb0486d)

![{\displaystyle {\begin{alineado}{\begin{pmatrix}1&0\\a&1\end{pmatrix}}{\begin{pmatrix}1&0\\b&1\end{pmatrix}}&={\begin{pmatrix}1&0\\a+b&1\end{pmatrix}},\\[10mu]{\begin{pmatrix}1&a\\0&1\end{pmatrix}}{\begin{pmatrix}1&b\\0&1\end{pmatrix}}&={\begin{pmatrix}1&a+b\\0&1\end{pmatrix}}.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a775bf62a63081caef53f3f33667ce290bbc4f5)



