Fecha de Pascua

Como fiesta movible , [1] [2] la fecha de la Pascua se determina cada año a través de un cálculo conocido como computus ( en latín , "computación"). [3] La Pascua se celebra el primer domingo después de la luna llena pascual (una aproximación matemática de la primera luna llena astronómica , el 21 de marzo o después, en sí misma una aproximación fija del equinoccio de marzo ). Determinar esta fecha de antemano requiere una correlación entre los meses lunares y el año solar , teniendo en cuenta también el mes, la fecha y el día de la semana del calendario juliano o gregoriano . [4] La complejidad del algoritmo surge debido al deseo de asociar la fecha de Pascua con la fecha de la fiesta judía de la Pascua que, según creen los cristianos, es cuando Jesús fue crucificado. [5]
En un principio, era posible que toda la Iglesia cristiana recibiera la fecha de Pascua cada año mediante un anuncio anual del Papa . Sin embargo, a principios del siglo III, las comunicaciones en el Imperio romano se habían deteriorado hasta el punto de que la Iglesia valoraba mucho un sistema que permitiera al clero determinar la fecha por sí mismo, de forma independiente pero coherente. [6] Además, la Iglesia deseaba eliminar las dependencias del calendario hebreo , derivando la fecha de Pascua directamente del equinoccio de marzo. [7]
En El cálculo del tiempo (725), Beda utiliza computus como un término general para cualquier tipo de cálculo, aunque se refiere a los ciclos de Pascua de Teófilo como un " computus pascual ". A finales del siglo VIII, computus pasó a referirse específicamente al cálculo del tiempo. [8] Los cálculos producen resultados diferentes según se utilice el calendario juliano o el gregoriano. Por esta razón, la Iglesia católica y las iglesias protestantes (que siguen el calendario gregoriano) celebran la Pascua en una fecha diferente a la de la ortodoxia oriental y oriental (que siguen el calendario juliano). Fue la desviación del 21 de marzo respecto del equinoccio observado lo que llevó a la reforma gregoriana del calendario , para volver a alinearlos.
Fondo
La Pascua conmemora la resurrección de Jesús , que los cristianos creen que ocurrió el tercer día (inclusive) después del comienzo de la Pascua . En el calendario lunisolar hebreo , la Pascua comienza al anochecer del día 14 de Nisán . [9] [10] Nisán es el primer mes de primavera en el hemisferio norte , y el día 14 corresponde a una luna llena. Para el siglo II, muchos cristianos habían optado por observar la Pascua solo en domingo. [11] El calendario hebreo no tiene una relación simple con los calendarios cristianos : se resincroniza con el año solar intercalando un mes bisiesto cada dos o tres años, antes del año nuevo lunar el 1 de Nisán . Más tarde, los judíos adoptaron el ciclo metónico para predecir futuras intercalaciones .
Una posible consecuencia de esta intercalación es que el 14 de Nisán podría ocurrir antes del equinoccio, lo que algunos cristianos del siglo III consideraban inaceptable (esto no puede suceder en el calendario fijo que se usa hoy). [12] En consecuencia, se decidió separar la datación de la Pascua del calendario hebreo, identificando la primera luna llena después del equinoccio de marzo. Para la época del Primer Concilio de Nicea (325 d. C.), la Iglesia de Alejandría había designado el 21 de marzo como fecha eclesiástica para el equinoccio, independientemente de la observación astronómica real. En 395, Teófilo publicó una tabla de fechas futuras para la Pascua, validando los criterios alejandrinos. [13] A partir de entonces, el computus sería el procedimiento para determinar el primer domingo después de la primera luna llena eclesiástica que cayera el 21 de marzo o después.
Historia
Las primeras tablas romanas conocidas fueron ideadas en el año 222 por Hipólito de Roma basándose en ciclos de ocho años. Luego, hacia fines del siglo III, Augustalis introdujo en Roma tablas de 84 años. [a] Aunque el obispo Anatolio de Laodicea propuso por primera vez un proceso basado en el ciclo metónico de 19 años alrededor del año 277, el concepto no se afianzó por completo hasta que el método alejandrino cobró autoridad a fines del siglo IV. [b]
El cómputo alejandrino fue convertido del calendario alejandrino al calendario juliano en Alejandría alrededor de 440, lo que dio como resultado una tabla pascual (atribuida al papa Cirilo de Alejandría ) que abarca los años 437 a 531. [16] Esta tabla pascual fue la fuente que inspiró a Dionisio el Exiguo , que trabajó en Roma desde aproximadamente 500 hasta aproximadamente 540, [17] para construir una continuación de ella en la forma de su famosa tabla pascual que abarca los años 532 a 616. [18] Dionisio introdujo la Era Cristiana (contando los años desde la Encarnación de Cristo) al publicar esta nueva tabla de Pascua en 525. [19] [c]
En la primera mitad del siglo IV se adoptó en Roma un ciclo modificado de 84 años. Victorio de Aquitania intentó adaptar el método alejandrino a las reglas romanas en el año 457 en forma de una tabla de 532 años, pero introdujo graves errores. [20] Estas tablas victorianas se utilizaron en la Galia (hoy Francia) y España hasta que fueron sustituidas por las tablas dionisíacas a finales del siglo VIII.
Las tablas de Dionisio y Victorio entraban en conflicto con las que se utilizaban tradicionalmente en las Islas Británicas. Las tablas británicas utilizaban un ciclo de 84 años, pero un error hizo que las lunas llenas cayeran progresivamente demasiado pronto. [21] La discrepancia dio lugar a un informe de que la reina Eanflæd , según el sistema dionisíaco, ayunó el Domingo de Ramos mientras que su marido Oswiu , rey de Northumbria, festejó el Domingo de Pascua. [22]
Como resultado del Sínodo irlandés de Magh-Lene en 630, los irlandeses del sur comenzaron a utilizar las tablas dionisíacas, [23] y los ingleses del norte siguieron su ejemplo después del Sínodo de Whitby en 664. [24]
El cómputo dionisíaco fue descrito en detalle por Beda en 725. [25] Es posible que Carlomagno lo haya adoptado para la Iglesia franca ya en 782 de la mano de Alcuino , un seguidor de Beda. El cómputo dionisíaco/bediano se mantuvo en uso en Europa occidental hasta la reforma del calendario gregoriano, y sigue utilizándose en la mayoría de las iglesias orientales, incluida la gran mayoría de las iglesias ortodoxas orientales y las iglesias no calcedonias . [26] La única iglesia ortodoxa oriental que no sigue el sistema es la iglesia ortodoxa finlandesa, que utiliza el gregoriano.
Habiéndose desviado de los alejandrinos durante el siglo VI, las iglesias más allá de la frontera oriental del antiguo Imperio bizantino, incluida la Iglesia Asiria de Oriente , [27] ahora celebran la Pascua en fechas diferentes a las de las Iglesias Ortodoxas Orientales cuatro veces cada 532 años. [ cita requerida ]
Aparte de estas iglesias en los márgenes orientales del imperio romano, hacia el siglo X todas habían adoptado la Pascua alejandrina, que todavía situaba el equinoccio de primavera en el 21 de marzo, aunque Beda ya había notado su desviación en 725; se había desviado aún más hacia el siglo XVI. [d] Peor aún, la Luna calculada que se utilizó para calcular la Pascua estaba fijada al año juliano por el ciclo de 19 años. Esa aproximación generaba un error de un día cada 310 años, por lo que hacia el siglo XVI el calendario lunar estaba desfasado con respecto a la Luna real por cuatro días. La Pascua gregoriana ha sido utilizada desde 1583 por la Iglesia Católica Romana y fue adoptada por la mayoría de las iglesias protestantes entre 1753 y 1845.
Los estados protestantes alemanes utilizaron una Pascua astronómica entre 1700 y 1776, basada en las Tablas Rudolfinas de Johannes Kepler , que a su vez se basaban en las posiciones astronómicas del Sol y la Luna observadas por Tycho Brahe en su observatorio de Uraniborg en la isla de Ven , mientras que Suecia la utilizó desde 1739 hasta 1844. Esta Pascua astronómica era el domingo después del instante de luna llena que estaba después del instante del equinoccio de primavera usando el tiempo de Uraniborg ( TT + 51 m ) . Sin embargo, se retrasaba una semana si ese domingo era la fecha judía del 15 de Nisán, el primer día de la semana de Pascua, calculada según los métodos judíos modernos. [29]
Esta regla del 15 de Nisán afectó a dos años suecos, 1778 y 1798, que en lugar de ser una semana antes de la Pascua gregoriana, se retrasaron una semana para que coincidieran en domingo con la Pascua gregoriana. La Pascua astronómica de Alemania fue una semana antes de la Pascua gregoriana en 1724 y 1744. [29] La Pascua astronómica de Suecia fue una semana antes de la Pascua gregoriana en 1744, pero una semana después de ella en 1805, 1811, 1818, 1825 y 1829. [29]
Se propusieron dos Pascuas astronómicas modernas, pero ninguna Iglesia las utilizó. La primera fue propuesta como parte del calendario juliano revisado en un Sínodo en Constantinopla en 1923 y la segunda fue propuesta por una Consulta del Consejo Mundial de Iglesias en Alepo en 1997. Ambas usaban la misma regla que las versiones alemana y sueca, pero usaban cálculos astronómicos modernos y la hora de Jerusalén ( TT + 2 h 21 m ) sin la regla del 15 de Nisán. La versión de 1923 habría colocado la Pascua astronómica un mes antes de la Pascua gregoriana en 1924, 1943 y 1962, pero una semana después en 1927, 1954 y 1967. [30] La versión de 1997 habría colocado la Pascua astronómica en el mismo domingo que la Pascua gregoriana para 2000-2025, excepto para 2019, cuando habría sido un mes antes. [31]
Teoría
El ciclo de Pascua agrupa los días en meses lunares, que tienen una duración de 29 o 30 días. Hay una excepción. El mes que termina en marzo normalmente tiene 30 días, pero si el 29 de febrero de un año bisiesto cae dentro de él, contiene 31. Como estos grupos se basan en el ciclo lunar , a largo plazo el mes promedio en el calendario lunar es una muy buena aproximación del mes sinódico , que es29.530 59 días de duración. [32]
El año lunar consta de 12 meses sinódicos, que suman un total de 354 o 355 días. El año lunar es unos 11 días más corto que el año calendario, que tiene una duración de 365 o 366 días. Estos días en los que el año solar supera al año lunar se denominan epactos ( griego : ἐπακταὶ ἡμέραι , translit. épaktai hēmérai , lit. "días intercalares"). [33] [34]
Es necesario añadirlos al día del año solar para obtener el día correcto del año lunar. Siempre que la epacta alcance o supere el número 30, se debe insertar un mes intercalar adicional (o mes embólico) de 30 días en el calendario lunar: luego se deben restar 30 a la epacta. Charles Wheatly proporciona los detalles:
"Así, comenzando el año con marzo (pues esa era la antigua costumbre), permitían treinta días para la luna [que terminaba] en marzo, y veintinueve para esa [que terminaba] en abril; y treinta nuevamente para mayo, y veintinueve para junio, etc., según los antiguos versos:
Impar luna pari, par fiet in impare mense;
In quo completur mensi lunatio detur."Porque el primero, tercero, quinto, séptimo, noveno y undécimo mes, que se llaman imares menses o meses desiguales, tienen sus lunas según un cómputo de treinta días cada una, que por lo tanto se llaman pares lunae o lunas iguales: pero el segundo, cuarto, sexto, octavo, décimo y duodécimo mes, que se llaman pares menses o meses iguales, tienen sus lunas sólo de veintinueve días cada uno, que se llaman impares lunae o lunas desiguales".
— Wheatly 1871, pág. 44
Así, el mes lunar tomó el nombre del mes juliano en el que terminaba. El ciclo metónico de diecinueve años supone que 19 años trópicos son tan largos como 235 meses sinódicos. Así que después de 19 años las lunaciones deberían caer de la misma manera en los años solares, y las epactas deberían repetirse. A lo largo de 19 años la epacta aumenta en 19 × 11 = 209 ≡ 29 ( mod 30) , no 0 (mod 30) . Es decir, 209 dividido por 30 deja un resto de 29 en lugar de ser un múltiplo de 30. Esto es un problema si la compensación solo se hace añadiendo meses de 30 días. [e] Así que después de 19 años, la epacta debe corregirse en un día para que el ciclo se repita. Este es el llamado saltus lunae ("salto de la luna"). El calendario juliano lo soluciona reduciendo la duración del mes lunar que comienza el 1 de julio del último año del ciclo a 29 días, lo que da como resultado tres meses sucesivos de 29 días. [f]
El saltus y los siete meses adicionales de 30 días estaban en gran parte ocultos al estar ubicados en los puntos donde los meses julianos y lunares comienzan aproximadamente al mismo tiempo. Los meses adicionales comenzaron el 1 de enero (año 3), el 2 de septiembre (año 5), el 6 de marzo (año 8), el 3 de enero (año 11), el 31 de diciembre (año 13), el 1 de septiembre (año 16) y el 5 de marzo (año 19). [35] [36] El número de secuencia del año en el ciclo de 19 años se llama " número áureo " y se da por la fórmula
- GN = ( Y mod 19) + 1
Es decir, el número del año Y en la era cristiana se divide por 19, y el resto más 1 es el número áureo. (Algunas fuentes especifican que se debe sumar 1 antes de tomar el resto; en ese caso, se debe tratar un resultado de 0 como el número áureo 19. En la fórmula anterior tomamos primero el resto y luego sumamos 1, por lo que no es necesario tal ajuste.) [g]
Los ciclos de 19 años no tienen todos la misma duración, ya que pueden tener cuatro o cinco años bisiestos. Pero un período de cuatro ciclos, 76 años (un ciclo calípico ), tiene una duración de 76 × 365 + 19 = 27.759 días (si no cruza una división de siglos). Hay 235 × 4 = 940 meses lunares en este período, por lo que la duración media es 27759 / 940 o unos 29,530851 días. Hay 76 × 6 = 456 meses lunares nominales habituales de 30 días y la misma cantidad de meses nominales habituales de 29 días, pero con 19 de estos alargados en un día en los días bisiestos, más 24 meses intercalados de 30 días y cuatro meses intercalados de 29 días. Como esto es más largo que la duración real de un mes sinódico, alrededor de 29,53059 días, la luna llena pascual calculada es cada vez más tardía en comparación con la luna llena astronómica, a menos que se haga una corrección como en el sistema gregoriano (ver más abajo).
El mes pascual o de Pascua es el primero del año en tener su decimocuarto día (su luna llena formal ) el 21 de marzo o después. La Pascua es el domingo después de su decimocuarto día (o, dicho de otra manera, el domingo dentro de su tercera semana). El mes lunar pascual siempre comienza en una fecha en el período de 29 días del 8 de marzo al 5 de abril inclusive. Su decimocuarto día, por lo tanto, siempre cae en una fecha entre el 21 de marzo y el 18 de abril inclusive (en el calendario gregoriano o juliano, para el sistema occidental y oriental, respectivamente), y el domingo siguiente cae necesariamente en una fecha en el rango del 22 de marzo al 25 de abril inclusive. Sin embargo, en el sistema occidental la Pascua no puede caer el 22 de marzo durante el período de 300 años de 1900-2199 (ver más abajo). En el calendario solar, la Pascua se llama fiesta movible ya que su fecha varía dentro de un rango de 35 días. Pero en el calendario lunar, la Pascua es siempre el tercer domingo del mes lunar pascual, y no es más "movible" que cualquier festividad que esté fijada a un día particular de la semana y a una semana dentro de un mes, como el Día de Acción de Gracias .
Métodos tabulares
La reforma gregoriana de lacomputador
Esta sección necesita citas adicionales para su verificación . ( marzo de 2019 ) |
Como la reforma del cómputo fue la motivación principal para la introducción del calendario gregoriano en 1582, se introdujo una metodología de cómputo correspondiente junto con el nuevo calendario. [h] El método general de trabajo fue dado por Clavius en los Seis Cánones (1582), y una explicación completa siguió en su Explicatio (1603). [37]
El Domingo de Pascua es el domingo siguiente a la fecha de la luna llena pascual. La fecha de la luna llena pascual es la fecha de la luna llena eclesiástica del 21 de marzo o después. El método gregoriano deriva las fechas de la luna llena pascual determinando la epacta de cada año. [38] La epacta puede tener un valor de * (0 o 30) a 29 días. Es la edad de la luna en días (es decir, la fecha lunar) el 1 de enero reducida en un día. En su libro The Easter computus and the origins of the Christian era, Alden A Mosshammer afirma incorrectamente [ ¿según quién? ] "Teóricamente, la epacta 30 = 0 representa la luna nueva en su conjunción con el sol. La epacta de 1 representa la primera visibilidad teórica de la primera media luna de la luna. Es a partir de ese punto como día uno que se cuenta el decimocuarto día de la luna". [39]
El decimocuarto día del mes lunar se considera el día de la luna llena . [40] Es el día del mes lunar en el que es más probable que caiga el momento de oposición ("luna llena"). La "luna nueva" es más probable que se haga visible (como una delgada media luna en el cielo occidental después del atardecer) el primer día del mes lunar. La conjunción del sol y la luna ("luna nueva") es más probable que caiga el día anterior, que es el día 29 de un mes "hueco" (de 29 días) y el día 30 de un mes "lleno" (de 30 días).
Históricamente la fecha de luna llena pascual para un año se encontraba a partir de su número de secuencia en el ciclo metónico, llamado número áureo , ciclo que repite la fase lunar el 1 de enero cada 19 años. [41] Este método fue modificado en la reforma gregoriana porque las fechas tabulares se desincronizan con la realidad después de unos dos siglos, pero a partir del método epacto se puede construir una tabla simplificada que tiene una validez de uno a tres siglos. [42] [43]
Los efectos del actual ciclo metónico, que comenzó en 2014, son:
| Año | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | 2024 | 2025 | 2026 | 2027 | 2028 | 2029 | 2030 | 2031 | 2032 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Número dorado | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Epacto [i] | 29 | 10 | 21 | 2 | 13 | 24 | 5 | 16 | 27 | 8 | 19 | * | 11 | 22 | 3 | 14 | 25 | 6 | 17 |
| Fecha de la luna llena pascual [44] | 14 de abril | 3 de abril | 23 de marzo | 11 de abril | 31 de marzo | 18 de abril | 8 de abril | 28 de marzo | 16 de abril | 5 de abril | 25 de marzo | 13 de abril | 2 de abril | 22 de marzo | 10 de abril | 30 de marzo | 17 de abril | 7 de abril | 27 de marzo |
Como se puede ver, la fecha de la luna llena pascual en un año en particular suele ser 11 días antes que en el año anterior, o 19 días después. Las excepciones son que en los años 1, 6 y 17 del ciclo, la fecha es solo 18 días después, y en los años 7 y 18 solo 10 días antes que en el año anterior. En el sistema oriental (ver más abajo), la luna llena pascual suele ser cuatro días después. Es 34 días después en cinco de los 19 años, y 5 días después en los años 6 y 17, porque en esos años, el sistema gregoriano pone la luna llena pascual un día antes de lo que sería normalmente, para mantener la Pascua antes del 26 de abril, como se explica más abajo. En el año 2100 d.C. la diferencia aumentará en un día.
Las epactas se utilizan para encontrar las fechas de la luna nueva de la siguiente manera: escriba una tabla de los 365 días del año (se ignora el día bisiesto). Luego etiquete todas las fechas con un número romano contando hacia abajo, desde "*" (0 o 30), "xxix" (29), hasta "i" (1), comenzando desde el 1 de enero, y repita esto hasta el final del año. Sin embargo, en cada segundo de dicho período cuente solo 29 días y etiquete la fecha con xxv (25) y también con xxiv (24). Trate el período 13 (los últimos once días) como largo, por lo tanto, y asigne las etiquetas "xxv" y "xxiv" a las fechas secuenciales (26 y 27 de diciembre respectivamente). [45]
Añade la etiqueta "25" a las fechas que tienen "xxv" en los períodos de 30 días; pero en los períodos de 29 días (que tienen "xxiv" junto con "xxv") añade la etiqueta "25" a la fecha con "xxvi". La distribución de las longitudes de los meses y la longitud de los ciclos de epactas es tal que cada mes del calendario civil comienza y termina con la misma etiqueta de epacta, excepto febrero y, se podría decir, agosto, que comienza con la doble etiqueta "xxv"/"xxiv" pero termina con la etiqueta simple "xxiv". Esta tabla se llama calendarium . Las lunas nuevas eclesiásticas para cualquier año son aquellas fechas en las que se ingresa la epacta para el año. [45]
Si la epacta del año es, por ejemplo, el 27, entonces hay una luna nueva eclesiástica en cada fecha de ese año que tenga la etiqueta de epacta "xxvii" (27). Si la epacta es el 25, entonces hay una complicación, introducida para que la luna nueva eclesiástica no caiga en la misma fecha dos veces durante un ciclo metónico. Si el ciclo de epactas en vigor incluye la epacta 24 (como lo hace el ciclo en uso desde 1900 y hasta 2199), entonces una epacta de 25 pone la luna nueva eclesiástica el 4 de abril (que tiene la etiqueta "25"), de lo contrario es el 5 de abril (que tiene la etiqueta "xxv"). [45]
Una epacta de 25 que dé el 4 de abril solo puede ocurrir si el número áureo es mayor que 11. En cuyo caso serán 11 años después de un año con epacta 24. Así, por ejemplo, en 1954 el número áureo era 17, la epacta era 25, la luna nueva eclesiástica se calculó el 4 de abril, la luna llena el 17 de abril. La Pascua fue el 18 de abril en lugar del 25 de abril como habría sido de otra manera, como en 1886 cuando el número áureo era 6. Este sistema intercala automáticamente siete meses por ciclo metónico.
Etiqueta todas las fechas de la tabla con las letras "A" a "G", comenzando desde el 1 de enero, y repítelas hasta el final del año. Si, por ejemplo, el primer domingo del año es el 5 de enero, que tiene la letra "E", entonces todas las fechas con la letra "E" son domingos ese año. Entonces "E" se llama la letra dominical para ese año, de dies dominica (del latín "el día del Señor"). La letra dominical retrocede una posición cada año. En los años bisiestos después del 24 de febrero, los domingos caen en la letra anterior del ciclo, por lo que los años bisiestos tienen dos letras dominicales: la primera para antes, la segunda para después del día bisiesto.
En la práctica, para calcular la Pascua, no es necesario hacer esto para los 365 días del año. Para las epactas, marzo es exactamente igual que enero, por lo que no es necesario calcular enero ni febrero. Para evitar la necesidad de calcular las letras dominicales de enero y febrero, se comienza con la D para el 1 de marzo. Se necesitan las epactas solo del 8 de marzo al 5 de abril. Esto da lugar a la siguiente tabla:


| Etiqueta | Marzo | DESCARGAR | Abril | DESCARGAR |
|---|---|---|---|---|
| * | 1 | D | ||
| xxix | 2 | mi | 1 | GRAMO |
| xxviii | 3 | F | 2 | A |
| xxvii | 4 | GRAMO | 3 | B |
| xxvi | 5 | A | 4 | do |
| 25 | 6 | B | ||
| xxv | 5 | D | ||
| xxiv | 7 | do | ||
| xxiii | 8 | D | 6 | mi |
| xxii | 9 | mi | 7 | F |
| xxi | 10 | F | 8 | GRAMO |
| xx | 11 | GRAMO | 9 | A |
| XIX | 12 | A | 10 | B |
| xviii | 13 | B | 11 | do |
| xvii | 14 | do | 12 | D |
| xvi | 15 | D | 13 | mi |
| xv | 16 | mi | 14 | F |
| xiv | 17 | F | 15 | GRAMO |
| xiii | 18 | GRAMO | 16 | A |
| xii | 19 | A | 17 | B |
| x | 20 | B | 18 | do |
| incógnita | 21 | do | 19 | D |
| ix | 22 | D | 20 | mi |
| viii | 23 | mi | 21 | F |
| viii | 24 | F | 22 | GRAMO |
| vi | 25 | GRAMO | 23 | A |
| en | 26 | A | 24 | B |
| IV | 27 | B | 25 | do |
| iii | 28 | do | 26 | D |
| ii | 29 | D | 27 | mi |
| i | 30 | mi | 28 | F |
| * | 31 | F | 29 | GRAMO |
| xxix | 30 | A |
Por ejemplo, si la epacta es 27 (xxvii), una luna nueva eclesiástica cae en cada fecha etiquetada como xxvii . La luna llena eclesiástica cae 13 días después. De la tabla anterior, esto da una luna nueva el 4 de marzo y el 3 de abril, y por lo tanto una luna llena el 17 de marzo y el 16 de abril. Entonces, el Día de Pascua es el primer domingo después de la primera luna llena eclesiástica del 21 de marzo o después. (Esta definición usa "el 21 de marzo o después" para evitar ambigüedad con el significado histórico de la palabra "después". En el lenguaje moderno, esta frase simplemente significa "después del 20 de marzo". La definición de "el 21 de marzo o después" se abrevia con frecuencia de forma incorrecta a "después del 21 de marzo" en artículos publicados y basados en la web, lo que resulta en fechas de Pascua incorrectas). En el ejemplo, esta luna llena pascual es el 16 de abril. Si la letra dominical es E, entonces el día de Pascua es el 20 de abril.
La etiqueta " 25 " (a diferencia de "xxv") se utiliza de la siguiente manera: dentro de un ciclo metónico, los años que están separados por 11 años tienen epactas que difieren en un día. Un mes que comienza en una fecha que tiene las etiquetas xxiv y xxv escritas una al lado de la otra tiene 29 o 30 días. Si las epactas 24 y 25 ocurren dentro de un ciclo metónico, entonces las lunas nueva (y llena) caerían en las mismas fechas para estos dos años. Esto es posible para la luna real [j] pero es poco elegante en un calendario lunar esquemático; las fechas deberían repetirse solo después de 19 años. Para evitar esto, en años que tienen epactas 25 y con un Número Áureo mayor que 11, la luna nueva calculada cae en la fecha con la etiqueta 25 en lugar de xxv . Cuando las etiquetas 25 y xxv están juntas, no hay problema ya que son la misma. Esto no traslada el problema al par "25" y "xxvi", porque la epacta 26 más temprana que podría aparecer sería en el año 23 del ciclo, que dura sólo 19 años: hay un saltus lunae en el medio que hace que las lunas nuevas caigan en fechas separadas.
El calendario gregoriano tiene una corrección del año trópico al eliminar tres días bisiestos en 400 años (siempre en un año centenario). Se trata de una corrección de la duración del año trópico, pero no debería tener ningún efecto sobre la relación metónica entre años y lunaciones. Por lo tanto, la epacta se compensa por esto (parcialmente, ver epacta ) restando uno en estos años centenarios. Esta es la llamada corrección solar o "ecuación solar" ("ecuación" se usa en su sentido medieval de "corrección").
Sin embargo, 19 años julianos sin corregir son un poco más largos que 235 lunaciones. La diferencia se acumula hasta un día en unos 308 años, o 0,00324 días por año. En un ciclo, la epacta disminuye debido a la corrección solar en 19 × 0,0075 = 0,1425 en promedio, por lo que un ciclo equivale a 235−0,1425/30 = 234,99525 meses, mientras que en realidad hay 19 × 365,2425 / 29,5305889 ≈ 234,997261 meses sinódicos. La diferencia de 0,002011 meses sinódicos por ciclo de 19 años, o 0,003126 días por año, requiere una corrección lunar ocasional de la epacta. En el calendario gregoriano, esto se hace añadiendo 1 ocho veces en 2.500 años (gregorianos) (algo más de 2500 × 0,003126, o aproximadamente 7,8), siempre en un año de siglo: esta es la llamada corrección lunar (históricamente llamada "ecuación lunar"). La primera se aplicó en 1800, la siguiente es en 2100, y se aplicará cada 300 años excepto por un intervalo de 400 años entre 3900 y 4300, que inicia un nuevo ciclo. En el momento de la reforma, las epactas se cambiaron en 7, aunque se saltaron 10 días, para hacer una corrección de tres días en el momento de las lunas nuevas. [45]
Las correcciones solar y lunar funcionan en direcciones opuestas y en algunos años centenarios (por ejemplo, 1800 y 2100) se anulan entre sí. El resultado es que el calendario lunar gregoriano utiliza una tabla de epactos válida para un período de entre 100 y 300 años. La tabla de epactos que se muestra arriba es válida para el período de 1900 a 2199.
Como se explica a continuación, las fechas de Pascua se repiten después de 5.700.000 años, y durante este período la duración media de un mes eclesiástico es de 2.081.882.250/70.499.183 ≈ 29,5305869 días, [46] que difiere de la duración media real actual de la lunación (29.5305889 d: véase Mes lunar#Mes sinódico ) en la sexta cifra después del punto decimal. Esto corresponde a un error de menos de un día en la fase de la luna a lo largo de 40.000 años, pero de hecho la duración de un día está cambiando (al igual que la duración de un mes sinódico), por lo que el sistema no es preciso en dichos períodos. Véase el artículo ΔT (cronometraje) para obtener información sobre el cambio acumulativo de la duración del día.
Detalles
This section needs additional citations for verification. (July 2020) |
Este método de cálculo tiene varias sutilezas:
Cada mes lunar tiene solo 29 días, por lo que un día debe tener dos (de las 30) etiquetas de epacta asignadas. La razón para mover la etiqueta de epacta "xxv/25" en lugar de cualquier otra parece ser la siguiente: según Dionisio (en su carta introductoria a Petronio), el concilio de Nicea, con la autoridad de Eusebio , estableció que el primer mes del año lunar eclesiástico (el mes pascual) debería comenzar entre el 8 de marzo y el 5 de abril inclusive, y el día 14 caer entre el 21 de marzo y el 18 de abril inclusive, abarcando así un período de (solo) 29 días. Una luna nueva el 7 de marzo, que tiene la etiqueta de epacta "xxiv", tiene su día 14 (luna llena) el 20 de marzo, que es demasiado temprano (no después del 20 de marzo). Así, en los años con epacta "xxiv", si el mes lunar que comienza el 7 de marzo tiene 30 días, la luna nueva pascual se celebra el 6 de abril, lo que es demasiado tarde: la luna llena caería el 19 de abril y la Pascua podría llegar hasta el 26 de abril. En el calendario juliano, la fecha más tardía de la Pascua era el 25 de abril, y la reforma gregoriana mantuvo ese límite. Por lo tanto, la luna llena pascual debe caer a más tardar el 18 de abril y la luna nueva el 5 de abril, que tiene la etiqueta de epacta "xxv". Por lo tanto, el 5 de abril debe tener sus etiquetas de epacta dobles "xxiv" y "xxv". Entonces, la epacta "xxv" debe tratarse de manera diferente, como se explica en el párrafo anterior.
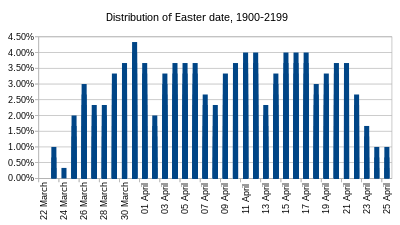
La distribución de frecuencias de la fecha de Pascua no está bien definida, porque cada 100 a 300 años cambia la correspondencia entre el número áureo y el epacto, y la distribución de frecuencias a largo plazo solo es válida durante un período de millones de años (véase más abajo), mientras que el sistema no se utilizará durante tanto tiempo. La correspondencia actual, válida desde 1900 hasta 2199, da fechas de Pascua con frecuencias muy variables. El 22 de marzo nunca puede ocurrir, mientras que el 31 de marzo ocurre 13 veces en este lapso de 300 años.
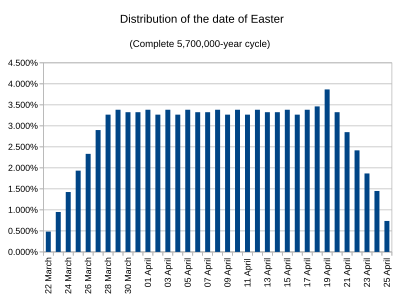
Si nos preguntamos cuál sería la distribución a largo plazo, es decir, a lo largo de todo el período de 5,7 millones de años tras el cual se repiten las fechas, esta distribución se puede encontrar con bastante facilidad y es bastante diferente de la distribución en el período de 1900 a 2199, o incluso de la distribución en el período desde la reforma hasta ahora. La fecha de Pascua en un año determinado depende únicamente de la epacta del año, su número áureo y su letra dominical , que nos dice qué días son domingos (más precisamente, la letra dominical para la parte del año después de febrero, que es diferente en los años bisiestos de la letra de enero y febrero). (El número áureo sólo importa cuando la epacta es 25, como se explicó anteriormente.) Si avanzamos 3.230.000 años a partir de un año en particular, encontramos un año en el mismo punto en el ciclo gregoriano de 400 años y con el mismo número áureo, pero con la epacta aumentada en 1. Por lo tanto, a largo plazo, las treinta epactas son igualmente probables. Por otro lado, las letras dominicales no tienen todas la misma frecuencia: los años con las letras A y C (al final del año) ocurren el 14% del tiempo cada uno, E y F ocurren el 14,25% del tiempo, y B, D y G ocurren el 14,5% del tiempo. Teniendo en cuenta la complicación relacionada con la epacta 25, esto da la distribución que se muestra en el segundo gráfico. El 19 de abril es el más común porque cuando la epacta es 25 la luna llena eclesiástica cae el 17 o 18 de abril (dependiendo del número áureo), y también cae en estas fechas cuando la epacta es 26 o 24, respectivamente. Hay siete días en los que la luna llena puede caer, incluyendo el 17 y el 18 de abril, para que la Pascua sea el 19 de abril (esta es también la fecha más tardía posible de Pascua en la que la luna llena eclesiástica puede caer en sábado, ya que el 18 de abril es la fecha más tardía para la luna llena eclesiástica, que Pascua es el día siguiente si la luna llena eclesiástica es un sábado). [45] Como consecuencia, el 19 de abril es la fecha en la que la Pascua cae con más frecuencia en el calendario gregoriano, en aproximadamente el 3,87% de los años. El 22 de marzo es el menos frecuente, con un 0,48%. [47] [45]
La relación entre las fechas del calendario lunar y solar se hace independiente del esquema de días bisiestos para el año solar. Básicamente, el calendario gregoriano todavía utiliza el calendario juliano con un día bisiesto cada cuatro años, por lo que un ciclo metónico de 19 años tiene 6.940 o 6.939 días con cinco o cuatro días bisiestos. Ahora el ciclo lunar cuenta solo 19 × 354 + 19 × 11 = 6.935 días . Al no etiquetar y contar el día bisiesto con un número de epacta, sino que la siguiente luna nueva cae en la misma fecha del calendario que sin el día bisiesto, la lunación actual se extiende por un día, [k] y las 235 lunaciones cubren tantos días como los 19 años (siempre que los 19 años no incluyan una "corrección solar" como en 1900). De modo que la carga de sincronizar el calendario con la luna (precisión a medio plazo) recae en el calendario solar, que puede utilizar cualquier esquema de intercalación adecuado, todo ello bajo el supuesto de que 19 años solares = 235 lunaciones (lo que crea una inexactitud a largo plazo si no se corrige con una "corrección lunar"). Una consecuencia es que la edad estimada de la luna puede tener un día de diferencia, y también que las lunaciones que contienen el día bisiesto pueden tener una duración de 31 días, lo que nunca sucedería si se siguiera la luna real (inexactitudes a corto plazo). Este es el precio de un ajuste regular al calendario solar.
Desde la perspectiva de aquellos que quisieran utilizar el ciclo pascual gregoriano como calendario para todo el año, existen algunos fallos en el calendario lunar gregoriano [48] (aunque no tienen efecto sobre el mes pascual y la fecha de Pascua):
- Se producen lunaciones de 31 (y a veces 28) días.
- Si un año con el Número Áureo 19 tiene epacta 19, entonces la última luna nueva eclesiástica cae el 2 de diciembre; la siguiente debería ocurrir el 1 de enero. Sin embargo, al comienzo del nuevo año, un saltus lunae aumenta la epacta en otra unidad, y la luna nueva debería haber ocurrido el día anterior. Por lo tanto, se pierde una luna nueva. El calendarium del Missale Romanum toma esto en cuenta asignando la etiqueta de epacta "19" en lugar de "xx" al 31 de diciembre de dicho año, convirtiendo esa fecha en la luna nueva. Ocurría cada 19 años cuando la tabla de epactas gregoriana original estaba en vigor (por última vez en 1690), y la próxima vez ocurre en 8511.
- Si la epacta de un año es 20, una luna nueva eclesiástica cae el 31 de diciembre. Si ese año cae antes de un año centenario, entonces, en la mayoría de los casos, una corrección solar reduce la epacta del año nuevo en uno: la epacta resultante "*" significa que otra luna nueva eclesiástica se cuenta el 1 de enero. Por lo tanto, formalmente, ha transcurrido una lunación de un día. Esto sucederá nuevamente en 4199-4200.
- Otros casos límite ocurren (mucho) más tarde, y si se siguen estrictamente las reglas y no se tratan especialmente, generan fechas de luna nueva sucesivas que están separadas por 1, 28, 59 o (muy raramente) 58 días.
Un análisis cuidadoso muestra que a través de la forma en que se utilizan y corrigen en el calendario gregoriano, las epactas son en realidad 1/30 de una lunación y no de días completos. Ver epacto para una discusión.
Las correcciones solares y lunares se repiten después de 4 × 25 = 100 siglos. En ese período, la epacta para un número áureo dado cambia en un total de −1 × 3/4× 100 + 1 × 8/25 × 100 = −43 ≡ 17 mod 30 . Este es primo de las 30 epactas posibles, por lo que se necesitan 100 × 30 = 3000 siglos antes de que las aplicaciones de las epactas se repitan; y 3000 × 19 = 57 000 siglos antes de que se repitan en el mismo número áureo. No es obvio cuántas Lunas Nuevas eclesiásticas se cuentan en este período de 5,7 millones de años. Los ciclos metónicos suman (5 700 000/19) × 235 = 70 500 000 lunaciones. Pero hay correcciones netas de −43 × (5.700.000/10.000) a las epactas, que divididas por 30 suman una corrección de −817 lunaciones, para un total de 70.499.183 lunaciones. Este número parece haber sido derivado por primera vez por Magnus Georg Paucker en 1837. [49] También se menciona en el capítulo sobre calendarios (p. 744) en el Almanaque Náutico de 1931 [50] y en el Suplemento Explicativo de 1992 (p. 582). [51] [l] Así que las fechas de Pascua gregoriana se repiten exactamente en el mismo orden solo después de 5.700.000 años, 70.499.183 lunaciones o 2.081.882.250 días; La duración media de la lunación es entonces de 2.081.882.250/70.499.183 = 29,53058690 días. Por supuesto, el calendario tendría que ajustarse después de algunos milenios debido a los cambios en la duración del año trópico, el mes sinódico y el día.

Esto plantea la pregunta de por qué el calendario lunar gregoriano tiene correcciones solares y lunares separadas, que a veces se anulan entre sí. El trabajo original de Lilius no se ha conservado, pero su propuesta fue descrita en el Compendium Novae Rationis Restituendi Kalendarium , que circuló en 1577, en el que se explica que el sistema de corrección que ideó iba a ser una herramienta perfectamente flexible en manos de los futuros reformadores del calendario, ya que el calendario solar y lunar podrían corregirse a partir de entonces sin interferencia mutua. [52] Un ejemplo de esta flexibilidad lo proporcionó una secuencia de intercalación alternativa derivada de las teorías de Copérnico, junto con sus correspondientes correcciones de epacto. [53]
Las "correcciones solares" anulan aproximadamente el efecto de las modificaciones gregorianas a los días bisiestos del calendario solar en el calendario lunar: devuelven (parcialmente) el ciclo de epactas a la relación metónica original entre el año juliano y el mes lunar. El desajuste inherente entre el sol y la luna en este ciclo básico de 19 años se corrige luego cada tres o cuatro siglos mediante la "corrección lunar" de las epactas. Sin embargo, las correcciones de epactas ocurren al comienzo de los siglos gregorianos, no de los julianos, y por lo tanto el ciclo metónico juliano original no se restaura por completo.
Si bien las sustracciones netas de 4 × 8 − 3 × 25 = 43 epactas podrían distribuirse uniformemente a lo largo de 10 000 años (como propuso, por ejemplo, Lichtenberg 2003, pp. 45-76), si se combinan las correcciones, las imprecisiones de los dos ciclos también se suman y no se pueden corregir por separado.
Las proporciones de días (solares medios) por año y días por lunación cambian debido a variaciones intrínsecas a largo plazo en las órbitas y porque la rotación de la Tierra se está desacelerando debido a la desaceleración de las mareas , por lo que los parámetros gregorianos se vuelven cada vez más obsoletos.
Esto afecta la fecha del equinoccio, pero sucede que el intervalo entre los equinoccios del norte (primavera del hemisferio norte) ha sido bastante estable a lo largo de los tiempos históricos, especialmente si se mide en tiempo solar medio. [54] [55]
También la deriva de las lunas llenas eclesiásticas calculadas por el método gregoriano en comparación con las lunas llenas verdaderas se ve menos afectada de lo que se esperaría, porque el aumento de la duración del día se compensa casi exactamente con el aumento de la duración del mes, ya que el frenado de las mareas transfiere el momento angular de la rotación de la Tierra al momento angular orbital de la Luna.
El valor ptolemaico de la duración del mes sinódico medio, establecido alrededor del siglo IV a. C. por los babilonios, es de 29 días, 12 h y 44 min .+1/3 s (véase Kidinnu ); el valor actual es 0,46 s menos (véase Luna nueva ). En el mismo período histórico, la duración del año tropical medio ha disminuido unos 10 s (todos los valores corresponden al tiempo solar).
Ley del Calendario Británico yLibro de oración común
La parte de la sección de métodos tabulares anterior describe los argumentos y métodos históricos mediante los cuales la Iglesia Católica decidió las fechas actuales del Domingo de Pascua a fines del siglo XVI. En Gran Bretaña, donde todavía se usaba el calendario juliano, el Domingo de Pascua se definió, desde 1662 hasta 1752 (de acuerdo con la práctica anterior), mediante una simple tabla de fechas en el Libro de Oración Común Anglicano (decretado por la Ley de Uniformidad de 1662 ). La tabla estaba indexada directamente por el número áureo y la letra del domingo , que (en la sección de Pascua del libro) se suponía que ya se conocían.
Para el Imperio Británico y sus colonias, la nueva determinación de la fecha del Domingo de Pascua fue definida por lo que ahora se llama la Ley de Calendario (Nuevo Estilo) de 1750 con su anexo. El método fue elegido para dar fechas que coincidieran con la regla gregoriana que ya se usaba en otros lugares. La ley requería que se pusiera en el Libro de Oración Común y, por lo tanto, es la regla anglicana general. La ley original se puede ver en los Estatutos Británicos en General de 1765. [ 56] El anexo de la ley incluye la definición: " El día de Pascua (del que dependen el resto) es siempre el primer domingo después de la Luna llena , que ocurre en, o después del vigésimo primer día de marzo . Y si la Luna llena ocurre en domingo , el día de Pascua es el domingo siguiente". El anexo posteriormente utiliza los términos "Luna llena Pascual" y "Luna llena Eclesiástica", dejando en claro que se aproximan a la luna llena real.
El método es muy distinto del descrito anteriormente en § La reforma gregoriana del cómputo. Para un año general, primero se determina el número áureo , luego se utilizan tres tablas para determinar la letra dominical , una "cifra" y la fecha de la luna llena pascual, de la que se deduce la fecha del Domingo de Pascua. La epacta no aparece explícitamente. Se pueden utilizar tablas más sencillas para períodos limitados (como 1900-2199) durante los cuales la cifra (que representa el efecto de las correcciones solar y lunar) no cambia. Los detalles de Clavius se emplearon en la construcción del método, pero no juegan ningún papel posterior en su uso. [57] [58]
JR Stockton muestra su derivación de un algoritmo informático eficiente rastreable hasta las tablas del libro de oraciones y la Ley del Calendario (asumiendo que hay una descripción de cómo usar las Tablas a mano), y verifica sus procesos calculando tablas coincidentes. [59]
calendario juliano

El método para calcular la fecha de la luna llena eclesiástica que era estándar para la Iglesia occidental antes de la reforma del calendario gregoriano, y que todavía usan hoy la mayoría de los cristianos orientales , hacía uso de una repetición no corregida del ciclo metónico de 19 años en combinación con el calendario juliano. En términos del método de las epactas discutido anteriormente, utilizó efectivamente una sola tabla de epactas que comenzaba con una epacta de 0, que nunca se corrigió. En este caso, la epacta se contabilizó el 22 de marzo, la fecha más temprana aceptable para la Pascua. Esto se repite cada 19 años, por lo que solo hay 19 fechas posibles para la luna llena pascual desde el 21 de marzo hasta el 18 de abril inclusive.
Como no hay correcciones como las que hay en el calendario gregoriano, la luna llena eclesiástica se desvía de la luna llena verdadera en más de tres días cada milenio. Ya es unos días más tarde. Como resultado, las iglesias orientales celebran la Pascua una semana más tarde que las iglesias occidentales alrededor del 44% del tiempo, y el mismo día alrededor del 30% del tiempo. (La Pascua oriental se celebra ocasionalmente cuatro o cinco semanas más tarde porque el calendario juliano está 13 días detrás del gregoriano en 1900-2099, y por lo tanto la luna llena pascual gregoriana a veces es antes del 21 de marzo juliano).
El número de secuencia de un año en el ciclo de 19 años se denomina número áureo . Este término se utilizó por primera vez en el poema computista Massa Compoti de Alexander de Villa Dei en 1200. Un escriba posterior agregó el número áureo a las tablas compuestas originalmente por Abbo de Fleury en 988.
La afirmación de la Iglesia Católica en la bula papal de 1582 Inter gravissimas , que promulgó el calendario gregoriano, de que restableció "la celebración de la Pascua según las reglas fijadas por... el gran concilio ecuménico de Nicea" [60] se basó en una afirmación falsa de Dionisio el Exiguo (525) de que "determinamos la fecha del día de Pascua... de acuerdo con la propuesta acordada por los 318 Padres de la Iglesia en el Concilio de Nicea". [61]
Sin embargo, el Primer Concilio de Nicea (325) no proporcionó ninguna regla explícita para determinar esa fecha, sino que solo escribió "todos nuestros hermanos en Oriente que antiguamente seguían la costumbre de los judíos deben celebrar de ahora en adelante la mencionada fiesta sagrada de Pascua al mismo tiempo con los romanos y ustedes mismos [la Iglesia de Alejandría] y todos aquellos que han observado la Pascua desde el principio". [62] El computus medieval se basó en el computus alejandrino , que fue desarrollado por la Iglesia de Alejandría durante la primera década del siglo IV utilizando el calendario alejandrino . [63]
El Imperio romano oriental lo aceptó poco después de 380 después de convertir el computus al calendario juliano. [64] Roma lo aceptó en algún momento entre los siglos VI y IX. Las Islas Británicas lo aceptaron durante el siglo VIII, excepto algunos monasterios. [ cita requerida ] Francia (toda Europa occidental excepto Escandinavia (pagana), las Islas Británicas, la península Ibérica y el sur de Italia) lo aceptó durante el último cuarto del siglo VIII. [ cita requerida ]
El último monasterio celta en aceptarlo, Iona , lo hizo en 716. [ cita requerida ] El último monasterio inglés en aceptarlo lo hizo en 931. [ cita requerida ] Antes de estas fechas, otros métodos producían fechas del Domingo de Pascua que podían diferir hasta en cinco semanas. [ cita requerida ]
Esta es la tabla de fechas de luna llena pascual para todos los años julianos desde 931:
Número dorado | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Fecha de luna llena pascual (juliana) | 5 de abril | 25 de marzo | 13 de abril | 2 de abril | 22 de marzo | 10 de abril | 30 de marzo | 18 de abril | 7 de abril | 27 de marzo | 15 de abril | 4 de abril | 24 de marzo | 12 de abril | 1 de abril | 21 de marzo | 9 de abril | 29 de marzo | 17 de abril |
Fecha de la luna llena pascual , 1900-2099, calendario gregoriano | 18 de abril | 7 de abril | 26 de abril | 15 de abril | 4 de abril | 23 de abril | 12 de abril | 1 de mayo | 20 de abril | 9 de abril | 28 de abril | 17 de abril | 6 de abril | 25 de abril | 14 de abril | 3 de abril | 22 de abril | 11 de abril | 30 de abril |
Fecha de la luna llena pascual , occidental, 1900-2199 (gregoriana) | 14 de abril | 3 de abril | 23 de marzo | 11 de abril | 31 de marzo | 18 de abril | 8 de abril | 28 de marzo | 16 de abril | 5 de abril | 25 de marzo | 13 de abril | 2 de abril | 22 de marzo | 10 de abril | 30 de marzo | 17 de abril | 7 de abril | 27 de marzo |
Como se mencionó anteriormente, estas lunas llenas pascuales son 4, 5 o 34 días más tarde que en el sistema occidental, y son alrededor de tres días más tarde que la luna llena astronómica. (Por ejemplo, el eclipse lunar de abril de 2015 fue el 4 de abril en el calendario gregoriano, o el 22 de marzo en el calendario juliano, pero la luna llena pascual para ese año (número áureo 2) fue el 25 de marzo en el calendario juliano). Siempre que hay una corrección lunar, las diferencias entre las lunas llenas eclesiásticas occidentales y orientales aumentan en 1, por lo que desde 2100 a 2399 las diferencias serán de 5, 6 o 35 días. El rango de fechas en el calendario gregoriano de la luna llena pascual oriental se mueve un día más tarde cada vez que hay una corrección solar, por lo que desde 2100 a 2199 será del 5 de abril al 9 de mayo. En la actualidad, hay cinco años por ciclo en los que la Pascua oriental se produce varias semanas después que la occidental, en los números áureos 3, 8, 11, 14 y 19. Esto aumentará a seis veces por ciclo en 2200 (añadiendo el número áureo 6), a siete en 2300 (añadiendo el número áureo 17), luego volverá a seis en 2400 (corrección lunar y sin corrección solar), volverá a siete en 2500 y llegará a ocho solo en 2900 (añadiendo el número áureo 9). [ cita requerida ]
Ejemplo de cálculo utilizando esta tabla:
El número áureo para 1573 es 16 ( 1573 + 1 = 1574 ; 1574 ÷ 19 = 82 resto 16 ). Según la tabla, la luna llena pascual para el número áureo 16 es el 21 de marzo. Según la tabla de la semana, el 21 de marzo es sábado. El Domingo de Pascua es el domingo siguiente, 22 de marzo.
Así, para una fecha dada de luna llena eclesiástica, hay siete posibles fechas de Pascua. El ciclo de las letras dominicales, no se repite en siete años: debido a las interrupciones del día bisiesto cada cuatro años, el ciclo completo en el que los días de la semana se repiten en el calendario de la misma manera, es de 4 × 7 = 28 años, el ciclo solar . Por lo tanto, las fechas de Pascua se repiten en el mismo orden después de 4 × 7 × 19 = 532 años. Este ciclo pascual también se llama ciclo victoriano , en honor a Victorio de Aquitania, quien lo introdujo en Roma en 457.
Se sabe que fue utilizado por primera vez por Aniano de Alejandría a principios del siglo V. También se lo ha llamado a veces erróneamente ciclo dionisíaco , en honor a Dionisio el Exiguo , quien preparó tablas de Pascua que comenzaron en 532. Al parecer, no se dio cuenta de que el cómputo alejandrino que describió tenía un ciclo de 532 años, aunque sí se dio cuenta de que su tabla de 95 años no era un ciclo verdadero. Beda el Venerable (siglo VII) parece haber sido el primero en identificar el ciclo solar y explicar el ciclo pascual a partir del ciclo metónico y el ciclo solar.
En la Europa occidental medieval, las fechas de la luna llena pascual (14 de Nisán) mencionadas anteriormente se podían memorizar con la ayuda de un poema aliterativo de 19 líneas en latín: [65] [66]
Nonae Aprilis norunt quinos V octonas calendas Así que depromunt. I Idus de abril Por eso el sexo, VI nonae cuaternae nombre dipondio. II Artículo no definido ambiente quinos, V Cuarteto IDU capitán ternos. III Calendario de Ternas seni titulante, VI Cuarteto dene cubano en quadris. III Septenas idus septiembre eligunt, VII calendario de senae salida por terceros, III Denis Septentris donante así. I Pridie nonas porro cuaternis, III nona calendae nota altísima septenis. VII Idus de Pridie panditur quinis, V calendario de abril exprimunt unus. I Nombre del duodeno doctrina cuaternaria, III Muestra quintam esperma duobus. II Calendae cuaternae quinque coniciunt, V constante de quindeno tribus adeptis. III
La primera media línea de cada línea indica la fecha de la luna llena pascual de la tabla anterior para cada año del ciclo de 19 años. La segunda media línea indica el día ferial regular o el desplazamiento del día de la semana del día de la luna llena pascual de ese año con respecto al día concurrente o el día de la semana del 24 de marzo. [67] El día ferial regular se repite en números romanos en la tercera columna.
Fechas de Pascua “paradójicas”
Debido a las discrepancias entre las aproximaciones de los cálculos computacionales de la hora del equinoccio de primavera medio (hemisferio norte) y de las fases lunares, y los valores verdaderos calculados según los principios astronómicos, a veces surgen diferencias entre la fecha de Pascua según el cálculo computacional y la fecha hipotética de Pascua calculada mediante métodos astronómicos utilizando los principios atribuidos a los Padres de la Iglesia. Estas discrepancias se denominan fechas de Pascua "paradójicas". [68]
En su Kalendarium de 1474, Regiomontanus calculó el tiempo exacto de todas las conjunciones del Sol y la Luna para la longitud de Núremberg según las Tablas Alfonsinas para el período de 1475 a 1531. En su trabajo tabuló 30 casos en los que la Pascua del cómputo juliano discrepaba con la Pascua calculada utilizando la Luna Nueva astronómica . En dieciocho casos la fecha difería en una semana, en siete casos en 35 días y en cinco casos en 28 días. [68]
Ludwig Lange investigó y clasificó diferentes tipos de fechas paradójicas de Pascua utilizando el cómputo gregoriano . [69] En los casos en los que la primera luna llena vernal según el cálculo astronómico ocurre un domingo y el cómputo da el mismo domingo que la Pascua, la Pascua celebrada ocurre una semana antes en comparación con la Pascua "astronómicamente" correcta hipotética. Lange llamó a este caso una paradoja semanal negativa (hebdomadal) (paradoja H−). Si el cálculo astronómico da un sábado para la primera luna llena vernal y la Pascua no se celebra el domingo inmediatamente posterior sino una semana después, la Pascua se celebra según el cómputo una semana demasiado tarde en comparación con el resultado astronómico. Clasificó tales casos como una paradoja semanal positiva (hebdomadal) (paradoja H+). [69]
Las discrepancias son aún mayores si hay una diferencia según el equinoccio de primavera con respecto a la teoría astronómica y la aproximación del computus . Si la luna llena equinoccial astronómica cae antes de la luna llena equinoccial computacional, la Pascua se celebrará cuatro o incluso cinco semanas demasiado tarde. Tales casos se denominan paradoja equinoccial positiva (paradoja A+) según Lange. En el caso inverso, cuando la luna llena equinoccial computacional cae un mes antes de la luna llena equinoccial astronómica, la Pascua se celebra cuatro o cinco semanas demasiado temprano. Tales casos se denominan paradoja equinoccial negativa (paradoja A−). [69]
Las paradojas equinocciales son siempre válidas globalmente para toda la Tierra, porque la secuencia de equinoccios y luna llena no depende de la longitud geográfica. En cambio, las paradojas semanales son locales en la mayoría de los casos y son válidas sólo para una parte de la Tierra, porque el cambio de día entre sábado y domingo depende de la longitud geográfica. Los cálculos computacionales se basan en tablas astronómicas válidas para la longitud de Venecia, que Lange llamó longitud gregoriana. [69]
En los siglos XXI y XXII [69] [70] las fechas paradójicas semanales negativas de Pascua ocurren en 2049, 2076, 2106, 2119 (global), 2133, 2147, 2150, 2170 y 2174. Las fechas paradójicas semanales positivas ocurren en 2045, 2069, 2089 (global) y 2096. Las fechas paradójicas equinocciales positivas ocurren en 2019, 2038, 2057, 2076, 2095, 2114, 2133, 2152, 2171 y 2190. [70]
En 2076 y 2133 se producen paradojas dobles (equinoccial positiva y semanal negativa). Las paradojas equinocciales negativas son extremadamente raras. Se producen sólo dos veces hasta el año 4000 en 2353, cuando la Pascua se adelanta cinco semanas y en 2372, cuando la Pascua se adelanta cuatro semanas. [70]
Algoritmos
Nota sobre operaciones
Al expresar algoritmos de Pascua sin utilizar tablas, se ha acostumbrado a emplear solo las operaciones enteras suma , resta , multiplicación , división , módulo y asignación , ya que es compatible con el uso de calculadoras mecánicas o electrónicas simples. Esa restricción no es deseable para la programación informática, donde están disponibles los operadores y declaraciones condicionales, así como las tablas de consulta. Se puede ver fácilmente cómo se puede realizar la conversión de día de marzo (22 a 56) a día y mes (22 de marzo a 25 de abril) como if (DoM > 31) {Day=DoM-31, Month=Apr} else {Day=DoM, Month=Mar}. Más importante aún, el uso de tales condicionales también simplifica el núcleo del cálculo gregoriano.
Algoritmo de Pascua de Gauss
En 1800, el matemático Carl Friedrich Gauss presentó este algoritmo para calcular la fecha de la Pascua juliana o gregoriana. [71] [72] Corrigió la expresión para calcular la variable p en 1816. [73] En 1800, afirmó incorrectamente que p = floor (a/3 ) = ⌊ a/3 ⌋ . En 1807, reemplazó la condición (11 M + 11) mod 30 < 19 con la más simple a > 10 . En 1811, limitó su algoritmo solo a los siglos XVIII y XIX, y afirmó que el 26 de abril siempre se reemplaza por el 19 y el 25 de abril por el 18 de abril en las circunstancias indicadas. En 1816, agradeció a su estudiante Peter Paul Tittel por señalar que p estaba mal en la versión original. [74]
| Variable | Expresión | año = 1777 | 2024 | 2025 |
|---|---|---|---|---|
| a = | año mod 19 | 10 | 10 | 11 |
| b = | año mod 4 | 1 | 0 | 1 |
| c = | año mod 7 | 6 | 1 | 2 |
| k = | año div 100 = ⌊ año/100 ⌋ | 17 | 20 | 20 |
| p = | (13 + 8k ) div25 = ⌊ 13 + 8k/25 ⌋ | 5 | 6 | 6 |
| q = | kdiv 4 = ⌊ a/4 ⌋ | 4 | 5 | 5 |
| M = | (15 − p + k − q ) módulo 30 | 23 | 24 | 24 |
| N = | (4 + k − q ) módulo 7 | 3 | 5 | 5 |
| Para la Pascua juliana en el calendario juliano M = 15 y N = 6 ( k , p y q son innecesarios) | ||||
| d = | (19 a + M ) módulo 30 | 3 | 4 | 23 |
| mi = | ( 2b + 4c +6d + N ) módulo 7 | 5 | 5 | 6 |
| Día de Pascua de marzo = | 22 + d + e | 30 | 31 | 51 |
| Día de Pascua de abril = | d + e − 9 | -1 | 0 | 20 |
| (11 M + 11) módulo 30 | 24 | 5 | 5 | |
| Si d = 28, e = 6 y (11 M + 11) mod 30 < 19, reemplace el 25 de abril por el 18 de abril. | ||||
| Si d = 29 y e = 6, reemplace el 26 de abril por el 19 de abril. | ||||
El análisis del algoritmo de Pascua de Gauss se divide en dos partes. La primera parte es el seguimiento aproximado de la órbita lunar y la segunda parte es el desfase determinista exacto para obtener un domingo posterior a la luna llena.
La primera parte consiste en determinar la variable d , el número de días (contando desde el 22 de marzo) hasta el día siguiente a la luna llena. La fórmula para d contiene los términos 19 a y la constante M . a es la posición del año en el ciclo de fases lunares de 19 años, en el que, por hipótesis, el movimiento de la Luna en relación con la Tierra se repite cada 19 años calendario. En tiempos más antiguos, 19 años calendario se equiparaban a 235 meses lunares (el ciclo metónico), lo que es notablemente cercano ya que 235 meses lunares son aproximadamente 6939,6813 días y 19 años son en promedio 6939,6075 días.
La expresión (19 a + M ) mod 30 se repite cada 19 años dentro de cada siglo, ya que M se determina por siglo. El ciclo de 19 años no tiene nada que ver con el '19' en 19 a ; es solo una coincidencia que aparezca otro '19'. El '19' en 19 a surge de corregir el desajuste entre un año calendario y un número entero de meses lunares.
Un año calendario (no bisiesto) tiene 365 días y lo más cercano que se puede llegar a un número entero de meses lunares es 12 × 29,5 = 354 días. La diferencia es de 11 días, que se debe corregir retrasando 11 días la aparición de luna llena del año siguiente. Pero en aritmética módulo 30, restar 11 es lo mismo que sumar 19, de ahí la suma de 19 por cada año añadido, es decir, 19 a .
La M en 19 a + M sirve para tener un punto de partida correcto al inicio de cada siglo. Se determina mediante un cálculo que toma el número de años bisiestos hasta ese siglo donde k inhibe un día bisiesto cada 100 años y q lo reinstala cada 400 años, lo que da ( k − q ) como el número total de inhibiciones al patrón de un día bisiesto cada cuatro años. Por lo tanto, agregamos ( k − q ) para corregir los días bisiestos que nunca ocurrieron. p corrige el hecho de que la órbita lunar no sea completamente descriptible en términos enteros.
El rango de días considerados para la luna llena para determinar la Pascua son el 21 de marzo (el día del equinoccio eclesiástico de primavera) al 18 de abril, un rango de 29 días. Sin embargo, en la aritmética módulo 30 de la variable d y la constante M , las cuales pueden tener valores enteros en el rango de 0 a 29, el rango es 30. Por lo tanto, se realizan ajustes en casos críticos. Una vez que se determina d , este es el número de días que se deben agregar al 22 de marzo (el día después de la luna llena más temprana posible permitida, que coincide con el equinoccio eclesiástico de primavera) para obtener la fecha del día después de la luna llena.
Así, la primera fecha permitida para la Pascua es el 22 de marzo + d + 0 , ya que la Pascua se celebra el domingo siguiente a la luna llena eclesiástica; es decir, si la luna llena cae el domingo 21 de marzo, la Pascua se celebra 7 días después, mientras que si la luna llena cae el sábado 21 de marzo, la Pascua es el 22 de marzo siguiente.
La segunda parte es encontrar e , los días de diferencia adicionales que deben agregarse a la diferencia de fecha d para que llegue a un domingo. Dado que la semana tiene 7 días, la diferencia debe estar en el rango de 0 a 6 y determinarse mediante aritmética de módulo 7. e se determina calculando 2 b + 4 c + 6 d + N mod 7 . Estas constantes pueden parecer extrañas al principio, pero son bastante fáciles de explicar si recordamos que operamos bajo aritmética de módulo 7. Para empezar, 2 b + 4 c garantiza que nos ocupamos del hecho de que los días de la semana se deslizan para cada año.
Un año normal tiene 365 días, pero 52 × 7 = 364 , por lo que 52 semanas completas suponen un día menos. Por lo tanto, cada año consecutivo, el día de la semana "se desplaza un día hacia adelante", es decir, si el 6 de mayo fue miércoles un año, será jueves el año siguiente (sin tener en cuenta los años bisiestos). Tanto b como c aumentan en uno para un avance de un año (sin tener en cuenta los efectos del módulo). La expresión 2 b + 4 c aumenta en 6, pero recuerda que esto es lo mismo que restar 1 mod 7.
Restar 1 es exactamente lo que se requiere para un año normal: dado que el día de la semana se adelanta un día, debemos compensar un día menos para llegar al día de la semana correcto (es decir, domingo). Para un año bisiesto, b se convierte en 0 y, por lo tanto, 2 b es 0 en lugar de 8, lo que, según módulo 7, es otra resta por 1, es decir, una resta total por 2, ya que los días de la semana posteriores al día bisiesto de ese año se adelantan dos días.
La expresión 6 d funciona de la misma manera. Aumentar d por un número y indica que la luna llena ocurre y días después este año, y por lo tanto deberíamos compensar y días menos. Sumar 6 d es mod 7 lo mismo que restar d , que es la operación deseada. Por lo tanto, nuevamente, hacemos la resta sumando bajo aritmética módulo. En total, la variable e contiene el paso desde el día después del día de la luna llena hasta el domingo siguiente más cercano, entre 0 y 6 días adelante. La constante N proporciona el punto de partida para los cálculos para cada siglo y depende de dónde se ubicaba implícitamente el 1 de enero del año 1 cuando se construyó el calendario gregoriano.
La expresión d + e puede dar como resultado desfases en el rango de 0 a 35 que apuntan a posibles domingos de Pascua del 22 de marzo al 26 de abril. Por razones de compatibilidad histórica, todos los desfases de 35 y algunos de 34 se restan por 7, saltando un domingo hacia atrás hasta el día de la luna llena (en efecto, utilizando un e negativo de −1). Esto significa que el 26 de abril nunca es Domingo de Pascua y que el 19 de abril está sobrerrepresentado. Estas últimas correcciones son solo por razones históricas y no tienen nada que ver con el algoritmo matemático. El desfase de 34 se ajusta si (y solo si) d = 28 y d = 29 en otro lugar del ciclo de 19 años.
El uso del algoritmo de Pascua de Gauss para los años anteriores a 1583 carece de sentido desde el punto de vista histórico, ya que antes de ese año no se utilizaba el calendario gregoriano para determinar la Pascua. El uso del algoritmo en el futuro lejano es cuestionable, ya que no sabemos nada sobre cómo definirán las distintas iglesias la Pascua en el futuro. Los cálculos de la Pascua se basan en acuerdos y convenciones, no en los movimientos celestiales reales ni en hechos históricos indiscutibles.
Algoritmo gregoriano anónimo
| Dividendo | Divisor | Cociente | Resto |
|---|---|---|---|
| año | 19 | — | a |
| año | 100 | b | do |
| b | 4 | d | mi |
| b +8 | 25 | F | — |
| b - f +1 | 3 | gramo | — |
| 19 a + b − d − g + 15 | 30 | — | yo |
| do | 4 | i | a |
| 32 + 2 e + 2 i − h − k | 7 | — | yo |
| a + 11 h + 22 l | 451 | metro | — |
| h + l − 7 m + 114 | 31 | norte | o |
"Un corresponsal de Nueva York" presentó este algoritmo para determinar la Pascua gregoriana a la revista Nature en 1876. [74] [75] Ha sido reimpreso muchas veces, por ejemplo, en 1877 por Samuel Butcher en The Ecclesiastical Calendar , [76] en 1916 por Arthur Downing en The Observatory , [77] en 1922 por H. Spencer Jones en General Astronomy , [78] en 1977 por el Journal of the British Astronomical Association , [79] en 1977 por The Old Farmer's Almanac , en 1988 por Peter Duffett-Smith en Practical Astronomy with your Calculator , y en 1991 por Jean Meeus en Astronomical Algorithms . [80] Debido a la cita del libro de Meeus, este algoritmo también se llama "Meeus/Jones/Butcher":
| Variable | Expresión | Y = 1961 | 2024 | 2025 |
|---|---|---|---|---|
| a = | Y mod 19 | 4 | 10 | 11 |
| b = | ⌊ Y/100 ⌋ | 19 | 20 | 20 |
| c = | Y mod 100 | 61 | 24 | 25 |
| d = | ⌊ b/4 ⌋ | 4 | 5 | 5 |
| mi = | b módulo 4 | 3 | 0 | 0 |
| f = | ⌊ b +8/25 ⌋ | 1 | 1 | 1 |
| sol = | ⌊ b - f +1/3 ⌋ | 6 | 6 | 6 |
| h = | (19a + b - d - g + 15)mód 30 | 10 | 4 | 23 |
| yo = | ⌊ do/4 ⌋ | 15 | 6 | 6 |
| k = | c módulo 4 | 1 | 0 | 1 |
| yo = | (32 + 2 mi + 2 yo − h − k ) mod 7 | 1 | 5 | 6 |
| m = | ⌊ a + 11 h + 22 l/451 ⌋ | 0 | 0 | 0 |
| h + l − 7m + 114 | 125 | 123 | 143 | |
| n = | ⌊ h + l − 7 m + 114/31 ⌋ | 4 | 3 | 4 |
| o = | ( h + l − 7 m + 114) módulo 31 | 1 | 30 | 19 |
| Pascua gregoriana | 2 de abril de 1961 | 31 de marzo de 2024 | 20 de abril de 2025 | |
En este algoritmo, la variable n indica el mes del año (ya sea marzo para n = 3, o abril para n = 4), mientras que el día del mes se obtiene como ( o + 1). En 1961, New Scientist publicó una versión del algoritmo de Nature que incorporaba algunos cambios. [81] La variable g se calculó utilizando la corrección de Gauss de 1816, lo que dio como resultado la eliminación de la variable f . Algunos resultados de ordenamiento dan como resultado el reemplazo de la variable o (a la que se debe agregar uno para obtener la fecha de Pascua) con la variable p , que da la fecha directamente.
| Variable | Expresión | Y = 1961 | 2024 | 2025 |
|---|---|---|---|---|
| F | — | — | — | |
| sol = | ⌊ 8b + 13/25 ⌋ | 6 | 6 | 6 |
| m = | ⌊ a + 11 h + 19 l/433 ⌋ | 0 | 0 | 0 |
| n = | ⌊ h + l − 7 m + 90/25 ⌋ | 4 | 3 | 4 |
| o | — | — | — | — |
| p = | ( h + l − 7 m + 33 n + 19) módulo 32 | 2 | 31 | 20 |
| Pascua gregoriana | 2 de abril de 1961 | 31 de marzo de 2024 | 20 de abril de 2025 | |
Algoritmo juliano de Meeus
Jean Meeus, en su libro Astronomical Algorithms (1991, p. 69), presenta el siguiente algoritmo para calcular la Pascua juliana en el Calendario Juliano, que no es el Calendario Gregoriano utilizado como calendario civil en la mayor parte del mundo contemporáneo. Para obtener la fecha de la Pascua Ortodoxa Oriental en este último calendario, se deben agregar 13 días (desde 1900 hasta 2099) a las fechas julianas, lo que produce las fechas que aparecen a continuación, en la última fila. (Hasta el año 2099 d. C., el 21 de marzo juliano equivale al 3 de abril gregoriano).
| Variable | Expresión | Y = 2008 | 2009 | 2010 | 2011 | 2016 | 2024 | 2025 |
|---|---|---|---|---|---|---|---|---|
| a = | Y módulo 4 | 0 | 1 | 2 | 3 | 0 | 0 | 1 |
| b = | Y mod 7 | 6 | 0 | 1 | 2 | 0 | 1 | 2 |
| c = | Y mod 19 | 13 | 14 | 15 | 16 | 2 | 10 | 11 |
| d = | (19 c + 15) mod 30 | 22 | 11 | 0 | 19 | 23 | 25 | 14 |
| mi = | ( 2a + 4b − d + 34) módulo 7 | 1 | 4 | 0 | 1 | 4 | 6 | 2 |
| re + mi + 114 | 137 | 129 | 114 | 134 | 141 | 145 | 130 | |
| mes = | ⌊ re + mi + 114/31 ⌋ | 4 | 4 | 3 | 4 | 4 | 4 | 4 |
| día = | (( d + e +114)mód 31)+1 | 14 | 6 | 22 | 11 | 18 | 22 | 7 |
| Día de Pascua (calendario juliano) | 14 de abril de 2008 | 6 de abril de 2009 | 22 de marzo de 2010 | 11 de abril de 2011 | 18 de abril de 2016 | 22 de abril de 2024 | 7 de abril de 2025 | |
| Equivalente del calendario gregoriano | 27 de abril de 2008 | 19 de abril de 2009 | 4 de abril de 2010 | 24 de abril de 2011 | 1 de mayo de 2016 | 5 de mayo de 2024 | 20 de abril de 2025 | |
Véase también
- Christian Zeller – matemático alemán
- Crucifixión en la oscuridad – Episodio del evangelio cristiano sobre el cielo oscurecido
- Reforma de la fecha de la Semana Santa – Propuestas para cambiar la fecha de la festividad
Referencias
Notas
- ^ Aunque ésta es la datación de Augustalis de Bruno Krusch, véanse los argumentos a favor de una fecha del siglo V en Mosshammer 2008, pp. 217, 227-228.
- ^ El ciclo lunar de Anatolio, según las tablas del De ratione paschali , incluía sólo dos años bisiestos cada 19 años, por lo que no podía ser utilizado por nadie que utilizara el calendario juliano, que tenía cuatro o cinco años bisiestos por ciclo lunar. [14] [15]
- ^ Para confirmar el papel de Dionisio, véase Blackburn y Holford-Strevens 1999, pág. 794.
- ^ Por ejemplo, en el calendario juliano, en Roma en 1550, el equinoccio de marzo ocurrió el 11 de marzo a las 6:51 am hora media local . [28]
- ^ Aunque antes del reemplazo del calendario juliano en 1752 algunos impresores del Libro de Oración Común colocaron el saltus correctamente, comenzando el mes siguiente el 30 de julio, ninguno de ellos continuó la secuencia correctamente hasta el final del año.
- ^ Aunque antes del reemplazo del calendario juliano en 1752 algunos impresores del Libro de Oración Común colocaron el saltus correctamente, comenzando el mes siguiente el 30 de julio, ninguno de ellos continuó la secuencia correctamente hasta el final del año.
- ^ "El [Número Áureo] de un año d.C. se obtiene sumando uno, dividiendo por 19 y tomando el resto (tratando 0 como 19)". (Blackburn y Holford-Strevens 1999, pág. 810).
- ^ Véase especialmente el primer, segundo, cuarto y sexto canon, y el calendarium
- ^ Se puede verificar utilizando Blackburn & Holford-Strevens 1999, pág. 825, Tabla 7.
- ^ En 2004 y nuevamente en 2015 hay lunas llenas los días 2 y 31 de julio.
- ^ Tradicionalmente, en el Occidente cristiano, esta situación se solucionaba ampliando el primer mes lunar de 29 días del año a 30 días, y comenzando el mes lunar siguiente un día más tarde si debía comenzar antes del día bisiesto. (Blackburn y Holford-Strevens 1999, p. 813).
- ^ El Expl.Suppl. de 2013 en la p.599 especifica en cambio 70.499.175 lunaciones, sin explicación ni referencia. Este número parece ser el valor truncado de dividir 2.081.882.250 días por 29,53059, que es un valor redondeado para la duración de la lunación que se encuentra en la tabla en la parte superior de la p.587. Por lo tanto, el número de 70.499.175 sería una estimación del número real de lunaciones en un período de 5,7 millones de años, y no el número de lunas nuevas realmente contabilizadas por el calendario lunar gregoriano a lo largo de su ciclo completo.
Citas
- ^ Ayto 2009, pág. 123.
- ^ Peterson 2015, pág. 468.
- ^ Beda 1999, pág. xviii.
- ^ Beda 1999, págs. xviii–xx.
- ^ Juan 19:14
- ^ Beda 1999, pág. xx.
- ^ Beda 1999, pág. xxxvi.
- ^ Bede 1999, págs. 425–426, Apéndice 4: Una nota sobre el término computus.
- ^ Éxodo 12:18
- ^ Levítico 23:5
- ^ Beda 1999, págs. xxxv-xxxvii.
- ^ Anatolio, Libro 7, Capítulo 33.
- ^ Beda 1999, págs. xxxviii – xl.
- ^ Turner 1895, págs. 699–710.
- ^ McCarthy 1996, págs. 285–320.
- ^ Declercq 2000, pág. 80.
- ^ Declercq 2000, pág. 97.
- ^ Declercq 2000, pág. 99.
- ↑ Audette, Rodolphe (9 de diciembre de 2007). «Dionysius Exiguus – Liber de Paschate». Archivado desde el original el 15 de abril de 2021. Consultado el 26 de junio de 2021 .
- ^ Blackburn y Holford-Strevens 1999, pág. 793.
- ^ McCarthy 1993, págs. 204-224.
- ^ Beda 1907, p. 193, Libro III, Capítulo XXV.
- ^ Bede 1943, p. 90: La carta [de Cummiano] es a la vez un informe y una disculpa o justificación al abad Seghine en Iona sobre un sínodo celebrado en Campus Lenis (Magh-Lene), donde se consideró la cuestión de la Pascua. El resultado directo del sínodo fue una alteración de la observancia entre los irlandeses del sur y la adopción del cómputo alejandrino.
- ^ Beda 1907, pág. xxvii.
- ^ Beda 1999, págs. lix–lxiii.
- ^ Kekis, Theoharis. "El calendario de la Iglesia Ortodoxa" (PDF) . Red de Acción de Chipre de América. Archivado desde el original (PDF) el 26 de noviembre de 2012. Consultado el 11 de marzo de 2012 .
- ^ Torre de la canción de Re-vision Radio. "Las muchas Pascuas y Eostres para muchos: una elección de aleluyas". Archivado desde el original el 16 de abril de 2021 . Consultado el 26 de junio de 2021 .
- ^ "Calculadora de estaciones". Hora y fecha AS . 2014. Archivado desde el original el 23 de marzo de 2019 . Consultado el 23 de marzo de 2019 .
- ^ abc de Gante 2019.
- ^ Shields 1924, págs. 407–411.
- ^ Hacia una fecha común para la Pascua, Alepo, Siria: Consulta del Consejo Mundial de Iglesias y el Consejo de Iglesias del Oriente Medio, 10 de marzo de 1997, archivado desde el original el 30 de marzo de 2018.
- ^ Richards 2013, p. 587: El día consta de 86.400 segundos SI , y se da el mismo valor para los años 500, 1000, 1500 y 2000.
- ^ ἐπακτός. Liddell, Henry George ; Scott, Robert ; Un léxico griego-inglés en el Proyecto Perseo .
- ^ Harper, Douglas. "epact". Diccionario Etimológico en Línea .
- ^ HM Nautical Almanac Office (1974). Suplemento explicativo de las efemérides astronómicas. Londres. pág. 422.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Beda 1999, págs. xlvi.
- ^ Clavio 1603.
- ^ Dershowitz y Reingold 2008, págs. 113-117.
- ^ Mosshammer 2008, pág. 76.
- ^ Dershowitz y Reingold 2008, págs. 114-115.
- ^ Dershowitz y Reingold 2008, pág. 114.
- ^ Grotefend 1891.
- ^ Ginzel 1914.
- ^ Weisstein (c. 2006) "Luna llena pascual" concuerda con esta línea de tabla hasta 2009.
- ^ abcdef Davison, Michael E. (1980). «The Frequency Distribution of the Dates of Easter» (La distribución de frecuencias de las fechas de Pascua). The Irish Astronomical Journal . 14 : 156–164. Código Bibliográfico :1980IrAJ...14..156D. Archivado desde el original el 9 de abril de 2023 . Consultado el 17 de mayo de 2022 .
- ^ Dershowitz y Reingold 2008, pág. 117.
- ^ Walker, George W. (1944). «Raras fechas de Pascua». Astronomía popular . N.º 52. págs. 139–142. Código Bibliográfico :1944PA.....52..139W. Archivado desde el original el 9 de abril de 2023. Consultado el 17 de mayo de 2022 .
- ^ Roegel, Denis (24 de noviembre de 2004). «La luna nueva que falta en el año 16399 d. C. y otras anomalías del calendario gregoriano» (PDF) . Archivado (PDF) del original el 25 de febrero de 2021. Consultado el 26 de junio de 2021 .
- ^ Paucker, Georg (1837). "Die Osterrechnung oder Vorschlag zur Einführung eines kirchlichen Kalenders und Osterkanons". Riga: Buchhandlung de Eduard Frantzen. pag. 59. Archivado desde el original el 9 de abril de 2023 . Consultado el 6 de septiembre de 2022 .
- ^ "Almanaque y efemérides astronómicas del año 1931". Londres: His Majesty's Stationery Office. 1929.
- ^ Doggett, LE (1992). Seidelmann, P. Kenneth (ed.). Suplemento explicativo del Almanaque astronómico. Washington: Observatorio Naval de los Estados Unidos. pág. 582. ISBN 0-935702-68-7.
- ^ de Kort 1949, págs. 109-116.
- ^ Swerdlow 1986, págs. 109-118.
- ^ "La duración de las estaciones". Universidad de Toronto . Canadá. Archivado desde el original el 20 de enero de 2018. Consultado el 31 de enero de 2018 .
- ^ "Duración media del año equinoccial hacia el norte" (PDF) . U. Toronto . Canadá. Archivado (PDF) del original el 5 de marzo de 2016 . Consultado el 31 de enero de 2018 .
- ^ Ley para regular el comienzo del año y corregir el calendario actualmente en uso Estatutos generales 1765, con tablas de Pascua
- ^ Libro de oración común y administración de los sacramentos y otros ritos y ceremonias de la Iglesia. Joseph Bentham. 9 de agosto de 1765. Consultado el 9 de agosto de 2017 a través de Internet Archive.
- ^ Libro de Oración Común. «Tablas y Reglas». Archivado desde el original el 27 de mayo de 2021. Consultado el 26 de junio de 2021 .
- ^ Stockton, JR "El cálculo del Domingo de Pascua según el Libro de Oración Común". Archivado desde el original el 7 de septiembre de 2015 . Consultado el 9 de agosto de 2017 .
- ↑ Papa Gregorio XIII (24 de febrero de 1582). «Inter Gravissimas». Archivado desde el original el 13 de febrero de 2006. Consultado el 9 de agosto de 2017 .
- ^ Teres 1984, pág. 178.
- ^ Schaff, Philip; Wace, Henry, eds. (1890), La carta sinodal, Padres de Nicea y Post-Nicea: Segunda serie, vol. 14, Los siete concilios ecuménicos, Grand Rapids, Michigan , EE. UU.: Eerdmans Pub Co., págs. 112-114, ISBN 0-8028-8129-7, archivado del original el 28 de septiembre de 2020 , consultado el 4 de julio de 2020
- ^ Grumel 1958, pág. 36.
- ^ Grumel 1958, pág. 48.
- ^ Byrhtferth de Ramsey 1995, págs. 136–7, 320–322.
- ^ Domus Quaedam Vetus 2009, pag. 151.
- ^ Beda 1999, págs. xlvii.
- ^ desde Nothaft 2018, págs. 275–277.
- ^ abcde Lange 1928.
- ^ abc Zeyer 2020, págs. 5-10.
- ^ "Gauß-CD". webdoc.sub.gwdg.de . Archivado desde el original el 6 de diciembre de 2016 . Consultado el 9 de agosto de 2017 .
- ^ Kothe, Jochen. "Berechnung des Osterfestes". Astronomische Abhandlungen [ Tratados astronómicos ] (en alemán). Archivado desde el original el 9 de julio de 2012 . Consultado el 9 de agosto de 2017 .
- ^ Kothe, Jochen. "Berichtigung ze dem aufsatze". Astronomische Abhandlungen [ Tratados astronómicos ] (en alemán). Archivado desde el original el 12 de julio de 2012 . Consultado el 9 de agosto de 2017 .
- ^ ab Bien 2004, págs.
- ^ Un corresponsal de Nueva York (20 de abril de 1876). "Para encontrar la Pascua". Nature : 487.
{{cite journal}}:|author=tiene nombre genérico ( ayuda ) - ^ Carnicero 1877, pág. 225.
- ^ Downing 1916, págs. 215-219.
- ^ Spencer Jones 1922, pág. 73.
- ^ "Cartas al editor". Revista de la Asociación Astronómica Británica . 88 : 91. Diciembre de 1977. Código Bibliográfico :1977JBAA...88...87.
- ^ Meeus 1991, págs. 67–68.
- ^ O'Beirne 1961, pág. 828.
Fuentes
- Anatolio de Laodicea , "Cánones pascuales citados por Eusebio", Historia eclesiástica de Eusebio , archivado del original el 14 de abril de 2021 , consultado el 13 de abril de 2021.
- Ayto, John, ed. (2009). Oxford Dictionary of English Idioms (3.ª ed.). OUP Oxford. pág. 123. ISBN 978-0-19-954378-6.
- Beda (1907) [731]. Historia eclesiástica de Inglaterra de Beda. Traducido por Sellar, AM; Giles, JA Londres: George Bell and Sons. Archivado desde el original el 12 de mayo de 2019. Consultado el 23 de marzo de 2019 a través del Proyecto Gutenberg .
- Beda (1943). Charles Williams Jones (ed.). Bedae Opera de Temporibus. Academia Medieval de América. Archivado desde el original el 9 de abril de 2023. Consultado el 9 de junio de 2021 .
- Bede (1999). El cálculo del tiempo. Traducido por Faith Wallis. Liverpool University Press. ISBN 978-0-85323-693-1Archivado desde el original el 9 de abril de 2023 . Consultado el 11 de marzo de 2016 .
- Bien, Reinhold (julio de 2004). "Gauß y más allá: la creación de algoritmos de Pascua". Archivo de Historia de las Ciencias Exactas . 58 (5): 439−452. Bibcode :2004AHES...58..439B. doi :10.1007/s00407-004-0078-5. S2CID 121657716.
- Blackburn, Bonnie J.; Holford-Strevens, Leofranc (1999). El compañero de Oxford para el año. Oxford University Press. ISBN 978-0-19-214231-3.
- Butcher, Samuel (1877). El calendario eclesiástico: su teoría y construcción. Dublín: Hodges, Foster y Figgis. Archivado desde el original el 9 de abril de 2023. Consultado el 11 de marzo de 2016 .
- Byrhtferth de Ramsey (1995). Lapidge, Michael; Peter Stuart Baker (eds.). Enchiridion de Byrhtferth. Sociedad de textos en inglés temprano. ISBN 978-0-19-722416-8Archivado desde el original el 9 de abril de 2023 . Consultado el 9 de junio de 2021 .
- Clavio, Cristóbal (1603). Calendario romaní de Gregorio XIII. PM restituti explicatio. Archivado desde el original el 9 de abril de 2023 . Consultado el 16 de noviembre de 2021 .En el quinto volumen de Opera Mathematica, Maguncia, 1612. Opera Mathematica de Christoph Clavius incluye imágenes de página de los Seis Cánones y la Explicatio (Ir a la página: Calendario romano de Gregorio XIII).
- Constantino el Grande, emperador (325): Carta a los obispos que no asistieron al primer Concilio de Nicea; de la Vita Constantini de Eusebio . Traducciones al inglés: Documentos del Primer Concilio de Nicea, "Sobre la celebración de la Pascua" (cerca del final) Archivado el 27 de enero de 2013 en Wayback Machine y Eusebio, Vida de Constantino, Libro III, Capítulos XVIII-XIX Archivado el 16 de septiembre de 2009 en Wayback Machine
- de Kort, JJMA (septiembre de 1949). "Apreciación astronómica del calendario gregoriano". Ricerche Astronomiche . 2 (6): 109–116. Código bibliográfico : 1949RA......2..109D.
- Declercq, Georges (2000). Anno Domini: Los orígenes de la era cristiana. Isd. ISBN 978-2-503-51050-7Archivado del original el 9 de abril de 2023 . Consultado el 14 de diciembre de 2020 .
- Dershowitz, Nachum ; Reingold, Edward M. (2008). Cálculos calendáricos. Cambridge University Press. ISBN 978-0-521-88540-9Archivado del original el 9 de abril de 2023 . Consultado el 14 de diciembre de 2020 .
- Dionisio el Exiguo (525): Liber de Paschate . En línea: (texto completo en latín) Archivado el 3 de junio de 2008 en Wayback Machine y (tabla con Argumenta en latín, con traducción al inglés)
- Domus Quaedam Vetus (julio de 2009). Carmina Medii Aevi Maximam Partem Inedita. BiblioBazar. ISBN 978-1-110-75828-9.
- Downing, AMW (mayo de 1916). «La fecha de Pascua». The Observatory . 39 : 215–219. Bibcode :1916Obs....39..215D.
- Eusebio de Cesarea, Historia de la Iglesia , Traducido por GA Williamson. Revisado y editado con una nueva introducción de Andrew Louth. Penguin Books, Londres, 1989.
- Gregorio XIII (Papa) y el comité de reforma del calendario (1581): la bula papal Inter Gravissimas y los seis cánones. En línea en: "Les textes fondateurs du calendrier grégorien" Archivado el 29 de abril de 2012 en Wayback Machine , con algunas partes de la Explicatio de Clavius .
- van Gent, Robert (2019), Fechas anómalas del Domingo de Pascua en el siglo XVIII y principios del XIX, Universidad de Utrecht, archivado del original el 1 de agosto de 2020 , consultado el 23 de julio de 2019.
- Ginzel, Friedrich Karl (1914). Handbuch der mathematischen und technischen Chronologie, Banda III . Leipzig, Alemania: Hinrichs.
- Grotefend, Hermann (1891). Zeitrechnung des deutschen Mittelalters und der Neuzeit. Hahn. Archivado desde el original el 9 de abril de 2023 . Consultado el 27 de noviembre de 2020 .
- Grumel, V. (1958). La cronología (en francés). París: Presses Universitaires de France. OCLC 4260118.
- Lange, Ludwig (1928). "Paradoja" Osterdaten im Gregorianischen Kalender und ihre Bedeutung für die moderne Kalender reform von Ludwig Lange. Vorgelegt von Eduard Schwartz el 7 de julio de 1928. Bayer. Akád. d. Wissenschaften. Archivado desde el original el 9 de abril de 2023 . Consultado el 27 de noviembre de 2020 .
- Lichtenberg, Heiner (2003). "Das anpassbar zyklische, solilunare Zeitzählungssystem des gregorianischen Kalenders". Mathematische Semesterberichte . 50 : 45–76. doi :10.1007/s00591-003-0063-0. S2CID 120639320.
- McCarthy, Daniel (agosto de 1993). "Principios de Pascua y un ciclo lunar del siglo V utilizado en las Islas Británicas". Revista de Historia de la Astronomía . 24 (3): 204–224. Bibcode :1993JHA....24..204M. doi :10.1177/002182869302400304. S2CID 115765809.
- McCarthy, Daniel (1996). "Las tablas lunares y pascuales de De ratione paschali atribuidas a Anatolio de Laodicea". Archivo de Historia de las Ciencias Exactas . 49 (4): 285–320. Bibcode :1996AHES...49..285M. doi :10.1007/bf00374701. S2CID 120081352.
- Meeus, Jean (1991). Algoritmos astronómicos . Richmond, Virginia: Willmann-Bell.
- Mosshammer, Alden A. (2008). El Cómputo de Pascua y los orígenes de la era cristiana. Oxford: University Press. ISBN 978-0-19-954312-0Archivado desde el original el 9 de abril de 2023 . Consultado el 9 de junio de 2021 .
- Nothaft, C. Philipp E. (2018). Error escandaloso: reforma del calendario y astronomía calendárica en la Europa medieval. Oxford University Press. ISBN 978-0-19-879955-9Archivado del original el 9 de abril de 2023 . Consultado el 27 de noviembre de 2020 .
- O'Beirne, TH (30 de marzo de 1961). «Cómo diez divisiones conducen a la Pascua». New Scientist . 9 (228): 828. Archivado desde el original el 9 de abril de 2023 . Consultado el 7 de junio de 2021 .
- Peterson, Michael D. (2015). "El ayuno: cristiano oriental". En Johnston, William M.; Kleinhenz, Christopher (eds.). Enciclopedia del monacato. Routledge. pág. 468. ISBN 978-1-57958-090-2Archivado desde el original el 9 de abril de 2023 . Consultado el 21 de marzo de 2023 .
- Richards, EG (2013). "Calendarios". En SE Urban; PK Seidelmann (eds.). Suplemento explicativo del Almanaque Astronómico (3.ª ed.). Mill Valley, CA: Univ Science Books.
- Swerdlow, Noel M. (1986). "La duración del año en la propuesta original para el calendario gregoriano". Revista de Historia de la Astronomía . 17 (49): 109–118. Bibcode :1986JHA....17..109S. doi :10.1177/002182868601700204. S2CID 118491152.
- Shields, Miriam Nancy (1924). "El nuevo calendario de las iglesias orientales". Astronomía popular . 32 : 407–411. Código Bibliográfico :1924PA.....32..407S.
- Spencer Jones, H. (1922). Astronomía general. Londres: Longsman, Green.
- Teres, Gustav (1984). "Cálculos del tiempo y Dionysius Exiguus". Revista de Historia de la Astronomía . 15 (3): 177–188. Código Bib : 1984JHA....15..177T. doi :10.1177/002182868401500302. S2CID 117094612.
- Turner, CH (1895). "El canon pascual de Anatolio de Laodicea". The English Historical Review . 10 : 699–710. doi :10.1093/ehr/x.xl.699.
- Wheatly, Charles (1871) [1710]. Una ilustración racional del Libro de Oración Común de la Iglesia de Inglaterra. Londres: Bell and Daldy.
- Zeyer, KlausPeter (2020). "Häufigkeit von Osterparadoxien: Negativo Äquinoktialparadoxien der Jahre 2353 und 2372 als seltenste Variante". Regiomontanusbote . 33 : 5–10.
Lectura adicional
- Borst, Arno (1993). El ordenamiento del tiempo: desde el cómputo antiguo hasta la traducción al inglés moderna de Andrew Winnard. Cambridge: Polity Press; Chicago: Univ. of Chicago Press.
- Coyne, GV, MA Hoskin, MA, y Pedersen, O. (ed.) Reforma gregoriana del calendario: Actas de la conferencia del Vaticano para conmemorar su 400 aniversario, 1582–1982 Archivado el 18 de agosto de 2007 en Wayback Machine , (Ciudad del Vaticano: Academia Pontificia de las Ciencias, Specolo Vaticano, 1983).
- Gibson, Margaret Dunlop, La Didascalia Apostolorum en siríaco , Cambridge University Press, Londres, 1903.
- Schwartz, E., Christliche und jüdische Ostertafeln , (Abhandlungen der königlichen Gesellschaft der Wissenschaften zu Göttingen. Pilologisch-historische Klasse. Neue Folge, Band viii.) Weidmannsche Buchhandlung , Berlín, 1905.
- Philip Schaff (ed.) Teodoreto, Jerónimo, Genadio y Rufinio: escritos históricos Archivado el 15 de mayo de 2019 en Wayback Machine.
- Stern, Sacha, Calendario y comunidad: una historia del calendario judío del siglo II a. C. al siglo X d. C. , Oxford University Press, Oxford, 2001.
- Walker, George W, Intervalos de Pascua Archivado el 17 de mayo de 2022 en Wayback Machine , Popular Astronomy, abril de 1945, vol. 53, págs. 162-179.
- Walker, George W, Intervalos de Pascua Archivado el 17 de mayo de 2022 en Wayback Machine. (Continuación), Popular Astronomy, mayo de 1945, vol. 53, págs. 218-232.
- Weisstein, Eric. (c. 2006) "Luna llena pascual" en Mundo de la astronomía .
Enlaces externos
- Fórmulas y funciones de la hoja de cálculo de Excel para calcular la Pascua
- Las obras completas del Venerable Beda vol. 6 (Contiene De Temporibus y De Temporum ratione ).
- La entrada sobre epactos en la Enciclopedia Católica de 1911
- Los textos originales de la reforma del calendario gregoriano (en latín), con traducciones al francés de Rodolphe Audette
- Una calculadora de Pascua con una extensa bibliografía y enlaces útiles
- Sitio de efemérides de la Oficina de Longitudes con calculadora de Pascua (válida entre 325 y 2500)
- Una página de calendario y calculadora de Holger Oertel
- Una página de Clive Feather con una breve explicación, algunas tablas más y otro algoritmo.
- (en alemán) Un sitio web completo sobre calendarios y calculadora de calendarios y Pascuas de Nikolaus A. Bär Archivado el 6 de septiembre de 2003 en Wayback Machine.
- Explicación del calendario solar y lunar gregoriano, con procedimientos mejorados respecto al método tabular, por David Madore
- Mesa de Pascua de Dionisio el Exiguo
- Diagramas de cálculo mnemotécnico de manos del manuscrito de la Biblioteca Británica
- St. Gallen, Stiftsbibliothek, Codex Sangallensis 378 (siglo XI) p. 28. Contiene el poema Nonae Aprilis norunt quinos.
- Un método simplificado para determinar la fecha de Pascua para todos los años del 326 al 4099 por Ronald W. Mallen
- Texto de la Ley de Calendario (Nuevo Estilo) de 1750, Ley del Parlamento británico que introdujo el Calendario Gregoriano con las modificaciones realizadas hasta la fecha. Contiene tablas para calcular la Pascua hasta el año 8599. Compárese con la Ley tal como se aprobó.
- Computuslat Una base de datos de manuscritos medievales que contiene algoritmos computacionales, textos, tablas, diagramas y calendarios en latín.


