Torneo de todos contra todos
Un torneo de todos contra todos o torneo de todos contra todos es un formato de competencia en el que cada concursante se enfrenta a todos los demás participantes, generalmente por turno. [1] [2] Un torneo de todos contra todos contrasta con un torneo de eliminación , en el que los participantes son eliminados después de una cierta cantidad de victorias o derrotas.
Terminología
El término round-robin se deriva del término francés ruban ('cinta'). Con el tiempo, el término se transformó en robin . [3] [4]
En un sistema de todos contra todos , cada participante juega una vez con todos los demás participantes. Si cada participante juega con todos los demás dos veces, esto se denomina con frecuencia doble round-robin . El término rara vez se utiliza cuando todos los participantes juegan entre sí más de dos veces, [1] y nunca se utiliza cuando un participante juega con otros un número desigual de veces, como es el caso en casi todas las principales ligas deportivas profesionales de América del Norte.
En el Reino Unido , un torneo de todos contra todos se ha denominado torneo americano en deportes como el tenis o el billar, que normalmente tienen torneos de eliminación simple (o "knockout"), aunque ahora esto rara vez se hace. [5] [6] [7]
Un torneo de todos contra todos con cuatro jugadores a veces se denomina "quad" o "foursome". [8]
Aplicaciones
En los deportes con un gran número de partidos competitivos por temporada, los torneos de todos contra todos son comunes. La mayoría de las ligas de fútbol del mundo se organizan con un sistema de todos contra todos, en el que cada equipo juega contra todos los demás de su liga una vez en casa y otra fuera. Este sistema también se utiliza en la clasificación para los principales torneos, como la Copa Mundial de la FIFA y los torneos continentales (por ejemplo , la Eurocopa de la UEFA , la Copa de Oro de la CONCACAF , la Copa Asiática de la AFC , la Copa América de la CONMEBOL y la Copa de Naciones de la CAF ). También hay torneos de todos contra todos de bridge , ajedrez , damas , go , hockey sobre hielo , curling y Scrabble . El Campeonato Mundial de Ajedrez decidió en 2005 y en 2007 un torneo de todos contra todos con ocho jugadores, en el que cada jugador se enfrenta a todos los demás jugadores una vez con las blancas y otra con las negras.
En un ejemplo más extremo, la Liga KBO de béisbol juega un sistema de todos contra todos de 16 partidos, en el que cada uno de los 10 equipos juega entre sí 16 veces, para un total de 144 juegos por equipo.
La LIDOM (Liga Invernal de Béisbol de la República Dominicana) juega un torneo semifinal a 18 rondas entre cuatro equipos clasificados.
Las clasificaciones de los torneos grupales generalmente se basan en el número de partidos ganados y empatados, con una variedad de criterios de desempate.
Con frecuencia, las fases de grupos dentro de un torneo más amplio se llevan a cabo con un sistema de todos contra todos. Los ejemplos con una programación de todos contra todos incluyen la Copa Mundial de la FIFA , el Campeonato Europeo de Fútbol de la UEFA y la Copa de la UEFA (2004-2009) en fútbol, el Super Rugby ( rugby union ) en el hemisferio sur durante sus iteraciones pasadas como Super 12 y Super 14 (pero no en sus formatos posteriores de 15 y 18 equipos), la Copa Mundial de Críquet junto con la Premier League india , el importante torneo Twenty-20 Cricket y muchas conferencias universitarias de fútbol americano , como la Conference USA (que actualmente tiene 9 miembros). Las fases de grupos de las competiciones de clubes de la UEFA y la Copa Libertadores se disputan como un sistema de todos contra todos, al igual que la mayoría de las ligas de baloncesto fuera de los Estados Unidos, incluida la temporada regular de la Euroliga (así como su antigua fase Top 16); la United Football League ha utilizado un sistema de todos contra todos doble para sus temporadas de 2009 y 2010 .
Los torneos de tenis de final de temporada también utilizan un formato de todos contra todos antes de las etapas de semifinales.
Evaluación
Esta sección necesita citas adicionales para su verificación . ( Marzo de 2022 ) |
Ventajas
El campeón de un torneo todos contra todos es el concursante que gana más juegos, excepto cuando es posible que haya empates.
En teoría, un torneo de todos contra todos es la forma más justa de determinar al campeón entre un número conocido y fijo de participantes. Cada participante, ya sea jugador o equipo, tiene las mismas posibilidades contra todos los demás oponentes porque no hay una clasificación previa de los participantes que impida un enfrentamiento entre una pareja determinada. Se considera que el elemento de suerte es menor en comparación con un sistema de eliminación directa, ya que una o dos malas actuaciones no tienen por qué arruinar la posibilidad de un competidor de obtener la victoria final. Los registros finales de los participantes son más precisos, en el sentido de que representan los resultados durante un período más largo contra el mismo oponente.
El sistema también es mejor para clasificar a todos los participantes, no solo para determinar al ganador. Esto es útil para determinar la clasificación final de todos los competidores, del más fuerte al más débil, a los efectos de la clasificación para otra etapa o competencia, así como para los premios en efectivo.
En los deportes de equipo, los campeones de las grandes ligas en formato de todos contra todos son generalmente considerados el "mejor" equipo del país, en lugar de los ganadores de la copa, cuyos torneos suelen seguir un formato de eliminación simple.
Además, en torneos como las Copas Mundiales de la FIFA o la ICC, una primera ronda que consiste en una serie de mini round robins entre grupos de 4 equipos evita la posibilidad de que un equipo viaje miles de kilómetros para ser eliminado después de una sola mala actuación en un sistema de eliminación directa. Los primeros uno, dos o, en ocasiones, tres equipos de estos grupos pasan entonces a una etapa de eliminación directa para el resto del torneo.
En el círculo de la muerte es posible que no surja ningún campeón de un torneo de todos contra todos, incluso si no hay sorteo, pero la mayoría de los deportes tienen sistemas de desempate que resuelven esto.
Desventajas
Los torneos de todos contra todos pueden resultar demasiado largos en comparación con otros tipos de torneos y los partidos programados más tarde pueden no tener una importancia sustancial. También pueden requerir procedimientos de desempate.
Los torneos del sistema suizo intentan combinar elementos de los formatos de todos contra todos y de eliminación, para proporcionar un campeón digno utilizando menos rondas que un sistema de todos contra todos, pero permitiendo empates y derrotas.
Duración del torneo
La principal desventaja de un torneo de todos contra todos es el tiempo necesario para completarlo. A diferencia de un torneo de eliminación directa, en el que se elimina a la mitad de los participantes después de cada ronda, un torneo de todos contra todos requiere una ronda menos que el número de participantes. Por ejemplo, un torneo de 16 equipos se puede completar en solo 4 rondas (es decir, 15 partidos) en un formato de eliminación directa; un formato de torneo de doble eliminación requiere 30 (o 31) partidos, pero un torneo de todos contra todos requeriría 15 rondas (es decir, 120 partidos) para finalizar si cada competidor se enfrenta una vez.
Otros problemas surgen de la diferencia entre la equidad teórica del formato de todos contra todos y la práctica en un evento real. Dado que el vencedor se va eligiendo gradualmente a través de múltiples rondas de juego, los equipos que tienen un desempeño deficiente, que podrían haber sido rápidamente eliminados de la contienda por el título, se ven obligados a jugar sus partidos restantes. Por lo tanto, los partidos se juegan al final de la competencia entre competidores que no tienen ninguna posibilidad restante de éxito. Además, algunos partidos posteriores emparejarán a un competidor que todavía tiene algo por lo que jugar contra otro que no lo tiene. También puede ser posible que un competidor juegue con los oponentes más fuertes en una ronda de todos contra todos en rápida sucesión mientras que otros los juegan intermitentemente con oponentes más débiles. Esta asimetría significa que jugar con los mismos oponentes no es necesariamente completamente equitativo.
Tampoco se programa una final de exhibición a menos que (por coincidencia) dos competidores se enfrenten en el último partido del torneo, y el resultado de ese partido determine el campeonato. Un ejemplo notable de un evento de este tipo fue el partido de la Copa Mundial de la FIFA de 1950 entre Uruguay y Brasil .
Equipos calificados
Surgen más problemas cuando se utiliza un sistema de todos contra todos como ronda clasificatoria dentro de un torneo más grande. Es posible que un competidor que ya se clasificó para la siguiente etapa antes de su último partido no se esfuerce demasiado (para conservar recursos para la siguiente etapa) o incluso pierda deliberadamente (si el oponente programado para la siguiente etapa para un clasificado que se encuentra en una posición inferior se percibe como más fácil que para uno que se encuentra en una posición superior).
Cuatro parejas en el torneo de bádminton femenino de dobles de los Juegos Olímpicos de 2012 , que se habían clasificado para la siguiente ronda, fueron expulsadas de la competición por intentar perder en la fase de todos contra todos para evitar a sus compatriotas y oponentes mejor clasificados. [9] La fase de todos contra todos en los Juegos Olímpicos fue una nueva introducción, y estos problemas potenciales se conocían fácilmente antes del torneo; se realizaron cambios antes de los próximos Juegos Olímpicos para evitar que se repitieran estos eventos.
Círculo de la muerte
Otra desventaja, especialmente en round-robins más pequeños, es el "círculo de la muerte", donde los equipos no pueden separarse en un registro de enfrentamientos directos. En un round-robin de tres equipos, donde A derrota a B, B derrota a C y C derrota a A, los tres competidores tendrán un registro de una victoria y una derrota, y será necesario utilizar un desempate para separar a los equipos. [10] Esto ocurrió durante el Grupo E de la Copa Mundial de la FIFA de 1994 , donde los cuatro equipos terminaron con un registro de una victoria, un empate y una derrota. Este fenómeno es análogo a la paradoja de Condorcet en la teoría de la votación.
Algoritmo de programación
Si es el número de competidores, un torneo de todos contra todos requiere juegos. Si es par, entonces en cada una de las rondas, se pueden jugar juegos simultáneamente, siempre que existan recursos suficientes (por ejemplo, canchas para un torneo de tenis ). Si es impar, habrá rondas, cada una con juegos, y un competidor no tendrá ningún juego en esa ronda.
Método del círculo
El método del círculo es un algoritmo simple para crear un cronograma para un torneo de todos contra todos. A todos los competidores se les asignan números y luego se los empareja en la primera ronda:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 14 | 13 | 12 | 11 | 10 | 9 | 8 |
A continuación, se fija uno de los competidores en la primera o última columna de la tabla (el número uno en este ejemplo) y los demás se rotan una posición en el sentido de las agujas del reloj:
| 1 | 14 | 2 | 3 | 4 | 5 | 6 |
| 13 | 12 | 11 | 10 | 9 | 8 | 7 |
| 1 | 13 | 14 | 2 | 3 | 4 | 5 |
| 12 | 11 | 10 | 9 | 8 | 7 | 6 |
Esto se repite hasta que la siguiente iteración conduzca nuevamente a los emparejamientos iniciales:
| 1 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 14 | 13 | 12 | 11 | 10 | 9 |
Con un número par de competidores, este algoritmo realiza todas las combinaciones posibles de ellos (lo que equivale a que todos los pares realizados sean diferentes).
En primer lugar, el algoritmo obviamente realiza cada par de competidores si uno de ellos es igual (el competidor que no se mueve).
A continuación, para parejas de no competidores, supongamos que su distancia es el número de veces que se debe realizar la rotación para que un competidor llegue a la posición que tenía el otro.
En el ejemplo dado ( ), tiene distancia a y a y tiene distancia a y a .
En una ronda, una posición que no sea la más a la izquierda (sin incluir ) solo puede ser ocupada por competidores de una distancia fija. En la ronda del ejemplo, en la segunda posición juega el competidor contra , su distancia es . En la ronda , esta posición la ocupan los competidores y , que también tienen una distancia , etc. De manera similar, la siguiente posición ( contra en la ronda , contra en la ronda , etc.) solo puede albergar competidores de distancia-.
Para cada , hay exactamente pares de distancias . Hay rondas y todas ellas realizan un par de distancias en la misma posición. Claramente, estos pares son diferentes entre sí. La conclusión es que se realizan todos los pares de distancias.
Esto es válido para cada , por lo tanto, se realiza cada par.
Si hay un número impar de competidores, se puede agregar un competidor ficticio, cuyo oponente programado en una ronda determinada no juega y tiene un bye . Por lo tanto, el cronograma se puede calcular como si el competidor ficticio fuera un jugador común, ya sea fijo o rotativo.
En lugar de rotar una posición, cualquier número primo relativo a generará un calendario completo. Las filas superior e inferior pueden indicar local/visitante en deportes, blancas/negras en ajedrez , etc.; para garantizar la equidad, esto debe alternarse entre rondas ya que el competidor 1 siempre está en la primera fila. Si, por ejemplo, los competidores 3 y 8 no pudieran cumplir con su encuentro en la tercera ronda, sería necesario reprogramarlo fuera de las otras rondas, ya que ambos competidores ya se enfrentarían a otros oponentes en esas rondas. Las restricciones de programación más complejas pueden requerir algoritmos más complejos. [11] Este calendario se aplica en torneos de ajedrez y damas de partidas rápidas, donde los jugadores se mueven físicamente alrededor de una mesa. En Francia, esto se llama sistema Carrusel -Berger (Système Rutch-Berger). [12]
El calendario también se puede utilizar para torneos de todos contra todos "asincrónicos" en los que todos los partidos tienen lugar en momentos diferentes (por ejemplo, porque sólo hay una sede). Los partidos se juegan de izquierda a derecha en cada ronda, y desde la primera ronda hasta la última. Cuando el número de competidores es par, este calendario funciona bien con respecto a las medidas de calidad y equidad, como la cantidad de descanso entre partidos. Por otro lado, cuando el número de competidores es impar, no funciona tan bien y un calendario diferente es superior con respecto a estas medidas. [13]
Mesas Berger
Alternativamente, las tablas de Berger, [14] llamadas así en honor al maestro de ajedrez austríaco Johann Berger , se utilizan ampliamente en la planificación de torneos. [15] Berger publicó las tablas de emparejamiento en sus dos Schach-Jahrbücher (Anales de ajedrez), [16] [17] con la debida referencia a su inventor Richard Schurig. [18] [19]
| Ronda 1 | 1 – 14 | 2 – 13 | 3 – 12 | 4 – 11 | 5 – 10 | 6 – 9 | 7 – 8 |
|---|---|---|---|---|---|---|---|
| Ronda 2 | 14 – 8 | 9 – 7 | 10 – 6 | 11 – 5 | 12 – 4 | 13 – 3 | 1 – 2 |
| Ronda 3 | 2 – 14 | 3 – 1 | 4 – 13 | 5 – 12 | 6 – 11 | 7 – 10 | 8 – 9 |
| ... | ... | ||||||
| Ronda 13 | 7 – 14 | 8 – 6 | 9 – 5 | 10 – 4 | 11 – 3 | 12 – 2 | 13 – 1 |
Esto constituye un programa en el que el jugador 14 tiene una posición fija y todos los demás jugadores rotan posiciones en sentido antihorario. Este programa se genera fácilmente de forma manual. Para construir la siguiente ronda, el último jugador, el número 8 en la primera ronda, se mueve a la cabeza de la mesa, seguido por el jugador 9 contra el jugador 7, el jugador 10 contra el 6, hasta el jugador 1 contra el jugador 2. Aritméticamente, esto equivale a sumar a la fila anterior, con la excepción del jugador . Cuando el resultado de la suma es mayor que , entonces se resta de la suma.
Este programa también se puede representar como una tabla (n-1, n-1), que expresa una ronda en la que los jugadores se enfrentan entre sí. Por ejemplo, el jugador 7 juega contra el jugador 11 en la ronda 4. Si un jugador se enfrenta a sí mismo, esto muestra un bye o un juego contra el jugador n. Todos los juegos en una ronda constituyen una diagonal en la tabla.
|
|
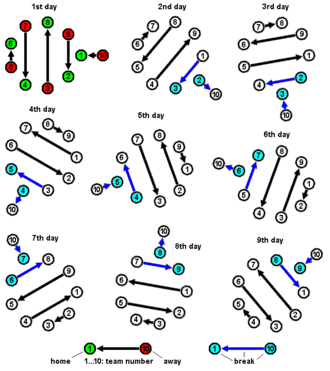
El cronograma anterior también se puede representar mediante un gráfico, como se muestra a continuación:

Tanto el gráfico como la tabla fueron descritos por Édouard Lucas en [20] como un rompecabezas matemático recreativo. Lucas, que describe el método como simple e ingenioso , atribuye la solución a Felix Walecki, un profesor del Lycée Condorcet . Lucas también incluyó una solución alternativa mediante un rompecabezas deslizante .
Mnemotécnico
Para recordar fácilmente este método, se puede utilizar la siguiente regla mnemotécnica. A partir de la primera ronda,
lugar = 1 ╭─────────────────────────────────────── ────────── ───┐1—ω >>> 2—13 >>> 3—12 >>> 4—11 >>> 5—10 >>> 6—9 >>> 7—8
La siguiente ronda se construye:
ω—8 >>> 9—7 >>> 10—6 >>> 11—5 >>> 12—4 >>> 13—3 >>> 1—2
y luego,
2—ω >>> 3—1 >>> 4—13 >>> 5—12 >>> 6—11 >>> 7—10 >>> 8—9ω—9 >>> ...
Si el número de jugadores es impar, el jugador que ocupa el primer lugar obtiene un pase. Si el número es par, un jugador adicional (ω) se convierte en el oponente.
Construcción original de tablas de emparejamiento de Richard Schurig (1886)
Para un número par o impar de competidores, Schurig [19] construye una tabla con filas verticales y filas horizontales. Luego la llena comenzando desde la esquina superior izquierda repitiendo la secuencia de números del 1 al . A continuación, se muestra una tabla de ejemplo para 7 u 8 competidores:
| Ronda 1 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Ronda 2 | 5 | 6 | 7 | 1 |
| Ronda 3 | 2 | 3 | 4 | 5 |
| Ronda 4 | 6 | 7 | 1 | 2 |
| Ronda 5 | 3 | 4 | 5 | 6 |
| Ronda 6 | 7 | 1 | 2 | 3 |
| Ronda 7 | 4 | 5 | 6 | 7 |
Luego, para obtener a los oponentes, se construye una segunda tabla. Cada fila horizontal se llena con los mismos números que la fila de la tabla anterior (la última fila se llena con los números de la primera fila de la tabla original), pero en orden inverso (de derecha a izquierda).
| Ronda 1 | – 1 | – 7 | – 6 | – 5 |
|---|---|---|---|---|
| Ronda 2 | – 5 | – 4 | – 3 | – 2 |
| Ronda 3 | – 2 | – 1 | – 7 | – 6 |
| Ronda 4 | – 6 | – 5 | – 4 | – 3 |
| Ronda 5 | – 3 | – 2 | – 1 | – 7 |
| Ronda 6 | – 7 | – 6 | – 5 | – 4 |
| Ronda 7 | – 4 | – 3 | – 2 | – 1 |
Fusionando las tablas anteriores:
| Ronda 1 | 1 – 1 | 2 – 7 | 3 – 6 | 4 – 5 |
|---|---|---|---|---|
| Ronda 2 | 5 – 5 | 6 – 4 | 7 – 3 | 1 – 2 |
| Ronda 3 | 2 – 2 | 3 – 1 | 4 – 7 | 5 – 6 |
| Ronda 4 | 6 – 6 | 7 – 5 | 1 – 4 | 2 – 3 |
| Ronda 5 | 3 – 3 | 4 – 2 | 5 – 1 | 6 – 7 |
| Ronda 6 | 7 – 7 | 1 – 6 | 2 – 5 | 3 – 4 |
| Ronda 7 | 4 – 4 | 5 – 3 | 6 – 2 | 7 – 1 |
Luego se actualiza la primera columna: si el número de competidores es par, el número de jugador se sustituye alternativamente por la primera y segunda posición, mientras que si el número de competidores es impar se utiliza un bye en su lugar.
Las tablas de emparejamiento se publicaron como anexo a las disposiciones para la celebración de torneos magistrales. Schurig no proporcionó ninguna prueba ni motivación para su algoritmo. [21]
Véase también
- Sistema de clasificación de torneos grupales , incluidos detalles de los sistemas de desempate
- Diseño combinatorio , un diseño de torneo equilibrado de orden n (a BTD( n ))
- Torneo (teoría de grafos) , modelo matemático de un torneo de todos contra todos
- Torneo del sistema McMahon , una variación del sistema suizo que incorpora clasificaciones previas al torneo para evitar emparejamientos desequilibrados al principio
- Sistema de playoffs Shaughnessy , un tipo de torneo de eliminación simple en el que participan cuatro equipos.
- Sistema McIntyre , una serie de formatos de torneos que combinan características de los torneos de eliminación simple y doble
- Movimientos de puente duplicados
- Lista de torneos de ajedrez con formato todos contra todos
- Sistema Scheveningen , donde cada miembro de un equipo juega contra cada miembro del otro.
- El método de Copeland
- Método Condorcet
- Criterio de Condorcet
- Tres puntos por victoria , para las implicaciones de los diferentes sistemas de puntuación en la fase de grupos
Referencias
- ^ ab Webster's Third New International Dictionary of the English Language, Unabridged (1971, G. & C. Merriam Co), pág. 1980.
- ^ Orcutt, William Dana (1895). Boletín oficial de tenis sobre césped. Vol. 2. Nueva York: The Editors. págs. 1, 3.
- ^ Strehlov, Richard A; Wright, Sue Ellen, eds. (1993). Terminología estandarizada para una mejor comunicación: práctica, teoría aplicada y resultados . Vol. 1166. ASTM. págs. 336–337. ISBN. 0-8031-1493-1.
- ^ Diccionario Brewer de frases y fábulas . Nueva York: Harper & Brother Publishers. pág. 786.
- ^ "Glosario de términos utilizados en relación con el billar". Billiard Monthly . Asociación Inglesa de Billar Amateur. Febrero de 1912. Archivado desde el original el 3 de marzo de 2022.
Torneo americano: torneo en el que cada jugador debe enfrentarse por turno a todos los demás jugadores.
- ^ Allied. "Torneo americano". Diccionario Chambers del siglo XXI . Allied Publishers. pág. 38. ISBN 978-0550106254. Recuperado el 1 de agosto de 2012 .
- ^ Mead, Shepherd (1977). Cómo triunfar en el tenis sin esforzarse demasiado: la forma sencilla y práctica de hacer todo lo que ningún profesional del tenis puede enseñarte. McKay. pág. 130. ISBN 9780679507499. Recuperado el 1 de agosto de 2012 .
- ^ "Introducción a los torneos clasificados por la USCF" (PDF) . Federación Estadounidense de Ajedrez . 23 de febrero de 2006. Archivado (PDF) del original el 23 de febrero de 2022.
- ^ "Ocho jugadores olímpicos de bádminton descalificados por 'lanzar juegos'". The Guardian . 1 de agosto de 2012 . Consultado el 1 de agosto de 2012 .
- ^ "UC Berkeley Quiz Bowl: Cómo hacer horarios". www.ocf.berkeley.edu .
- ^ Dinitz, Jeff (13 de noviembre de 2004). "Diseño de calendarios para ligas y torneos" (PDF) . Página de inicio de Jeff Dinitz . Mount Saint Mary College: TEORÍA DE GRAFOS DÍA 48. Archivado (PDF) del original el 23 de febrero de 2022.
- ^ Le livre de l'arbitre: edición 2008 (PDF) (en francés). Fédération Française des Échecs. 2008. pág. 56.ISBN 978-2-915853-01-8. Archivado (PDF) del original el 19 de enero de 2013.
- ^ Suksompong, Warut (2016). "Programación de torneos asincrónicos de todos contra todos". Operations Research Letters . 44 (1): 96–100. arXiv : 1804.04504 . doi :10.1016/j.orl.2015.12.008. S2CID 4931332.
- ^ Tabla de Berger (en francés) , ejemplos de calendarios de todos contra todos con hasta 30 participantes.
- ^ "C. Reglas generales y recomendaciones técnicas para torneos / 05. Reglamento general para competiciones / Reglamento general para competiciones. Anexo 1: Detalles de la tabla Berger /". Manual de la FIDE. FIDE.(página de contenido)
- ^ Berger, Johann (1893). Schach-Jahrbuch für 1892/93 (en alemán). Leipzig. págs. 26-31. OCLC 651254787.
{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace ) - ^ Berger, Johann (1899). Schach-Jahrbuch für 1899/1900: Fortsetzung des Schach-Jahrbuches für 1892/93 (en alemán). Leipzig. págs. 21-27. OCLC 651254792.
{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace ) - ^ Richard Schurig (en francés)
- ^ ab Schurig, Richard (1886). "Die Paarung der Theilnehmer eines Turniers". Deutsche Schachzeitung (en alemán). 41 : 134-137. OCLC 556959107.Deutsche Schachzeitung en la biblioteca digital HathiTrust
- ^ Lucas, Eduardo (1883). "Los juegos de señoritas". Récréations Mathématiques (en francés). París: Gauthier-Villars. págs. 161-197.
- ^ Ahrens, Wilhelm (1901). "XIV Anordnungs Probleme, § 1 Anordnungen im Kreise, Aufgabe 2". Mathematische Unterhaltungen und Spiele (en alemán). Leipzig: BG Teubner. págs. 259–272. arca:/13960/t2w37mv93.
























