Teoría del campo cristalino
En física molecular , la teoría del campo cristalino ( CFT ) describe la ruptura de degeneraciones de estados orbitales de electrones, usualmente orbitales d o f , debido a un campo eléctrico estático producido por una distribución de carga circundante (vecinos aniones). Esta teoría se ha utilizado para describir varias espectroscopias de complejos de coordinación de metales de transición , en particular espectros ópticos (colores). La CFT explica con éxito algunas propiedades magnéticas , colores , entalpías de hidratación y estructuras de espinela de complejos de metales de transición, pero no intenta describir el enlace. La CFT fue desarrollada por los físicos Hans Bethe [1] y John Hasbrouck van Vleck [2] en la década de 1930. Posteriormente, la CFT se combinó con la teoría de orbitales moleculares para formar la teoría del campo de ligandos (LFT) , más realista y compleja , que brinda información sobre el proceso de enlace químico en complejos de metales de transición. La CFT se puede complicar aún más al romper los supuestos hechos sobre las energías orbitales relativas del metal y del ligando, lo que requiere el uso de la teoría del campo de ligando invertido (ILFT) para describir mejor el enlace.
Descripción general
Según la teoría de campos cristalinos, la interacción entre un metal de transición y los ligandos surge de la atracción entre el catión metálico cargado positivamente y la carga negativa de los electrones no enlazantes del ligando. La teoría se desarrolla considerando los cambios de energía de los cinco orbitales d degenerados al estar rodeados por una matriz de cargas puntuales que consisten en los ligandos. A medida que un ligando se acerca al ion metálico, los electrones del ligando estarán más cerca de algunos de los orbitales d y más lejos de otros, lo que provoca una pérdida de degeneración. Los electrones en los orbitales d y los del ligando se repelen entre sí debido a la repulsión entre cargas iguales. Por lo tanto, los electrones d más cercanos a los ligandos tendrán una energía mayor que los más alejados, lo que da como resultado la división de energía de los orbitales d . Esta división se ve afectada por los siguientes factores:
- La naturaleza del ion metálico.
- El estado de oxidación del metal. Un estado de oxidación más alto conduce a una mayor división en relación con el campo esférico.
- la disposición de los ligandos alrededor del ion metálico.
- el número de coordinación del metal (es decir, tetraédrico, octaédrico...)
- La naturaleza de los ligandos que rodean al ion metálico. Cuanto más fuerte sea el efecto de los ligandos, mayor será la diferencia entre los grupos d de alta y baja energía .
El tipo más común de complejo es octaédrico , en el que seis ligandos forman los vértices de un octaedro alrededor del ion metálico. En la simetría octaédrica, los orbitales d se dividen en dos conjuntos con una diferencia de energía, Δ oct (el parámetro de división del campo cristalino , también comúnmente denotado por 10 Dq para diez veces el "diferencial de cuantos" [3] [4] ) donde los orbitales d xy , d xz y d yz tendrán menor energía que los orbitales d z 2 y d x 2 - y 2 , que tendrán mayor energía, porque el primer grupo está más alejado de los ligandos que el segundo y, por lo tanto, experimenta menos repulsión. Los tres orbitales de menor energía se denominan colectivamente t 2g , y los dos orbitales de mayor energía como e g . Estas etiquetas se basan en la teoría de la simetría molecular : son los nombres de las representaciones irreducibles del grupo puntual octaédrico , O h . (ver la tabla de caracteres O h ) Los diagramas de energía orbital típicos se dan a continuación en la sección Alto espín y bajo espín.
Los complejos tetraédricos son el segundo tipo más común; aquí cuatro ligandos forman un tetraedro alrededor del ion metálico. En una división de campo cristalino tetraédrico, los orbitales d se dividen nuevamente en dos grupos, con una diferencia de energía de Δ tet . Los orbitales de menor energía serán d z 2 y d x 2 - y 2 , y los orbitales de mayor energía serán d xy , d xz y d yz - opuesto al caso octaédrico. Además, dado que los electrones del ligando en simetría tetraédrica no están orientados directamente hacia los orbitales d , la división de energía será menor que en el caso octaédrico. Las geometrías planares cuadradas y otras geometrías complejas también se pueden describir mediante CFT.
El tamaño del espacio Δ entre los dos o más conjuntos de orbitales depende de varios factores, incluidos los ligandos y la geometría del complejo. Algunos ligandos siempre producen un valor pequeño de Δ, mientras que otros siempre dan lugar a una gran división. Las razones de esto se pueden explicar mediante la teoría del campo de ligandos . La serie espectroquímica es una lista derivada empíricamente de ligandos ordenados por el tamaño de la división Δ que producen (de Δ pequeño a Δ grande; consulte también esta tabla ):
I − < Br − < S 2− < SCN − (S–enlazado) < Cl − < NO 3 − < N 3 − < F − < OH − < C 2 O 4 2− < H 2 O < NCS − (N–enlazado) < CH 3 CN < py < NH 3 < en < 2,2'-bipiridina < phen < NO 2 − < PPh 3 < CN − < CO .
Es útil observar que los ligandos que producen la mayor división son aquellos que pueden participar en la unión posterior del metal al ligando .
El estado de oxidación del metal también contribuye al tamaño de Δ entre los niveles de energía alta y baja. A medida que aumenta el estado de oxidación para un metal determinado, aumenta la magnitud de Δ. El complejo AV 3+ tendrá un Δ mayor que un complejo V 2+ para un conjunto dado de ligandos, ya que la diferencia en la densidad de carga permite que los ligandos estén más cerca de un ion V 3+ que de un ion V 2+ . La distancia menor entre el ligando y el ion metálico da como resultado un Δ mayor, porque los electrones del ligando y del metal están más cerca entre sí y, por lo tanto, se repelen más.
Alto efecto y bajo efecto

Los ligandos que causan una gran división Δ de los orbitales d se denominan ligandos de campo fuerte, como CN − y CO de la serie espectroquímica . En complejos con estos ligandos, es desfavorable colocar electrones en los orbitales de alta energía. Por lo tanto, los orbitales de menor energía se llenan completamente antes de que comience la población de los conjuntos superiores según el principio de Aufbau . Los complejos como este se denominan "de espín bajo". Por ejemplo, NO 2 − es un ligando de campo fuerte y produce un Δ grande. El ion octaédrico [Fe(NO 2 ) 6 ] 3− , que tiene 5 electrones d , tendría el diagrama de división octaédrica que se muestra a la derecha con los cinco electrones en el nivel t 2 g . Por lo tanto, este estado de espín bajo no sigue la regla de Hund .

Por el contrario, los ligandos (como I − y Br − ) que causan una pequeña división Δ de los orbitales d se denominan ligandos de campo débil. En este caso, es más fácil poner electrones en el conjunto de orbitales de mayor energía que poner dos en el mismo orbital de baja energía, porque dos electrones en el mismo orbital se repelen entre sí. Entonces, se pone un electrón en cada uno de los cinco orbitales d de acuerdo con la regla de Hund, y se forman complejos de "alto espín" antes de que ocurra cualquier apareamiento. Por ejemplo, Br − es un ligando de campo débil y produce un pequeño Δ oct . Entonces, el ion [FeBr 6 ] 3− , nuevamente con cinco electrones d , tendría un diagrama de división octaédrica donde los cinco orbitales están ocupados individualmente.
Para que se produzca una división de espín bajo, el coste energético de colocar un electrón en un orbital ya ocupado individualmente debe ser menor que el coste de colocar el electrón adicional en un orbital e g con un coste energético de Δ. Como se señaló anteriormente, e g se refiere a d z 2 y d x 2 - y 2 que tienen una energía superior a t 2g en los complejos octaédricos. Si la energía necesaria para aparear dos electrones es mayor que Δ, el coste energético de colocar un electrón en un orbital e g , se produce una división de espín alto.
La energía de división del campo cristalino para los complejos metálicos tetraédricos (cuatro ligandos) se denomina Δ tet y es aproximadamente igual a 4/9Δ oct (para el mismo metal y los mismos ligandos). Por lo tanto, la energía necesaria para aparear dos electrones suele ser mayor que la energía necesaria para colocar los electrones en los orbitales de mayor energía. Por lo tanto, los complejos tetraédricos suelen tener un espín alto.
El uso de estos diagramas de desdoblamiento puede ayudar a predecir las propiedades magnéticas de los compuestos de coordinación. Un compuesto que tiene electrones desapareados en su diagrama de desdoblamiento será paramagnético y será atraído por los campos magnéticos, mientras que un compuesto que carece de electrones desapareados en su diagrama de desdoblamiento será diamagnético y será débilmente repelido por un campo magnético.
Energía de estabilización
La energía de estabilización del campo cristalino (CFSE) es la estabilidad que resulta de colocar un ion metálico de transición en el campo cristalino generado por un conjunto de ligandos. Surge debido al hecho de que cuando los orbitales d se dividen en un campo de ligando (como se describió anteriormente), algunos de ellos se vuelven más bajos en energía que antes con respecto a un campo esférico conocido como el baricentro en el que los cinco orbitales d están degenerados. Por ejemplo, en un caso octaédrico, el conjunto t 2g se vuelve más bajo en energía que los orbitales en el baricentro. Como resultado de esto, si hay electrones ocupando estos orbitales, el ion metálico es más estable en el campo de ligando en relación con el baricentro en una cantidad conocida como CFSE. Por el contrario, los orbitales e g (en el caso octaédrico) tienen mayor energía que en el baricentro, por lo que poner electrones en estos reduce la cantidad de CFSE.

Si la división de los orbitales d en un campo octaédrico es Δ oct , los tres orbitales t 2g se estabilizan con respecto al baricentro en 2 / 5 Δ oct , y los orbitales e g se desestabilizan en 3 / 5 Δ oct . Como ejemplos, considere las dos configuraciones d 5 que se muestran más arriba en la página. El ejemplo de espín bajo (arriba) tiene cinco electrones en los orbitales t 2g , por lo que el CFSE total es 5 x 2 / 5 Δ oct = 2Δ oct . En el ejemplo de alto espín (inferior), el CFSE es (3 x 2 / 5 Δ oct ) - (2 x 3 / 5 Δ oct ) = 0 - en este caso, la estabilización generada por los electrones en los orbitales inferiores se cancela por el efecto desestabilizador de los electrones en los orbitales superiores.
Propiedades ópticas
Las propiedades ópticas (detalles de los espectros de absorción y emisión) de muchos complejos de coordinación se pueden explicar mediante la teoría de campos cristalinos. Sin embargo, a menudo los colores más oscuros de los complejos metálicos surgen de excitaciones de transferencia de carga más intensas . [5]
Geometrías y diagramas de división
| Nombre | Forma | Diagrama de energía |
|---|---|---|
| Octaédrico |  | 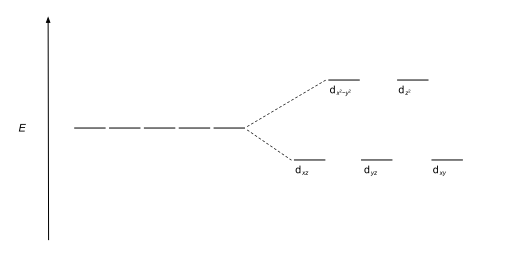 |
| Bipiramidal pentagonal | 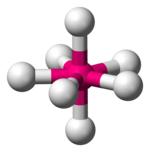 | 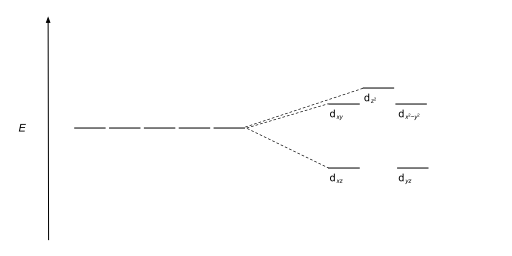 |
| Antiprismático cuadrado | 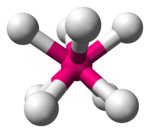 | 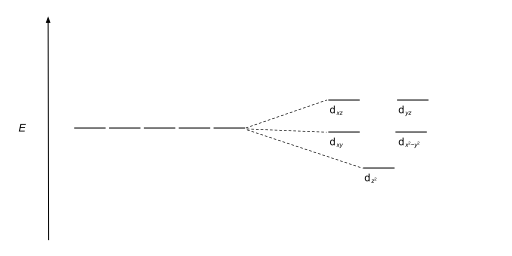 |
| Plano cuadrado |  | 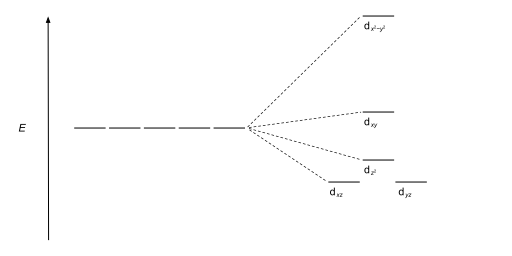 |
| Pirámide cuadrada | 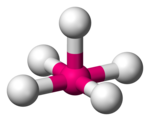 | 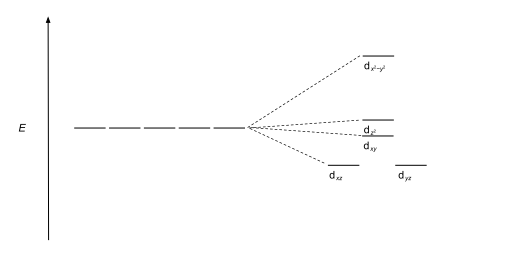 |
| Tetraédrico | 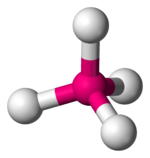 | 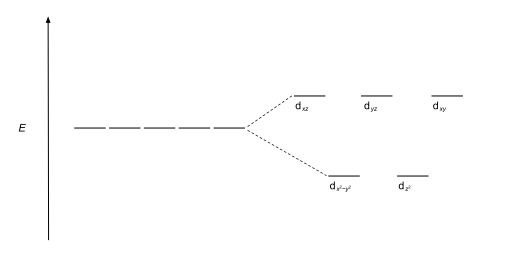 |
| Bipiramidal trigonal |  | 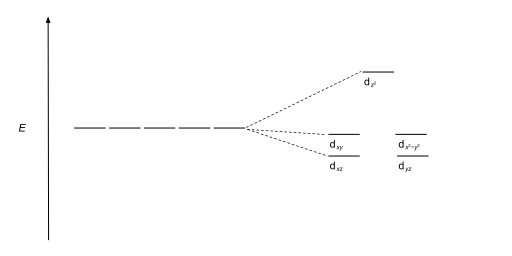 |
Véase también
- Anomalía de Schottky : pico de baja temperatura en la capacidad térmica que se observa en materiales que contienen impurezas magnéticas de alto espín, a menudo debido a la división del campo cristalino
- Teoría del campo de ligandos
- Teoría de orbitales moleculares
Referencias
- ^ Bethe, H. (1929). "Termaufspaltung en Kristallen". Annalen der Physik (en alemán). 395 (2): 133–208. Código bibliográfico : 1929AnP...395..133B. doi : 10.1002/andp.19293950202. ISSN 1521-3889.
- ^ Van Vleck, J. (1932). "Teoría de las variaciones en la anisotropía paramagnética entre diferentes sales del grupo del hierro". Physical Review . 41 (2): 208–215. Bibcode :1932PhRv...41..208V. doi :10.1103/PhysRev.41.208.
- ^ Penney, William G.; Schlapp, Robert (1932). "La influencia de los campos cristalinos en las susceptibilidades de las sales de iones paramagnéticos. I. Las tierras raras, especialmente Pr y Nd". Physical Review . 41 (2): 194–207. Bibcode :1932PhRv...41..194P. doi :10.1103/PhysRev.41.194. ISSN 0031-899X.
- ^ Schlapp, Robert; Penney, William G. (1932). "Influencia de los campos cristalinos en las susceptibilidades de las sales de iones paramagnéticos. II. El grupo del hierro, especialmente Ni, Cr y Co". Physical Review . 42 (5): 666–686. Bibcode :1932PhRv...42..666S. doi :10.1103/PhysRev.42.666. ISSN 0031-899X.\
- ^ GL Miessler y DA Tarr “Química inorgánica” 2.ª ed. (Prentice Hall 1999), pág. 379 ISBN 0-13-841891-8 .
Lectura adicional
- Housecroft, CE; Sharpe, AG (2004). Química inorgánica (2.ª ed.). Prentice Hall. ISBN 978-0-13-039913-7.
- Miessler, GL; Tarr, DA (2003). Química inorgánica (3.ª ed.). Pearson Prentice Hall. ISBN 978-0-13-035471-6.
- Orgel, Leslie E. (1960). Introducción a la química de los metales de transición: teoría del campo de ligando . Methuen. ISBN 978-0416634402.
- Shriver, DF; Atkins, PW (2001). Química inorgánica (4.ª ed.). Oxford University Press. págs. 227–236. ISBN 978-0-8412-3849-7.
- Silberberg, Martin S (2006). Química: la naturaleza molecular de la materia y el cambio (4.ª ed.). Nueva York: McGraw Hill Company. pp. 1028–1034. ISBN 978-0-8151-8505-5.
- Zumdahl, Steven S (2005). Principios químicos (5.ª ed.). Houghton Mifflin Company. págs. 550-551, 957-964. ISBN 978-0-669-39321-7.
Enlaces externos
- Teoría de campos cristalinos, método de enlace fuerte y efecto Jahn-Teller en E. Pavarini, E. Koch, F. Anders y M. Jarrell (eds.): Electrones correlacionados: de modelos a materiales, Jülich 2012, ISBN 978-3-89336-796-2