Ecuación sextica

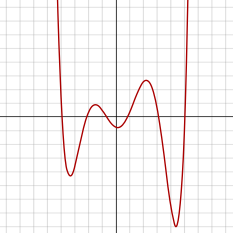
En álgebra , un polinomio séxtico (o hexico ) es un polinomio de grado seis. Una ecuación séxtica es una ecuación polinómica de grado seis, es decir, una ecuación cuyo lado izquierdo es un polinomio séxtico y cuyo lado derecho es cero. Más precisamente, tiene la forma:

${\displaystyle ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g=0,\,}$

donde a ≠ 0 y los coeficientes a , b , c , d , e , f , g pueden ser números enteros , números racionales , números reales , números complejos o, más generalmente, miembros de cualquier cuerpo .

Una función séxtica es una función definida por un polinomio séxtico. Debido a que tienen un grado par, las funciones séxticas parecen similares a las funciones cuárticas cuando se grafican, excepto que pueden poseer un máximo local y un mínimo local adicionales cada una. La derivada de una función séxtica es una función quíntica .

Como una función séxtica se define mediante un polinomio de grado par, tiene el mismo límite infinito cuando el argumento tiende a infinito positivo o negativo . Si el coeficiente principal a es positivo, entonces la función crece hasta infinito positivo en ambos lados y, por lo tanto, la función tiene un mínimo global. Del mismo modo, si a es negativo, la función séxtica decrece hasta infinito negativo y tiene un máximo global.

Algunas ecuaciones de sexto grado, como ax ⁶ + dx ³ + g = 0 , se pueden resolver factorizándolas en radicales, pero otras ecuaciones sextantes no. Évariste Galois desarrolló técnicas para determinar si una ecuación dada se podía resolver mediante radicales, lo que dio origen al campo de la teoría de Galois . ^[1]

De la teoría de Galois se desprende que una ecuación séxtica es resoluble en términos de radicales si y sólo si su grupo de Galois está contenido en el grupo de orden 48 que estabiliza una partición del conjunto de las raíces en tres subconjuntos de dos raíces o en el grupo de orden 72 que estabiliza una partición del conjunto de las raíces en dos subconjuntos de tres raíces.

Existen fórmulas para probar cada caso y, si la ecuación tiene solución, calcular las raíces en términos de radicales. ^[2]

La ecuación séxtica general se puede resolver mediante la función Kampé de Fériet de dos variables . ^[1] Una clase más restringida de séxticas se puede resolver mediante la función hipergeométrica generalizada de una variable utilizando el enfoque de Felix Klein para resolver la ecuación quíntica . ^[1]

La curva de Watt , que surgió en el contexto de los primeros trabajos sobre la máquina de vapor , es una séxtica en dos variables.

Un método para resolver la ecuación cúbica implica transformar variables para obtener una ecuación séxtica que tenga solo términos de grados 6, 3 y 0, que puede resolverse como una ecuación cuadrática en el cubo de la variable.

El adjetivo "sextico" proviene de la raíz latina que significa 6 o 6.º ("sex-t-") y del sufijo griego que significa "perteneciente a" ("-ic"). El adjetivo "hexico", mucho menos común, utiliza el griego tanto para su raíz ( hex- 6) como para su sufijo ( -ik- ). En ambos casos, el prefijo se refiere al grado de la función. A menudo, este tipo de funciones se denominan simplemente "funciones de 6.º grado".

• El sextic de Cayley
• Función cúbica
• Ecuación séptica