Secuencia de Farey

En matemáticas , la sucesión de Farey de orden n es la sucesión de fracciones completamente reducidas , ya sea entre 0 y 1, o sin esta restricción, ^[a] que cuando están en términos más bajos tienen denominadores menores o iguales a n , dispuestas en orden de tamaño creciente.

Con la definición restringida, cada secuencia de Farey comienza con el valor 0, denotado por la fracción ⁠0/1⁠ , y termina con el valor 1, denotado por la fracción ⁠1/1⁠ (aunque algunos autores omiten estos términos).

A una secuencia de Farey a veces se la denomina serie de Farey , lo que no es estrictamente correcto, porque los términos no se suman. ^[2]

Las secuencias de Farey de órdenes 1 a 8 son:

F ₁ = { ⁠0/1⁠ _, ⁠1/1⁠ }

F ₂ = { ⁠0/1⁠ _, ⁠1/2⁠ _, ⁠1/1⁠ }

F3 = { _⁠0/1⁠ _, ⁠1/3⁠ _, ⁠1/2⁠ _, ⁠2/3⁠ _, ⁠1/1⁠ }

F ₄ = { ⁠0/1⁠ _, ⁠1/4⁠ _, ⁠1/3⁠ _, ⁠1/2⁠ _, ⁠2/3⁠ _, ⁠3/4⁠ _, ⁠1/1⁠ }

F ₅ = { ⁠0/1⁠ _, ⁠1/5⁠ _, ⁠1/4⁠ _, ⁠1/3⁠ _, ⁠2/5⁠ _, ⁠1/2⁠ _, ⁠3/5⁠ _, ⁠2/3⁠ _, ⁠3/4⁠ _, ⁠4/5⁠ _, ⁠1/1⁠ }

F6 = { _⁠0/1⁠ _, ⁠1/6⁠ _, ⁠1/5⁠ _, ⁠1/4⁠ _, ⁠1/3⁠ _, ⁠2/5⁠ _, ⁠1/2⁠ _, ⁠3/5⁠ _, ⁠2/3⁠ _, ⁠3/4⁠ _, ⁠4/5⁠ _, ⁠5/6⁠ _, ⁠1/1⁠ }

F7 ₌ { ⁠0/1⁠ _, ⁠1/7⁠ _, ⁠1/6⁠ _, ⁠1/5⁠ _, ⁠1/4⁠ _, ⁠2/7⁠ _, ⁠1/3⁠ _, ⁠2/5⁠ _, ⁠3/7⁠ _, ⁠1/2⁠ _, ⁠4/7⁠ _, ⁠3/5⁠ _, ⁠2/3⁠ _, ⁠5/7⁠ _, ⁠3/4⁠ _, ⁠4/5⁠ _, ⁠5/6⁠ _, ⁠6/7⁠ _, ⁠1/1⁠ }

F8 = { _⁠0/1⁠ _, ⁠1/8⁠ _, ⁠1/7⁠ _, ⁠1/6⁠ _, ⁠1/5⁠ _, ⁠1/4⁠ _, ⁠2/7⁠ _, ⁠1/3⁠ _, ⁠3/8⁠ _, ⁠2/5⁠ _, ⁠3/7⁠ _, ⁠1/2⁠ _, ⁠4/7⁠ _, ⁠3/5⁠ _, ⁠5/8⁠ _, ⁠2/3⁠ _, ⁠5/7⁠ _, ⁠3/4⁠ _, ⁠4/5⁠ _, ⁠5/6⁠ _, ⁠6/7⁠ _, ⁠7/8⁠ _, ⁠1/1⁠ }

F1 = {0/1, 1/1} F2 = {0/1, 1/2, 1/1} F3 = {0/1, 1/3, 1/2, 2/3, 1/1} F4 = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1} F5 = {0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1} F6 = {0/1, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 1/1} F7 = {0/1, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 2/5, 3/7, 1/2, 4/7, 3/5, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 1/1} F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

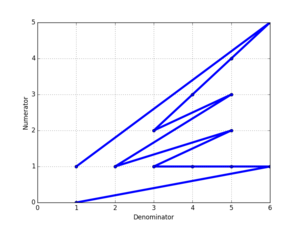
Al representar gráficamente los numeradores frente a los denominadores de una secuencia de Farey se obtiene una forma como la de la derecha, que se muestra para F ₆ .

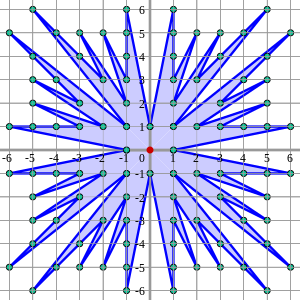
Al reflejar esta forma alrededor de los ejes diagonal y principal se genera el rayo de sol de Farey , que se muestra a continuación. El rayo de sol de Farey de orden n conecta los puntos de la cuadrícula de números enteros visibles desde el origen en el cuadrado de lado 2 n , centrado en el origen. Utilizando el teorema de Pick , el área del rayo de sol es 4(| F _n | − 1) , donde | F _n | es el número de fracciones en Fn.

La historia de la 'serie Farey' es muy curiosa — Hardy & Wright (1979) ^[3]

... una vez más, el hombre cuyo nombre se dio a una relación matemática no fue el descubridor original hasta donde llegan los registros. — Beiler (1964) ^[4]

Las sucesiones de Farey reciben su nombre del geólogo británico John Farey, Sr. , cuya carta sobre estas sucesiones fue publicada en la revista Philosophical Magazine en 1816. Farey conjeturó, sin ofrecer pruebas, que cada nuevo término en una expansión de la sucesión de Farey es el mediante de sus vecinos. La carta de Farey fue leída por Cauchy , quien proporcionó una prueba en sus Exercices de mathématique , y atribuyó este resultado a Farey. De hecho, otro matemático, Charles Haros , había publicado resultados similares en 1802 que no eran conocidos ni por Farey ni por Cauchy. ^[4] Por lo tanto, fue un accidente histórico lo que vinculó el nombre de Farey con estas sucesiones. Este es un ejemplo de la ley de epónimo de Stigler .

La sucesión de Farey de orden n contiene todos los miembros de las sucesiones de Farey de órdenes inferiores. En particular, F _n contiene todos los miembros de F _{n −1} y también contiene una fracción adicional por cada número que sea menor que n y coprimo con n . Por lo tanto, F ₆ consta de F ₅ junto con las fracciones ⁠1/6⁠ y ⁠5/6⁠ .

El término medio de una secuencia de Farey F _n es siempre ⁠1/2⁠ , para n > 1. A partir de esto, podemos relacionar las longitudes de F _n y F _{n −1} utilizando la función totiente de Euler  :${\displaystyle \varphi (n)}$

${\displaystyle |F_{n}|=|F_{n-1}|+\varphi (n).}$

Utilizando el hecho de que | F ₁ | = 2, podemos derivar una expresión para la longitud de F _n : ^[5]

${\displaystyle |F_{n}|=1+\sum _ {m=1}^{n}\varphi (m)=1+\Phi (n),}$

¿Dónde está el totient sumatorio ?${\displaystyle \Phi (n)}$

También contamos con:

${\displaystyle |F_{n}|={\frac {1}{2}}\left(3+\sum _{d=1}^{n}\mu (d)\left\lfloor {\tfrac {n}{d}}\right\rfloor ^{2}\right),}$

y por una fórmula de inversión de Möbius  :

${\displaystyle |F_{n}|={\frac {1}{2}}(n+3)n-\sum _{d=2}^{n}|F_{\lfloor n/d\rfloor }|,}$

donde μ( d ) es la función de Möbius de teoría de números , y es la función de suelo .${\displaystyle \lfloor {\tfrac {n}{d}}\rfloor }$

El comportamiento asintótico de | F _n | es:

${\displaystyle |F_{n}|\sim {\frac {3n^{2}}{\pi ^{2}}}.}$

El número de fracciones de Farey con denominadores iguales a en F _n se da cuando y cero en caso contrario. Con respecto a los numeradores, se puede definir la función que devuelve el número de fracciones de Farey con numeradores iguales a en F _n . Esta función tiene algunas propiedades interesantes como ^[6]${\estilo de visualización k}$${\displaystyle \varphi(k)}$${\displaystyle k\leq n}$${\displaystyle {\mathcal {N}}_{n}(h)}$${\estilo de visualización h}$

${\displaystyle {\mathcal {N}}_{n}(1)=n}$,

${\displaystyle {\mathcal {N}}_{n}(p^{m})=\left\lceil (np^{m})\left(1-1/p\right)\right\rceil }$para cualquier número primo ,${\estilo de visualización p}$

${\displaystyle {\mathcal {N}}_{n+mh}(h)={\mathcal {N}}_{n}(h)+m\varphi (h)}$ para cualquier entero ,${\displaystyle m\geq 0}$

${\displaystyle {\mathcal {N}}_{n}(4h)={\mathcal {N}}_{n}(2h)-\varphi (2h)}$.

En particular, la propiedad de la tercera línea anterior implica y, además, . Esto último significa que, para sucesiones de Farey de orden par n , el número de fracciones con numeradores iguales a n/2 es el mismo que el número de fracciones con denominadores iguales a n/2 , es decir . ${\displaystyle {\mathcal {N}}_{mh}(h)=(m-1)\varphi (h)}$${\displaystyle {\mathcal {N}}_{2h}(h)=\varphi (h)}$${\displaystyle {\mathcal {N}}_{n}(n/2)=\varphi (n/2)}$

El índice de una fracción en la sucesión de Farey es simplemente la posición que ocupa en la sucesión. Esto es de especial relevancia ya que se utiliza en una formulación alternativa de la hipótesis de Riemann , véase más adelante. A continuación se presentan varias propiedades útiles:${\displaystyle I_{n}(a_{k,n})=k}$$Estilo de visualización a_{k,n}$${\displaystyle F_{n}=\{a_{k,n}:k=0,1,\ldots ,m_{n}\}}$$Estilo de visualización a_{k,n}$

${\displaystyle I_{n}(0/1)=0,}$

${\displaystyle I_{n}(1/n)=1,}$

${\displaystyle I_{n}(1/2)=(|F_{n}|-1)/2,}$

${\displaystyle I_{n}(1/1)=|F_{n}|-1,}$

${\displaystyle I_{n}(h/k)=|F_{n}|-1-I_{n}((kh)/k).}$

El índice de donde y es el mínimo común múltiplo de los primeros números, , viene dado por: ^[7]${\estilo de visualización 1/k}$${\displaystyle n/(i+1)<k\leq n/i}$${\estilo de visualización n}$${\estilo de visualización i}$${\displaystyle n={\rm {mcm}}([2,i])}$

${\displaystyle I_{n}(1/k)=1+n\sum _{j=1}^{i}{\frac {\varphi (j)}{j}}-k\Phi (i). }$

Las fracciones que son términos vecinos en cualquier secuencia de Farey se conocen como par de Farey y tienen las siguientes propiedades.

Si ⁠a/b⁠ y ⁠do/d⁠ son vecinos en una secuencia de Farey, con ⁠a/b⁠ < ⁠do/d⁠ , entonces su diferencia ⁠do/d⁠ − ⁠a/b⁠ es igual a ⁠1/bd⁠ . Desde entonces

${\displaystyle {\frac {c}{d}}-{\frac {a}{b}}={\frac {bc-ad}{bd}},}$

Esto equivale a decir que

${\displaystyle bc-ad=1}$.

Así que ⁠1/3⁠ y ⁠2/5⁠ son vecinos en F ₅ , y su diferencia es ⁠1/15⁠ .

Lo inverso también es cierto. Si

${\displaystyle bc-ad=1}$

para números enteros positivos a , b , c y d con a < b y c < d entoncesa/b⁠ y ⁠do/d⁠ serán vecinos en la secuencia de Farey de orden max( b,d ).

Si ⁠pag/q⁠ tiene vecinos ⁠a/b⁠ y ⁠do/d⁠ en alguna secuencia de Farey, con

${\displaystyle {\frac {a}{b}}<{\frac {p}{q}}<{\frac {c}{d}}}$

entonces​pag/q⁠ es el mediante de ⁠a/b⁠ y ⁠do/d⁠ – en otras palabras,

${\displaystyle {\frac {p}{q}}={\frac {a+c}{b+d}}.}$

Esto se deduce fácilmente de la propiedad anterior, ya que si bp – aq = qc – pd = 1 , entonces bp + pd = qc + aq , p ( b + d ) = q ( a + c ) ,pag/q⁠ = ⁠a + c/b + d⁠ .

De ello se deduce que sia/b⁠ y ⁠do/dson vecinos en una secuencia de Farey, entonces el primer término que aparece entre ellos a medida que se incrementa el orden de la secuencia de Farey es

${\displaystyle {\frac {a+c}{b+d}},}$

que aparece por primera vez en la secuencia de Farey de orden b + d .

Así, el primer término que aparece entre ⁠1/3⁠ y ⁠2/5⁠ es ⁠3/8⁠ , que aparece en F ₈ .

El número total de pares de vecinos de Farey en F _n es 2| F _n | − 3.

El árbol de Stern-Brocot es una estructura de datos que muestra cómo se construye la secuencia a partir de 0 ( = ⁠0/1⁠ ) ​​y 1 ( = ⁠1/1⁠ ) ​​, tomando mediantes sucesivos.

Cada par consecutivo de racionales de Farey tiene un área equivalente de 1. ^[8] Véalo interpretando los racionales consecutivos r ₁ = p / q y r ₂ = p ′/ q ′ como vectores ( p , q ) en el plano x–y. El área de A ( p / q , p ′/ q ′) está dada por qp ′ − q ′ p . Como cualquier fracción añadida entre dos fracciones consecutivas previas de la secuencia de Farey se calcula como el mediante (⊕), entonces A ( r ₁ , r ₁ ⊕ r ₂ ) = A ( r ₁ , r ₁ ) + A ( r ₁ , r ₂ ) = A ( r ₁ , r ₂ ) = 1 (ya que r ₁ = 1/0 y r ₂ = 0/1, su área debe ser 1).

Las fracciones que aparecen como vecinas en una sucesión de Farey tienen expansiones de fracciones continuas estrechamente relacionadas . Cada fracción tiene dos expansiones de fracciones continuas: en una, el término final es 1; en la otra, el término final es mayor en 1. Si ⁠pag/q⁠ , que aparece por primera vez en la secuencia de Farey F _q , tiene expansiones fraccionarias continuas

[0; a ₁ , a ₂ , ..., a _{n − 1} , a _n , 1]

[0; a ₁ , a ₂ , ..., a _{n − 1} , a _n + 1]

entonces el vecino más cercano de ⁠pag/q⁠ en F _q (que será su vecino con el denominador más grande) tiene una expansión de fracción continua

[0; a ₁ , a ₂ , ..., a _n ]

y su otro vecino tiene una expansión de fracción continua

[0; a ₁ , a ₂ , ..., a _{n − 1} ]

Por ejemplo, ⁠3/8⁠ tiene las dos expansiones de fracciones continuas [0; 2, 1, 1, 1] y [0; 2, 1, 2] , y sus vecinos en F ₈ son ⁠2/5⁠ , que puede expandirse como [0; 2, 1, 1] ; y ⁠1/3⁠ , que puede expandirse como [0; 2, 1] .

El mcm se puede expresar como el producto de fracciones de Farey como

${\displaystyle {\text{mcm}}[1,2,...,N]=e^{\psi (N)}={\frac {1}{2}}\left(\prod _{r\in F_{N},0<r\leq 1/2}2\sin(\pi r)\right)^{2}}$

donde es la segunda función de Chebyshev . ^{[9] [10]}${\displaystyle \psi(N)}$

Dado que la función totiente de Euler está directamente relacionada con el mcd, también lo está el número de elementos en F _n ,

${\displaystyle |F_{n}|=1+\suma _{m=1}^{n}\varphi (m)=1+\suma \límites _{m=1}^{n}\suma \límites _{k=1}^{m}\mcd(k,m)\cos {2\pi {\frac {k}{m}}}.}$

Para 3 fracciones de Farey cualesquieraa/b⁠ , ⁠do/d⁠ y ⁠mi/F⁠ Se cumple la siguiente identidad entre los mcd de los determinantes de la matriz 2x2 en valor absoluto: ^[11]

${\displaystyle \gcd \left({\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}a&e\\b&f\end{Vmatrix}}\right)=\gcd \left( {\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)=\gcd \left({\begin{Vmatrix}a&e\ \b&f\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)}$

^[7]

Las secuencias de Farey son muy útiles para encontrar aproximaciones racionales de números irracionales. ^[12] Por ejemplo, la construcción por Eliahou ^[13] de un límite inferior en la longitud de ciclos no triviales en el proceso 3 x +1 utiliza secuencias de Farey para calcular una expansión de fracción continua del número log ₂ (3).

En sistemas físicos con fenómenos de resonancia, las secuencias de Farey proporcionan un método muy elegante y eficiente para calcular ubicaciones de resonancia en 1D ^[14] y 2D. ^[15]

Las secuencias de Farey son prominentes en los estudios de planificación de rutas de cualquier ángulo en cuadrículas de celdas cuadradas, por ejemplo, en la caracterización de su complejidad computacional ^[16] u optimalidad. ^[17] La ​​conexión puede considerarse en términos de rutas r -restringidas, es decir, rutas formadas por segmentos de línea que atraviesan como máximo filas y como máximo columnas de celdas. Sea el conjunto de vectores tales que , , y , son coprimos. Sea el resultado de reflejar en la línea . Sea . Entonces, cualquier ruta r -restringida puede describirse como una secuencia de vectores desde . Hay una biyección entre y la secuencia de Farey de orden dada por el mapeo a .${\estilo de visualización r}$${\estilo de visualización r}$${\estilo de visualización Q}$${\estilo de visualización (q,p)}$${\displaystyle 1\leq q\leq r}$${\displaystyle 0\leq p\leq q}$${\displaystyle p}$${\displaystyle q}$${\displaystyle Q*}$${\displaystyle Q}$${\displaystyle y=x}$${\displaystyle S=\{(\pm x,\pm y):(x,y)\in Q\cup Q*\}}$${\displaystyle S}$${\displaystyle Q}$${\displaystyle r}$${\displaystyle (q,p)}$${\displaystyle {\tfrac {p}{q}}}$

Existe una conexión entre la secuencia de Farey y los círculos de Ford .

Por cada fracciónpag/q⁠ (en sus términos más bajos) hay un círculo de Ford C[ ⁠pag/q⁠ ], que es el círculo con radio 1/(2 q ² ) y centro en ( ⁠pag/q⁠ , ⁠1/ 2 q ² ⁠ ). Dos círculos de Ford para fracciones diferentes son disjuntos o son tangentes entre sí: dos círculos de Ford nunca se intersecan. Si 0 < ⁠pag/q⁠ < 1 entonces los círculos de Ford que son tangentes a C[ ⁠pag/q] son ​​precisamente los círculos de Ford para fracciones que son vecinas de ⁠pag/q⁠ en alguna secuencia de Farey.

Así C [ ⁠2/5⁠ ] es tangente a C [ ⁠1/2⁠ ], C [ ⁠1/3⁠ ], C [ ⁠3/7⁠ ], C [ ⁠3/8] , etc.

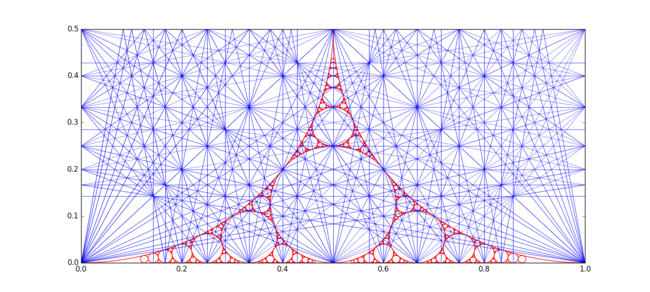
Los círculos de Ford también aparecen en la junta apolínea (0,0,1,1). La siguiente imagen ilustra esto junto con las líneas de resonancia de Farey. ^[18]

Las secuencias de Farey se utilizan en dos formulaciones equivalentes de la hipótesis de Riemann . Supóngase que los términos de son . Defina , en otras palabras, es la diferencia entre el k -ésimo término de la n -ésima secuencia de Farey y el k -ésimo miembro de un conjunto del mismo número de puntos, distribuidos uniformemente en el intervalo unitario. En 1924, Jérôme Franel ^[19] demostró que el enunciado${\displaystyle F_{n}}$${\displaystyle \{a_{k,n}:k=0,1,\ldots ,m_{n}\}}$${\displaystyle d_{k,n}=a_{k,n}-k/m_{n}}$${\displaystyle d_{k,n}}$

${\displaystyle \sum _{k=1}^{m_{n}}d_{k,n}^{2}=O(n^{r})\quad \forall r>-1}$

es equivalente a la hipótesis de Riemann, y luego Edmund Landau ^[20] comentó (justo después del artículo de Franel) que la afirmación

${\displaystyle \sum _{k=1}^{m_{n}}|d_{k,n}|=O(n^{r})\quad \forall r>1/2}$

También es equivalente a la hipótesis de Riemann.

La suma de todas las fracciones de Farey de orden n es la mitad del número de elementos:

${\displaystyle \sum _{r\in F_{n}}r={\frac {1}{2}}|F_{n}|.}$

La suma de los denominadores en la secuencia de Farey es el doble de la suma de los numeradores y se relaciona con la función totiente de Euler:

${\displaystyle \sum _{a/b\in F_{n}}b=2\sum _{a/b\in F_{n}}a=1+\sum _{i=1}^{n}i\varphi (i),}$

que fue conjeturada por Harold L. Aaron en 1962 y demostrada por Jean A. Blake en 1966. ^[21] Una prueba de una línea de la conjetura de Harold L. Aaron es la siguiente. La suma de los numeradores es . La suma de los denominadores es . El cociente de la primera suma por la segunda suma es .${\displaystyle {\displaystyle 1+\sum _{2\leq b\leq n}\sum _{(a,b)=1}a=1+\sum _{2\leq b\leq n}b{\frac {\varphi (b)}{2}}}}$${\displaystyle {\displaystyle 2+\sum _{2\leq b\leq n}\sum _{(a,b)=1}b=2+\sum _{2\leq b\leq n}b\varphi (b)}}$${\displaystyle {\frac {1}{2}}}$

Sean b _j los denominadores ordenados de F _n , entonces: ^[22]

${\displaystyle \sum _{j=0}^{|F_{n}|-1}{\frac {b_{j}}{b_{j+1}}}={\frac {3|F_{n}|-4}{2}}}$

y

${\displaystyle \sum _{j=0}^{|F_{n}|-1}{\frac {1}{b_{j+1}b_{j}}}=1.}$

Sea a _j / b _j la j -ésima fracción de Farey en F _n , entonces

${\displaystyle \sum _{j=1}^{|F_{n}|-1}(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=\sum _{j=1}^{|F_{n}|-1}{\begin{Vmatrix}a_{j-1}&a_{j+1}\\b_{j-1}&b_{j+1}\end{Vmatrix}}=3(|F_{n}|-1)-2n-1,}$

lo cual se demuestra en ^[23] También según esta referencia el término dentro de la suma se puede expresar de muchas maneras diferentes:

${\displaystyle a_{j-1}b_{j+1}-a_{j+1}b_{j-1}={\frac {b_{j-1}+b_{j+1}}{b_{j}}}={\frac {a_{j-1}+a_{j+1}}{a_{j}}}=\left\lfloor {\frac {n+b_{j-1}}{b_{j}}}\right\rfloor ,}$

obteniendo así muchas sumas diferentes sobre los elementos de Farey con el mismo resultado. Utilizando la simetría alrededor de 1/2 la suma anterior puede limitarse a la mitad de la secuencia como

${\displaystyle \sum _{j=1}^{\lfloor |F_{n}|/2\rfloor }(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=3(|F_{n}|-1)/2-n-\lceil n/2\rceil ,}$

La función de Mertens se puede expresar como una suma sobre fracciones de Farey como

${\displaystyle M(n)=-1+\sum _{a\in {\mathcal {F}}_{n}}e^{2\pi ia}}$   donde     es la secuencia de Farey de orden n .${\displaystyle {\mathcal {F}}_{n}}$

Esta fórmula se utiliza en la prueba del teorema de Franel-Landau. ^[24]

Existe un algoritmo sorprendentemente simple para generar los términos de F _n en orden tradicional (ascendente) o en orden no tradicional (descendente). El algoritmo calcula cada entrada sucesiva en términos de las dos entradas anteriores utilizando la propiedad mediante dada anteriormente. Si ⁠a/b⁠ y ⁠do/d⁠ son las dos entradas dadas, y ⁠pag/q⁠ es la siguiente entrada desconocida, entonces ⁠do/d⁠ = ⁠a + p/b + q⁠ . Desde ⁠do/d⁠ está en términos mínimos, debe haber un entero k tal que kc = a + p y kd = b + q , dando p = kc − a y q = kd − b . Si consideramos que p y q son funciones de k , entonces

${\displaystyle {\frac {p(k)}{q(k)}}-{\frac {c}{d}}={\frac {cb-da}{d(kd-b)}}}$

Entonces, cuanto mayor sea k , más cerca estápag/q⁠ llega a ⁠do/d⁠ .

Para obtener el siguiente término en la secuencia , k debe ser lo más grande posible, sujeto a kd − b ≤ n (ya que solo estamos considerando números con denominadores no mayores que n ), por lo que k es el mayor entero ≤ ⁠n + b/d⁠ . Poniendo este valor de k nuevamente en las ecuaciones para p y q se obtiene

${\displaystyle p=\left\lfloor {\frac {n+b}{d}}\right\rfloor c-a}$

${\displaystyle q=\left\lfloor {\frac {n+b}{d}}\right\rfloor d-b}$

Esto se implementa en Python de la siguiente manera:

de  fracciones  importar  Fracción de  colecciones.abc  importar  Generadordef  farey_sequence ( n :  int ,  descending :  bool  =  False )  ->  Generador [ Fracción ]: """  Imprime la n-ésima secuencia de Farey. Permite orden ascendente o descendente.  >>> print(*farey_sequence(5), sep=' ')  0 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 1  """  a ,  b ,  c ,  d  =  0 ,  1 ,  1 ,  n  si es  descendente :  a ,  c  =  1 ,  n  -  1  produce  Fracción ( a ,  b )  mientras  0  <=  c  <=  n :  k  =  ( n  +  b )  //  d  a ,  b ,  c ,  d  =  c ,  d ,  k  *  c  -  a ,  k  *  d  -  b  produce  Fracción ( a ,  b )si  __name__  ==  "__main__" :  importar  doctest doctest .testmod ( )

Las búsquedas de fuerza bruta para encontrar soluciones a ecuaciones diofánticas en números racionales a menudo pueden aprovechar la serie de Farey (para buscar solo formas reducidas). Si bien este código utiliza los dos primeros términos de la secuencia para inicializar a , b , c y d , se podría sustituir cualquier par de términos adyacentes para excluir aquellos que sean menores (o mayores) a un umbral particular. ^[25]

• Patrón ABACABA
• Árbol de Stern-Brocot
• Función totiente de Euler

• Hatcher, Allen (2022), Topología de números , Providence, RI: American Mathematical Society , ISBN 978-1470456115
• Graham, Ronald L. ; Knuth, Donald E. ; Patashnik, Oren (1989). Matemáticas concretas: una base para la informática (2.ª ed.). Boston, MA: Addison-Wesley. págs. 115-123, 133-139, 150, 462-463, 523-524. ISBN 0-201-55802-5.— en particular, véase §4.5 (págs. 115–123), Problema adicional 4.61 (págs. 150, 523–524), §4.9 (págs. 133–139), §9.3, Problema 9.3.6 (págs. 462–463).
• Vepstas, Linas. "El signo de interrogación de Minkowski, GL(2,Z) y el grupo modular" (PDF) .— revisa los isomorfismos del árbol de Stern-Brocot.
• Vepstas, Linas. "Simetrías de mapas de duplicación de períodos" (PDF) .— revisa las conexiones entre las fracciones de Farey y los fractales.
• Cobeli, Cristian; Zaharescu, Alexandru (2003). "La secuencia Haros-Farey a doscientos años. Un estudio". Acta Univ. Apulensis Math. Inform. (5): 1–38. "págs. 1 a 20" (PDF) . Acta Univ. Apulensis . "págs. 21 a 38" (PDF) . Acta Univ. Apulensis .
• Matveev, Andrey O. (2017). Farey Sequences: Duality and Maps Between Subsequences [Secuencias de Farey: dualidad y mapas entre subsecuencias ]. Berlín, Alemania: De Gruyter. ISBN 978-3-11-054662-0.Erratas + Código

• Hatcher, Allen. "Topología de números" (PDF) .Copia del libro en línea
• Bogomolny, Alexander . "Serie Farey". Cortar el nudo .
• Bogomolny, Alexander . "Árbol de la baya de la acacia". Corte del nudo .
• Pennestri, Ettore. "Una mesa Brocot de base 120".
• "Serie Farey", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Árbol de Stern-Brocot". MathWorld .
• Secuencia OEIS A005728 (Número de fracciones en la serie de Farey de orden n)
• Secuencia OEIS A006842 (Numeradores de la serie Farey de orden n)
• Secuencia OEIS A006843 (Denominadores de la serie de Farey de orden n)
• Archivado en Ghostarchive y Wayback Machine: Bonahon, Francis . Fracciones divertidas y círculos de Ford (video). Brady Haran . Consultado el 9 de junio de 2015 , a través de YouTube.