Nudo de rebanada

Un nudo de corte es un nudo matemático en el espacio tridimensional que delimita un disco incrustado en un espacio tetradimensional.

Se dice que un nudo es un nudo de rebanada topológica o un nudo de rebanada suave , si es el límite de un disco incrustado en la 4-bola , que es localmente plano o suave , respectivamente. Aquí usamos : la 3-esfera es el límite de la bola de cuatro dimensiones Cada nudo de rebanada suave es rebanada topológicamente porque un disco incrustado suavemente es localmente plano. Por lo general, los nudos de rebanada suave también se llaman simplemente rebanada. Ambos tipos de nudos de rebanada son importantes en la topología tridimensional y tetradimensional.${\displaystyle K\subconjunto S^{3}}$$Estilo de visualización B^{4}}$${\displaystyle S^{3}=\parcial B^{4}}$ ${\displaystyle S^{3}=\{\mathbf {x} \en \mathbb {R} ^{4}:|\mathbf {x} |=1\}}$ ${\displaystyle B^{4}=\{\mathbf {x} \en \mathbb {R} ^{4}:|\mathbf {x} |\leq 1\}.}$

Los nudos de rebanadas suaves a menudo se ilustran utilizando diagramas de nudos de cinta y es una pregunta abierta si existen nudos de rebanadas suaves que no sean nudos de cinta (′Conjetura de rebanada-cinta′).

Las condiciones localmente plano o suave son esenciales en la definición: para cada nudo podemos construir el cono sobre el nudo que es un disco en la bola 4 con la propiedad requerida con la excepción de que no es localmente plano o suave en la singularidad (aunque funciona para el nudo trivial).

Obsérvese que el disco de la ilustración de la derecha no tiene autointersecciones en el espacio cuatridimensional. Estas solo se producen en la proyección al espacio tridimensional. Por lo tanto, el disco está incrustado "correctamente" en cada punto, pero no en la singularidad (no es localmente plano allí).

Dos nudos orientados se dicen concordantes , si la suma conexa es slice. De la misma manera que antes, distinguimos topológicamente y suavemente concordantes. Con denotamos la imagen especular de donde además la orientación está invertida. La relación ′concordante′ es reflexiva porque es slice para cada nudo . También es posible demostrar que es transitiva: si es concordante con y es concordante con entonces es concordante con . Dado que la relación también es simétrica, es una relación de equivalencia . Las clases de equivalencia junto con la suma conexa de nudos como operación forman entonces un grupo abeliano que se llama grupo de concordancia de nudos (topológico o suave). El elemento neutro en este grupo es el conjunto de nudos slice (topológico o suave, respectivamente).$Estilo de visualización K_{1}, K_{2}$ ${\displaystyle K_{1}\sharp-K_{2}}$$Estilo de visualización: -K_{2}$$Estilo de visualización K2$${\displaystyle K\sostenido -K}$${\estilo de visualización K}$$Estilo de visualización K_{1}$$Estilo de visualización K2$$Estilo de visualización K2$$Estilo de visualización K3$$Estilo de visualización K_{1}$$Estilo de visualización K3$

Cada nudo de cinta es un nudo de corte suave porque, con excepción de las singularidades de cinta, el nudo ya delimita un disco incrustado (en el espacio tridimensional). Las singularidades de cinta pueden deformarse en un pequeño vecindario en el espacio tridimensional de modo que el disco quede incrustado.

Hay 21 nudos primos de rebanada no triviales con número de cruce . Estos son , , , , , , , , , , , , , , , , , , , y . Hasta este número de cruce no hay nudos de rebanada topológicamente que no sean de rebanada suave. ^[1] Sin embargo, a partir del cruce número 11 existe un ejemplo de este tipo: el nudo Conway (llamado así por John Horton Conway ) es un nudo de rebanada topológicamente pero no de rebanada suave. ^[2] Por otro lado, el nudo Kinoshita-Terasaka, un llamado ′ mutante ′ del nudo Conway, es de rebanada suave. Los nudos de torsión , a excepción del nudo trivial y el nudo Stevedore , no son de rebanada. ^[3] Se conocen todos los nudos de rebanada topológicamente y de rebanada suave con número de cruce . ^[4] Los nudos de corte compuestos hasta el cruce número 12 son, además de los de la forma y , los dos nudos más interesantes y . ^[5]${\displaystyle cr(K)\leq 10}$${\estilo de visualización 6_{1}}$$Estilo de visualización 8_{8}$${\estilo de visualización 8_{9}}$${\estilo de visualización 8_{20}}$$Estilo de visualización 9_{27}$${\estilo de visualización 9_{41}}$${\estilo de visualización 9_{46}}$${\estilo de visualización 10_{3}}$$Estilo de visualización 10_{22}$$estilo de visualización 10_{35}}$$estilo de visualización 10_{42}}$$estilo de visualización 10_{48}}$${\estilo de visualización 10_{75}}$$estilo de visualización 10_87$${\estilo de visualización 10_{99}}$$estilo de visualización 10_{123}}$$estilo de visualización 10_{129}}$$estilo de visualización 10_{137}}$$estilo de visualización 10_{140}}$$estilo de visualización 10_{153}}$$estilo de visualización 10_{155}}$ ${\estilo de visualización 6_{1}}$${\displaystyle cr(K)\leq 12}$${\displaystyle K\sostenido -K}$${\displaystyle 6_{1}\sharp 3_{1}\sharp -3_{1}}$${\displaystyle 3_{1}\sharp 8_{10}}$${\displaystyle 3_{1}\sharp 8_{11}}$

Las siguientes propiedades son válidas para nudos cortados topológicamente y de manera uniforme: El polinomio de Alexander de un nudo cortado se puede escribir como un polinomio de Laurent con coeficientes enteros (condición de Fox-Milnor). ^[6] De ello se deduce que el determinante del nudo ( ) es un número cuadrado.${\displaystyle \Delta(t)=f(t)f(t^{-1})}$ ${\estilo de visualización f}$${\displaystyle =\Delta (-1)}$

La firma es un invariante de las clases de concordancia y la firma de los nudos de corte es cero. Además, el mapa de firmas es un homomorfismo del grupo de concordancia a los números enteros : la firma de la suma de dos clases de concordancia es la suma de las dos firmas.

• De ello se deduce que el grupo de concordancia contiene elementos de orden infinito : La firma de un nudo de trébol es ±2 y la firma de la clase de concordancia de la suma conexa de tréboles es y, por lo tanto, no es 0.${\estilo de visualización n}$${\estilo de visualización \pm 2n}$
• El grupo de concordancia también contiene elementos de orden 2: El nudo en forma de ocho es anficario e invertible , y por lo tanto tenemos . En el grupo de concordancia encontramos . Como el determinante del nudo en forma de ocho es 5, que no es un número cuadrado, este nudo no es slice y se deduce que su orden en el grupo de concordancia es 2. Por supuesto, los nudos con un orden finito en el grupo de concordancia siempre tienen signatura 0.${\estilo de visualización 4_{1}}$$Estilo de visualización 4_{1}=-4_{1}}$${\displaystyle 4_{1}\sharp 4_{1}=4_{1}\sharp -4_{1}=0}$

Para ambas variantes del grupo de concordancia se desconoce si existen elementos de orden finito.${\estilo de visualización >2}$

Por otra parte, existen invariantes con diferentes propiedades para las dos variantes de concordancia: los nudos con polinomio de Alexander trivial ( ) siempre son topológicamente rebanadas, pero no necesariamente rebanadas suaves (el nudo de Conway es un ejemplo de esto). El s-invariante de Rasmussen se desvanece para rebanadas suaves, pero en general no para nudos topológicamente rebanadas. ^[7]${\displaystyle \Delta(t)=1}$

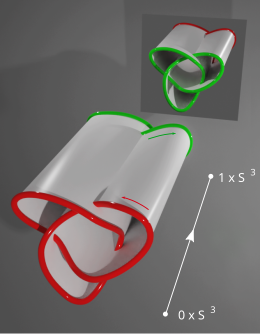
Como alternativa a la definición anterior de concordancia utilizando nudos de rebanada, también hay una segunda definición equivalente. Dos nudos orientados y son concordantes si son el límite de un cilindro (localmente plano o liso) (en el espacio de 4 dimensiones ). Las orientaciones de los dos nudos tienen que ser consistentes con la orientación del cilindro, que se ilustra en la tercera figura. El límite de son dos con diferentes orientaciones ^[8] y, por lo tanto, se muestran dos tréboles reflejados como límite del cilindro. Conectar los dos nudos cortando una tira del cilindro produce un disco, lo que muestra que para todos los nudos la suma conectada es rebanada. En ambas definiciones, un nudo es rebanada si y solo si es concordante con el nudo trivial.$Estilo de visualización K_{1}$$Estilo de visualización K2$${\displaystyle C=S^{1}\times [0,1]}$${\displaystyle S^{3}\times [0,1]}$${\displaystyle S^{3}\times [0,1]}$$Estilo de visualización S3$${\displaystyle K\sostenido -K}$

Esto también se puede ilustrar con la primera figura que aparece en la parte superior de este artículo: si se corta un pequeño disco en el mínimo local de la parte inferior izquierda, el límite de la superficie en este lugar es un nudo trivial y la superficie es un cilindro. En el otro extremo del cilindro tenemos un nudo de corte. Si el disco (o cilindro) está incrustado de forma suave, se puede deformar ligeramente hasta una denominada posición de Morse .

Esto es útil porque los puntos críticos con respecto a la función radial r tienen un significado geométrico. En los puntos de silla, se agregan o destruyen componentes triviales (movimientos de banda, también llamados fusión y fisión). Para los nudos de rebanada, cualquier número de estos movimientos de banda es posible, mientras que para los nudos de cinta solo pueden ocurrir fusiones y no se permiten fisiones.

En la ilustración de la derecha, la descripción geométrica de la concordancia se ha girado 90° y el parámetro r se ha renombrado como t. Este nombre se adapta bien a una interpretación temporal de una "película" de superficie.

Una definición análoga a la de los nudos slice se puede hacer con superficies de género mayor . El 4-género (también llamado ′género slice′) de un nudo se define, por tanto, como el género más pequeño de una superficie incrustada en el 4-espacio del que el nudo es el límite. Como antes, distinguimos el 4-género topológico y el liso. Los nudos con 4-género 0 son nudos slice porque un disco, la superficie más simple, tiene género 0. El 4-género es siempre más pequeño o igual al género del nudo porque este invariante se define utilizando superficies de Seifert que ya están incrustadas en el espacio tridimensional.

En la siguiente tabla se enumeran ejemplos de nudos con diferentes valores para su 4-género topológico y liso. El nudo Conway 11n34 es, como ya se ha mencionado, el primer ejemplo en las tablas de nudos de un nudo de corte topológico pero no liso. A juzgar por los valores de la tabla, podríamos concluir que el 4-género liso y el topológico siempre difieren en 1, cuando no son iguales. Sin embargo, este no es el caso y la diferencia puede ser arbitrariamente grande. ^[9] Sin embargo, no se sabe (a fecha de 2017) si hay nudos alternos con una diferencia > 1. ^[10]

	$estilo de visualización 10_{139}}$	$estilo de visualización 10_{145}}$	$estilo de visualización 10_{152}}$	$estilo de visualización 10_{154}}$	$estilo de visualización 10_{161}}$	${\estilo de visualización 11n34}$
4-género (liso)	4	2	4	3	3	1
4-género (arriba)	3	1	3	2	2	0

• Dale Rolfsen: Nudos y vínculos , Publish or Perish, 1976, Capítulo 8.E
• Charles Livingston: Teoría de nudos , Carus Mathematical Monographs, 1993
• Charles Livingston: Un estudio de la concordancia clásica de nudos , capítulo 7 en “Handbook of Knot Theory”, Elsevier, 2005

• Peter Teichner : Nudos de corte: teoría de nudos en la cuarta dimensión

• Concordancia de enlaces  : relación de equivalencia de enlaces más débil que la isotopía pero más fuerte que la homotopía