Producción en pareja

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Producción en pareja» – noticias  · periódicos  · libros  · académico  · JSTOR ( mayo de 2013 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Interacción luz-materia
Fenómenos de baja energía:
Efecto fotoeléctrico
Fenómenos de energía media:
Dispersión de Thomson
Dispersión Compton
Fenómenos de alta energía:
Producción en pareja
Fotodesintegración
Fotofisión
en a mi

La producción de pares es la creación de una partícula subatómica y su antipartícula a partir de un bosón neutro . Los ejemplos incluyen la creación de un electrón y un positrón , un muón y un antimuón , o un protón y un antiprotón . La producción de pares a menudo se refiere específicamente a un fotón que crea un par electrón-positrón cerca de un núcleo. Como la energía debe conservarse, para que se produzca la producción de pares, la energía entrante del fotón debe ser superior a un umbral de al menos la energía de masa en reposo total de las dos partículas creadas. (Como el electrón es la partícula elemental más ligera, por lo tanto, la de menor masa/energía, requiere los fotones menos energéticos de todos los posibles procesos de producción de pares). La conservación de la energía y el momento son las principales restricciones del proceso. ^[1] Todos los demás números cuánticos conservados ( momento angular , carga eléctrica , número leptónico ) de las partículas producidas deben sumar cero, por lo que las partículas creadas tendrán valores opuestos entre sí. Por ejemplo, si una partícula tiene una carga eléctrica de +1, la otra debe tener una carga eléctrica de −1, o si una partícula tiene una extrañeza de +1, entonces la otra debe tener una extrañeza de −1.

La probabilidad de producción de pares en las interacciones fotón-materia aumenta con la energía del fotón y también aumenta aproximadamente con el cuadrado del número atómico (y por lo tanto, el número de protones) del átomo cercano. ^[2]

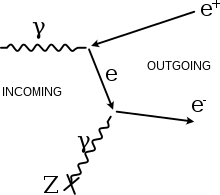
En el caso de fotones con alta energía ( escala MeV y superior), la producción de pares es el modo dominante de interacción de los fotones con la materia. Estas interacciones se observaron por primera vez en la cámara de nubes contracontrolada de Patrick Blackett , lo que le valió el Premio Nobel de Física en 1948. ^[3] Si el fotón está cerca de un núcleo atómico, la energía de un fotón se puede convertir en un par electrón-positrón:

(Z+)
gamma
→ 
mi⁻
 + 
mi⁺

La energía del fotón se convierte en masa de partícula de acuerdo con la ecuación de Einstein, E = mc2 ; donde E es la energía , m es la masa y c es la velocidad de la luz . El fotón debe tener ^una energía mayor que la suma de las energías de masa en reposo de un electrón y un positrón (2 × 511 keV = 1,022 MeV, lo que da como resultado una longitud de onda del fotón de1,2132  pm ) para que se produzca la producción. (Por lo tanto, la producción de pares no ocurre en las imágenes médicas de rayos X porque estos rayos X solo contienen ~ 150 keV). El fotón debe estar cerca de un núcleo para satisfacer la conservación del momento, ya que un par electrón-positrón producido en el espacio libre no puede satisfacer la conservación de la energía y el momento. ^[5] Debido a esto, cuando se produce la producción de pares, el núcleo atómico recibe algo de retroceso . El reverso de este proceso es la aniquilación electrón-positrón .

Estas propiedades se pueden derivar a través de la cinemática de la interacción. Utilizando la notación de cuatro vectores , la conservación de la energía y el momento antes y después de la interacción da: ^[6]

${\displaystyle p_{\gamma}=p_{{\text{e}}^{-}}+p_{{\text{e}}^{+}}+p_{\text{ʀ}}}$

¿Dónde está el retroceso del núcleo? Nótese el módulo de los cuatro vectores. ${\displaystyle p_{\text{ʀ}}}$

${\displaystyle A\equiv(A^{0},\mathbf {A})}$

es

${\displaystyle A^{2}=A^{\mu }A_{\mu }=-(A^{0})^{2}+\mathbf {A} \cdot \mathbf {A} }$

lo que implica que para todos los casos y . Podemos elevar al cuadrado la ecuación de conservación${\displaystyle (p_{\gamma })^{2}=0}$${\displaystyle (p_{{\text{e}}^{-}})^{2}=-m_{\text{e}}^{2}c^{2}}$

${\displaystyle (p_{\gamma })^{2}=(p_{{\text{e}}^{-}}+p_{{\text{e}}^{+}}+p_{\text{ʀ}})^{2}}$

Sin embargo, en la mayoría de los casos el retroceso del núcleo es pequeño comparado con la energía del fotón y puede despreciarse. Tomando esta aproximación y ampliando la relación restante${\displaystyle p_{R}\aproximadamente 0}$

${\displaystyle (p_{\gamma })^{2}\approx (p_{{\text{e}}^{-}})^{2}+2p_{{\text{e}}^{-}}p_{{\text{e}}^{+}}+(p_{{\text{e}}^{+}})^{2}}$

${\displaystyle -2\,m_{\text{e}}^{2}c^{2}+2\left(-{\frac {E^{2}}{c^{2}}}+\mathbf {p} _{{\text{e}}^{-}}\cdot \mathbf {p} _{{\text{e}}^{+}}\right)\approx 0}$

${\displaystyle 2\,(\gamma ^{2}-1)\,m_{\text{e}}^{2}\,c^{2}\,(\cos \theta _{\text{e}}-1)\approx 0}$

Por lo tanto, esta aproximación sólo puede satisfacerse si el electrón y el positrón se emiten en casi la misma dirección, es decir, .${\displaystyle \theta _{\text{e}}\aproximadamente 0}$

Esta derivación es una aproximación semiclásica. Se puede realizar una derivación exacta de la cinemática teniendo en cuenta la dispersión mecánica cuántica completa del fotón y el núcleo .

La transferencia de energía al electrón y al positrón en interacciones de producción de pares está dada por

${\displaystyle (E_{k}^{pp})_{\text{tr}}=h\nu -2\,m_{\text{e}}c^{2}}$

donde es la constante de Planck , es la frecuencia del fotón y es la masa en reposo combinada del electrón y el positrón. En general, el electrón y el positrón pueden emitirse con diferentes energías cinéticas, pero el promedio transferido a cada uno (ignorando el retroceso del núcleo) es${\estilo de visualización h}$${\estilo de visualización \nu}$${\displaystyle 2\,m_{\text{e}}c^{2}}$

${\displaystyle ({\bar {E}}_{k}^{pp})_{\text{tr}}={\frac {1}{2}}(h\nu -2\,m_{\text{e}}c^{2})}$

La forma analítica exacta de la sección eficaz de la producción de pares debe calcularse mediante electrodinámica cuántica en forma de diagramas de Feynman y da como resultado una función complicada. Para simplificar, la sección eficaz puede escribirse como:

${\displaystyle \sigma =\alpha \,r_{\text{e}}^{2}\,Z^{2}\,P(E,Z)}$

donde es la constante de estructura fina , es el radio clásico del electrón , es el número atómico del material y es una función de valor complejo que depende de la energía y el número atómico. Las secciones transversales se tabulan para diferentes materiales y energías.${\displaystyle \alpha }$${\displaystyle r_{\text{e}}}$${\displaystyle Z}$${\displaystyle P(E,Z)}$

En 2008, el láser Titán , apuntado a un objetivo de oro de un milímetro de espesor , se utilizó para generar pares positrones-electrones en grandes cantidades. ^[7]

La producción de pares se invoca en la explicación heurística de la radiación de Hawking hipotética . Según la mecánica cuántica , los pares de partículas aparecen y desaparecen constantemente como una espuma cuántica . En una región de fuertes fuerzas de marea gravitatorias , las dos partículas de un par a veces pueden separarse antes de que tengan la oportunidad de aniquilarse mutuamente . Cuando esto sucede en la región alrededor de un agujero negro , una partícula puede escapar mientras que su antipartícula compañera es capturada por el agujero negro.

La producción de pares es también el mecanismo detrás de la supuesta supernova de tipo de inestabilidad de pares , en la que la producción de pares reduce repentinamente la presión dentro de una estrella supergigante , lo que lleva a una implosión parcial y luego a una combustión termonuclear explosiva. Se plantea la hipótesis de que la supernova SN 2006gy fue una supernova de tipo de producción de pares .

• Proceso Breit-Wheeler
• Ecuación de Dirac
• Creación de materia
• Efecto Meitner-Hupfeld
• Efecto Landau-Pomeranchuk-Migdal
• Física de dos fotones

• Teoría de la producción de pares libres ligados por impacto de fotones