Sección transversal (física)

Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . Ayúdenos a mejorar este artículo introduciendo citas más precisas. ( enero de 2022 ) ( aprenda cómo y cuándo eliminar este mensaje )

En física, la sección transversal es una medida de la probabilidad de que se produzca un proceso específico en una colisión de dos partículas. Por ejemplo, la sección transversal de Rutherford es una medida de la probabilidad de que una partícula alfa se desvíe en un ángulo determinado durante una interacción con un núcleo atómico . La sección transversal se denota típicamente σ ( sigma ) y se expresa en unidades de área, más específicamente en barns . En cierto modo, se puede pensar en ella como el tamaño del objeto que la excitación debe golpear para que se produzca el proceso, pero más exactamente, es un parámetro de un proceso estocástico .

Cuando dos partículas discretas interactúan en la física clásica, su sección transversal mutua es el área transversal a su movimiento relativo dentro del cual deben encontrarse para dispersarse entre sí. Si las partículas son esferas inelásticas duras que interactúan solo al entrar en contacto, su sección transversal de dispersión está relacionada con su tamaño geométrico. Si las partículas interactúan a través de alguna fuerza de acción a distancia, como el electromagnetismo o la gravedad , su sección transversal de dispersión es generalmente mayor que su tamaño geométrico.

Cuando una sección transversal se especifica como el límite diferencial de una función de alguna variable de estado final, como el ángulo o la energía de la partícula, se denomina sección transversal diferencial (consulte la discusión detallada a continuación). Cuando una sección transversal se integra sobre todos los ángulos de dispersión (y posiblemente otras variables), se denomina sección transversal total o sección transversal total integrada . Por ejemplo, en la dispersión de Rayleigh , la intensidad dispersada en los ángulos hacia adelante y hacia atrás es mayor que la intensidad dispersada lateralmente, por lo que la sección transversal de dispersión diferencial hacia adelante es mayor que la sección transversal diferencial perpendicular, y al sumar todas las secciones transversales infinitesimales sobre todo el rango de ángulos con cálculo integral, podemos encontrar la sección transversal total.

Las secciones transversales de dispersión se pueden definir en física nuclear , atómica y de partículas para colisiones de haces acelerados de un tipo de partícula con objetivos (estacionarios o móviles) de un segundo tipo de partícula. La probabilidad de que ocurra una reacción dada es proporcional a su sección transversal. Por lo tanto, especificar la sección transversal para una reacción dada es un indicador de la probabilidad de que ocurra un proceso de dispersión dado.

La velocidad de reacción medida de un proceso determinado depende en gran medida de variables experimentales, como la densidad del material objetivo, la intensidad del haz, la eficiencia de detección del aparato o el ajuste del ángulo del aparato de detección. Sin embargo, estas cantidades se pueden tener en cuenta, lo que permite medir la sección transversal de colisión subyacente de dos partículas.

Las secciones eficaces de dispersión diferencial y total se encuentran entre las cantidades mensurables más importantes en la física nuclear , atómica y de partículas .

En el caso de la dispersión de luz de una partícula, la sección transversal especifica la cantidad de potencia óptica dispersada a partir de la luz de una irradiancia dada (potencia por área). Es importante señalar que, aunque la sección transversal tiene las mismas unidades que el área, la sección transversal puede no corresponder necesariamente al tamaño físico real del objetivo proporcionado por otras formas de medición. No es raro que el área de la sección transversal real de un objeto que se dispersa sea mucho mayor o menor que la sección transversal relativa a algún proceso físico. Por ejemplo, las nanopartículas plasmónicas pueden tener secciones transversales de dispersión de luz para frecuencias particulares que son mucho mayores que sus áreas de sección transversal reales.

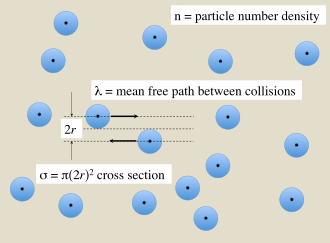
En un gas de partículas de tamaño finito se producen colisiones entre partículas que dependen del tamaño de su sección transversal. La distancia media que recorre una partícula entre colisiones depende de la densidad de partículas del gas. Estas cantidades están relacionadas por

${\displaystyle \sigma ={\frac {1}{n\lambda }},}$

dónde

σ es la sección transversal de una colisión de dos partículas ( unidad SI : m ² ),

λ es el camino libre medio entre colisiones (unidad SI: m),

n es la densidad numérica de las partículas objetivo (unidad SI: m ⁻³ ).

Si las partículas en el gas pueden tratarse como esferas duras de radio r que interactúan por contacto directo, como se ilustra en la Figura 1, entonces la sección transversal efectiva para la colisión de un par es

${\displaystyle \sigma =\pi \left(2r\right)^{2}}$

Si las partículas en el gas interactúan mediante una fuerza con un rango mayor que su tamaño físico, entonces la sección transversal es un área efectiva más grande que puede depender de una variedad de variables, como la energía de las partículas.

Las secciones transversales se pueden calcular para colisiones atómicas, pero también se utilizan en el ámbito subatómico. Por ejemplo, en física nuclear, un "gas" de neutrones de baja energía colisiona con núcleos en un reactor u otro dispositivo nuclear, con una sección transversal que depende de la energía y, por lo tanto, también con un camino libre medio bien definido entre colisiones.

Si un haz de partículas entra en una capa delgada de material de espesor d z , el flujo Φ del haz disminuirá en dΦ de acuerdo con

${\displaystyle {\frac {\mathrm {d} \Phi }{\mathrm {d} z}}=-n\sigma \Phi ,}$

donde σ es la sección transversal total de todos los eventos, incluyendo dispersión , absorción o transformación a otra especie. La densidad numérica volumétrica de los centros de dispersión se designa por n . Al resolver esta ecuación se muestra la atenuación exponencial de la intensidad del haz:

${\displaystyle \Phi =\Phi _{0}e^{-n\sigma z},}$

donde Φ ₀ es el flujo inicial y z es el espesor total del material. Para la luz, esto se denomina ley de Beer-Lambert .

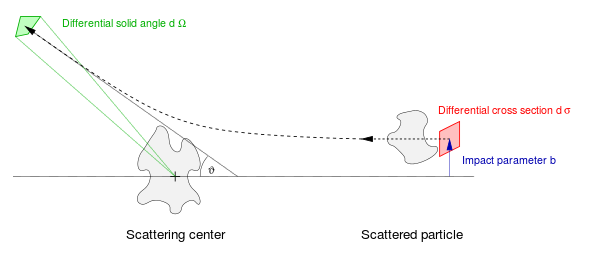
Consideremos una medición clásica en la que una partícula individual se dispersa a partir de una partícula objetivo estacionaria. Convencionalmente, se utiliza un sistema de coordenadas esféricas , con el objetivo colocado en el origen y el eje z de este sistema de coordenadas alineado con el haz incidente. El ángulo θ es el ángulo de dispersión , medido entre el haz incidente y el haz disperso, y φ es el ángulo azimutal .

El parámetro de impacto b es el desplazamiento perpendicular de la trayectoria de la partícula entrante, y la partícula saliente emerge en un ángulo θ . Para una interacción dada ( coulombiana , magnética , gravitacional , de contacto, etc.), el parámetro de impacto y el ángulo de dispersión tienen una dependencia funcional definida uno a uno entre sí. Generalmente, el parámetro de impacto no se puede controlar ni medir de un evento a otro y se supone que toma todos los valores posibles cuando se promedia sobre muchos eventos de dispersión. El tamaño diferencial de la sección transversal es el elemento de área en el plano del parámetro de impacto, es decir, d σ = b d φ d b . El rango angular diferencial de la partícula dispersa en el ángulo θ es el elemento de ángulo sólido dΩ = sen θ d θ d φ . La sección transversal diferencial es el cociente de estas cantidades, ⁠dσ​/dΩ⁠ .

Es una función del ángulo de dispersión (y por lo tanto también del parámetro de impacto), más otros observables como el momento de la partícula entrante. La sección transversal diferencial siempre se considera positiva, aunque los parámetros de impacto mayores generalmente producen una menor desviación. En situaciones de simetría cilíndrica (alrededor del eje del haz), el ángulo azimutal φ no cambia por el proceso de dispersión, y la sección transversal diferencial se puede escribir como

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} (\cos \theta )}}=\int _{0}^{2\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\,\mathrm {d} \varphi }$.

En situaciones en las que el proceso de dispersión no es azimutalmente simétrico, como cuando el haz o las partículas objetivo poseen momentos magnéticos orientados perpendicularmente al eje del haz, la sección transversal diferencial también debe expresarse como una función del ángulo azimutal.

Para la dispersión de partículas de flujo incidente F _inc desde un objetivo estacionario que consta de muchas partículas, la sección transversal diferencialdσ​/dΩ⁠ en un ángulo ( θ , φ ) está relacionado con el flujo de detección de partículas dispersas F _out ( θ , φ ) en partículas por unidad de tiempo por

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}(\theta ,\varphi )={\frac {1}{nt\Delta \Omega }}{\frac {F_{\text{out}}(\theta ,\varphi )}{F_{\text{inc}}}}.}$

Aquí ΔΩ es el tamaño angular finito del detector (unidad del SI: sr ), n es la densidad numérica de las partículas objetivo (unidad del SI: m ⁻³ ) y t es el espesor del objetivo estacionario (unidad del SI: m). Esta fórmula supone que el objetivo es lo suficientemente delgado como para que cada partícula del haz interactúe con, como máximo, una partícula objetivo.

La sección transversal total σ se puede recuperar integrando la sección transversal diferencial ⁠dσ​/dΩ⁠ sobre el ángulo sólido completo ( 4π estereorradianes):

${\displaystyle \sigma =\oint _{4\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\,\mathrm {d} \Omega =\int _{0}^{2\pi }\int _{0}^{\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi .}$

Es común omitir el calificador "diferencial" cuando el tipo de sección transversal se puede inferir del contexto. En este caso, σ puede denominarse sección transversal integral o sección transversal total . El último término puede resultar confuso en contextos en los que intervienen varios eventos, ya que "total" también puede referirse a la suma de las secciones transversales de todos los eventos.

La sección eficaz diferencial es una magnitud extremadamente útil en muchos campos de la física, ya que su medición puede revelar una gran cantidad de información sobre la estructura interna de las partículas en cuestión. Por ejemplo, la sección eficaz diferencial de la dispersión de Rutherford proporcionó pruebas sólidas de la existencia del núcleo atómico.

En lugar del ángulo sólido, se puede utilizar la transferencia de momento como variable independiente de las secciones transversales diferenciales.

Las secciones transversales diferenciales en dispersión inelástica contienen picos de resonancia que indican la creación de estados metaestables y contienen información sobre su energía y vida útil.

En el formalismo independiente del tiempo de la dispersión cuántica , la función de onda inicial (antes de la dispersión) se toma como una onda plana con un momento definido k :

${\displaystyle \phi _{-}(\mathbf {r} )\;{\stackrel {r\to \infty }{\longrightarrow }}\;e^{ikz},}$

donde z y r son las coordenadas relativas entre el proyectil y el objetivo. La flecha indica que esto solo describe el comportamiento asintótico de la función de onda cuando el proyectil y el objetivo están demasiado separados para que la interacción tenga algún efecto.

Después de que se produce la dispersión, se espera que la función de onda adopte la siguiente forma asintótica:

${\displaystyle \phi _{+}(\mathbf {r} )\;{\stackrel {r\to \infty }{\longrightarrow }}\;f(\theta ,\phi ){\frac {e^{ikr}}{r}},}$

donde f es una función de las coordenadas angulares conocida como amplitud de dispersión . Esta forma general es válida para cualquier interacción de corto alcance que conserve la energía. No es válida para interacciones de largo alcance, por lo que existen complicaciones adicionales al tratar con interacciones electromagnéticas.

La función de onda completa del sistema se comporta asintóticamente como la suma

${\displaystyle \phi (\mathbf {r} )\;{\stackrel {r\to \infty }{\longrightarrow }}\;\phi _{-}(\mathbf {r} )+\phi _{+}(\mathbf {r} ).}$

La sección transversal diferencial está relacionada con la amplitud de dispersión:

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}(\theta ,\phi )={\bigl |}f(\theta ,\phi ){\bigr |}^{2}.}$

Esto tiene una interpretación simple: la densidad de probabilidad de encontrar el proyectil disperso en un ángulo dado.

Por lo tanto, una sección transversal es una medida del área superficial efectiva vista por las partículas que chocan y, como tal, se expresa en unidades de área. La sección transversal de dos partículas (es decir, observada cuando las dos partículas chocan entre sí) es una medida del evento de interacción entre las dos partículas. La sección transversal es proporcional a la probabilidad de que ocurra una interacción; por ejemplo, en un experimento de dispersión simple, el número de partículas dispersadas por unidad de tiempo (corriente de partículas dispersadas I _r ) depende solo del número de partículas incidentes por unidad de tiempo (corriente de partículas incidentes I _i ), las características del objetivo (por ejemplo, el número de partículas por unidad de superficie N ) y el tipo de interacción. Para Nσ ≪ 1 tenemos

${\displaystyle {\begin{aligned}I_{\text{r}}&=I_{\text{i}}N\sigma ,\\\sigma &={\frac {I_{\text{r}}}{I_{\text{i}}}}{\frac {1}{N}}\\&={\text{probability of interaction}}\times {\frac {1}{N}}.\end{aligned}}}$

Si las masas y momentos reducidos del sistema en colisión son m _i , p _i y m _f , p _f antes y después de la colisión respectivamente, la sección transversal diferencial está dada por ^{[ aclaración necesaria ]}

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}=\left(2\pi \right)^{4}m_{\text{i}}m_{\text{f}}{\frac {p_{\text{f}}}{p_{\text{i}}}}{\bigl |}T_{{\text{f}}{\text{i}}}{\bigr |}^{2},}$

donde la matriz T en la capa se define por

${\displaystyle S_{{\text{f}}{\text{i}}}=\delta _{{\text{f}}{\text{i}}}-2\pi i\delta \left(E_{\text{f}}-E_{\text{i}}\right)\delta \left(\mathbf {p} _{\text{i}}-\mathbf {p} _{\text{f}}\right)T_{{\text{f}}{\text{i}}}}$

en términos de la matriz S. Aquí δ es la función delta de Dirac . El cálculo de la matriz S es el objetivo principal de la teoría de dispersión .

Aunque la unidad SI de las secciones transversales totales es m ² , en la práctica se suele utilizar una unidad más pequeña.

En física nuclear y de partículas, la unidad convencional es el barn b , donde 1 b = 10 ⁻²⁸  m ² = 100  fm ² . ^{[1] También se utilizan ampliamente unidades} con prefijo más pequeñas , como mb y μb . En consecuencia, la sección transversal diferencial se puede medir en unidades como mb/sr.

Cuando la radiación dispersa es luz visible, es convencional medir la longitud del recorrido en centímetros . Para evitar la necesidad de factores de conversión, la sección eficaz de dispersión se expresa en cm ² y la concentración numérica en cm ⁻³ . La medición de la dispersión de la luz visible se conoce como nefelometría y es efectiva para partículas de 2 a 50  μm de diámetro: como tal, se usa ampliamente en meteorología y en la medición de la contaminación atmosférica .

La dispersión de rayos X también se puede describir en términos de secciones transversales de dispersión, en cuyo caso el ångström cuadrado es una unidad conveniente: 1 Å ² = 10 ⁻²⁰  m ² =10 000  pm ² = 10 ⁸  b. La suma de las secciones eficaces de dispersión, fotoeléctrica y de producción de pares (en barns) se representa gráficamente como el "coeficiente de atenuación atómica" (haz angosto), en barns. ^[2]

En el caso de la luz, como en otros entornos, la sección transversal de dispersión de las partículas es generalmente diferente de la sección transversal geométrica de la partícula y depende de la longitud de onda de la luz y de la permitividad , la forma y el tamaño de la partícula. La cantidad total de dispersión en un medio disperso es proporcional al producto de la sección transversal de dispersión y la cantidad de partículas presentes.

En la interacción de la luz con las partículas se producen muchos procesos, cada uno con su propia sección eficaz, entre ellos la absorción , la dispersión y la fotoluminiscencia . La suma de las secciones eficaces de absorción y dispersión se denomina a veces sección eficaz de atenuación o extinción.

${\displaystyle \sigma =\sigma _{\text{abs}}+\sigma _{\text{sc}}+\sigma _{\text{lum}}.}$

La sección eficaz de extinción total está relacionada con la atenuación de la intensidad de la luz a través de la ley de Beer-Lambert , que dice que la atenuación es proporcional a la concentración de partículas:

${\displaystyle A_{\lambda }=Cl\sigma ,}$

donde A _λ es la atenuación a una longitud de onda dada λ , C es la concentración de partículas como densidad numérica y l es la longitud del recorrido . La absorbancia de la radiación es el logaritmo ( decádico o, más habitualmente, natural ) del recíproco de la transmitancia T : ^[3]

${\displaystyle A_{\lambda }=-\log {\mathcal {T}}.}$

La combinación de las secciones eficaces de dispersión y absorción de esta manera a menudo es necesaria debido a la incapacidad de distinguirlas experimentalmente, y se han hecho muchos esfuerzos de investigación para desarrollar modelos que permitan distinguirlas, siendo la teoría de Kubelka-Munk una de las más importantes en esta área.

Las secciones transversales que se calculan comúnmente utilizando la teoría de Mie incluyen coeficientes de eficiencia para las secciones transversales de extinción , dispersión y absorción . Estas se normalizan mediante las secciones transversales geométricas de la partícula como La sección transversal se define por ${\textstyle Q_{\text{ext}}}$${\textstyle Q_{\text{sc}}}$${\textstyle Q_{\text{abs}}}$${\textstyle \sigma _{\text{geom}}=\pi a^{2}}$$${\displaystyle Q_{\alpha }={\frac {\sigma _{\alpha }}{\sigma _{\text{geom}}}},\qquad \alpha ={\text{ext}},{\text{sc}},{\text{abs}}.}$$

${\displaystyle \sigma _{\alpha }={\frac {W_{\alpha }}{I_{\text{inc}}}}}$

donde es el flujo de energía a través de la superficie circundante y es la intensidad de la onda incidente. Para una onda plana, la intensidad será , donde es la impedancia del medio receptor .${\displaystyle \left[W_{\alpha }\right]=\left[{\text{W}}\right]}$${\displaystyle \left[I_{\text{inc}}\right]=\left[{\frac {\text{W}}{{\text{m}}^{2}}}\right]}$${\displaystyle I_{\text{inc}}=|\mathbf {E} |^{2}/(2\eta )}$${\displaystyle \eta ={\sqrt {\mu \mu _{0}/(\varepsilon \varepsilon _{0})}}}$

El enfoque principal se basa en lo siguiente: primero, construimos una esfera imaginaria de radio (superficie ) alrededor de la partícula (el dispersor). La tasa neta de energía electromagnética que cruza la superficie es${\displaystyle r}$${\displaystyle A}$${\displaystyle A}$

${\displaystyle W_{\text{a}}=-\oint _{A}\mathbf {\Pi } \cdot {\hat {\mathbf {r} }}dA}$

donde es el vector de Poynting promediado en el tiempo. Si la energía se absorbe dentro de la esfera, de lo contrario se crea energía dentro de la esfera. No consideraremos este caso aquí. Si el medio anfitrión no absorbe, la energía debe ser absorbida por la partícula. Descomponemos el campo total en partes incidentes y dispersas , y lo mismo para el campo magnético . Por lo tanto, podemos descomponer en los tres términos , donde${\textstyle \mathbf {\Pi } ={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} ^{*}\times \mathbf {H} \right]}$${\displaystyle W_{\text{a}}>0}$${\displaystyle \mathbf {E} =\mathbf {E} _{\text{i}}+\mathbf {E} _{\text{s}}}$${\displaystyle \mathbf {H} }$${\displaystyle W_{a}}$${\displaystyle W_{\text{a}}=W_{\text{i}}-W_{\text{s}}+W_{\text{ext}}}$

${\displaystyle W_{\text{i}}=-\oint _{A}\mathbf {\Pi } _{\text{i}}\cdot {\hat {\mathbf {r} }}dA\equiv 0,\qquad W_{\text{s}}=\oint _{A}\mathbf {\Pi } _{\text{s}}\cdot {\hat {\mathbf {r} }}dA,\qquad W_{\text{ext}}=\oint _{A}\mathbf {\Pi } _{\text{ext}}\cdot {\hat {\mathbf {r} }}dA.}$

donde , , y . ${\displaystyle \mathbf {\Pi } _{\text{i}}={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} _{\text{i}}^{*}\times \mathbf {H} _{\text{i}}\right]}$${\displaystyle \mathbf {\Pi } _{\text{s}}={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} _{\text{s}}^{*}\times \mathbf {H} _{\text{s}}\right]}$${\displaystyle \mathbf {\Pi } _{\text{ext}}={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} _{s}^{*}\times \mathbf {H} _{i}+\mathbf {E} _{i}^{*}\times \mathbf {H} _{s}\right]}$

Todo el campo se puede descomponer en la serie de armónicos esféricos vectoriales (VSH) . Después de eso, se pueden tomar todas las integrales. En el caso de una esfera uniforme de radio , permitividad y permeabilidad , el problema tiene una solución precisa. ^[4] Los coeficientes de dispersión y extinción son donde . Estos están conectados como${\displaystyle a}$${\displaystyle \varepsilon }$${\displaystyle \mu }$$${\displaystyle Q_{\text{sc}}={\frac {2}{k^{2}a^{2}}}\sum _{n=1}^{\infty }(2n+1)(|a_{n}|^{2}+|b_{n}|^{2})}$$ $${\displaystyle Q_{\text{ext}}={\frac {2}{k^{2}a^{2}}}\sum _{n=1}^{\infty }(2n+1)\Re (a_{n}+b_{n})}$$${\textstyle k=n_{\text{host}}k_{0}}$$${\displaystyle \sigma _{\text{ext}}=\sigma _{\text{sc}}+\sigma _{\text{abs}}\qquad {\text{or}}\qquad Q_{\text{ext}}=Q_{\text{sc}}+Q_{\text{abs}}}$$

Supongamos que una partícula admite únicamente modos dipolares eléctricos y magnéticos con polarizabilidades y (aquí utilizamos la notación de polarizabilidad magnética a la manera de Bekshaev et al. ^{[5] [6]} en lugar de la notación de Nieto-Vesperinas et al. ^[7] ) expresada a través de los coeficientes de Mie como Entonces las secciones eficaces están dadas por y, finalmente, las secciones eficaces de absorción eléctrica y magnética son y${\textstyle \mathbf {p} =\alpha ^{e}\mathbf {E} }$${\textstyle \mathbf {m} =(\mu \mu _{0})^{-1}\alpha ^{m}\mathbf {H} }$$${\displaystyle \alpha ^{e}=4\pi \varepsilon _{0}\cdot i{\frac {3\varepsilon }{2k^{3}}}a_{1},\qquad \alpha ^{m}=4\pi \mu _{0}\cdot i{\frac {3\mu }{2k^{3}}}b_{1}.}$$$${\displaystyle \sigma _{\text{ext}}=\sigma _{\text{ext}}^{\text{(e)}}+\sigma _{\text{ext}}^{\text{(m)}}={\frac {1}{4\pi \varepsilon \varepsilon _{0}}}\cdot 4\pi k\Im (\alpha ^{e})+{\frac {1}{4\pi \mu \mu _{0}}}\cdot 4\pi k\Im (\alpha ^{m})}$$ $${\displaystyle \sigma _{\text{sc}}=\sigma _{\text{sc}}^{\text{(e)}}+\sigma _{\text{sc}}^{\text{(m)}}={\frac {1}{(4\pi \varepsilon \varepsilon _{0})^{2}}}\cdot {\frac {8\pi }{3}}k^{4}|\alpha ^{e}|^{2}+{\frac {1}{(4\pi \mu \mu _{0})^{2}}}\cdot {\frac {8\pi }{3}}k^{4}|\alpha ^{m}|^{2}}$$${\textstyle \sigma _{\text{abs}}=\sigma _{\text{abs}}^{\text{(e)}}+\sigma _{\text{abs}}^{\text{(m)}}}$$${\displaystyle \sigma _{\text{abs}}^{\text{(e)}}={\frac {1}{4\pi \varepsilon \varepsilon _{0}}}\cdot 4\pi k\left[\Im (\alpha ^{e})-{\frac {k^{3}}{6\pi \varepsilon \varepsilon _{0}}}|\alpha ^{e}|^{2}\right]}$$$${\displaystyle \sigma _{\text{abs}}^{\text{(m)}}={\frac {1}{4\pi \mu \mu _{0}}}\cdot 4\pi k\left[\Im (\alpha ^{m})-{\frac {k^{3}}{6\pi \mu \mu _{0}}}|\alpha ^{m}|^{2}\right]}$$

Para el caso de una partícula sin ganancia interna, es decir, no se emite energía internamente por la partícula ( ), tenemos un caso particular del teorema óptico La igualdad ocurre para partículas no absorbentes, es decir, para .${\textstyle \sigma _{\text{abs}}>0}$ $${\displaystyle {\frac {1}{4\pi \varepsilon \varepsilon _{0}}}\Im (\alpha ^{e})+{\frac {1}{4\pi \mu \mu _{0}}}\Im (\alpha ^{m})\geq {\frac {2k^{3}}{3}}\left[{\frac {|\alpha ^{e}|^{2}}{(4\pi \varepsilon \varepsilon _{0})^{2}}}+{\frac {|\alpha ^{m}|^{2}}{(4\pi \mu \mu _{0})^{2}}}\right]}$$${\textstyle \Im (\varepsilon )=\Im (\mu )=0}$

En el contexto de la dispersión de la luz sobre cuerpos extensos, la sección transversal de dispersión, σ _sc , describe la probabilidad de que la luz sea dispersada por una partícula macroscópica. En general, la sección transversal de dispersión es diferente de la sección transversal geométrica de una partícula, ya que depende de la longitud de onda de la luz y de la permitividad , además de la forma y el tamaño de la partícula. La cantidad total de dispersión en un medio disperso está determinada por el producto de la sección transversal de dispersión y la cantidad de partículas presentes. En términos de área, la sección transversal total ( σ ) es la suma de las secciones transversales debidas a la absorción , la dispersión y la luminiscencia :

${\displaystyle \sigma =\sigma _{\text{abs}}+\sigma _{\text{sc}}+\sigma _{\text{lum}}.}$

La sección transversal total está relacionada con la absorbancia de la intensidad de la luz a través de la ley de Beer-Lambert , que dice que la absorbancia es proporcional a la concentración: A _λ = Clσ , donde A _λ es la absorbancia a una longitud de onda dada λ , C es la concentración como densidad numérica y l es la longitud del camino . La extinción o absorbancia de la radiación es el logaritmo ( decádico o, más habitualmente, natural ) del recíproco de la transmitancia T : ^[3]

${\displaystyle A_{\lambda }=-\log {\mathcal {T}}.}$

No existe una relación simple entre la sección transversal de dispersión y el tamaño físico de las partículas, ya que la sección transversal de dispersión depende de la longitud de onda de la radiación utilizada. Esto se puede ver al observar un halo que rodea la Luna en una noche con bastante niebla: los fotones de luz roja experimentan una mayor área de sección transversal de gotas de agua que los fotones de mayor energía. El halo alrededor de la Luna tiene, por lo tanto, un perímetro de luz roja debido a que los fotones de menor energía se dispersan más lejos del centro de la Luna. Los fotones del resto del espectro visible quedan dentro del centro del halo y se perciben como luz blanca.

La sección eficaz de dispersión está relacionada con el rango meteorológico L _V :

${\displaystyle L_{\text{V}}={\frac {3.9}{C\sigma _{\text{scat}}}}.}$

La cantidad Cσ _scat a veces se denota b _scat , el coeficiente de dispersión por unidad de longitud. ^[8]

Las siguientes ecuaciones se aplican a dos esferas duras que experimentan una colisión perfectamente elástica. ^[9] Sean R y r los radios del centro de dispersión y de la esfera dispersa, respectivamente. La sección transversal diferencial es

${\displaystyle {\frac {d\sigma }{d\Omega }}={\frac {R^{2}}{4}},}$

y la sección transversal total es

${\displaystyle \sigma _{\text{tot}}=\pi \left(r+R\right)^{2}.}$

En otras palabras, la sección transversal de dispersión total es igual al área del círculo (con radio r + R ) dentro del cual debe llegar el centro de masa de la esfera entrante para que se desvíe.

En la dispersión de Rutherford , una partícula incidente con carga q y energía E se dispersa desde una partícula fija con carga Q. La sección transversal diferencial es

${\displaystyle {\frac {d\sigma }{d\Omega }}=\left({\frac {q\,Q}{16\pi \varepsilon _{0}E\sin ^{2}(\theta /2)}}\right)^{2}}$

donde es la permitividad del vacío . ^[10] La sección transversal total es infinita a menos que se aplique un límite para ángulos de dispersión pequeños. ^[11] Esto se debe al largo rango del potencial de Coulomb.${\displaystyle \varepsilon _{0}}$${\displaystyle \theta }$${\displaystyle 1/r}$

El siguiente ejemplo trata de un haz de luz que se dispersa desde un círculo con radio r y un límite perfectamente reflectante. El haz consta de una densidad uniforme de rayos paralelos, y la interacción haz-círculo se modela dentro del marco de la óptica geométrica . Debido a que el problema es genuinamente bidimensional, la sección transversal tiene unidad de longitud (por ejemplo, metro). Sea α el ángulo entre el rayo de luz y el radio que une el punto de reflexión del rayo con el punto central del espejo. Entonces, el aumento del elemento de longitud perpendicular al haz es

${\displaystyle \mathrm {d} x=r\cos \alpha \,\mathrm {d} \alpha .}$

El ángulo de reflexión de este rayo con respecto al rayo entrante es 2 α , y el ángulo de dispersión es

${\displaystyle \theta =\pi -2\alpha .}$

La relación diferencial entre la intensidad incidente y reflejada I es

${\displaystyle I\,\mathrm {d} \sigma =I\,\mathrm {d} x(x)=Ir\cos \alpha \,\mathrm {d} \alpha =I{\frac {r}{2}}\sin \left({\frac {\theta }{2}}\right)\,\mathrm {d} \theta =I{\frac {\mathrm {d} \sigma }{\mathrm {d} \theta }}\,\mathrm {d} \theta .}$

La sección transversal diferencial es por lo tanto ( dΩ = d θ )

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \theta }}={\frac {r}{2}}\sin \left({\frac {\theta }{2}}\right).}$

Su máximo en θ = π corresponde a la dispersión hacia atrás, y su mínimo en θ = 0 corresponde a la dispersión desde el borde del círculo directamente hacia adelante. Esta expresión confirma las expectativas intuitivas de que el círculo del espejo actúa como una lente divergente . La sección transversal total es igual al diámetro del círculo:

${\displaystyle \sigma =\int _{0}^{2\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \theta }}\,\mathrm {d} \theta =\int _{0}^{2\pi }{\frac {r}{2}}\sin \left({\frac {\theta }{2}}\right)\,\mathrm {d} \theta =2r.}$

El resultado del ejemplo anterior se puede utilizar para resolver el problema análogo en tres dimensiones, es decir, la dispersión desde una esfera perfectamente reflectante de radio a .

El plano perpendicular al haz de luz incidente se puede parametrizar mediante las coordenadas cilíndricas r y φ . En cualquier plano del rayo incidente y del reflejado podemos escribir (del ejemplo anterior):

${\displaystyle {\begin{aligned}r&=a\sin \alpha ,\\\mathrm {d} r&=a\cos \alpha \,\mathrm {d} \alpha ,\end{aligned}}}$

mientras que el elemento del área de impacto es

${\displaystyle \mathrm {d} \sigma =\mathrm {d} r(r)\times r\,\mathrm {d} \varphi ={\frac {a^{2}}{2}}\sin \left({\frac {\theta }{2}}\right)\cos \left({\frac {\theta }{2}}\right)\,\mathrm {d} \theta \,\mathrm {d} \varphi .}$

En coordenadas esféricas,

${\displaystyle \mathrm {d} \Omega =\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi .}$

Junto con la identidad trigonométrica

${\displaystyle \sin \theta =2\sin \left({\frac {\theta }{2}}\right)\cos \left({\frac {\theta }{2}}\right),}$

Nosotros obtenemos

${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}={\frac {a^{2}}{4}}.}$

La sección transversal total es

${\displaystyle \sigma =\oint _{4\pi }{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}\,\mathrm {d} \Omega =\pi a^{2}.}$

• Sección transversal nuclear
• Sección transversal de dispersión
• OIEA – Servicios de datos nucleares
• BNL – Centro Nacional de Datos Nucleares
• Particle Data Group – La revisión de la física de partículas
• Libro de oro de la IUPAC: definición: sección transversal de reacción
• Libro de oro de la IUPAC: definición: sección transversal de colisión
• Trazador de secciones transversales ShimPlotWell para datos nucleares