Rigidez estructural

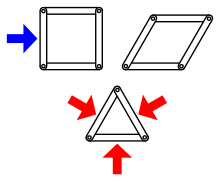
En geometría discreta y mecánica , la rigidez estructural es una teoría combinatoria para predecir la flexibilidad de conjuntos formados por cuerpos rígidos conectados por enlaces flexibles o bisagras .

La rigidez es la propiedad de una estructura de no doblarse ni flexionarse bajo una fuerza aplicada. El opuesto de la rigidez es la flexibilidad . En la teoría de la rigidez estructural, las estructuras están formadas por conjuntos de objetos que son en sí mismos cuerpos rígidos, que a menudo se supone que adoptan formas geométricas simples, como barras rectas (segmentos de línea), con pares de objetos conectados por bisagras flexibles. Una estructura es rígida si no puede flexionarse; es decir, si no hay un movimiento continuo de la estructura que preserve la forma de sus componentes rígidos y el patrón de sus conexiones en las bisagras.

Existen dos tipos de rigidez esencialmente diferentes. La rigidez finita o macroscópica significa que la estructura no se doblará, plegará ni se doblará en una cantidad positiva. La rigidez infinitesimal significa que la estructura no se doblará ni siquiera en una cantidad que sea demasiado pequeña para ser detectada incluso en teoría. (Técnicamente, eso significa que ciertas ecuaciones diferenciales no tienen soluciones distintas de cero). La importancia de la rigidez finita es obvia, pero la rigidez infinitesimal también es crucial porque la flexibilidad infinitesimal en teoría corresponde a una flexión minúscula en el mundo real y al consiguiente deterioro de la estructura.

Un grafo rígido es una incrustación de un grafo en un espacio euclidiano que es estructuralmente rígido. ^[1] Es decir, un grafo es rígido si la estructura formada al reemplazar las aristas por varillas rígidas y los vértices por bisagras flexibles es rígida. Un grafo que no es rígido se llama flexible . Más formalmente, una incrustación de grafo es flexible si los vértices se pueden mover continuamente, preservando las distancias entre vértices adyacentes, con el resultado de que las distancias entre algunos vértices no adyacentes se alteran. ^[2] La última condición descarta congruencias euclidianas como la traslación y la rotación simples.

También es posible considerar problemas de rigidez para grafos en los que algunas aristas representan elementos de compresión (capaces de estirarse hasta una longitud mayor, pero no de encogerse hasta una longitud menor) mientras que otras aristas representan elementos de tensión (capaces de encogerse pero no de estirarse). Un grafo rígido con aristas de estos tipos forma un modelo matemático de una estructura de tensegridad .

El problema fundamental es cómo predecir la rigidez de una estructura mediante análisis teórico, sin necesidad de construirla. Entre los resultados clave en este ámbito se encuentran los siguientes:

• En cualquier dimensión, la rigidez de los vínculos de varilla y bisagra se describe mediante un matroide . Las bases del matroide de rigidez bidimensional (los gráficos mínimamente rígidos en el plano) son los gráficos de Laman .
• El teorema de Cauchy establece que un poliedro convexo tridimensional construido con placas rígidas para sus caras, conectadas por bisagras a lo largo de sus bordes, forma una estructura rígida.
• Los poliedros flexibles , poliedros no convexos que no son rígidos, fueron construidos por Raoul Bricard , Robert Connelly y otros. La conjetura de Fuelle , ahora demostrada, establece que todo movimiento continuo de un poliedro flexible conserva su volumen .
• En el problema de arriostramiento de la cuadrícula , donde el marco que se debe hacer rígido es una cuadrícula cuadrada con diagonales agregadas como arriostramiento transversal , la rigidez de la estructura se puede analizar traduciéndola a un problema sobre la conectividad de un gráfico bipartito subyacente . ^{[3] [4]}

Sin embargo, en muchas otras situaciones sencillas todavía no siempre se sabe cómo analizar matemáticamente la rigidez de una estructura, a pesar de la existencia de una considerable teoría matemática.

Uno de los fundadores de la teoría matemática de la rigidez estructural fue el físico James Clerk Maxwell . A finales del siglo XX se produjo un florecimiento de la teoría matemática de la rigidez, que continúa en el siglo XXI.

"[U]na teoría del equilibrio y de las deflexiones de los armazones sometidos a la acción de fuerzas actúa sobre la dureza de la calidad... en los casos en que el armazón... se refuerza con piezas de conexión adicionales... en los casos de tres dimensiones, por el método regular de ecuaciones de fuerzas, cada punto tendría tres ecuaciones para determinar su equilibrio, de modo que se obtendrían 3 s ecuaciones entre e cantidades desconocidas, si s es el número de puntos y e el número de conexiones[sic]. Sin embargo, hay seis ecuaciones de equilibrio del sistema que deben ser cumplidas necesariamente por las fuerzas, debido a la igualdad de acción y reacción en cada pieza. Por lo tanto, si e  = 3 s  − 6, el efecto de cualquier fuerza eterna será definido al producir tensiones o presiones en las diferentes piezas; pero si e  > 3 s  − 6, estas fuerzas serán indeterminadas...." ^[5]

• Criterio de Chebychev-Grübler-Kutzbach
• Contando con marcos de referencia
• Teorema de universalidad de Kempe

• Alfakih, Abdo Y. (2007), "Sobre la rigidez dimensional de estructuras de barras y uniones", Discrete Applied Mathematics , 155 (10): 1244–1253, doi : 10.1016/j.dam.2006.11.011 , MR  2332317.
• Connelly, Robert (1980), "La rigidez de ciertos marcos cableados y la rigidez de segundo orden de superficies convexas trianguladas arbitrariamente", Advances in Mathematics , 37 (3): 272–299, doi : 10.1016/0001-8708(80)90037-7 , MR  0591730.
• Crapo, Henry (1979), "Rigidez estructural", Topología estructural (1): 26–45, 73, hdl : 2099/521 , MR  0621627.
• Maxwell, JC (1864), "Sobre figuras recíprocas y diagramas de fuerzas", Philosophical Magazine , 4.ª serie, 27 (182): 250–261, doi :10.1080/14786446408643663.
• Rybnikov, Konstantin; Zaslavsky, Thomas (2005), "Criterios para el equilibrio en gráficos de ganancia abeliana, con aplicaciones a la geometría lineal por partes", Geometría discreta y computacional , 34 (2): 251–268, arXiv : math/0210052 , doi :10.1007/s00454-005-1170-6, MR  2155721, S2CID  14391276.
• Whiteley, Walter (1988), "La unión de matroides y la rigidez de los marcos", SIAM Journal on Discrete Mathematics , 1 (2): 237–255, doi :10.1137/0401025, MR  0941354