Resistencia de los materiales

El campo de la resistencia de los materiales (también llamado mecánica de materiales ) se refiere típicamente a varios métodos de cálculo de tensiones y deformaciones en elementos estructurales, como vigas, columnas y ejes. Los métodos empleados para predecir la respuesta de una estructura bajo carga y su susceptibilidad a varios modos de falla tienen en cuenta las propiedades de los materiales, como su límite elástico , resistencia última , módulo de Young y coeficiente de Poisson . Además, se consideran las propiedades macroscópicas del elemento mecánico (propiedades geométricas) como su longitud, ancho, espesor, restricciones de contorno y cambios abruptos en la geometría como agujeros.

La teoría comenzó con la consideración del comportamiento de miembros unidimensionales y bidimensionales de estructuras, cuyos estados de tensión pueden aproximarse como bidimensionales, y luego se generalizó a tres dimensiones para desarrollar una teoría más completa del comportamiento elástico y plástico de los materiales. Un importante pionero fundador en mecánica de materiales fue Stephen Timoshenko .

En la mecánica de materiales, la resistencia de un material es su capacidad para soportar una carga aplicada sin fallar ni deformarse plásticamente . El campo de la resistencia de los materiales se ocupa de las fuerzas y deformaciones que resultan de su acción sobre un material. Una carga aplicada a un elemento mecánico inducirá fuerzas internas dentro del elemento llamadas tensiones cuando esas fuerzas se expresan en base a una unidad. Las tensiones que actúan sobre el material provocan la deformación del material de varias maneras, incluida la rotura completa. La deformación del material se denomina deformación cuando esas deformaciones también se colocan en base a una unidad.

Para evaluar la capacidad de carga de un elemento mecánico, es necesario calcular las tensiones y deformaciones que se generan en él. Para ello, es necesario realizar una descripción completa de la geometría del elemento, sus restricciones, las cargas aplicadas al elemento y las propiedades del material del que está compuesto. Las cargas aplicadas pueden ser axiales (de tracción o compresión) o rotacionales (de esfuerzo cortante). Con una descripción completa de la carga y la geometría del elemento, es posible calcular el estado de tensión y deformación en cualquier punto del elemento. Una vez que se conoce el estado de tensión y deformación del elemento, es posible calcular la resistencia (capacidad de carga) de dicho elemento, sus deformaciones (cualidades de rigidez) y su estabilidad (capacidad de mantener su configuración original).

Las tensiones calculadas pueden entonces compararse con alguna medida de la resistencia del elemento, como su límite elástico o resistencia máxima. La deflexión calculada del elemento puede compararse con criterios de deflexión que se basan en el uso del elemento. La carga de pandeo calculada del elemento puede compararse con la carga aplicada. La rigidez calculada y la distribución de masa del elemento pueden utilizarse para calcular la respuesta dinámica del elemento y luego compararse con el entorno acústico en el que se utilizará.

La resistencia del material se refiere al punto en la curva de esfuerzo-deformación de ingeniería (límite de fluencia) más allá del cual el material experimenta deformaciones que no se revertirán por completo al retirar la carga y, como resultado, el elemento tendrá una deflexión permanente. La resistencia última del material se refiere al valor máximo de esfuerzo alcanzado. La resistencia a la fractura es el valor de esfuerzo en la fractura (el último valor de esfuerzo registrado).

• Cargas transversales : fuerzas aplicadas perpendicularmente al eje longitudinal de un elemento. Las cargas transversales hacen que el elemento se doble y se deforme respecto de su posición original, con tensiones internas de tracción y compresión que acompañan el cambio de curvatura del elemento. ^[1] Las cargas transversales también inducen fuerzas de corte que causan deformación por corte del material y aumentan la deflexión transversal del elemento.
• Carga axial: las fuerzas aplicadas son colineales con el eje longitudinal del elemento y hacen que el elemento se estire o se acorte. ^[2]
• Carga de torsión : Acción de torsión causada por un par de pares de fuerzas iguales y opuestamente dirigidas aplicadas externamente que actúan sobre planos paralelos o por un solo par externo aplicado a un miembro que tiene un extremo fijo contra la rotación.

La tensión uniaxial se expresa por

${\displaystyle \sigma ={\frac {F}{A}},}$

donde F es la fuerza que actúa sobre un área A. ^[3] El área puede ser el área no deformada o el área deformada, dependiendo de si lo que interesa es la tensión de ingeniería o la tensión verdadera.

• La tensión de compresión (o tensión de compresión ) es el estado de tensión causado por una carga aplicada que actúa para reducir la longitud del material ( elemento de compresión ) a lo largo del eje de la carga aplicada; es, en otras palabras, un estado de tensión que causa un aplastamiento del material. Un caso simple de compresión es la compresión uniaxial inducida por la acción de fuerzas opuestas de empuje. La resistencia a la compresión de los materiales es generalmente mayor que su resistencia a la tracción. Sin embargo, las estructuras cargadas en compresión están sujetas a modos de falla adicionales, como el pandeo , que dependen de la geometría del elemento.
• La tensión de tracción es el estado de tensión causado por una carga aplicada que tiende a alargar el material a lo largo del eje de la carga aplicada, en otras palabras, la tensión causada por la tracción del material. La resistencia de las estructuras de igual área de sección transversal cargadas en tensión es independiente de la forma de la sección transversal. Los materiales cargados en tensión son susceptibles a concentraciones de tensión, como defectos de material o cambios abruptos en la geometría. Sin embargo, los materiales que presentan un comportamiento dúctil (muchos metales, por ejemplo) pueden tolerar algunos defectos, mientras que los materiales frágiles (como la cerámica y algunos aceros) pueden fallar muy por debajo de su resistencia máxima.
• La tensión cortante es el estado de tensión causado por la energía combinada de un par de fuerzas opuestas que actúan a lo largo de líneas de acción paralelas a través del material, en otras palabras, la tensión causada por las caras del material que se deslizan una respecto de la otra. Un ejemplo es cortar papel con tijeras ^[4] o las tensiones debidas a una carga de torsión.

La resistencia de los materiales se puede expresar en varios parámetros de tensión mecánica . El término resistencia de los materiales se utiliza cuando se hace referencia a los parámetros de tensión mecánica . Se trata de magnitudes físicas con dimensiones homogéneas a la presión y la fuerza por unidad de superficie . Por tanto, la unidad de medida tradicional para la resistencia es el MPa en el Sistema Internacional de Unidades y el psi entre las unidades habituales de los Estados Unidos . Los parámetros de resistencia incluyen: resistencia a la fluencia, resistencia a la tracción, resistencia a la fatiga, resistencia al agrietamiento y otros parámetros. ^{[ cita requerida ]}

• El límite elástico es la tensión más baja que produce una deformación permanente en un material. En algunos materiales, como las aleaciones de aluminio , el punto de fluencia es difícil de identificar, por lo que se suele definir como la tensión necesaria para provocar una deformación plástica del 0,2 %. Esto se denomina tensión de prueba del 0,2 %. ^[5]

• La resistencia a la compresión es un estado límite de tensión de compresión que conduce a la falla de un material en forma de falla dúctil (fluencia teórica infinita) o falla frágil (ruptura como resultado de la propagación de grietas o deslizamiento a lo largo de un plano débil – ver resistencia al corte ).
• La resistencia a la tracción o resistencia máxima a la tracción es un estado límite de tensión de tracción que conduce a una falla por tracción en forma de falla dúctil (límite de fluencia como primera etapa de esa falla, cierto endurecimiento en la segunda etapa y rotura después de una posible formación de "cuello") o falla frágil (rotura repentina en dos o más piezas en un estado de baja tensión). La resistencia a la tracción se puede expresar como tensión verdadera o tensión de ingeniería, pero la tensión de ingeniería es la más comúnmente utilizada.
• La resistencia a la fatiga es una medida más compleja de la resistencia de un material que considera varios episodios de carga en el período de servicio de un objeto, ^[6] y suele ser más difícil de evaluar que las medidas de resistencia estática. La resistencia a la fatiga se cita aquí como un rango simple (). En el caso de la carga cíclica, se puede expresar adecuadamente como una amplitud, generalmente a una tensión media cero, junto con el número de ciclos hasta la falla bajo esa condición de tensión.${\displaystyle \Delta \sigma =\sigma _{\mathrm {max} }-\sigma _{\mathrm {min} }}$

• La resistencia al impacto es la capacidad del material para soportar una carga aplicada repentinamente y se expresa en términos de energía. A menudo se mide con la prueba de resistencia al impacto Izod o la prueba de impacto Charpy , que miden la energía de impacto necesaria para fracturar una muestra. El volumen, el módulo de elasticidad , la distribución de fuerzas y el límite elástico afectan la resistencia al impacto de un material. Para que un material u objeto tenga una alta resistencia al impacto, las tensiones deben distribuirse uniformemente por todo el objeto. También debe tener un gran volumen con un bajo módulo de elasticidad y un alto límite elástico del material. ^[7]

• La deformación del material es el cambio en la geometría que se crea cuando se aplica tensión (como resultado de fuerzas aplicadas, campos gravitacionales, aceleraciones, expansión térmica, etc.). La deformación se expresa mediante el campo de desplazamiento del material. ^[8]
• La deformación , o deformación reducida , es un término matemático que expresa la tendencia del cambio de deformación entre el campo material. La deformación es la deformación por unidad de longitud. ^[9] En el caso de carga uniaxial, el desplazamiento de una muestra (por ejemplo, un elemento de barra) conduce a un cálculo de la deformación expresada como el cociente del desplazamiento y la longitud original de la muestra. Para campos de desplazamiento 3D se expresa como derivadas de funciones de desplazamiento en términos de un tensor de segundo orden (con 6 elementos independientes).
• La deflexión es un término para describir la magnitud a la que se desplaza un elemento estructural cuando está sujeto a una carga aplicada. ^[10]

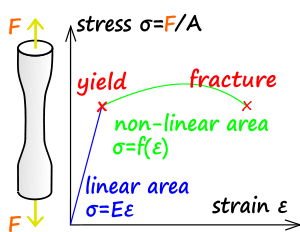
• La elasticidad es la capacidad de un material de volver a su forma anterior después de liberar la tensión. En muchos materiales, la relación entre la tensión aplicada es directamente proporcional a la deformación resultante (hasta un cierto límite), y un gráfico que representa esas dos cantidades es una línea recta.

La pendiente de esta línea se conoce como módulo de Young o "módulo de elasticidad". El módulo de elasticidad se puede utilizar para determinar la relación tensión-deformación en la parte elástica lineal de la curva tensión-deformación. La región elástica lineal está por debajo del punto de fluencia o, si no se identifica fácilmente un punto de fluencia en la gráfica de tensión-deformación, se define como entre 0 y 0,2 % de deformación y se define como la región de deformación en la que no se produce fluencia (deformación permanente). ^[11]

• La plasticidad o deformación plástica es lo opuesto a la deformación elástica y se define como una deformación irrecuperable. La deformación plástica se mantiene después de la liberación de la tensión aplicada. La mayoría de los materiales de la categoría elástico-lineal suelen ser capaces de deformarse plásticamente. Los materiales frágiles, como la cerámica, no experimentan ninguna deformación plástica y se fracturarán bajo una deformación relativamente baja, mientras que los materiales dúctiles, como los metálicos, el plomo o los polímeros, se deformarán plásticamente mucho más antes de iniciarse la fractura.

Considere la diferencia entre una zanahoria y un chicle masticado. La zanahoria se estirará muy poco antes de romperse. El chicle masticado, por otro lado, se deformará plásticamente enormemente antes de romperse definitivamente.

La resistencia máxima es un atributo relacionado con un material, en lugar de solo una muestra específica hecha del material, y como tal se cita como la fuerza por unidad de área de sección transversal (N/m2 ⁾ . La resistencia máxima es la tensión máxima que un material puede soportar antes de romperse o debilitarse. ^[12] Por ejemplo, la resistencia máxima a la tracción (UTS) del acero AISI 1018 es 440 MPa . En unidades imperiales, la unidad de tensión se da como lbf/in2 ^o libras -fuerza por pulgada cuadrada . Esta unidad a menudo se abrevia como psi . Mil psi se abrevia ksi .

Un factor de seguridad es un criterio de diseño que un componente o estructura de ingeniería debe alcanzar. , donde FS: el factor de seguridad, Rf la tensión aplicada y F: tensión máxima admisible (psi o MPa) ^[13]${\displaystyle FS=F/f}$

El margen de seguridad es el método común para los criterios de diseño. Se define como MS = P _u /P − 1.

Por ejemplo, para lograr un factor de seguridad de 4, la tensión admisible en un componente de acero AISI 1018 se puede calcular como = 440/4 = 110 MPa, o = 110×10 ⁶ N/m ² . Estas tensiones admisibles también se conocen como "tensiones de diseño" o "tensiones de trabajo".${\displaystyle F=UTS/FS}$${\estilo de visualización F}$

Las tensiones de diseño que se han determinado a partir de los valores de los puntos de fluencia o de límite de fluencia de los materiales dan resultados seguros y fiables sólo para el caso de carga estática. Muchas piezas de máquinas fallan cuando se someten a cargas no constantes y que varían continuamente, aunque las tensiones desarrolladas estén por debajo del punto de fluencia. Estas fallas se denominan fallas por fatiga. La falla se produce por una fractura que parece frágil con poca o ninguna evidencia visible de fluencia. Sin embargo, cuando la tensión se mantiene por debajo de la "tensión de fatiga" o la "tensión límite de resistencia", la pieza resistirá indefinidamente. Una tensión puramente inversa o cíclica es aquella que alterna entre tensiones pico positivas y negativas iguales durante cada ciclo de operación. En una tensión puramente cíclica, la tensión media es cero. Cuando una pieza se somete a una tensión cíclica, también conocida como rango de tensión (Sr), se ha observado que la falla de la pieza se produce después de una serie de inversiones de tensión (N) incluso si la magnitud del rango de tensión está por debajo de la resistencia a la fluencia del material. Generalmente, cuanto mayor sea el rango de tensión, menor será el número de reversiones necesarias para que se produzca una falla.

Existen cuatro teorías de falla: teoría de esfuerzo cortante máximo, teoría de esfuerzo normal máximo, teoría de energía de deformación máxima y teoría de energía de distorsión máxima (criterio de falla de von Mises). De estas cuatro teorías de falla, la teoría de esfuerzo normal máximo solo es aplicable para materiales frágiles, y las tres teorías restantes son aplicables para materiales dúctiles. De las últimas tres, la teoría de energía de distorsión proporciona los resultados más precisos en la mayoría de las condiciones de estrés. La teoría de energía de deformación necesita el valor del coeficiente de Poisson del material de la pieza, que a menudo no está fácilmente disponible. La teoría de esfuerzo cortante máximo es conservadora. Para esfuerzos normales unidireccionales simples, todas las teorías son equivalentes, lo que significa que todas las teorías darán el mismo resultado.

• La teoría del esfuerzo cortante máximo postula que se producirá una falla si la magnitud del esfuerzo cortante máximo en la pieza excede la resistencia al corte del material determinada a partir de pruebas uniaxiales.
• La teoría de la tensión normal máxima postula que se producirá una falla si la tensión normal máxima en la pieza excede la tensión de tracción máxima del material, determinada a partir de pruebas uniaxiales. Esta teoría se aplica únicamente a materiales frágiles. La tensión de tracción máxima debe ser menor o igual a la tensión de tracción máxima dividida por el factor de seguridad. La magnitud de la tensión de compresión máxima debe ser menor que la tensión de compresión máxima dividida por el factor de seguridad.
• La teoría de la energía de deformación máxima postula que la falla ocurrirá cuando la energía de deformación por unidad de volumen debido a las tensiones aplicadas en una pieza sea igual a la energía de deformación por unidad de volumen en el punto de rendimiento en la prueba uniaxial.
• Teoría de la energía de máxima distorsión , también conocida como teoría de la energía de máxima distorsión de falla o teoría de von Mises-Hencky . Esta teoría postula que la falla ocurrirá cuando la energía de distorsión por unidad de volumen debido a las tensiones aplicadas en una pieza sea igual a la energía de distorsión por unidad de volumen en el punto de fluencia en pruebas uniaxiales. La energía elástica total debido a la deformación se puede dividir en dos partes: una parte causa un cambio en el volumen y la otra parte causa un cambio en la forma. La energía de distorsión es la cantidad de energía que se necesita para cambiar la forma.
• La mecánica de fracturas fue establecida por Alan Arnold Griffith y George Rankine Irwin . Esta importante teoría también se conoce como conversión numérica de la tenacidad del material en caso de existencia de grietas.

La resistencia de un material depende de su microestructura . Los procesos de ingeniería a los que se somete un material pueden alterar esta microestructura. La variedad de mecanismos de fortalecimiento que alteran la resistencia de un material incluye endurecimiento por trabajo , fortalecimiento por solución sólida , endurecimiento por precipitación y fortalecimiento del límite de grano y se pueden explicar cuantitativa y cualitativamente. Los mecanismos de fortalecimiento están acompañados de la advertencia de que algunas otras propiedades mecánicas del material pueden degenerar en un intento de hacer que el material sea más fuerte. Por ejemplo, en el fortalecimiento del límite de grano, aunque el límite elástico se maximiza con la disminución del tamaño de grano, en última instancia, los tamaños de grano muy pequeños hacen que el material sea frágil. En general, el límite elástico de un material es un indicador adecuado de la resistencia mecánica del material. Considerado en conjunto con el hecho de que el límite elástico es el parámetro que predice la deformación plástica en el material, uno puede tomar decisiones informadas sobre cómo aumentar la resistencia de un material dependiendo de sus propiedades microestructurales y el efecto final deseado. La resistencia se expresa en términos de los valores límite de la tensión de compresión , la tensión de tracción y las tensiones de corte que causarían falla. Los efectos de la carga dinámica son probablemente la consideración práctica más importante de la teoría de la elasticidad, especialmente el problema de la fatiga . La carga repetida a menudo inicia grietas, que crecen hasta que se produce la falla en la resistencia residual correspondiente de la estructura. Las grietas siempre comienzan en concentraciones de tensión , especialmente cambios en la sección transversal del producto o defectos en la fabricación, cerca de agujeros y esquinas a niveles de tensión nominal mucho más bajos que los citados para la resistencia del material.

• Teorías del fracaso
• Estudios de casos de falla estructural