Relación entre área de superficie y volumen
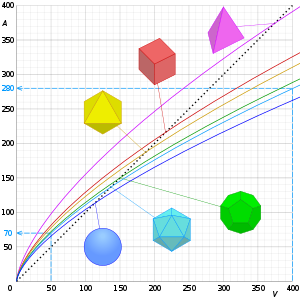
Área de superficie por unidad de volumen
Gráficas del área superficial, A , en función del volumen, V, de los sólidos platónicos y de una esfera, que muestran que el área superficial disminuye para las formas más redondeadas, y la relación entre el área superficial y el volumen disminuye con el aumento del volumen. Las intersecciones con las líneas discontinuas muestran que cuando el volumen aumenta 8 (2³) veces, el área superficial aumenta 4 (2²) veces.

La relación área-volumen o relación superficie-volumen (denotada como SA:V , SA/V o sa/vol ) es la relación entre el área de superficie y el volumen de un objeto o colección de objetos.

SA:V es un concepto importante en ciencia e ingeniería. Se utiliza para explicar la relación entre estructura y función en procesos que ocurren a través de la superficie y el volumen. Buenos ejemplos de tales procesos son los procesos regidos por la ecuación del calor , [1] es decir, difusión y transferencia de calor por conducción térmica . [2] SA:V se utiliza para explicar la difusión de moléculas pequeñas, como oxígeno y dióxido de carbono entre el aire, la sangre y las células, [3] la pérdida de agua por parte de los animales, [4] la morfogénesis bacteriana, [5] la termorregulación de los organismos , [6] el diseño de tejido óseo artificial, [7] pulmones artificiales [8] y muchas más estructuras biológicas y biotecnológicas. Para más ejemplos, consulte Glazier. [9]

La relación entre SA:V y la velocidad de difusión o conducción de calor se explica desde la perspectiva del flujo y la superficie, centrándose en la superficie de un cuerpo como el lugar donde tiene lugar la difusión o conducción de calor, es decir, cuanto mayor sea la SA:V, mayor será el área de superficie por unidad de volumen a través del cual el material puede difundirse, por lo tanto, la difusión o conducción de calor será más rápida. Una explicación similar aparece en la literatura: "Un tamaño pequeño implica una gran relación de área de superficie a volumen, lo que ayuda a maximizar la absorción de nutrientes a través de la membrana plasmática", [10] y en otros lugares. [9] [11] [12]

Para un volumen dado, el objeto con la menor área superficial (y por lo tanto con la menor SA:V) es una pelota , consecuencia de la desigualdad isoperimétrica en 3 dimensiones . Por el contrario, los objetos con puntas en ángulos agudos tendrán una superficie muy grande para un volumen dado.

Para esferas sólidas

Gráfico de la relación área superficial:volumen (SA:V) de una bola tridimensional, que muestra que la relación disminuye inversamente a medida que aumenta el radio de la bola.

Una esfera o bola sólida es un objeto tridimensional , siendo la figura sólida delimitada por una esfera . (En geometría, el término esfera se refiere propiamente solo a la superficie, por lo que una esfera carece de volumen en este contexto).

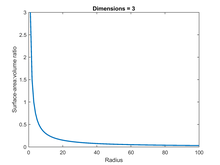
Para una bola tridimensional ordinaria, la SA:V se puede calcular utilizando las ecuaciones estándar para la superficie y el volumen, que son, respectivamente, y . Para el caso unitario en el que r = 1, la SA:V es, por tanto, 3. Para el caso general, SA:V es igual a 3/ r , en una relación inversa con el radio: si el radio se duplica, la SA:V se reduce a la mitad (véase la figura). S A = 4 π a 2 {\displaystyle SA=4\pi {r^{2}}} V = ( 4 / 3 ) π a 3 {\displaystyle V=(4/3)\pi {r^{3}}}

Paranorte-bolas dimensionales

Las bolas existen en cualquier dimensión y se denominan genéricamente n -bolas o hiperbolas , donde n es el número de dimensiones. El mismo razonamiento se puede generalizar a las n-bolas utilizando las ecuaciones generales para el volumen y el área de superficie, que son:

V = a norte π norte / 2 Γ ( 1 + norte / 2 ) {\displaystyle V={\frac {r^{n}\pi ^{n/2}}{\Gamma (1+n/2)}}}
S A = norte a norte − 1 π norte / 2 Γ ( 1 + norte / 2 ) {\displaystyle SA={\frac {nr^{n-1}\pi ^{n/2}}{\Gamma (1+{n/2})}}}

Por lo tanto, la relación es igual a . Por lo tanto, la misma relación lineal entre área y volumen se cumple para cualquier número de dimensiones (ver figura): duplicar el radio siempre reduce a la mitad la relación. S A / V = norte a − 1 {\displaystyle SA/V=nr^{-1}}

Dimensiones y unidades

La relación entre la superficie y el volumen tiene una dimensión física inversa a la longitud (L −1 ) y, por lo tanto, se expresa en unidades de metro inverso (m -1 ) o sus múltiplos y submúltiplos unitarios prefijados . A modo de ejemplo, un cubo con lados de 1  cm de longitud tendrá una superficie de 6 cm 2 y un volumen de 1 cm 3 . La relación entre la superficie y el volumen de este cubo es, por tanto,

SA:V = 6   centímetro 2 1   centímetro 3 = 6   centímetro − 1 {\displaystyle {\mbox{SA:V}}={\frac {6~{\mbox{cm}}^{2}}{1~{\mbox{cm}}^{3}}}=6~ {\mbox{cm}}^{-1}} .

Para una forma dada, SA:V es inversamente proporcional al tamaño. Un cubo de 2 cm de lado tiene una relación de 3 cm −1 , la mitad de la de un cubo de 1 cm de lado. Por el contrario, para conservar SA:V a medida que aumenta el tamaño es necesario cambiar a una forma menos compacta .

Aplicaciones

Química física

Los materiales con una alta relación área superficial / volumen (por ejemplo, diámetro muy pequeño, muy porosos o no compactos ) reaccionan a velocidades mucho más rápidas que los materiales monolíticos, porque hay más superficie disponible para reaccionar. Un ejemplo es el polvo de grano: si bien el grano no suele ser inflamable, el polvo de grano es explosivo . La sal finamente molida se disuelve mucho más rápidamente que la sal gruesa.

Una alta relación entre área superficial y volumen proporciona una potente "fuerza impulsora" para acelerar los procesos termodinámicos que minimizan la energía libre .

Biología

Las células que recubren el intestino delgado aumentan la superficie sobre la que pueden absorber nutrientes con una alfombra de microvellosidades en forma de penacho .

La relación entre la superficie y el volumen de las células y los organismos tiene un enorme impacto en su biología , incluida su fisiología y comportamiento . Por ejemplo, muchos microorganismos acuáticos han aumentado su superficie para aumentar su resistencia en el agua. Esto reduce su velocidad de hundimiento y les permite permanecer cerca de la superficie con un menor gasto de energía. [ cita requerida ]

Una mayor relación entre superficie y volumen también implica una mayor exposición al medio ambiente. Los apéndices finamente ramificados de los animales filtradores, como el krill, proporcionan una gran superficie para filtrar el agua en busca de alimento. [13]

Los órganos individuales como el pulmón tienen numerosas ramificaciones internas que aumentan el área de superficie; en el caso del pulmón, la gran superficie favorece el intercambio de gases, llevando oxígeno a la sangre y liberando dióxido de carbono de la sangre. [14] [15] De manera similar, el intestino delgado tiene una superficie interna finamente arrugada, lo que permite que el cuerpo absorba los nutrientes de manera eficiente. [16]

Las células pueden alcanzar una alta relación área superficial/volumen con una superficie elaboradamente contorneada, como las microvellosidades que recubren el intestino delgado . [17]

El aumento de la superficie también puede provocar problemas biológicos. Un mayor contacto con el medio ambiente a través de la superficie de una célula o un órgano (en relación con su volumen) aumenta la pérdida de agua y sustancias disueltas. Las relaciones elevadas entre superficie y volumen también plantean problemas de control de temperatura en entornos desfavorables. [ cita requerida ]

La relación superficie-volumen de organismos de diferentes tamaños también conduce a algunas reglas biológicas como la regla de Allen , la regla de Bergmann [18] [19] [20] y la gigantotermia . [21]

Propagación del fuego

En el contexto de los incendios forestales , la relación entre la superficie de un combustible sólido y su volumen es una medida importante. El comportamiento de propagación del fuego se correlaciona con frecuencia con la relación entre la superficie y el volumen del combustible (por ejemplo, hojas y ramas). Cuanto mayor sea su valor, más rápido responde una partícula a los cambios en las condiciones ambientales, como la temperatura o la humedad. Los valores más altos también se correlacionan con tiempos de ignición del combustible más cortos y, por lo tanto, con tasas de propagación del fuego más rápidas.

Enfriamiento planetario

Un cuerpo de material helado o rocoso en el espacio exterior puede, si puede acumular y retener suficiente calor, desarrollar un interior diferenciado y alterar su superficie mediante actividad volcánica o tectónica. El tiempo durante el cual un cuerpo planetario puede mantener una actividad que altere su superficie depende de lo bien que retenga el calor, y esto está determinado por su relación área-volumen. En el caso de Vesta (r=263 km), la relación es tan alta que los astrónomos se sorprendieron al descubrir que sí se diferenciaba y tenía una breve actividad volcánica. La luna , Mercurio y Marte tienen radios de unos miles de kilómetros; los tres retuvieron el calor lo suficientemente bien como para ser completamente diferenciados, aunque después de mil millones de años aproximadamente se volvieron demasiado fríos para mostrar algo más que una actividad volcánica muy localizada e infrecuente. Sin embargo, en abril de 2019, la NASA anunció la detección de un "martemoto" medido el 6 de abril de 2019 por el módulo de aterrizaje InSight de la NASA. [22] Venus y la Tierra (r>6.000 km) tienen relaciones superficie-volumen suficientemente bajas (aproximadamente la mitad de la de Marte y mucho más bajas que todos los demás cuerpos rocosos conocidos) como para que su pérdida de calor sea mínima. [23]

Ejemplos matemáticos

FormaImagen
Longitud característica a {\estilo de visualización a} 		Relación SA/VRelación SA/V por
unidad de volumen
Tetraedroborde 6 6 a ≈ 14.697 a {\displaystyle {\frac {6{\sqrt {6}}}{a}}\approx {\frac {14.697}{a}}} 7.21
Cuboborde 6 a {\displaystyle {\frac {6}{a}}} 6
Octaedroborde 3 6 a ≈ 7.348 a {\displaystyle {\frac {3{\sqrt {6}}}{a}}\approx {\frac {7.348}{a}}} 5.72
Dodecaedroborde 12 25 + 10 5 ( 15 + 7 5 ) a ≈ 2.694 a {\displaystyle {\frac {12{\sqrt {25+10{\sqrt {5}}}}}{(15+7{\sqrt {5}})a}}\approx {\frac {2.694}{a}}} 5.31
Cápsula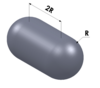radio (R) 12 5 a {\displaystyle {\frac {12}{5a}}} 5.251
Icosaedroborde 12 3 ( 3 + 5 ) a ≈ 3.970 a {\displaystyle {\frac {12{\sqrt {3}}}{(3+{\sqrt {5}})a}}\approx {\frac {3.970}{a}}} 5.148
Esferaradio 3 a {\displaystyle {\frac {3}{a}}} 4.83598
Ejemplos de cubos de diferentes tamaños
Lado del
cubo		Lado 2Área de una
sola cara		6 × lado 2Área del
cubo entero
(6 caras)		Lado 3VolumenRelación entre
el área de superficie
y el volumen
22×246×2×2242×2×283:1
44×4166×4×4964×4×4643:2
66×6366×6×62166×6×62163:3
88×8646×8×83848×8×85123:4
1212×121446×12×1286412×12×121.7283:6
2020×204006×20×202.40020×20×208.0003:10
5050×502.5006×50×5015.00050×50×50125.0003:25
1.0001.000 × 1.0001.000.0006×1.000×1.0006.000.0001.000 × 1.000 × 1.0001.000.000.0003:500

Véase también

Referencias

  • Schmidt-Nielsen, Knut (1984). Escalado: ¿por qué es tan importante el tamaño de los animales? . Nueva York, NY: Cambridge University Press. ISBN 978-0-521-26657-4.OCLC 10697247  .
  • Vogel, Steven (1988). Los mecanismos de la vida: el mundo físico de los animales y las plantas . Princeton, NJ: Princeton University Press. ISBN 978-0-691-08504-3.OCLC 18070616  .
Específico
  1. ^ Planinšič, Gorazd; Vollmer, Michael (20 de febrero de 2008). "La relación superficie-volumen en física térmica: desde la física del cubo de queso hasta el metabolismo animal". Revista Europea de Física . 29 (2): 369–384. Bibcode :2008EJPh...29..369P. doi :10.1088/0143-0807/29/2/017. S2CID  55488270 . Consultado el 9 de julio de 2021 .
  2. ^ Planinšič, Gorazd (2008). "La relación superficie-volumen en física térmica: desde la física del cubito de queso hasta el metabolismo animal". Revista Europea de Física, Sociedad Europea de Física, Más información . 29 (2): 369–384. Bibcode :2008EJPh...29..369P. doi :10.1088/0143-0807/29/2/017. S2CID  55488270.
  3. ^ Williams, Peter; Warwick, Roger; Dyson, Mary; Bannister, Lawrence H. (2005). Anatomía de Gray (39.ª ed.). Churchill Livingstone. págs. 1278–1282.
  4. ^ Jeremy M., Howard; Hannah-Beth, Griffis; Westendorf, Rachel; Williams, Jason B. (2019). "La influencia del tamaño y los factores abióticos en la pérdida de agua cutánea". Avances en la educación en fisiología . 44 (3): 387–393. doi : 10.1152/advan.00152.2019 . PMID  32628526.
  5. ^ Harris, Leigh K.; Theriot, Julie A. (2018). "Relación entre área de superficie y volumen: una variable natural para la morfogénesis bacteriana". Tendencias en microbiología . 26 (10): 815–832. doi :10.1016/j.tim.2018.04.008. PMC 6150810 . PMID  29843923. 
  6. ^ Louw, Gideon N. (1993). Ecología fisiológica animal . Longman Pub Group.
  7. ^ Nguyen, Thanh Danh; Olufemi E., Kadri; Vassilios I., Sikavitsas; Voronov, Roman S. (2019). "Los andamios con una alta relación superficie-volumen y cultivados bajo perfusión de flujo rápido dan como resultado un suministro óptimo de O2 a las células en tejidos óseos artificiales". Applied Sciences . 9 (11): 2381. doi : 10.3390/app9112381 .
  8. ^ J. K, Lee; HH, Kung; LF, Mockros (2008). "Tecnologías de microcanales para pulmones artificiales: (1) Teoría". Revista ASAIO . 54 (4): 372–382. doi : 10.1097/MAT.0b013e31817ed9e1 . PMID  18645354. S2CID  19505655.
  9. ^ ab Glazier, Douglas S. (2010). "Una explicación unificadora para la diversa escala metabólica en animales y plantas". Biological Reviews . 85 (1): 111–138. doi :10.1111/j.1469-185X.2009.00095.x. PMID  19895606. S2CID  28572410.
  10. ^ Alberts, Bruce (2002). "La diversidad de genomas y el árbol de la vida". Biología molecular de la célula, 4.ª edición. Nueva York: Garland Science. ISBN 0-8153-3218-1. ISBN 0-8153-4072-9 . 
  11. ^ Adam, John (1 de enero de 2020). "¿Cuál es su índice de esfericidad? Racionalización del área de superficie y el volumen". Profesor de matemáticas de Virginia . 46 (2).
  12. ^ Okie, Jordan G. (marzo de 2013). "Modelos generales para los espectros de estrategias de escalamiento de área de superficie de células y organismos: fractalidad, disimilitud geométrica e internalización". The American Naturalist . 181 (3): 421–439. doi :10.1086/669150. ISSN  1537-5323. PMID  23448890. S2CID  23434720.
  13. ^ Kils, U.: Natación y alimentación del krill antártico, Euphausia superba: algunos aspectos energéticos y dinámicos excepcionales: algunos detalles morfológicos únicos . En Berichte zur Polarforschung , Instituto Alfred Wegener de Investigación Polar y Marina , número especial 4 (1983): "Sobre la biología del krill Euphausia superba ", Actas del seminario e informe del Grupo de ecología del krill, editor SB Schnack, 130-155 e imagen de la página del título.
  14. ^ Tortora, Gerard J.; Anagnostakos, Nicholas P. (1987). Principios de anatomía y fisiología (quinta edición). Nueva York: Harper & Row, Publishers. págs. 556–582. ISBN 978-0-06-350729-6.
  15. ^ Williams, Peter L; Warwick, Roger; Dyson, Mary; Bannister, Lawrence H. (1989). Anatomía de Gray (37.ª ed.). Edimburgo: Churchill Livingstone. págs. 1278-1282. ISBN 0443-041776.
  16. ^ Romer, Alfred Sherwood; Parsons, Thomas S. (1977). El cuerpo de los vertebrados . Filadelfia, Pensilvania: Holt-Saunders International. págs. 349–353. ISBN. 978-0-03-910284-5.
  17. ^ Krause J. William (julio de 2005). Histología humana esencial de Krause para estudiantes de medicina. Universal-Publishers. pp. 37–. ISBN 978-1-58112-468-2. Consultado el 25 de noviembre de 2010 .
  18. ^ Meiri, S.; Dayan, T. (2003-03-20). "Sobre la validez de la regla de Bergmann". Journal of Biogeography . 30 (3): 331–351. Bibcode :2003JBiog..30..331M. doi :10.1046/j.1365-2699.2003.00837.x. S2CID  11954818.
  19. ^ Ashton, Kyle G.; Tracy, Mark C.; Queiroz, Alan de (octubre de 2000). "¿Es válida la regla de Bergmann para los mamíferos?". The American Naturalist . 156 (4): 390–415. doi :10.1086/303400. JSTOR  10.1086/303400. PMID  29592141. S2CID  205983729.
  20. ^ Millien, Virginie; Lyons, S. Kathleen; Olson, Link; et al. (23 de mayo de 2006). "Variación ecotípica en el contexto del cambio climático global: reconsideración de las reglas". Ecology Letters . 9 (7): 853–869. Bibcode :2006EcolL...9..853M. doi :10.1111/j.1461-0248.2006.00928.x. PMID  16796576.
  21. ^ Fitzpatrick, Katie (2005). "Gigantotermia". Davidson College . Archivado desde el original el 2012-06-30 . Consultado el 2011-12-21 .
  22. ^ "¡Terremoto en Marte! El módulo de aterrizaje InSight de la NASA siente su primer temblor en un planeta rojo". Space.com . 23 de abril de 2019.
  23. ^ "Copia archivada" (PDF) . Archivado desde el original (PDF) el 2018-06-13 . Consultado el 2018-08-22 .{{cite web}}: CS1 maint: copia archivada como título ( enlace )
  • Tamaños de los organismos: la relación superficie/volumen Archivado 2017-08-14 en Wayback Machine
  • Grupo Nacional de Coordinación de Incendios Forestales: Relación entre superficie y volumen
  • El enlace anterior no funciona, las referencias están en este documento, PDF

Lectura adicional

  • Sobre el tamaño adecuado, JBS Haldane Archivado el 22 de agosto de 2011 en Wayback Machine.
Obtenido de "https://es.wikipedia.org/w/index.php?title=Relación_superficie-volumen&oldid=1215129832"