Modelado de sólidos
Conjunto de principios para modelar geometría sólida

La geometría en el modelado de sólidos se describe completamente en el espacio 3D; los objetos pueden verse desde cualquier ángulo.

El modelado de sólidos (o modelado de sólidos ) es un conjunto consistente de principios para el modelado matemático y computacional de formas tridimensionales (sólidos) . El modelado de sólidos se distingue dentro de las áreas más amplias relacionadas con el modelado geométrico y los gráficos por computadora , como el modelado 3D , por su énfasis en la fidelidad física. [1] Juntos, los principios del modelado geométrico y sólido forman la base del diseño asistido por computadora en 3D y, en general, respaldan la creación, el intercambio, la visualización, la animación, la interrogación y la anotación de modelos digitales de objetos físicos.

Descripción general

El uso de técnicas de modelado de sólidos permite el proceso de automatización de varios cálculos de ingeniería difíciles que se llevan a cabo como parte del proceso de diseño. La simulación, planificación y verificación de procesos como el mecanizado y el ensamblaje fueron uno de los principales catalizadores para el desarrollo del modelado de sólidos. Más recientemente, la gama de aplicaciones de fabricación admitidas se ha ampliado en gran medida para incluir la fabricación de chapa metálica , el moldeo por inyección , la soldadura , el enrutamiento de tuberías , etc. Más allá de la fabricación tradicional, las técnicas de modelado de sólidos sirven como base para la creación rápida de prototipos , el archivo de datos digitales y la ingeniería inversa mediante la reconstrucción de sólidos a partir de puntos muestreados en objetos físicos, el análisis mecánico utilizando elementos finitos , la planificación del movimiento y la verificación de la trayectoria NC, el análisis cinemático y dinámico de mecanismos , etc. Un problema central en todas estas aplicaciones es la capacidad de representar y manipular eficazmente la geometría tridimensional de una manera que sea coherente con el comportamiento físico de los artefactos reales. La investigación y el desarrollo del modelado de sólidos han abordado eficazmente muchos de estos problemas y siguen siendo un foco central de la ingeniería asistida por computadora .

Fundamentos matemáticos

El concepto de modelado de sólidos tal como se practica hoy en día se basa en la necesidad específica de integridad de la información en los sistemas de modelado geométrico mecánico, en el sentido de que cualquier modelo informático debe admitir todas las consultas geométricas que se puedan hacer a su objeto físico correspondiente. El requisito reconoce implícitamente la posibilidad de varias representaciones informáticas del mismo objeto físico siempre que dos de esas representaciones sean consistentes. Es imposible verificar computacionalmente la integridad de la información de una representación a menos que la noción de un objeto físico se defina en términos de propiedades matemáticas computables e independientemente de cualquier representación particular. Tal razonamiento condujo al desarrollo del paradigma de modelado que ha dado forma al campo del modelado de sólidos tal como lo conocemos hoy. [2]

Todos los componentes fabricados tienen un tamaño finito y límites que se comportan bien , por lo que inicialmente el enfoque se centró en modelar matemáticamente piezas rígidas hechas de material isotrópico homogéneo que se pudiera agregar o quitar. Estas propiedades postuladas se pueden traducir en propiedades de regiones , subconjuntos del espacio euclidiano tridimensional . Los dos enfoques comunes para definir la "solidez" se basan en la topología de conjuntos de puntos y la topología algebraica respectivamente. Ambos modelos especifican cómo se pueden construir sólidos a partir de piezas o celdas simples.

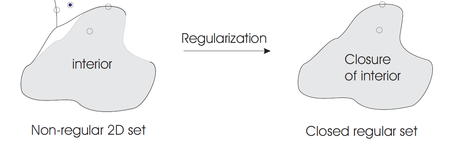
Regularización de un conjunto 2D tomando el cierre de su interior

Según el modelo de solidez de conjunto de puntos continuos, todos los puntos de cualquier X ⊂ ℝ 3 pueden clasificarse según sus vecindades con respecto a X como puntos interiores , exteriores o límites . Suponiendo que ℝ 3 está dotado de la métrica euclidiana típica , una vecindad de un punto p ∈ X toma la forma de una bola abierta . Para que X se considere sólido, cada vecindad de cualquier p ∈ X debe ser consistentemente tridimensional; los puntos con vecindades de menor dimensión indican una falta de solidez. La homogeneidad dimensional de las vecindades está garantizada para la clase de conjuntos regulares cerrados , definidos como conjuntos iguales a la clausura de su interior. Cualquier X ⊂ ℝ 3 puede convertirse en un conjunto regular cerrado o "regularizado" tomando la clausura de su interior, y por lo tanto el espacio de modelado de sólidos se define matemáticamente como el espacio de subconjuntos regulares cerrados de ℝ 3 (por el teorema de Heine-Borel se implica que todos los sólidos son conjuntos compactos ). Además, se requiere que los sólidos sean cerrados bajo las operaciones booleanas de unión, intersección y diferencia de conjuntos (para garantizar la solidez después de la adición y eliminación de material). La aplicación de las operaciones booleanas estándar a conjuntos regulares cerrados puede no producir un conjunto regular cerrado, pero este problema se puede resolver regularizando el resultado de la aplicación de las operaciones booleanas estándar. [3] Las operaciones de conjunto regularizadas se denotan ∪ ∗ , ∩ ∗ y − ∗ .

La caracterización combinatoria de un conjunto X ⊂ ℝ 3 como un sólido implica representar a X como un complejo de celdas orientables de modo que las celdas proporcionen direcciones espaciales finitas para puntos en un continuo que de otro modo sería innumerable. [1] La clase de subconjuntos acotados semianalíticos del espacio euclidiano está cerrada bajo operaciones booleanas (estándar y regularizadas) y exhibe la propiedad adicional de que cada conjunto semianalítico puede estratificarse en una colección de celdas disjuntas de dimensiones 0,1,2,3. Una triangulación de un conjunto semianalítico en una colección de puntos, segmentos de línea , caras triangulares y elementos tetraédricos es un ejemplo de una estratificación que se usa comúnmente. El modelo combinatorio de solidez se resume entonces diciendo que además de ser subconjuntos acotados semianalíticos, los sólidos son poliedros topológicos tridimensionales , específicamente variedades orientables tridimensionales con borde. [4] En particular, esto implica que la característica de Euler del límite combinatorio [5] del poliedro es 2. El modelo combinatorio de variedad de solidez también garantiza que el límite de un sólido separa el espacio en exactamente dos componentes como consecuencia del teorema de Jordan-Brouwer , eliminando así los conjuntos con vecindarios no múltiples que se consideran imposibles de fabricar.

Los modelos de sólidos de conjunto puntual y combinatorio son completamente consistentes entre sí, se pueden usar indistintamente, basándose en propiedades continuas o combinatorias según sea necesario, y se pueden extender a n dimensiones. La propiedad clave que facilita esta consistencia es que la clase de subconjuntos regulares cerrados de ℝ n coincide precisamente con poliedros topológicos homogéneamente n -dimensionales. Por lo tanto, cada sólido n -dimensional puede representarse inequívocamente por su límite y el límite tiene la estructura combinatoria de un poliedro n-1 -dimensional que tiene vecindarios homogéneos n-1 -dimensionales.

Esquemas de representación de sólidos

Basándose en las propiedades matemáticas asumidas, cualquier esquema de representación de sólidos es un método para capturar información sobre la clase de subconjuntos semianalíticos del espacio euclidiano. Esto significa que todas las representaciones son formas diferentes de organizar los mismos datos geométricos y topológicos en forma de una estructura de datos . Todos los esquemas de representación se organizan en términos de un número finito de operaciones sobre un conjunto de primitivas. Por lo tanto, el espacio de modelado de cualquier representación particular es finito, y cualquier esquema de representación individual puede no ser completamente suficiente para representar todos los tipos de sólidos. Por ejemplo, los sólidos definidos a través de combinaciones de operaciones booleanas regularizadas no necesariamente se pueden representar como el barrido de una primitiva que se mueve según una trayectoria espacial, excepto en casos muy simples. Esto obliga a los sistemas de modelado geométrico modernos a mantener varios esquemas de representación de sólidos y también a facilitar la conversión eficiente entre esquemas de representación.

A continuación se muestra una lista de técnicas utilizadas para crear o representar modelos sólidos. [4] El software de modelado moderno puede utilizar una combinación de estos esquemas para representar un sólido.

Instanciación primitiva

Este esquema se basa en la noción de familias de objetos, cada miembro de una familia se distingue de los demás por unos pocos parámetros. Cada familia de objetos se denomina primitiva genérica y los objetos individuales dentro de una familia se denominan instancias primitivas . Por ejemplo, una familia de tornillos es una primitiva genérica y un único tornillo especificado por un conjunto particular de parámetros es una instancia primitiva. La característica distintiva de los esquemas de instanciación puramente parametrizados es la falta de medios para combinar instancias para crear nuevas estructuras que representen objetos nuevos y más complejos. El otro inconveniente principal de este esquema es la dificultad de escribir algoritmos para calcular las propiedades de los sólidos representados. Se debe incorporar una cantidad considerable de información específica de la familia en los algoritmos y, por lo tanto, cada primitiva genérica debe tratarse como un caso especial, lo que no permite un tratamiento general uniforme.

Enumeración de ocupación espacial

Este esquema es esencialmente una lista de celdas espaciales ocupadas por el sólido. Las celdas, también llamadas vóxeles , son cubos de un tamaño fijo y están dispuestas en una cuadrícula espacial fija (también son posibles otras disposiciones poliédricas, pero los cubos son los más simples). Cada celda puede representarse mediante las coordenadas de un único punto, como el centroide de la celda. Por lo general, se impone un orden de escaneo específico y el conjunto ordenado de coordenadas correspondiente se denomina matriz espacial . Las matrices espaciales son representaciones sólidas inequívocas y únicas, pero son demasiado verbosas para su uso como representaciones "maestras" o de definición. Sin embargo, pueden representar aproximaciones burdas de partes y pueden usarse para mejorar el rendimiento de los algoritmos geométricos, especialmente cuando se usan junto con otras representaciones como la geometría sólida constructiva .

Descomposición celular

Este esquema se deriva de las descripciones combinatorias (topológicas algebraicas) de sólidos detalladas anteriormente. Un sólido puede representarse mediante su descomposición en varias celdas. Los esquemas de enumeración de ocupación espacial son un caso particular de descomposiciones de celdas donde todas las celdas son cúbicas y se encuentran en una cuadrícula regular. Las descomposiciones de celdas proporcionan formas convenientes para calcular ciertas propiedades topológicas de los sólidos, como su conectividad (número de piezas) y género (número de agujeros). Las descomposiciones de celdas en forma de triangulaciones son las representaciones utilizadas en elementos finitos 3D para la solución numérica de ecuaciones diferenciales parciales. Otras descomposiciones de celdas, como una estratificación regular de Whitney o descomposiciones de Morse, pueden usarse para aplicaciones en la planificación del movimiento de robots. [6]

Modelado de malla de superficie

De manera similar a la representación de límites, se representa la superficie del objeto. Sin embargo, en lugar de estructuras de datos complejas y NURBS, se utiliza una malla de superficie simple de vértices y aristas. Las mallas de superficie pueden ser estructuradas (como las mallas triangulares en archivos STL o las mallas cuádruples con anillos horizontales y verticales de cuadriláteros) o mallas no estructuradas con triángulos agrupados aleatoriamente y polígonos de nivel superior.

Geometría sólida constructiva

La geometría sólida constructiva (CSG) es una familia de esquemas para representar sólidos rígidos como construcciones booleanas o combinaciones de primitivas a través de las operaciones de conjuntos regularizados discutidas anteriormente. La CSG y las representaciones de contorno son actualmente los esquemas de representación más importantes para sólidos. Las representaciones CSG toman la forma de árboles binarios ordenados donde los nodos no terminales representan transformaciones rígidas ( isometrías que preservan la orientación ) u operaciones de conjuntos regularizados. Los nodos terminales son hojas primitivas que representan conjuntos regulares cerrados. La semántica de las representaciones CSG es clara. Cada subárbol representa un conjunto resultante de aplicar las transformaciones indicadas/operaciones de conjuntos regularizados en el conjunto representado por las hojas primitivas del subárbol. Las representaciones CSG son particularmente útiles para capturar la intención del diseño en forma de características correspondientes a la adición o eliminación de material (protuberancias, agujeros, bolsillos, etc.). Las propiedades atractivas de CSG incluyen concisión, validez garantizada de los sólidos, propiedades algebraicas booleanas computacionalmente convenientes y control natural de la forma de un sólido en términos de parámetros de alto nivel que definen las primitivas del sólido y sus posiciones y orientaciones. La estructura de datos relativamente simple y los algoritmos recursivos elegantes [7] han contribuido aún más a la popularidad de CSG.

General

La noción básica incorporada en los esquemas de barrido es simple. Un conjunto que se mueve a través del espacio puede trazar o barrer un volumen (un sólido) que puede representarse por el conjunto en movimiento y su trayectoria. Tal representación es importante en el contexto de aplicaciones como la detección del material retirado de una cortadora a medida que se mueve a lo largo de una trayectoria específica, el cálculo de la interferencia dinámica de dos sólidos que experimentan un movimiento relativo, la planificación del movimiento e incluso en aplicaciones de gráficos de computadora como el seguimiento de los movimientos de un pincel movido sobre un lienzo. La mayoría de los sistemas CAD comerciales proporcionan una funcionalidad (limitada) para construir sólidos barridos principalmente en forma de una sección transversal bidimensional que se mueve en una trayectoria espacial transversal a la sección. Sin embargo, la investigación actual ha mostrado varias aproximaciones de formas tridimensionales que se mueven a través de un parámetro, e incluso movimientos multiparamétricos.

Representación implícita

Un método muy general para definir un conjunto de puntos X es especificar un predicado que pueda evaluarse en cualquier punto del espacio. En otras palabras, X se define implícitamente como que consta de todos los puntos que satisfacen la condición especificada por el predicado. La forma más simple de un predicado es la condición sobre el signo de una función de valor real que da como resultado la representación familiar de conjuntos mediante igualdades y desigualdades. Por ejemplo, si las condiciones , , y representan, respectivamente, un plano y dos semiespacios lineales abiertos . Se pueden definir primitivas funcionales más complejas mediante combinaciones booleanas de predicados más simples. Además, la teoría de funciones R permite conversiones de tales representaciones en una única desigualdad de función para cualquier conjunto semianalítico cerrado. Dicha representación se puede convertir en una representación de contorno utilizando algoritmos de poligonización, por ejemplo, el algoritmo de cubos en marcha . F = a incógnita + b y + do el + d {\displaystyle f=ax+by+cz+d} F ( pag ) = 0 {\displaystyle f(p)=0} F ( pag ) > 0 {\displaystyle f(p)>0} F ( pag ) < 0 {\displaystyle f(p)<0}

Modelado paramétrico y basado en características

Las características se definen como formas paramétricas asociadas con atributos tales como parámetros geométricos intrínsecos (longitud, ancho, profundidad, etc.), posición y orientación, tolerancias geométricas , propiedades del material y referencias a otras características. [8] Las características también proporcionan acceso a procesos de producción relacionados y modelos de recursos. Por lo tanto, las características tienen un nivel semántico más alto que los conjuntos regulares cerrados primitivos. En general, se espera que las características formen una base para vincular CAD con aplicaciones de fabricación posteriores y también para organizar bases de datos para la reutilización de datos de diseño. El modelado basado en características paramétricas se combina con frecuencia con geometría sólida binaria constructiva (CSG) para describir completamente sistemas de objetos complejos en ingeniería.

Historia de los modeladores de sólidos

El desarrollo histórico de los modeladores de sólidos debe verse en el contexto de toda la historia del CAD , siendo los hitos clave el desarrollo del sistema de investigación BUILD seguido de su spin-off comercial Romulus que influyó en el desarrollo de Parasolid , ACIS y Solid Modeling Solutions . ASCON, uno de los primeros desarrolladores de CAD en la Comunidad de Estados Independientes (CEI), comenzó el desarrollo interno de su propio modelador de sólidos en la década de 1990. [9] En noviembre de 2012, la división matemática de ASCON se convirtió en una empresa separada y se denominó C3D Labs . Se le asignó la tarea de desarrollar el núcleo de modelado geométrico C3D como un producto independiente, el único núcleo de modelado 3D comercial de Rusia. [10] Otras contribuciones vinieron de Mäntylä, con su GWB y del proyecto GPM que contribuyó, entre otras cosas, con técnicas de modelado híbrido a principios de la década de 1980. Esto también es cuando se concibió el lenguaje de programación de modelado de sólidos PLaSM en la Universidad de Roma.

Diseño asistido por ordenador

El modelado de sólidos es sólo el requisito mínimo de las capacidades de un sistema CAD . Los modeladores de sólidos se han convertido en algo común en los departamentos de ingeniería en los últimos diez años [ ¿cuándo? ] debido a las computadoras más rápidas y los precios competitivos del software. El software de modelado de sólidos crea una representación virtual en 3D de los componentes para el diseño y análisis de máquinas. [11] Una interfaz gráfica de usuario típica incluye macros programables, atajos de teclado y manipulación dinámica del modelo. Se enfatiza la capacidad de reorientar dinámicamente el modelo, en 3-D sombreado en tiempo real, y ayuda al diseñador a mantener una imagen mental en 3-D.

Un modelo de pieza sólida generalmente consta de un grupo de características, que se agregan una a la vez, hasta que el modelo está completo. Los modelos sólidos de ingeniería se construyen principalmente con características basadas en bocetos; bocetos 2D que se desplazan a lo largo de una trayectoria para convertirse en 3D. Estos pueden ser cortes o extrusiones, por ejemplo. El trabajo de diseño de los componentes generalmente se realiza dentro del contexto de todo el producto utilizando métodos de modelado de ensamblajes . Un modelo de ensamblaje incorpora referencias a modelos de piezas individuales que componen el producto. [12]

Otro tipo de técnica de modelado es el "superficie" ( modelado de superficies de forma libre ). Aquí, las superficies se definen, se recortan, se fusionan y se rellenan para hacerlas sólidas. Las superficies se definen generalmente con curvas de referencia en el espacio y una variedad de comandos complejos. El modelado de superficies es más difícil, pero se aplica mejor a algunas técnicas de fabricación, como el moldeo por inyección. Los modelos sólidos para piezas moldeadas por inyección suelen tener características basadas tanto en superficies como en esbozos.

Se pueden crear dibujos de ingeniería de forma semiautomática y hacer referencia a los modelos sólidos.

Modelado paramétrico

El modelado paramétrico utiliza parámetros para definir un modelo (dimensiones, por ejemplo). Algunos ejemplos de parámetros son: dimensiones utilizadas para crear características del modelo, densidad del material, fórmulas para describir características de barrido, datos importados (que describen una superficie de referencia, por ejemplo). El parámetro se puede modificar más tarde y el modelo se actualizará para reflejar la modificación. Normalmente, existe una relación entre piezas, conjuntos y dibujos. Una pieza consta de varias características y un conjunto consta de varias piezas. Los dibujos se pueden realizar a partir de piezas o conjuntos.

Ejemplo: Se crea un eje extruyendo un círculo de 100 mm. Se ensambla un cubo al final del eje. Luego, el eje se modifica para que tenga una longitud de 200 mm (haga clic en el eje, seleccione la dimensión de longitud y modifíquela a 200). Cuando se actualice el modelo, el eje tendrá una longitud de 200 mm, el cubo se reubicará en el extremo del eje al que se ensambló y los planos de ingeniería y las propiedades de masa reflejarán todos los cambios automáticamente.

Las restricciones están relacionadas con los parámetros, pero son ligeramente diferentes . Las restricciones son relaciones entre entidades que forman una forma particular. Para una ventana, los lados pueden definirse como paralelos y de la misma longitud. El modelado paramétrico es obvio e intuitivo. Pero durante las primeras tres décadas de CAD, este no era el caso. La modificación significaba volver a dibujar o agregar un nuevo corte o protuberancia sobre los anteriores. Las dimensiones en los dibujos de ingeniería se creaban en lugar de mostrarse . El modelado paramétrico es muy poderoso, pero requiere más habilidad en la creación de modelos. Un modelo complicado para una pieza moldeada por inyección puede tener mil características, y modificar una característica temprana puede hacer que las características posteriores fallen. Los modelos paramétricos creados hábilmente son más fáciles de mantener y modificar. El modelado paramétrico también se presta a la reutilización de datos. Por ejemplo, una familia completa de tornillos de cabeza hueca puede estar contenida en un modelo.

Modelado de sólidos médicos

Los escáneres de tomografía axial computarizada y resonancia magnética modernos se pueden utilizar para crear modelos sólidos de las características internas del cuerpo, denominados modelos basados ​​en vóxeles , con imágenes generadas mediante renderización de volumen . Los escáneres ópticos 3D se pueden utilizar para crear nubes de puntos o modelos de malla poligonal de las características externas del cuerpo.

Usos del modelado de sólidos médicos;

Si el uso va más allá de la visualización de los datos escaneados, serán necesarios procesos como la segmentación de imágenes y el mallado basado en imágenes para generar una descripción geométrica precisa y realista de los datos escaneados.

Ingeniería

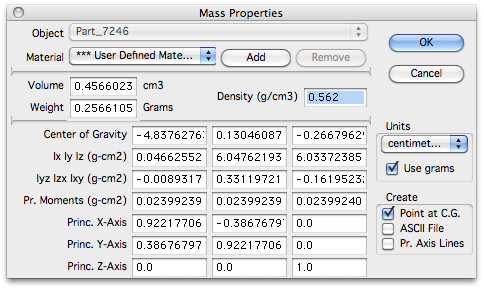
Ventana de propiedades que describe las propiedades de masa de un modelo en Cobalt
Ventana de propiedades de masa de un modelo en Cobalt

Debido a que los programas CAD que se ejecutan en las computadoras "entienden" la geometría real que comprende formas complejas, se pueden calcular rápidamente muchos atributos de/para un sólido 3D, como su centro de gravedad, volumen y masa. Por ejemplo, el cubo con bordes redondeados que se muestra en la parte superior de este artículo mide 8,4 mm de plano a plano. A pesar de sus muchos radios y la pirámide poco profunda en cada una de sus seis caras, sus propiedades se calculan fácilmente para el diseñador, como se muestra en la captura de pantalla de la derecha.

Véase también

Referencias

  1. ^ ab Shapiro, Vadim (2001). Modelado de sólidos. Elsevier . Consultado el 20 de abril de 2010 .
  2. ^ Requicha, AAG y Voelcker, H. (1983). "Modelado de sólidos: estado actual y direcciones de investigación". IEEE Computer Graphics and Applications . 3 (7). IEEE Computer Graphics: 25–37. doi :10.1109/MCG.1983.263271. S2CID  14462567.
  3. ^ Tilove, RB; Requicha, AAG (1980), "Cierre de operaciones booleanas sobre entidades geométricas", Computer-Aided Design , 12 (5): 219–220, doi :10.1016/0010-4485(80)90025-1
  4. ^ ab Requicha, AAG (1980). "Representaciones para sólidos rígidos: teoría, métodos y sistemas". ACM Computing Surveys . 12 (4): 437–464. doi :10.1145/356827.356833. S2CID  207568300.
  5. ^ Hatcher, A. (2002). Topología algebraica. Cambridge University Press . Consultado el 20 de abril de 2010 .
  6. ^ Canny, John F. (1987). La complejidad de la planificación del movimiento de robots. MIT press, premio de tesis doctoral ACM . Consultado el 20 de abril de 2010 .
  7. ^ Ziegler, M. (2004). "Operadores computables en conjuntos regulares". Mathematical Logic Quarterly . 50 (45). Wiley: 392–404. doi :10.1002/malq.200310107. S2CID  17579181.
  8. ^ Mantyla, M., Nau, D. y Shah, J. (1996). "Desafíos en la investigación de fabricación basada en características". Comunicaciones de la ACM . 39 (2): 77–85. doi : 10.1145/230798.230808 . S2CID  3340804.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  9. ^ Yares, Evan (abril de 2013). "CAD ruso". Design World . 8 (4). WTWH Media, LLC. ISSN  1941-7217. Archivado desde el original el 30 de enero de 2015.
  10. ^ Golovanov, Nikolay (2014). Modelado geométrico: las matemáticas de las formas . CreateSpace Independent Publishing Platform (24 de diciembre de 2014). pág. Contraportada. ISBN 978-1497473195.
  11. ^ LaCourse, Donald (1995). "2". Manual de modelado de sólidos . McGraw Hill. pág. 2.5. ISBN 978-0-07-035788-4.
  12. ^ LaCourse, Donald (1995). "11". Manual de modelado de sólidos . McGraw Hill. pág. 111.2. ISBN 978-0-07-035788-4.
  • Biblioteca sgCore C++/C#
  • La Asociación de Modelado Sólido
Retrieved from "https://en.wikipedia.org/w/index.php?title=Solid_modeling&oldid=1262925125#Mathematical_foundations"