Regresión hacia la media

En estadística , la regresión hacia la media (también llamada regresión a la media , reversión a la media y reversión a la mediocridad ) es el fenómeno donde si una muestra de una variable aleatoria es extrema , es probable que la siguiente muestra de la misma variable aleatoria esté más cerca de su media . ^{[2] [3] [4]} Además, cuando se muestrean muchas variables aleatorias y se seleccionan intencionalmente los resultados más extremos, se refiere al hecho de que (en muchos casos) una segunda muestra de estas variables seleccionadas dará como resultado resultados "menos extremos", más cercanos a la media inicial de todas las variables.

Matemáticamente, la fuerza de este efecto de "regresión" depende de si todas las variables aleatorias provienen de la misma distribución o si existen diferencias genuinas en las distribuciones subyacentes para cada variable aleatoria. En el primer caso, es estadísticamente probable que se produzca el efecto de "regresión", pero en el segundo caso, puede que se produzca con menos fuerza o que no se produzca en absoluto.

La regresión hacia la media es, por lo tanto, un concepto útil a tener en cuenta al diseñar cualquier experimento científico, análisis de datos o prueba que seleccione intencionalmente los eventos más extremos; indica que los controles de seguimiento pueden ser útiles para evitar sacar conclusiones falsas sobre estos eventos; pueden ser eventos extremos genuinos, una selección completamente sin sentido debido al ruido estadístico o una mezcla de los dos casos. ^[5]

Consideremos una clase de estudiantes que toman un examen de verdadero/falso de 100 ítems sobre una materia. Supongamos que todos los estudiantes eligen aleatoriamente en todas las preguntas. Entonces, la puntuación de cada estudiante sería una realización de una de un conjunto de variables aleatorias independientes e idénticamente distribuidas , con una media esperada de 50. Naturalmente, algunos estudiantes obtendrán una puntuación sustancialmente superior a 50 y otros sustancialmente inferior a 50 simplemente por casualidad. Si uno selecciona solo el 10% de los estudiantes con la puntuación más alta y les da un segundo examen en el que nuevamente eligen aleatoriamente en todos los ítems, se esperaría que la puntuación media fuera nuevamente cercana a 50. Por lo tanto, la media de estos estudiantes "regresaría" hasta la media de todos los estudiantes que tomaron el examen original. No importa la puntuación que obtenga un estudiante en el examen original, la mejor predicción de su puntuación en el segundo examen es 50.

Si la elección de las respuestas a las preguntas del examen no fuera aleatoria –es decir, si no hubiera habido suerte (buena o mala) o conjeturas aleatorias en las respuestas proporcionadas por los estudiantes– entonces se esperaría que todos los estudiantes obtuvieran el mismo puntaje en el segundo examen que el puntaje en el examen original, y no habría regresión hacia la media.

La mayoría de las situaciones realistas se encuentran entre estos dos extremos: por ejemplo, se podría considerar que las calificaciones de los exámenes son una combinación de habilidad y suerte . En este caso, el subconjunto de estudiantes que obtuvieron calificaciones superiores a la media estaría compuesto por aquellos que eran hábiles y no tuvieron especialmente mala suerte, junto con aquellos que no eran hábiles, pero tuvieron mucha suerte. En una nueva prueba de este subconjunto, los no hábiles tendrán pocas probabilidades de repetir su golpe de suerte, mientras que los hábiles tendrán una segunda oportunidad de tener mala suerte. Por lo tanto, es poco probable que aquellos que obtuvieron buenos resultados anteriormente obtengan tan buenos resultados en la segunda prueba, incluso si la original no se puede reproducir.

El siguiente es un ejemplo de este segundo tipo de regresión hacia la media. Una clase de estudiantes toma dos ediciones del mismo examen en dos días sucesivos. Con frecuencia se ha observado que los peores resultados en el primer día tenderán a mejorar sus calificaciones en el segundo día, y los mejores resultados en el primer día tenderán a obtener peores resultados en el segundo día. El fenómeno ocurre porque las calificaciones de los estudiantes están determinadas en parte por la capacidad subyacente y en parte por el azar. En el primer examen, algunos tendrán suerte y obtendrán una calificación superior a su capacidad, y otros tendrán mala suerte y obtendrán una calificación inferior a su capacidad. Algunos de los estudiantes afortunados en el primer examen tendrán suerte nuevamente en el segundo, pero más de ellos tendrán (para ellos) calificaciones promedio o por debajo de la media. Por lo tanto, un estudiante que tuvo suerte y superó su capacidad en el primer examen tiene más probabilidades de obtener una calificación peor en el segundo examen que una calificación mejor. De manera similar, los estudiantes que por mala suerte obtuvieron una calificación inferior a su capacidad en el primer examen tenderán a ver sus calificaciones aumentar en el segundo examen. Cuanto mayor sea la influencia de la suerte en la producción de un evento extremo, menos probable será que la suerte se repita en múltiples eventos.

Si tu equipo deportivo favorito ganó el campeonato el año pasado, ¿qué significa eso para sus posibilidades de ganar la próxima temporada? En la medida en que este resultado se deba a la habilidad (el equipo está en buenas condiciones, tiene un entrenador de primer nivel, etc.), su victoria indica que es más probable que vuelva a ganar el año que viene. Pero cuanto más se deba a la suerte (otros equipos envueltos en un escándalo de drogas, sorteo favorable, selecciones del draft que resultaron productivas, etc.), menos probable es que vuelva a ganar el año que viene. ^[6]

Si una organización empresarial tiene un trimestre altamente rentable, a pesar de que las razones subyacentes para su desempeño no han cambiado, es probable que su desempeño no sea tan bueno en el trimestre siguiente. ^[7]

Los jugadores de béisbol que batean bien en su temporada de novatos probablemente lo hagan peor en la segunda; la " caída del segundo año ". De manera similar, la regresión hacia la media es una explicación de la maldición de la portada de Sports Illustrated : los períodos de rendimiento excepcional que resultan en un artículo de portada probablemente sean seguidos por períodos de rendimiento más mediocre, dando la impresión de que aparecer en la portada causa el declive de un atleta. ^[8]

El concepto de regresión proviene de la genética y fue popularizado por Sir Francis Galton a finales del siglo XIX con la publicación de Regresión hacia la mediocridad en la estatura hereditaria . ^[9] Galton observó que las características extremas (por ejemplo, la altura) de los padres no se transmiten completamente a su descendencia. Más bien, las características de la descendencia regresan hacia un punto mediocre (un punto que desde entonces se ha identificado como la media). Al medir las alturas de cientos de personas, pudo cuantificar la regresión a la media y estimar el tamaño del efecto. Galton escribió que "la regresión promedio de la descendencia es una fracción constante de sus respectivas desviaciones medias parentales ". Esto significa que la diferencia entre un niño y sus padres para alguna característica es proporcional a la desviación de sus padres con respecto a las personas típicas de la población. Si sus padres son dos pulgadas más altos que el promedio de hombres y mujeres, entonces, en promedio, la descendencia será más baja que sus padres por un factor (que, hoy, llamaríamos uno menos el coeficiente de regresión ) multiplicado por dos pulgadas. Para la altura, Galton estimó que este coeficiente era aproximadamente 2/3: la altura de un individuo medirá alrededor de un punto medio que es dos tercios de la desviación de los padres con respecto al promedio de la población.

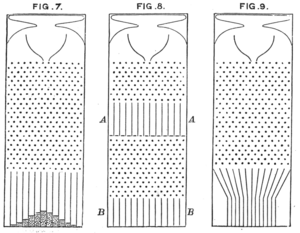
Galton también publicó estos resultados ^[10] utilizando el ejemplo más simple de bolitas que caen a través de un tablero de Galton para formar una distribución normal centrada directamente debajo de su punto de entrada. Estas bolitas podrían luego ser liberadas hacia abajo en una segunda galería correspondiente a una segunda medición. Galton luego hizo la pregunta inversa: "¿De dónde vinieron estas bolitas?"

La respuesta no fue “ en promedio, directamente arriba ” , sino “ en promedio, más hacia el medio ” , por la sencilla razón de que había más bolitas por encima, hacia el medio, que podían desviarse hacia la izquierda, que en el extremo izquierdo, que podían desviarse hacia la derecha, hacia adentro. ^[11]

Galton acuñó el término "regresión" para describir un hecho observable en la herencia de rasgos genéticos cuantitativos multifactoriales : a saber, que los rasgos de los descendientes de padres que se encuentran en los extremos de la distribución a menudo tienden a estar más cerca del centro, la media, de la distribución. Galton cuantificó esta tendencia y, al hacerlo, inventó el análisis de regresión lineal , sentando así las bases para gran parte de los modelos estadísticos modernos. Desde entonces, el término "regresión" se ha utilizado en otros contextos y puede ser utilizado por los estadísticos modernos para describir fenómenos como el sesgo de muestreo que tienen poco que ver con las observaciones originales de Galton en el campo de la genética.

La explicación de Galton para el fenómeno de regresión que observó en biología fue la siguiente: "Un niño hereda en parte de sus padres, en parte de sus antepasados. Hablando en general, cuanto más se remonta su genealogía, más numerosa y variada será su ascendencia, hasta que deje de diferir de cualquier muestra igualmente numerosa tomada al azar de la raza en general". ^[9] La afirmación de Galton requiere cierta aclaración a la luz del conocimiento de la genética: los niños reciben material genético de sus padres, pero la información hereditaria (por ejemplo, los valores de los rasgos heredados) de antepasados ​​anteriores puede transmitirse a través de sus padres (y puede no haberse expresado en sus padres). La media del rasgo puede no ser aleatoria y estar determinada por la presión de selección, pero la distribución de valores alrededor de la media refleja una distribución estadística normal.

El fenómeno genético poblacional estudiado por Galton es un caso especial de "regresión a la media"; el término se utiliza a menudo para describir muchos fenómenos estadísticos en los que los datos muestran una distribución normal alrededor de una media.

Esta sección necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables en esta sección. El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Regresión hacia la media» – noticias  · periódicos  · libros  · académico  · JSTOR ( noviembre de 2016 ) ( Aprenda cómo y cuándo eliminar este mensaje )

La regresión hacia la media es una consideración importante en el diseño de experimentos .

Tomemos un ejemplo hipotético de 1.000 personas de una edad similar a las que se les examinó y se les evaluó el riesgo de sufrir un ataque cardíaco. Se podrían utilizar estadísticas para medir el éxito de una intervención en las 50 personas que se clasificaron como de mayor riesgo, según lo medido por una prueba con un grado de incertidumbre. La intervención podría ser un cambio en la dieta, ejercicio o un tratamiento farmacológico. Incluso si las intervenciones no sirvieran de nada, se esperaría que el grupo de prueba mostrara una mejoría en su próximo examen físico, debido a la regresión hacia la media. La mejor manera de combatir este efecto es dividir al grupo aleatoriamente en un grupo de tratamiento que reciba el tratamiento y un grupo que no lo reciba. Entonces, el tratamiento se juzgaría eficaz solo si el grupo de tratamiento mejora más que el grupo no tratado.

Otra posibilidad es que se haga una prueba a un grupo de niños desfavorecidos para identificar a los que tienen más potencial para ir a la universidad. Se podría identificar al 1% superior y proporcionarle cursos especiales de enriquecimiento, tutoría, asesoramiento y computadoras. Incluso si el programa es eficaz, sus puntuaciones medias pueden ser inferiores cuando se repita la prueba un año después. Sin embargo, en estas circunstancias puede considerarse poco ético tener un grupo de control de niños desfavorecidos cuyas necesidades especiales se ignoran. Un cálculo matemático de la reducción puede ajustar este efecto, aunque no será tan fiable como el método del grupo de control (véase también el ejemplo de Stein ).

El efecto también puede aprovecharse para la inferencia y la estimación generales. El lugar más caluroso del país hoy tiene más probabilidades de ser más frío mañana que más caluroso, en comparación con hoy. El fondo de inversión con mejor rendimiento en los últimos tres años tiene más probabilidades de ver un descenso en el rendimiento relativo en lugar de una mejora en los próximos tres años. El actor de Hollywood más exitoso de este año probablemente tenga menos ingresos brutos, en lugar de más, por su próxima película. El jugador de béisbol con el promedio de bateo más alto a mitad de la temporada tiene más probabilidades de tener un promedio más bajo que un promedio más alto durante el resto de la temporada.

El concepto de regresión hacia la media puede usarse incorrectamente con mucha facilidad.

En el ejemplo de la prueba de los estudiantes que se muestra arriba, se supuso implícitamente que lo que se estaba midiendo no cambiaba entre las dos mediciones. Sin embargo, supongamos que el curso fuera de aprobado/reprobado y que los estudiantes debían obtener una puntuación superior a 70 en ambas pruebas para aprobar. En ese caso, los estudiantes que obtuvieron una puntuación inferior a 70 la primera vez no tendrían ningún incentivo para hacerlo bien y podrían obtener una puntuación peor en promedio la segunda vez. Los estudiantes que obtuvieron una puntuación ligeramente superior a 70, por otro lado, tendrían un fuerte incentivo para estudiar y concentrarse mientras hacían la prueba. En ese caso, uno podría ver un movimiento que se aleja de 70, puntuaciones inferiores a ese valor disminuyendo y puntuaciones superiores aumentando. Es posible que los cambios entre los momentos de la medición aumenten, compensen o inviertan la tendencia estadística a regresar hacia la media.

La regresión estadística hacia la media no es un fenómeno causal . Un estudiante con la peor puntuación en el examen el primer día no necesariamente aumentará sustancialmente su puntuación el segundo día debido al efecto. En promedio, los que obtienen las peores puntuaciones mejoran, pero eso es cierto solamente porque es más probable que hayan tenido mala suerte que suerte. En la medida en que una puntuación se determina aleatoriamente, o que una puntuación tiene una variación o error aleatorio, en lugar de estar determinada por la capacidad académica del estudiante o ser un "valor verdadero", el fenómeno tendrá un efecto. Un error clásico a este respecto se produjo en la educación. Se observó que los estudiantes que recibieron elogios por un buen trabajo obtuvieron peores resultados en la siguiente medición, y se observó que los estudiantes que fueron castigados por un mal trabajo obtuvieron mejores resultados en la siguiente medición. Los educadores decidieron dejar de elogiar y seguir castigando sobre esta base. ^[12] Tal decisión fue un error, porque la regresión hacia la media no se basa en la causa y el efecto, sino más bien en el error aleatorio en una distribución natural alrededor de una media.

Aunque las mediciones individuales extremas retroceden hacia la media, la segunda muestra de mediciones no estará más cerca de la media que la primera. Consideremos nuevamente a los estudiantes. Supongamos que la tendencia de los individuos extremos es retroceder un 10% del camino hacia la media de 80, por lo que se espera que un estudiante que obtuvo 100 puntos el primer día obtenga 98 puntos el segundo día, y que un estudiante que obtuvo 70 puntos el primer día obtenga 71 puntos el segundo día. Esas expectativas están más cerca de la media que las puntuaciones del primer día. Pero las puntuaciones del segundo día variarán en torno a sus expectativas; algunas serán más altas y otras serán más bajas. Para los individuos extremos, esperamos que la segunda puntuación esté más cerca de la media que la primera, pero para todos los individuos, esperamos que la distribución de distancias desde la media sea la misma en ambos conjuntos de mediciones.

En relación con el punto anterior, la regresión hacia la media funciona igualmente bien en ambas direcciones. Esperamos que el estudiante con la puntuación más alta en el segundo día haya tenido un peor rendimiento en el primer día. Y si comparamos al mejor estudiante del primer día con el mejor estudiante del segundo día, independientemente de si se trata del mismo individuo o no, no hay tendencia a la regresión hacia la media en ninguna de las dos direcciones. Esperamos que las mejores puntuaciones en ambos días estén igualmente alejadas de la media.

Muchos fenómenos tienden a atribuirse a causas equivocadas cuando no se tiene en cuenta la regresión a la media.

Un ejemplo extremo es el libro de Horace Secrist de 1933 El triunfo de la mediocridad en los negocios , en el que el profesor de estadística recogió montañas de datos para demostrar que las tasas de beneficio de las empresas competitivas tienden hacia la media a lo largo del tiempo. De hecho, no existe tal efecto; la variabilidad de las tasas de beneficio es casi constante a lo largo del tiempo. Secrist sólo había descrito la regresión común hacia la media. Un crítico exasperado, Harold Hotelling , comparó el libro con "probar la tabla de multiplicar organizando elefantes en filas y columnas, y luego haciendo lo mismo con numerosos otros tipos de animales". ^[13]

El cálculo e interpretación de las "puntuaciones de mejora" en las pruebas educativas estandarizadas en Massachusetts probablemente proporcione otro ejemplo de la falacia de la regresión. ^{[ cita requerida ]} En 1999, se dieron a las escuelas metas de mejora. Para cada escuela, el Departamento de Educación tabuló la diferencia en la puntuación media obtenida por los estudiantes en 1999 y en 2000. Se observó rápidamente que la mayoría de las escuelas con peores resultados habían cumplido sus metas, lo que el Departamento de Educación tomó como confirmación de la solidez de sus políticas. Sin embargo, también se observó que muchas de las supuestamente mejores escuelas de la Commonwealth, como la Brookline High School (con 18 finalistas de la Beca Nacional al Mérito) fueron declaradas fallidas. Como en muchos casos que involucran estadísticas y políticas públicas, la cuestión es debatida, pero las "puntuaciones de mejora" no se anunciaron en los años posteriores y los resultados parecen ser un caso de regresión a la media.

El psicólogo Daniel Kahneman , premio Nobel de Economía en 2002 , señaló que la regresión a la media podría explicar por qué los reproches parecen mejorar el rendimiento, mientras que los elogios parecen ser contraproducentes. ^[14]

Tuve la experiencia Eureka más satisfactoria de mi carrera mientras intentaba enseñar a los instructores de vuelo que el elogio es más eficaz que el castigo para fomentar el aprendizaje de habilidades. Cuando terminé mi entusiasta discurso, uno de los instructores más experimentados del público levantó la mano y pronunció su propio discurso breve, que comenzó reconociendo que el refuerzo positivo podría ser bueno para las aves, pero continuó negando que fuera óptimo para los cadetes de vuelo. Dijo: "En muchas ocasiones he elogiado a los cadetes de vuelo por la ejecución limpia de alguna maniobra acrobática y, en general, cuando lo intentan de nuevo, lo hacen peor. Por otro lado, a menudo les he gritado a los cadetes por una mala ejecución y, en general, lo hacen mejor la próxima vez. Así que, por favor, no nos digan que el refuerzo funciona y el castigo no, porque es lo contrario". Fue un momento de alegría, en el que comprendí una verdad importante sobre el mundo: como tendemos a recompensar a los demás cuando hacen bien las cosas y a castigarlos cuando las hacen mal, y como hay regresión a la media, es parte de la condición humana que se nos castigue estadísticamente por recompensar a los demás y se nos recompense por castigarlos. Inmediatamente organicé una demostración en la que cada participante arrojó dos monedas a un objetivo que tenía detrás de la espalda, sin ninguna retroalimentación. Medimos las distancias desde el objetivo y pudimos ver que los que habían hecho las cosas mejor la primera vez habían empeorado en su mayoría en el segundo intento, y viceversa. Pero sabía que esta demostración no desharía los efectos de la exposición de por vida a una contingencia perversa.

La falacia de regresión también se explica en El arte de pensar con claridad de Rolf Dobelli .

Las políticas de aplicación de la ley del Reino Unido han fomentado la ubicación visible de cámaras de velocidad fijas o móviles en los puntos negros de accidentes . Esta política se justificó por la percepción de que hay una reducción correspondiente en los accidentes de tráfico graves después de la instalación de una cámara. Sin embargo, los estadísticos han señalado que, aunque existe un beneficio neto en vidas salvadas, el hecho de no tener en cuenta los efectos de la regresión a la media da como resultado que se sobrestimen los efectos beneficiosos. ^{[15] [16] [17]}

Los analistas estadísticos reconocen desde hace tiempo el efecto de la regresión a la media en los deportes; incluso tienen un nombre especial para ello: la " caída del segundo año ". Por ejemplo, Carmelo Anthony, de los Denver Nuggets de la NBA , tuvo una temporada de novato sobresaliente en 2004. Fue tan sobresaliente que no se podía esperar que la repitiera: en 2005, los números de Anthony habían caído con respecto a su temporada de novato. Las razones para la "caída del segundo año" abundan, ya que los deportes dependen del ajuste y el contraajuste, pero la excelencia basada en la suerte como novato es una razón tan buena como cualquier otra. La regresión a la media en el rendimiento deportivo también puede explicar la aparente " maldición de la portada de Sports Illustrated " y la " maldición de Madden ". John Hollinger tiene un nombre alternativo para el fenómeno de la regresión a la media: la "regla de la casualidad" ^{[ cita requerida ]} , mientras que Bill James lo llama el "principio de plexiglás". ^{[ cita requerida ]}

Debido a que la tradición popular se ha centrado en la regresión hacia la media como una explicación del declive del rendimiento de los atletas de una temporada a la siguiente, por lo general se ha pasado por alto el hecho de que dicha regresión también puede explicar la mejora del rendimiento. Por ejemplo, si se observa el promedio de bateo de los jugadores de las Grandes Ligas de Béisbol en una temporada, aquellos cuyo promedio de bateo fue superior a la media de la liga tienden a retroceder hacia la media el año siguiente, mientras que aquellos cuyo promedio de bateo fue inferior a la media tienden a progresar hacia la media el año siguiente. ^[18]

La regresión hacia la media simplemente dice que, después de un evento aleatorio extremo, es probable que el próximo evento aleatorio sea menos extremo. En ningún sentido el evento futuro "compensa" o "equilibra" el evento anterior, aunque esto se supone en la falacia del jugador (y la variante de la ley de promedios ). De manera similar, la ley de los grandes números establece que, a largo plazo, el promedio tenderá hacia el valor esperado, pero no hace ninguna afirmación sobre los ensayos individuales. Por ejemplo, después de una racha de 10 caras en un lanzamiento de una moneda justa (un evento extremo raro), la regresión a la media establece que la próxima racha de caras probablemente será menor que 10, mientras que la ley de los grandes números establece que, a largo plazo, este evento probablemente se promediará, y la fracción promedio de caras tenderá a 1/2. Por el contrario, la falacia del jugador supone incorrectamente que la moneda ahora "está lista" para una racha de cruces para equilibrarse.

El efecto opuesto es la regresión hacia la cola, resultante de una distribución con densidad de probabilidad que no desaparece hacia el infinito. ^[19]

Esta es la definición de regresión hacia la media que sigue de cerca el uso original de Sir Francis Galton . ^[9]

Supongamos que hay n puntos de datos { y _i , x _i }, donde i  = 1, 2, ..., n . Queremos encontrar la ecuación de la línea de regresión , es decir, la línea recta

${\displaystyle y=\alpha +\beta x,\,}$

que proporcionaría un mejor ajuste para los puntos de datos. (Una línea recta puede no ser la curva de regresión adecuada para los puntos de datos dados). Aquí, lo mejor se entenderá como en el enfoque de mínimos cuadrados : una línea que minimice la suma de los residuos al cuadrado del modelo de regresión lineal. En otras palabras, los números α y β resuelven el siguiente problema de minimización:

Encuentra , donde${\displaystyle \min _{\alpha ,\,\beta }Q(\alpha ,\beta )}$${\displaystyle Q(\alpha ,\beta )=\suma _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\suma _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\ }$

Utilizando el cálculo se puede demostrar que los valores de α y β que minimizan la función objetivo Q son

${\displaystyle {\begin{aligned}&{\hat {\beta }}={\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}={\frac {{\overline {xy}}-{\bar {x}}{\bar {y}}}{{\overline {x^{2}}}-{\bar {x}}^{2}}}={\frac {\operatorname {Cov} [x,y]}{\operatorname {Var} [x]}}=r_{xy}{\frac {s_{y}}{s_{x}}},\\&{\hat {\alpha }}={\bar {y}}-{\hat {\beta }}\,{\bar {x}},\end{aligned}}}$

donde r _xy es el coeficiente de correlación muestral entre x e y , s _x es la desviación estándar de x y s _y es, en consecuencia, la desviación estándar de y . La barra horizontal sobre una variable significa el promedio muestral de esa variable. Por ejemplo:${\displaystyle {\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .}$

Sustituyendo las expresiones anteriores por y en se obtienen valores ajustados.${\displaystyle {\hat {\alpha }}}$${\displaystyle {\hat {\beta }}}$${\displaystyle y=\alpha +\beta x,\,}$

${\displaystyle {\hat {y}}={\hat {\alpha }}+{\hat {\beta }}x,\,}$

que produce

${\displaystyle {\frac {{\hat {y}}-{\bar {y}}}{s_{y}}}=r_{xy}{\frac {x-{\bar {x}}}{s_{x}}}}$

Esto muestra el papel que juega r _xy en la línea de regresión de puntos de datos estandarizados.

Si −1 <  r _xy  < 1, entonces decimos que los puntos de datos presentan regresión hacia la media. En otras palabras, si la regresión lineal es el modelo apropiado para un conjunto de puntos de datos cuyo coeficiente de correlación muestral no es perfecto, entonces hay regresión hacia la media. El valor estandarizado predicho (o ajustado) de y está más cerca de su media que el valor estandarizado de x de su media. ^{[ cita requerida ]}

Sean X ₁ , X ₂ variables aleatorias con distribuciones marginales idénticas con media μ . En esta formalización, se dice que la distribución bivariada de X ₁ y X ₂ exhibe regresión hacia la media si, para cada número c  >  μ , tenemos

μ  ≤ E[ X ₂  |  X ₁  =  c ] <  c ,

con las desigualdades inversas manteniéndose para c  <  μ . ^{[20] [21]}

La siguiente es una descripción informal de la definición anterior. Considere una población de widgets . Cada widget tiene dos números, X ₁ y X ₂ (digamos, su amplitud izquierda ( X ₁ ) y amplitud derecha ( X ₂ )). Suponga que las distribuciones de probabilidad de X ₁ y X ₂ en la población son idénticas, y que las medias de X ₁ y X ₂ son ambas μ . Ahora tomamos un widget aleatorio de la población y denotamos su valor X _{1 por} c . ( c puede ser mayor que, igual a o menor que μ .) Todavía no tenemos acceso al valor de X _{2 de este widget. Sea} d el valor esperado de X ₂ de este widget en particular. ( es decir, sea d el valor promedio de X ₂ de todos los widgets en la población con X ₁ = c .) Si la siguiente condición es verdadera:

Cualquiera que sea el valor de c , d se encuentra entre μ y c ( es decir, d está más cerca de μ que c ),

Entonces decimos que X ₁ y X ₂ muestran regresión hacia la media .

Esta definición concuerda estrechamente con el uso común actual, que evolucionó a partir del uso original de Galton, del término "regresión hacia la media". Es "restrictiva" en el sentido de que no todas las distribuciones bivariadas con distribuciones marginales idénticas presentan regresión hacia la media (según esta definición). ^[21]

Si un par ( X ,  Y ) de variables aleatorias sigue una distribución normal bivariada , entonces la media condicional E( Y | X ) es una función lineal de X . El coeficiente de correlación r entre X e Y , junto con las medias y varianzas marginales de X e Y , determina esta relación lineal:

${\displaystyle {\frac {E(Y\mid X)-E[Y]}{\sigma _{y}}}=r{\frac {X-E[X]}{\sigma _{x}}},}$

donde E[X] y E[Y] son ​​los valores esperados de X e Y , respectivamente, y σ _x y σ _y son las desviaciones estándar de X e Y , respectivamente.

Por lo tanto, el valor esperado condicional de Y , dado que X está t desviaciones estándar por encima de su media (y eso incluye el caso en que está por debajo de su media, cuando t  < 0), es rt desviaciones estándar por encima de la media de Y . Dado que | r | ≤ 1, Y no está más lejos de la media que X , medida en el número de desviaciones estándar. ^[22]

Por lo tanto, si 0 ≤  r  < 1, entonces ( X ,  Y ) muestra regresión hacia la media (según esta definición).

Samuels propuso la siguiente definición de reversión hacia la media como alternativa a la definición más restrictiva de regresión hacia la media anterior. ^[20]

Sean X ₁ , X ₂ variables aleatorias con distribuciones marginales idénticas con media μ . En esta formalización, se dice que la distribución bivariada de X ₁ y X _{2 exhibe} reversión hacia la media si, para cada número c , tenemos

μ  ≤ E[ X ₂  |  X ₁  >  c ] < E[ X ₁  |  X ₁  >  c ], y

μ  ≥ E[ X ₂  |  X ₁  <  c ] > E[ X ₁  |  X ₁  <  c ]

Esta definición es "general" en el sentido de que toda distribución bivariada con distribuciones marginales idénticas exhibe reversión hacia la media , siempre que se cumplan algunos criterios débiles (no degeneración y dependencia positiva débil como se describe en el artículo de Samuels ^[20] ).

Jeremy Siegel utiliza el término "retorno a la media" para describir una serie temporal financiera en la que " los retornos pueden ser muy inestables en el corto plazo pero muy estables en el largo plazo". Más cuantitativamente, es aquella en la que la desviación estándar de los retornos anuales promedio disminuye más rápido que la inversa del período de tenencia, lo que implica que el proceso no es un paseo aleatorio , sino que los períodos de retornos más bajos son seguidos sistemáticamente por períodos compensatorios de retornos más altos, como es el caso en muchos negocios estacionales, por ejemplo. ^[23]

• Principio de Hardy-Weinberg
• Validez interna
• Ley de los grandes números
• Martingala (teoría de la probabilidad)
• Dilución de regresión
• Sesgo de selección

• JM Bland y DG Altman (junio de 1994). "Notas estadísticas: regresión hacia la media". British Medical Journal . 308 (6942): 1499. doi :10.1136/bmj.308.6942.1499. PMC  2540330 . PMID  8019287.Artículo, incluyendo un diagrama de los datos originales de Galton.

• Edward J. Dudewicz y Satya N. Mishra (1988). "Sección 14.1: Estimación de parámetros de regresión; modelos lineales". Estadística matemática moderna . John Wiley & Sons . ISBN 978-0-471-81472-6.

• Francis Galton (1886). "Regresión hacia la mediocridad en la estatura hereditaria" (PDF) . Revista del Instituto Antropológico de Gran Bretaña e Irlanda . 15 : 246–263. doi :10.2307/2841583. JSTOR  2841583.

• Donald F. Morrison (1967). "Capítulo 3: Muestras de la población normal multivariante". Métodos estadísticos multivariantes . McGraw-Hill . ISBN 978-0-534-38778-5.

• Stephen M. Stigler (1999). "Capítulo 9". Estadísticas sobre la mesa . Harvard University Press .

• Myra L. Samuels (noviembre de 1991). "Reversión estadística hacia la media: más universal que la regresión hacia la media". The American Statistician . 45 (4): 344–346. doi :10.2307/2684474. JSTOR  2684474.
• Stephen Senn. Regresión: un nuevo modo para un viejo significado, The American Statistician , vol. 44, n.º 2 (mayo de 1990), págs. 181-183.
• Regresión hacia la media y el estudio del cambio, Psychological Bulletin
• Una explicación no matemática de la regresión hacia la media.
• Una simulación de regresión hacia la media.
• Amanda Wachsmuth, Leland Wilkinson, Gerard E. Dallal. La curva de Galton: una no linealidad no descubierta en los datos de regresión de estatura familiar de Galton y una explicación probable basada en los datos de estatura de Pearson y Lee (una mirada moderna al análisis de Galton).
• Puntuaciones de las pruebas estandarizadas de Massachusetts, interpretadas por un estadístico como un ejemplo de regresión: consulte la discusión en sci.stat.edu y su continuación.
• Gary Smith , ¡Qué suerte!: El sorprendente papel del azar en nuestra vida cotidiana, Nueva York: Overlook, Londres: Duckworth. ISBN 978-1-4683-1375-8 . 

• Medios relacionados con Regresión hacia la media en Wikimedia Commons