Detener el tiempo

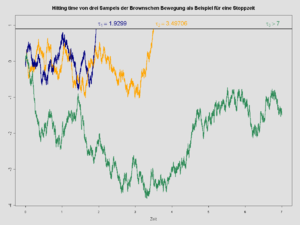
En teoría de la probabilidad , en particular en el estudio de los procesos estocásticos , un tiempo de detención (también tiempo de Markov , momento de Markov , tiempo de detención opcional o tiempo opcional ^[1] ) es un tipo específico de “tiempo aleatorio”: una variable aleatoria cuyo valor se interpreta como el momento en el que un proceso estocástico dado exhibe un cierto comportamiento de interés. Un tiempo de detención a menudo se define por una regla de detención , un mecanismo para decidir si continuar o detener un proceso sobre la base de la posición actual y los eventos pasados, y que casi siempre conducirá a una decisión de detenerse en un tiempo finito.

Los tiempos de parada se dan en la teoría de la decisión , y el teorema de parada opcional es un resultado importante en este contexto. Los tiempos de parada también se aplican con frecuencia en las demostraciones matemáticas para “domar el continuo del tiempo”, como lo expresó Chung en su libro (1982).

Sea una variable aleatoria, que se define en el espacio de probabilidad filtrado con valores en . Entonces se denomina tiempo de parada (con respecto a la filtración ), si se cumple la siguiente condición:${\estilo de visualización \tau}$ ${\displaystyle (\Omega ,{\mathcal {F}},({\mathcal {F}}_{n})_{n\in \mathbb {N} },P)}$${\displaystyle \mathbb {N} \cup \{+\infty \}}$${\estilo de visualización \tau}$ ${\displaystyle \mathbb {F} =(({\mathcal {F}}_{n})_{n\in \mathbb {N} }}$

${\displaystyle \{\tau =n\}\in {\mathcal {F}}_{n}}$a pesar de${\estilo de visualización n}$

Intuitivamente, esta condición significa que la "decisión" de parar o no en un momento dado debe basarse únicamente en la información presente en el momento , no en ninguna información futura.${\estilo de visualización n}$${\estilo de visualización n}$

Sea una variable aleatoria, que se define en el espacio de probabilidad filtrado con valores en . En la mayoría de los casos, . Entonces se denomina tiempo de detención (con respecto a la filtración ), si se cumple la siguiente condición:${\estilo de visualización \tau}$ ${\displaystyle (\Omega ,{\mathcal {F}},({\mathcal {F}}_{t})_{t\in T},P)}$${\estilo de visualización T}$${\displaystyle T=[0,+\infty )}$${\estilo de visualización \tau}$ ${\displaystyle \mathbb {F} = ({\mathcal {F}}_{t})_{t\in T}}$

${\displaystyle \{\tau \leq t\}\in {\mathcal {F}}_{t}}$a pesar de${\displaystyle t\en T}$

Sea una variable aleatoria, que se define en el espacio de probabilidad filtrado con valores en . Entonces se denomina tiempo de detención si el proceso estocástico , definido por${\estilo de visualización \tau}$ ${\displaystyle (\Omega ,{\mathcal {F}},({\mathcal {F}}_{t})_{t\in T},P)}$${\estilo de visualización T}$${\estilo de visualización \tau}$ ${\displaystyle X=(X_{t})_{t\en T}}$

${\displaystyle X_{t}:={\begin{cases}1&{\text{ si }}t<\tau \\0&{\text{ si }}t\geq \tau \end{cases}}}$

se adapta a la filtración${\displaystyle \mathbb {F} = ({\mathcal {F}}_{t})_{t\in T}}$

Algunos autores excluyen explícitamente los casos en los que puede ser , mientras que otros autores permiten tomar cualquier valor en el cierre de .${\estilo de visualización \tau}$${\estilo de visualización +\infty}$${\estilo de visualización \tau}$${\estilo de visualización T}$

Para ilustrar algunos ejemplos de momentos aleatorios que detienen las reglas y otros que no, considere a un jugador que juega a la ruleta con una ventaja de la casa típica, comenzando con $100 y apostando $1 al rojo en cada juego:

• Jugar exactamente cinco juegos corresponde al tiempo de detención τ  = 5, y es una regla de detención.
• Jugar hasta quedarse sin dinero o hasta haber jugado 500 juegos es una regla de detención.
• Jugar hasta obtener la máxima cantidad de ventaja que jamás podrán tener no es una regla de detención y no proporciona un tiempo de detención, ya que requiere información sobre el futuro, así como sobre el presente y el pasado.
• Jugar hasta duplicar su dinero (tomando prestado si es necesario) no es una regla de detención, ya que existe una probabilidad positiva de que nunca dupliquen su dinero. ^{[ aclaración necesaria (ver discusión ) ]}
• Jugar hasta duplicar su dinero o quedarse sin dinero es una regla de detención, aunque potencialmente no haya límite para la cantidad de juegos que juegan, ya que la probabilidad de que dejen de jugar en un tiempo finito es 1.

Para ilustrar la definición más general del tiempo de parada, considere el movimiento browniano , que es un proceso estocástico , donde cada es una variable aleatoria definida en el espacio de probabilidad . Definimos una filtración en este espacio de probabilidad al dejar que sea el σ -álgebra generado por todos los conjuntos de la forma donde y es un conjunto de Borel . Intuitivamente, un evento E está en si y solo si podemos determinar si E es verdadero o falso simplemente observando el movimiento browniano desde el tiempo 0 hasta el tiempo t . ${\displaystyle (B_{t})_{t\geq 0}}$$Estilo de visualización B_{t}}$${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$${\displaystyle {\mathcal {F}}_{t}}$${\displaystyle (B_{s})^{-1}(A)}$${\displaystyle 0\leq s\leq t}$${\displaystyle A\subseteq \mathbb {R}}$${\displaystyle {\mathcal {F}}_{t}}$

• Toda constante es (trivialmente) un tiempo de detención; corresponde a la regla de detención "detenerse en el tiempo ".${\displaystyle \tau :=t_{0}}$$estilo de visualización t_{0}}$
• Sea entonces un tiempo de detención para el movimiento browniano, correspondiente a la regla de detención: "detenerse tan pronto como el movimiento browniano alcance el valor a ".${\displaystyle a\in \mathbb {R} .}$${\displaystyle \tau :=\inf\{t\geq 0\mid B_{t}=a\}}$
• Otro tiempo de parada viene dado por . Corresponde a la regla de parada "detenerse tan pronto como el movimiento browniano haya sido positivo a lo largo de un tramo contiguo de longitud 1 unidad de tiempo".${\displaystyle \tau :=\inf\{t\geq 1\mid B_{s}>0{\text{ for all }}s\in [t-1,t]\}}$
• En general, si τ ₁ y τ ₂ son tiempos de parada en entonces su mínimo , su máximo y su suma τ ₁  +  τ ₂ también son tiempos de parada. (Esto no es cierto para las diferencias y los productos, porque estos pueden requerir "mirar hacia el futuro" para determinar cuándo detenerse).${\displaystyle \left(\Omega ,{\mathcal {F}},\left\{{\mathcal {F}}_{t}\right\}_{t\geq 0},\mathbb {P} \right)}$${\displaystyle \tau _{1}\wedge \tau _{2}}$${\displaystyle \tau _{1}\vee \tau _{2}}$

Los tiempos de impacto como el segundo ejemplo anterior pueden ser ejemplos importantes de tiempos de detención. Si bien es relativamente sencillo demostrar que, esencialmente, todos los tiempos de detención son tiempos de impacto, ^[2] puede ser mucho más difícil demostrar que un determinado tiempo de impacto es un tiempo de detención. Los últimos tipos de resultados se conocen como el teorema de Début .

Los tiempos de detención se utilizan con frecuencia para generalizar ciertas propiedades de los procesos estocásticos a situaciones en las que la propiedad requerida se satisface solo en un sentido local. En primer lugar, si X es un proceso y τ es un tiempo de detención, entonces X ^τ se utiliza para indicar que el proceso X se detuvo en el tiempo τ .

${\displaystyle X_{t}^{\tau }=X_{\min(t,\tau )}}$

Entonces, se dice que X satisface localmente alguna propiedad P si existe una secuencia de tiempos de detención τ _n , que aumenta hasta el infinito y para la cual los procesos

${\displaystyle \mathbf {1} _{\{\tau _{n}>0\}}X^{\tau _{n}}}$

satisfacen la propiedad P. Algunos ejemplos comunes, con índice de tiempo I = [0, ∞), son los siguientes:

Proceso martingala local . Un proceso X es una martingala local si es càdlàg ^{[ aclaración necesaria ]} y existe una secuencia de tiempos de parada τ _n crecientes hasta el infinito, de modo que

${\displaystyle \mathbf {1} _{\{\tau _{n}>0\}}X^{\tau _{n}}}$

es una martingala para cada n .

Proceso localmente integrable . Un proceso no negativo y creciente X es localmente integrable si existe una secuencia de tiempos de parada τ _n crecientes hasta el infinito, tales que

${\displaystyle \operatorname {E} \left[\mathbf {1} _{\{\tau _{n}>0\}}X^{\tau _{n}}\right]<\infty }$

para cada n .

Los tiempos de parada, con el índice de tiempo establecido I = [0,∞), a menudo se dividen en varios tipos dependiendo de si es posible predecir cuándo están a punto de ocurrir.

Un tiempo de parada τ es predecible si es igual al límite de una secuencia creciente de tiempos de parada τ _n que satisfacen τ _n < τ siempre que τ > 0. Se dice que la secuencia τ _n anuncia τ , y los tiempos de parada predecibles a veces se conocen como anunciables . Ejemplos de tiempos de parada predecibles son los tiempos de impacto de procesos continuos y adaptados . Si τ es el primer momento en el que un proceso continuo y de valor real X es igual a algún valor a , entonces se anuncia mediante la secuencia τ _n , donde τ _n es el primer momento en el que X está dentro de una distancia de 1/ n de a .

Los tiempos de parada accesibles son aquellos que pueden ser cubiertos por una secuencia de tiempos predecibles. Es decir, el tiempo de parada τ es accesible si, P( τ = τ _n para algún n ) = 1, donde τ _n son tiempos predecibles.

Un tiempo de parada τ es totalmente inaccesible si nunca puede ser anunciado por una secuencia creciente de tiempos de parada. Equivalentemente, P( τ = σ < ∞) = 0 para cada tiempo predecible σ . Ejemplos de tiempos de parada totalmente inaccesibles incluyen los tiempos de salto de los procesos de Poisson .

Cada tiempo de parada τ puede descomponerse de forma única en un tiempo accesible y uno totalmente inaccesible. Es decir, existe un único tiempo de parada accesible σ y un tiempo totalmente inaccesible υ tales que τ = σ siempre que σ < ∞, τ = υ siempre que υ < ∞ y τ = ∞ siempre que σ = υ = ∞. Nótese que en el enunciado de este resultado de descomposición, los tiempos de parada no tienen por qué ser casi seguramente finitos, y pueden ser iguales a ∞.

Los ensayos clínicos en medicina suelen realizar análisis intermedios para determinar si el ensayo ya ha cumplido con sus criterios de valoración. Sin embargo, los análisis intermedios generan el riesgo de resultados falsos positivos y, por lo tanto, se utilizan límites de detención para determinar la cantidad y el momento del análisis intermedio (también conocido como gasto alfa, para indicar la tasa de falsos positivos). En cada una de las pruebas intermedias R, el ensayo se detiene si la probabilidad es inferior a un umbral p, que depende del método utilizado. Consulte Análisis secuencial .

• Parada óptima
• Algoritmo de probabilidades
• Problema de secretaria
• Tiempo de golpeo
• Proceso detenido
• Problema de desorden
• Teorema de debut
• Análisis secuencial

• Thomas S. Ferguson , “¿Quién resolvió el problema de la secretaria?”, Stat. Sci. vol. 4, 282–296, (1989).
• Una introducción a los tiempos de parada.
• F. Thomas Bruss , “Suma las probabilidades a uno y deténte”, Anales de probabilidad, vol. 4, 1384-1391, (2000)
• Chung, Kai Lai (1982). Conferencias desde los procesos de Markov hasta el movimiento browniano . Grundlehren der Mathematischen Wissenschaften No. 249. Nueva York, NY: Springer-Verlag. ISBN 978-0-387-90618-8.
• H. Vincent Poor y Olympia Hadjiliadis (2008). Quickest Detection (Primera edición). Cambridge, Inglaterra: Cambridge University Press. ISBN 978-0-521-62104-5.
• Protter, Philip E. (2005). Integración estocástica y ecuaciones diferenciales . Stochastic Modelling and Applied Probability No. 21 (2.ª edición (versión 2.1, 3.ª impresión corregida) ed.). Berlín: Springer-Verlag. ISBN 978-3-540-00313-7.
• Shiryaev, Albert N. (2007). Reglas de detención óptimas . Springer. ISBN 978-3-540-74010-0.