Red reguladora de genes
Colección de reguladores moleculares

Estructura de una red reguladora de genes
Proceso de control de una red reguladora de genes

Una red reguladora de genes (o genética ) ( GRN ) es un conjunto de reguladores moleculares que interactúan entre sí y con otras sustancias en la célula para regular los niveles de expresión génica del ARNm y las proteínas que, a su vez, determinan la función de la célula. La GRN también desempeña un papel central en la morfogénesis , la creación de estructuras corporales, que a su vez es fundamental para la biología del desarrollo evolutivo (evo-devo).

El regulador puede ser ADN , ARN , proteína o cualquier combinación de dos o más de estos tres que formen un complejo, como una secuencia específica de ADN y un factor de transcripción para activar esa secuencia. La interacción puede ser directa o indirecta (a través del ARN transcrito o la proteína traducida). En general, cada molécula de ARNm pasa a formar una proteína específica (o un conjunto de proteínas). En algunos casos, esta proteína será estructural y se acumulará en la membrana celular o dentro de la célula para darle propiedades estructurales particulares. En otros casos, la proteína será una enzima , es decir, una micromáquina que cataliza una determinada reacción, como la descomposición de una fuente de alimento o una toxina. Sin embargo, algunas proteínas solo sirven para activar otros genes, y estos son los factores de transcripción que son los principales actores en las redes o cascadas reguladoras. Al unirse a la región promotora al comienzo de otros genes, los activan, iniciando la producción de otra proteína, y así sucesivamente. Algunos factores de transcripción son inhibidores. [1]

En los organismos unicelulares, las redes reguladoras responden al entorno externo, optimizando la supervivencia de la célula en un momento dado. Así, una célula de levadura, al encontrarse en una solución de azúcar, activará genes para producir enzimas que transformen el azúcar en alcohol. [2] Este proceso, que asociamos con la elaboración del vino, es el modo en que la célula de levadura se gana la vida, obteniendo energía para multiplicarse, lo que en circunstancias normales mejoraría sus perspectivas de supervivencia.

En los animales multicelulares, el mismo principio se ha aplicado a las cascadas de genes que controlan la forma del cuerpo. [3] Cada vez que una célula se divide, se obtienen dos células que, aunque contienen el mismo genoma completo, pueden diferir en qué genes se activan y producen proteínas. A veces, un "bucle de retroalimentación autosostenido" garantiza que una célula mantenga su identidad y la transmita. Menos conocido es el mecanismo de la epigenética por el cual la modificación de la cromatina puede proporcionar memoria celular al bloquear o permitir la transcripción. Una característica importante de los animales multicelulares es el uso de gradientes de morfógenos , que en efecto proporcionan un sistema de posicionamiento que le dice a una célula en qué parte del cuerpo se encuentra y, por lo tanto, en qué tipo de célula convertirse. Un gen que se activa en una célula puede generar un producto que sale de la célula y se difunde a través de las células adyacentes, entrando en ellas y activando genes solo cuando está presente por encima de un cierto nivel umbral. De este modo, estas células son inducidas a un nuevo destino e incluso pueden generar otros morfógenos que envían señales a la célula original. En distancias más largas, los morfógenos pueden utilizar el proceso activo de transducción de señales . Dicha señalización controla la embriogénesis , la construcción de un plan corporal desde cero a través de una serie de pasos secuenciales. También controlan y mantienen los cuerpos adultos a través de procesos de retroalimentación , y la pérdida de dicha retroalimentación debido a una mutación puede ser responsable de la proliferación celular que se observa en el cáncer . En paralelo con este proceso de construcción de la estructura, la cascada genética activa genes que producen proteínas estructurales que le dan a cada célula las propiedades físicas que necesita.

Descripción general

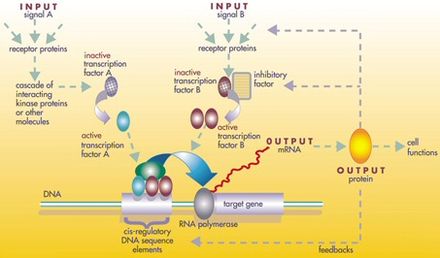
En un nivel, las células biológicas pueden considerarse como "bolsas parcialmente mezcladas" de sustancias químicas biológicas: en el análisis de las redes de regulación genética, estas sustancias químicas son principalmente los ARN mensajeros (ARNm) y las proteínas que surgen de la expresión genética. Estos ARNm y proteínas interactúan entre sí con diversos grados de especificidad. Algunos se difunden por la célula. Otros se unen a las membranas celulares e interactúan con moléculas del entorno. Y otros atraviesan las membranas celulares y median señales de largo alcance a otras células en un organismo multicelular. Estas moléculas y sus interacciones componen una red de regulación genética . Una red de regulación genética típica se parece a esto:

Ejemplo de una red reguladora

Los nodos de esta red pueden representar genes, proteínas, ARNm, complejos proteína/proteína o procesos celulares. Los nodos que se representan a lo largo de líneas verticales están asociados con las interfaces célula/ambiente, mientras que los demás flotan libremente y pueden difundirse . Los bordes entre nodos representan interacciones entre los nodos, que pueden corresponder a reacciones moleculares individuales entre ADN, ARNm, miARN, proteínas o procesos moleculares a través de los cuales los productos de un gen afectan a los de otro, aunque la falta de información obtenida experimentalmente a menudo implica que algunas reacciones no se modelan con un nivel de detalle tan fino. Estas interacciones pueden ser inductivas (generalmente representadas por puntas de flecha o el signo +), con un aumento en la concentración de uno que conduce a un aumento en el otro, inhibidoras (representadas con círculos rellenos, flechas romas o el signo menos), con un aumento en uno que conduce a una disminución en el otro, o duales, cuando dependiendo de las circunstancias el regulador puede activar o inhibir el nodo objetivo. Los nodos pueden regularse a sí mismos directa o indirectamente, creando bucles de retroalimentación, que forman cadenas cíclicas de dependencias en la red topológica. La estructura de la red es una abstracción de la dinámica molecular o química del sistema, que describe las múltiples formas en que una sustancia afecta a todas las demás a las que está conectada. En la práctica, dichas GRN se infieren de la literatura biológica sobre un sistema dado y representan una destilación del conocimiento colectivo sobre un conjunto de reacciones bioquímicas relacionadas. Para acelerar la curación manual de las GRN, algunos esfuerzos recientes intentan utilizar minería de texto , bases de datos curadas, inferencia de redes a partir de datos masivos, verificación de modelos y otras tecnologías de extracción de información para este propósito. [4]

Los genes pueden considerarse como nodos en la red, siendo las entradas proteínas como los factores de transcripción y las salidas el nivel de expresión génica . El valor del nodo depende de una función que depende del valor de sus reguladores en pasos de tiempo anteriores (en la red booleana descrita a continuación, estas son funciones booleanas , típicamente AND, OR y NOT). Estas funciones se han interpretado como la realización de un tipo de procesamiento de información dentro de la célula, que determina el comportamiento celular. Los impulsores básicos dentro de las células son las concentraciones de algunas proteínas, que determinan las coordenadas espaciales (ubicación dentro de la célula o tejido) y temporales (ciclo celular o etapa de desarrollo) de la célula, como una especie de "memoria celular". Las redes génicas recién están comenzando a entenderse, y el siguiente paso para la biología es intentar deducir las funciones de cada "nodo" génico, para ayudar a comprender el comportamiento del sistema en niveles crecientes de complejidad, desde el nivel génico hasta el de la vía de señalización, celular o tisular. [5]

Se han desarrollado modelos matemáticos de GRN para capturar el comportamiento del sistema que se está modelando y, en algunos casos, generar predicciones correspondientes a observaciones experimentales. En otros casos, los modelos han demostrado hacer predicciones novedosas y precisas, que se pueden probar experimentalmente, lo que sugiere nuevos enfoques para explorar en un experimento que a veces no se considerarían en el diseño del protocolo de un laboratorio experimental. Las técnicas de modelado incluyen ecuaciones diferenciales (EDO), redes booleanas, redes de Petri , redes bayesianas , modelos gráficos de redes gaussianas , estocásticos y cálculos de procesos . [6] Por el contrario, se han propuesto técnicas para generar modelos de GRN que expliquen mejor un conjunto de observaciones de series de tiempo . Recientemente, se ha demostrado que la señal ChIP-seq de modificación de histonas está más correlacionada con motivos de factores de transcripción en promotores en comparación con el nivel de ARN. [7] Por lo tanto, se propone que la modificación de histonas de series de tiempo ChIP-seq podría proporcionar una inferencia más confiable de redes reguladoras de genes en comparación con los métodos basados ​​en niveles de expresión.

Estructura y evolución

Característica global

En general, se piensa que las redes reguladoras de genes están formadas por unos pocos nodos altamente conectados ( centros ) y muchos nodos pobremente conectados anidados dentro de un régimen regulador jerárquico. Por lo tanto, las redes reguladoras de genes se aproximan a una topología de red libre de escala jerárquica . [8] Esto es consistente con la visión de que la mayoría de los genes tienen una pleiotropía limitada y operan dentro de módulos reguladores . [9] Se piensa que esta estructura evoluciona debido a la unión preferencial de genes duplicados a genes más altamente conectados. [8] Trabajos recientes también han demostrado que la selección natural tiende a favorecer redes con conectividad dispersa. [10]

Existen principalmente dos formas en las que las redes pueden evolucionar, y ambas pueden ocurrir simultáneamente. La primera es que la topología de la red puede cambiarse mediante la adición o sustracción de nodos (genes) o partes de la red (módulos) pueden expresarse en diferentes contextos. La vía de señalización Hippo de Drosophila proporciona un buen ejemplo. La vía de señalización Hippo controla tanto el crecimiento mitótico como la diferenciación celular postmitótica. [11] Recientemente se descubrió que la red en la que opera la vía de señalización Hippo difiere entre estas dos funciones, lo que a su vez cambia el comportamiento de la vía de señalización Hippo. Esto sugiere que la vía de señalización Hippo opera como un módulo regulador conservado que puede usarse para múltiples funciones según el contexto. [11] Por lo tanto, cambiar la topología de la red puede permitir que un módulo conservado cumpla múltiples funciones y altere el resultado final de la red. La segunda forma en que las redes pueden evolucionar es cambiando la fuerza de las interacciones entre nodos, como la fuerza con la que un factor de transcripción puede unirse a un elemento regulador cis . Se ha demostrado que dicha variación en la fuerza de los bordes de la red subyace a la variación entre especies en el patrón de destino de las células de la vulva de los gusanos Caenorhabditis . [12]

Característica local

Bucle de retroalimentación

Otra característica ampliamente citada de la red reguladora de genes es su abundancia de ciertas subredes repetitivas conocidas como motivos de red . Los motivos de red pueden considerarse como patrones topológicos repetitivos al dividir una red grande en bloques pequeños. Análisis previos encontraron varios tipos de motivos que aparecieron con mayor frecuencia en redes reguladoras de genes que en redes generadas aleatoriamente. [13] [14] [15] Como ejemplo, uno de estos motivos se llama bucles de avance, que constan de tres nodos. Este motivo es el más abundante entre todos los motivos posibles compuestos de tres nodos, como se muestra en las redes reguladoras de genes de la mosca, el nematodo y el ser humano. [15]

Se ha propuesto que los motivos enriquecidos sigan una evolución convergente , lo que sugiere que son "diseños óptimos" para ciertos fines regulatorios. [16] Por ejemplo, el modelado muestra que los bucles de avance pueden coordinar el cambio en el nodo A (en términos de concentración y actividad) y la dinámica de expresión del nodo C, creando diferentes comportamientos de entrada-salida. [17] [18] El sistema de utilización de galactosa de E. coli contiene un bucle de avance que acelera la activación del operón de utilización de galactosa galETK , lo que facilita potencialmente la transición metabólica a galactosa cuando se agota la glucosa. [19] El bucle de avance en los sistemas de utilización de arabinosa de E. coli retrasa la activación del operón del catabolismo de la arabinosa y los transportadores, evitando potencialmente la transición metabólica innecesaria debido a fluctuaciones temporales en las vías de señalización ascendentes. [20] De manera similar, en la vía de señalización Wnt de Xenopus , el bucle de avance actúa como un detector de cambio de pliegue que responde al cambio de pliegue, en lugar del cambio absoluto, en el nivel de β-catenina, lo que aumenta potencialmente la resistencia a las fluctuaciones en los niveles de β-catenina. [21] Siguiendo la hipótesis de la evolución convergente, el enriquecimiento de los bucles de avance sería una adaptación para una respuesta rápida y resistencia al ruido. Una investigación reciente encontró que la levadura cultivada en un entorno de glucosa constante desarrolló mutaciones en las vías de señalización de la glucosa y la vía de regulación del crecimiento, lo que sugiere que los componentes reguladores que responden a los cambios ambientales son prescindibles en un entorno constante. [22]

Por otra parte, algunos investigadores plantean la hipótesis de que el enriquecimiento de los motivos de la red no es adaptativo. [23] En otras palabras, las redes reguladoras de genes pueden evolucionar hacia una estructura similar sin la selección específica en el comportamiento de entrada-salida propuesto. El apoyo a esta hipótesis a menudo proviene de simulaciones computacionales. Por ejemplo, las fluctuaciones en la abundancia de bucles de retroalimentación en un modelo que simula la evolución de las redes reguladoras de genes mediante el reconectado aleatorio de nodos pueden sugerir que el enriquecimiento de los bucles de retroalimentación es un efecto secundario de la evolución. [24] En otro modelo de evolución de las redes reguladoras de genes, la relación de las frecuencias de duplicación y eliminación de genes muestra una gran influencia en la topología de la red: ciertas relaciones conducen al enriquecimiento de los bucles de retroalimentación y crean redes que muestran características de redes libres de escala jerárquica. Se ha demostrado computacionalmente la evolución de novo de bucles de propagación hacia adelante coherentes de tipo 1 en respuesta a la selección por su función hipotética de filtrar una señal espuria corta, lo que respalda la evolución adaptativa, pero para el ruido no idealizado, se favoreció en cambio un sistema basado en dinámica de regulación hacia adelante con una topología diferente. [25]

Redes reguladoras bacterianas

Las redes reguladoras permiten a las bacterias adaptarse a casi todos los nichos ambientales de la Tierra. [26] [27] Las bacterias utilizan una red de interacciones entre diversos tipos de moléculas, como ADN, ARN, proteínas y metabolitos, para lograr la regulación de la expresión génica. En las bacterias, la función principal de las redes reguladoras es controlar la respuesta a los cambios ambientales, por ejemplo, el estado nutricional y el estrés ambiental. [28] Una organización compleja de redes permite al microorganismo coordinar e integrar múltiples señales ambientales. [26]

Un ejemplo de estrés es cuando el entorno se vuelve repentinamente pobre en nutrientes. Esto desencadena un proceso complejo de adaptación en bacterias , como E. coli . Después de este cambio ambiental, miles de genes cambian el nivel de expresión. Sin embargo, estos cambios son predecibles a partir de la topología y la lógica de la red genética [29] que se informa en RegulonDB . Específicamente, en promedio, la fuerza de respuesta de un gen era predecible a partir de la diferencia entre los números de factores de transcripción de entrada activadores y represores de ese gen. [29]

Modelado

Ecuaciones diferenciales ordinarias acopladas

Es común modelar una red de este tipo con un conjunto de ecuaciones diferenciales ordinarias (EDO) acopladas o EDS , que describen la cinética de reacción de las partes constituyentes. Supongamos que nuestra red reguladora tiene nodos y que represente las concentraciones de las sustancias correspondientes en el tiempo . Entonces la evolución temporal del sistema se puede describir aproximadamente mediante norte {\estilo de visualización N} S 1 ( a ) , S 2 ( a ) , … , S norte ( a ) {\displaystyle S_{1}(t),S_{2}(t),\ldots ,S_{N}(t)} norte {\estilo de visualización N} a {\estilo de visualización t}

d S yo d a = F yo ( S 1 , S 2 , … , S norte ) {\displaystyle {\frac {dS_{j}}{dt}}=f_{j}\left(S_{1},S_{2},\ldots ,S_{N}\right)}

donde las funciones expresan la dependencia de las concentraciones de otras sustancias presentes en la célula. Las funciones se derivan en última instancia de los principios básicos de la cinética química o expresiones simples derivadas de estos, por ejemplo , la cinética enzimática de Michaelis-Menten . Por lo tanto, las formas funcionales de los se eligen generalmente como polinomios de orden bajo o funciones de Hill que sirven como ansatz para la dinámica molecular real. Dichos modelos se estudian luego utilizando las matemáticas de la dinámica no lineal . La información específica del sistema, como las constantes de velocidad de reacción y las sensibilidades, se codifican como parámetros constantes. [30] F yo estilo de visualización f_ {j}} S yo Estilo de visualización S_ {j}} F yo estilo de visualización f_ {j}} F yo estilo de visualización f_ {j}}

Resolviendo el punto fijo del sistema:

d S yo d a = 0 {\displaystyle {\frac {dS_{j}}{dt}}=0}

para todos , se obtienen (posiblemente varios) perfiles de concentración de proteínas y ARNm que son teóricamente sostenibles (aunque no necesariamente estables ). Los estados estacionarios de las ecuaciones cinéticas corresponden así a tipos celulares potenciales, y las soluciones oscilatorias de la ecuación anterior a tipos celulares naturalmente cíclicos. La estabilidad matemática de estos atractores puede caracterizarse habitualmente por el signo de derivadas superiores en puntos críticos, y luego corresponder a la estabilidad bioquímica del perfil de concentración. Los puntos críticos y las bifurcaciones en las ecuaciones corresponden a estados celulares críticos en los que pequeñas perturbaciones de estado o parámetro podrían cambiar el sistema entre uno de varios destinos de diferenciación estables. Las trayectorias corresponden al desarrollo de vías biológicas y los transitorios de las ecuaciones a eventos biológicos de corto plazo. Para una discusión más matemática, véanse los artículos sobre no linealidad , sistemas dinámicos , teoría de la bifurcación y teoría del caos . yo {\estilo de visualización j}

Red booleana

El siguiente ejemplo ilustra cómo una red booleana puede modelar una red reguladora genética junto con sus productos genéticos (las salidas) y las sustancias del entorno que la afectan (las entradas). Stuart Kauffman fue uno de los primeros biólogos en utilizar la metáfora de las redes booleanas para modelar redes reguladoras genéticas. [31] [32]

  1. Cada gen, cada entrada y cada salida está representado por un nodo en un gráfico dirigido en el que hay una flecha de un nodo a otro si y sólo si existe un vínculo causal entre los dos nodos.
  2. Cada nodo del gráfico puede estar en uno de dos estados: encendido o apagado.
  3. Para un gen, "on" corresponde al gen que se expresa; para entradas y salidas, "on" corresponde a la sustancia que está presente.
  4. Se considera que el tiempo transcurre en pasos discretos. En cada paso, el nuevo estado de un nodo es una función booleana de los estados anteriores de los nodos con flechas que apuntan hacia él.

La validez del modelo se puede comprobar comparando los resultados de la simulación con las observaciones de series temporales. Una validación parcial de un modelo de red booleana también puede provenir de la comprobación de la existencia prevista de una conexión reguladora aún desconocida entre dos factores de transcripción particulares que son cada uno nodos del modelo. [33]

Redes continuas

Los modelos de red continua de GRN son una extensión de las redes booleanas descritas anteriormente. Los nodos aún representan genes y conexiones entre ellos, influencias reguladoras en la expresión génica. Los genes en sistemas biológicos muestran un rango continuo de niveles de actividad y se ha argumentado que el uso de una representación continua captura varias propiedades de las redes reguladoras génicas que no están presentes en el modelo booleano. [34] Formalmente, la mayoría de estos enfoques son similares a una red neuronal artificial , ya que las entradas a un nodo se suman y el resultado sirve como entrada a una función sigmoidea , por ejemplo, [35] pero las proteínas a menudo controlan la expresión génica de una manera sinérgica, es decir, no lineal. [36] Sin embargo, ahora existe un modelo de red continua [37] que permite agrupar las entradas a un nodo, logrando así otro nivel de regulación. Este modelo está formalmente más cerca de una red neuronal recurrente de orden superior . El mismo modelo también se ha utilizado para imitar la evolución de la diferenciación celular [38] e incluso la morfogénesis multicelular . [39]

Redes genéticas estocásticas

Los resultados experimentales [40] [41] han demostrado que la expresión génica es un proceso estocástico. Por ello, muchos autores están utilizando ahora el formalismo estocástico, tras el trabajo de Arkin et al. [42] Los trabajos sobre la expresión génica individual [43] y sobre pequeñas redes genéticas sintéticas [44] [45], como el interruptor genético de Tim Gardner y Jim Collins , proporcionaron datos experimentales adicionales sobre la variabilidad fenotípica y la naturaleza estocástica de la expresión génica. Las primeras versiones de los modelos estocásticos de expresión génica implicaban únicamente reacciones instantáneas y estaban impulsadas por el algoritmo de Gillespie . [46]

Dado que algunos procesos, como la transcripción genética, implican muchas reacciones y no se pueden modelar correctamente como una reacción instantánea en un solo paso, se propuso modelar estas reacciones como reacciones múltiples retardadas de un solo paso para tener en cuenta el tiempo que lleva completar todo el proceso. [47]

A partir de aquí, se propuso un conjunto de reacciones [48] que permiten generar GRN, las cuales luego se simulan utilizando una versión modificada del algoritmo de Gillespie, que puede simular múltiples reacciones retardadas en el tiempo (reacciones químicas donde a cada uno de los productos se le proporciona un retardo temporal que determina cuándo será liberado en el sistema como un "producto terminado").

Por ejemplo, la transcripción básica de un gen se puede representar mediante la siguiente reacción de un solo paso (RNAP es la ARN polimerasa, RBS es el sitio de unión del ribosoma del ARN y Pro i es la región promotora del gen i ): 

ARN polimerasa + Pro i ⟶ a i , b a s Pro i ( τ i 1 ) + Banco Central de Rusia i ( τ i 1 ) + ARN polimerasa ( τ i 2 ) {\displaystyle {\text{RNAP}}+{\text{Pro}}_{i}{\overset {k_{i,bas}}{\longrightarrow }}{\text{Pro}}_{i}(\tau _{i}^{1})+{\text{RBS}}_{i}(\tau _{i}^{1})+{\text{RNAP}}(\tau _{i}^{2})}

Además, parece haber una compensación entre el ruido en la expresión genética, la velocidad con la que los genes pueden cambiar y el costo metabólico asociado a su funcionamiento. Más específicamente, para cualquier nivel dado de costo metabólico, existe una compensación óptima entre el ruido y la velocidad de procesamiento y el aumento del costo metabólico conduce a mejores compensaciones entre velocidad y ruido. [49] [50] [51]

Un trabajo reciente propuso un simulador (SGNSim, Stochastic Gene Networks Simulator ), [52] que puede modelar GRN donde la transcripción y la traducción se modelan como múltiples eventos con retraso en el tiempo y su dinámica es impulsada por un algoritmo de simulación estocástica (SSA) capaz de lidiar con múltiples eventos con retraso en el tiempo. Los retrasos en el tiempo se pueden extraer de varias distribuciones y las velocidades de reacción de funciones complejas o de parámetros físicos. SGNSim puede generar conjuntos de GRN dentro de un conjunto de parámetros definidos por el usuario, como la topología. También se puede utilizar para modelar GRN específicos y sistemas de reacciones químicas. También se pueden modelar perturbaciones genéticas como deleciones de genes, sobreexpresión de genes, inserciones y mutaciones por cambio de marco.

El GRN se crea a partir de un grafo con la topología deseada, imponiendo distribuciones de grado de entrada y grado de salida. Las actividades del promotor de genes se ven afectadas por los productos de expresión de otros genes que actúan como entradas, en forma de monómeros o combinados en multímeros y establecidos como directos o indirectos. A continuación, cada entrada directa se asigna a un sitio operador y se puede permitir, o no, que diferentes factores de transcripción compitan por el mismo sitio operador, mientras que a las entradas indirectas se les asigna un objetivo. Finalmente, se asigna una función a cada gen, definiendo la respuesta del gen a una combinación de factores de transcripción (estado del promotor). Las funciones de transferencia (es decir, cómo responden los genes a una combinación de entradas) se pueden asignar a cada combinación de estados del promotor según se desee.

En otros trabajos recientes, se han desarrollado modelos multiescala de redes reguladoras de genes que se centran en aplicaciones de biología sintética. Se han utilizado simulaciones que modelan todas las interacciones biomoleculares en la transcripción, traducción, regulación e inducción de redes reguladoras de genes, guiando el diseño de sistemas sintéticos. [53]

Predicción

Otros trabajos se han centrado en predecir los niveles de expresión génica en una red reguladora de genes. Los enfoques utilizados para modelar redes reguladoras de genes se han visto limitados a ser interpretables y, como resultado, son generalmente versiones simplificadas de la red. Por ejemplo, se han utilizado redes booleanas debido a su simplicidad y capacidad para manejar datos ruidosos, pero pierden información de los datos al tener una representación binaria de los genes. Además, las redes neuronales artificiales omiten el uso de una capa oculta para que puedan interpretarse, perdiendo la capacidad de modelar correlaciones de orden superior en los datos. Utilizando un modelo que no esté limitado a ser interpretable, se puede producir un modelo más preciso. Ser capaz de predecir las expresiones genéticas con mayor precisión proporciona una forma de explorar cómo los fármacos afectan a un sistema de genes, así como de encontrar qué genes están interrelacionados en un proceso. Esto ha sido alentado por la competencia DREAM [54] que promueve una competencia para los mejores algoritmos de predicción. [55] Algunos otros trabajos recientes han utilizado redes neuronales artificiales con una capa oculta. [56]

Aplicaciones

Esclerosis múltiple

Existen tres clases de esclerosis múltiple: recurrente-remitente (EMRR), progresiva primaria (EMPP) y progresiva secundaria (EMSP). La red reguladora de genes (RGG) desempeña un papel fundamental para comprender el mecanismo de la enfermedad en estas tres clases diferentes de esclerosis múltiple. [57]

Véase también

Referencias

  1. ^ Latchman DS (septiembre de 1996). "Factores de transcripción inhibidores". Revista internacional de bioquímica y biología celular . 28 (9): 965–974. doi :10.1016/1357-2725(96)00039-8. PMID  8930119.
  2. ^ Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, et al. (octubre de 2002). "Redes reguladoras de la transcripción en Saccharomyces cerevisiae". Science . 298 (5594). Young Lab: 799–804. Bibcode :2002Sci...298..799L. doi :10.1126/science.1075090. PMID  12399584. S2CID  4841222.
  3. ^ Davidson E, Levin M (abril de 2005). "Redes reguladoras de genes". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 102 (14): 4935. Bibcode :2005PNAS..102.4935D. doi : 10.1073/pnas.0502024102 . PMC 556010 . PMID  15809445. 
  4. ^ Leitner F, Krallinger M, Tripathi S, Kuiper M, Lægreid A, Valencia A (julio de 2013). "Explotación de redes de transcripción cis-regulatorias a partir de la literatura". Actas de BioLINK SIG 2013 : 5–12.
  5. ^ Azpeitia E, Muñoz S, González-Tokman D, Martínez-Sánchez ME, Weinstein N, Naldi A, et al. (febrero de 2017). "La combinación de las funcionalidades de los circuitos de retroalimentación es determinante para el número y tamaño de los atractores en redes booleanas tipo vías". Scientific Reports . 7 : 42023. Bibcode :2017NatSR...742023A. doi :10.1038/srep42023. PMC 5301197 . PMID  28186191. 
  6. ^ Banf M, Rhee SY (enero de 2017). "Inferencia computacional de redes reguladoras de genes: enfoques, limitaciones y oportunidades". Biochimica et Biophysica Acta (BBA) - Mecanismos reguladores de genes . 1860 (1): 41–52. doi : 10.1016/j.bbagrm.2016.09.003 . PMID  27641093.
  7. ^ Kumar V, Muratani M, Rayan NA, Kraus P, Lufkin T, Ng HH, Prabhakar S (julio de 2013). "Procesamiento uniforme y óptimo de señales de datos mapeados de secuenciación profunda". Nature Biotechnology . 31 (7): 615–622. doi : 10.1038/nbt.2596 . PMID  23770639.
  8. ^ ab Barabási AL, Oltvai ZN (febrero de 2004). "Biología de redes: comprensión de la organización funcional de la célula". Nature Reviews. Genética . 5 (2): 101–113. doi :10.1038/nrg1272. PMID  14735121. S2CID  10950726.
  9. ^ Wagner GP, Zhang J (marzo de 2011). "La estructura pleiotrópica del mapa genotipo-fenotipo: la capacidad de evolución de organismos complejos". Nature Reviews. Genetics . 12 (3): 204–213. doi :10.1038/nrg2949. PMID  21331091. S2CID  8612268.
  10. ^ Leclerc RD (agosto de 2008). "Supervivencia de los más dispersos: las redes genéticas robustas son parsimoniosas". Biología de sistemas moleculares . 4 (1): 213. doi :10.1038/msb.2008.52. PMC 2538912 . PMID  18682703. 
  11. ^ ab Jukam D, Xie B, Rister J, Terrell D, Charlton-Perkins M, Pistillo D, et al. (octubre de 2013). "Retroalimentaciones opuestas en la vía Hippo para el control del crecimiento y el destino neuronal". Science . 342 (6155): 1238016. doi :10.1126/science.1238016. PMC 3796000 . PMID  23989952. 
  12. ^ Hoyos E, Kim K, Milloz J, Barkoulas M, Pénigault JB, Munro E, Félix MA (abril de 2011). "Variación cuantitativa en la señalización autocrina y la comunicación entre vías en la red vulvar de Caenorhabditis". Current Biology . 21 (7): 527–538. doi :10.1016/j.cub.2011.02.040. PMC 3084603 . PMID  21458263. 
  13. ^ Shen-Orr SS, Milo R, Mangan S, Alon U (mayo de 2002). "Motivos de red en la red de regulación transcripcional de Escherichia coli". Nature Genetics . 31 (1): 64–68. doi : 10.1038/ng881 . PMID  11967538. S2CID  2180121.
  14. ^ Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, et al. (octubre de 2002). "Redes reguladoras de la transcripción en Saccharomyces cerevisiae". Science . 298 (5594): 799–804. Bibcode :2002Sci...298..799L. doi :10.1126/science.1075090. PMID  12399584. S2CID  4841222.
  15. ^ ab Boyle AP, Araya CL, Brdlik C, Cayting P, Cheng C, Cheng Y, et al. (agosto de 2014). "Análisis comparativo de la información regulatoria y los circuitos entre especies distantes". Nature . 512 (7515): 453–456. Bibcode :2014Natur.512..453B. doi :10.1038/nature13668. PMC 4336544 . PMID  25164757. 
  16. ^ Conant GC, Wagner A (julio de 2003). "Evolución convergente de circuitos genéticos". Nature Genetics . 34 (3): 264–266. doi :10.1038/ng1181. PMID  12819781. S2CID  959172.
  17. ^ Mangan S, Alon U (octubre de 2003). "Estructura y función del motivo de red de bucle de alimentación hacia adelante". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 100 (21): 11980–11985. Bibcode :2003PNAS..10011980M. doi : 10.1073/pnas.2133841100 . PMC 218699 . PMID  14530388. 
  18. ^ Goentoro L, Shoval O, Kirschner MW, Alon U (diciembre de 2009). "El bucle de retroalimentación incoherente puede proporcionar detección de cambios en la regulación génica". Molecular Cell . 36 (5): 894–899. doi :10.1016/j.molcel.2009.11.018. PMC 2896310 . PMID  20005851. 
  19. ^ Mangan S, Itzkovitz S, Zaslaver A, Alon U (marzo de 2006). "El bucle de retroalimentación incoherente acelera el tiempo de respuesta del sistema gal de Escherichia coli". Journal of Molecular Biology . 356 (5): 1073–1081. CiteSeerX 10.1.1.184.8360 . doi :10.1016/j.jmb.2005.12.003. PMID  16406067. 
  20. ^ Mangan S, Zaslaver A, Alon U (noviembre de 2003). "El bucle de retroalimentación coherente sirve como un elemento de retardo sensible a la señal en las redes de transcripción". Journal of Molecular Biology . 334 (2): 197–204. CiteSeerX 10.1.1.110.4629 . doi :10.1016/j.jmb.2003.09.049. PMID  14607112. 
  21. ^ Goentoro L, Kirschner MW (diciembre de 2009). "Evidencia de que el cambio de plegamiento, y no el nivel absoluto, de beta-catenina determina la señalización de Wnt". Molecular Cell . 36 (5): 872–884. doi :10.1016/j.molcel.2009.11.017. PMC 2921914 . PMID  20005849. 
  22. ^ Kvitek DJ, Sherlock G (noviembre de 2013). "La secuenciación de todo el genoma y de toda la población revela que la pérdida de redes de señalización es la principal estrategia adaptativa en un entorno constante". PLOS Genetics . 9 (11): e1003972. doi : 10.1371/journal.pgen.1003972 . PMC 3836717 . PMID  24278038. 
  23. ^ Lynch M (octubre de 2007). "La evolución de las redes genéticas mediante procesos no adaptativos". Nature Reviews. Genética . 8 (10): 803–813. doi :10.1038/nrg2192. PMID  17878896. S2CID  11839414.
  24. ^ Cordero OX, Hogeweg P (octubre de 2006). "Circuitos de bucle de retroalimentación como efecto secundario de la evolución del genoma". Biología molecular y evolución . 23 (10): 1931–1936. doi :10.1093/molbev/msl060. PMID  16840361.
  25. ^ Xiong K, Lancaster AK, Siegal ML, Masel J (junio de 2019). "La regulación de avance evoluciona de forma adaptativa a través de la dinámica en lugar de la topología cuando hay ruido intrínseco". Nature Communications . 10 (1): 2418. Bibcode :2019NatCo..10.2418X. doi :10.1038/s41467-019-10388-6. PMC 6546794 . PMID  31160574. 
  26. ^ ab Filloux AA , ed. (2012). Redes reguladoras bacterianas . Caister Academic Press . ISBN 978-1-908230-03-4.
  27. ^ Gross R, Beier D, eds. (2012). Sistemas de dos componentes en bacterias . Caister Academic Press . ISBN 978-1-908230-08-9.
  28. ^ Requena JM, ed. (2012). Respuesta al estrés en microbiología . Caister Academic Press . ISBN 978-1-908230-04-1.
  29. ^ ab Almeida BL, Bahrudeen MN, Chauhan V, Dash S, Kandavalli V, Häkkinen A, et al. (junio de 2022). "La red de factores de transcripción de E. coli dirige las respuestas globales a los cambios en la concentración de ARN polimerasa". Investigación de ácidos nucleicos . 50 (12): 6801–6819. doi :10.1093/nar/gkac540. PMC 9262627 . PMID  35748858. 
  30. ^ Chu D, Zabet NR, Mitavskiy B (abril de 2009). "Modelos de unión de factores de transcripción: sensibilidad de las funciones de activación a las suposiciones del modelo" (PDF) . Journal of Theoretical Biology . 257 (3): 419–429. Bibcode :2009JThBi.257..419C. doi :10.1016/j.jtbi.2008.11.026. PMID  19121637. S2CID  12809260.
  31. ^ Kauffman SA (1993). Los orígenes del orden . Prensa de la Universidad de Oxford. ISBN 978-0-19-505811-6.
  32. ^ Kauffman SA (marzo de 1969). "Estabilidad metabólica y epigénesis en redes genéticas construidas aleatoriamente". Journal of Theoretical Biology . 22 (3): 437–467. Bibcode :1969JThBi..22..437K. doi :10.1016/0022-5193(69)90015-0. PMID  5803332.
  33. ^ Lovrics A, Gao Y, Juhász B, Bock I, Byrne HM, Dinnyés A, Kovács KA (noviembre de 2014). "El modelado booleano revela nuevas conexiones reguladoras entre los factores de transcripción que orquestan el desarrollo de la médula espinal ventral". PLOS ONE . ​​9 (11): e111430. Bibcode :2014PLoSO...9k1430L. doi : 10.1371/journal.pone.0111430 . PMC 4232242 . PMID  25398016. 
  34. ^ Vohradsky J (septiembre de 2001). "Modelo neuronal de la red genética". The Journal of Biological Chemistry . 276 (39): 36168–36173. doi : 10.1074/jbc.M104391200 . PMID  11395518.
  35. ^ Geard N, Wiles J (2005). "Un modelo de red genética para el desarrollo de linajes celulares". Vida artificial . 11 (3): 249–267. CiteSeerX 10.1.1.1.4742 . doi :10.1162/1064546054407202. PMID  16053570. S2CID  8664677. 
  36. ^ Schilstra MJ, Bolouri H (2 de enero de 2002). "Modelado de la regulación de la expresión génica en redes reguladoras genéticas". Grupo de biocomputación, Universidad de Hertfordshire. Archivado desde el original el 13 de octubre de 2007.
  37. ^ Knabe JF, Nehaniv CL, Schilstra MJ, Quick T (2006). "Evolución de relojes biológicos mediante redes reguladoras genéticas". Actas de la conferencia Artificial Life X (Alife 10) . MIT Press. págs. 15–21. CiteSeerX 10.1.1.72.5016 . 
  38. ^ Knabe JF, Nehaniv CL, Schilstra MJ (2006). "Robustez evolutiva de la diferenciación en redes reguladoras genéticas". Actas del séptimo taller alemán sobre vida artificial 2006 (GWAL-7) . Berlín: Akademische Verlagsgesellschaft AKA . págs. 75–84. CiteSeerX 10.1.1.71.8768 . 
  39. ^ Knabe JF, Schilstra MJ, Nehaniv CL (2008). "Evolución y morfogénesis de organismos multicelulares diferenciados: gradientes de difusión generados de forma autónoma para información posicional" (PDF) . Vida artificial XI: Actas de la undécima conferencia internacional sobre simulación y síntesis de sistemas vivos . MIT Press.
  40. ^ Elowitz MB, Levine AJ, Siggia ED, Swain PS (agosto de 2002). "Expresión génica estocástica en una sola célula". Science . 297 (5584): 1183–1186. Bibcode :2002Sci...297.1183E. doi :10.1126/science.1070919. PMID  12183631. S2CID  10845628.
  41. ^ Blake WJ, KAErn M, Cantor CR, Collins JJ (abril de 2003). "Ruido en la expresión génica eucariota". Nature . 422 (6932): 633–637. Bibcode :2003Natur.422..633B. doi :10.1038/nature01546. PMID  12687005. S2CID  4347106.
  42. ^ Arkin A, Ross J, McAdams HH (agosto de 1998). "Análisis cinético estocástico de la bifurcación de la vía de desarrollo en células de Escherichia coli infectadas con el fago lambda". Genética . 149 (4): 1633–1648. doi :10.1093/genetics/149.4.1633. PMC 1460268 . PMID  9691025. 
  43. ^ Raser JM, O'Shea EK (septiembre de 2005). "El ruido en la expresión génica: orígenes, consecuencias y control". Science . 309 (5743): 2010–2013. Bibcode :2005Sci...309.2010R. doi :10.1126/science.1105891. PMC 1360161 . PMID  16179466. 
  44. ^ Elowitz MB, Leibler S (enero de 2000). "Una red oscilatoria sintética de reguladores transcripcionales". Nature . 403 (6767): 335–338. Bibcode :2000Natur.403..335E. doi :10.1038/35002125. PMID  10659856. S2CID  41632754.
  45. ^ Gardner TS, Cantor CR, Collins JJ (enero de 2000). "Construcción de un interruptor genético en Escherichia coli". Nature . 403 (6767): 339–342. Bibcode :2000Natur.403..339G. doi :10.1038/35002131. PMID  10659857. S2CID  345059.
  46. ^ Gillespie DT (1976). "Un método general para simular numéricamente la evolución temporal estocástica de reacciones químicas acopladas". J. Comput. Phys . 22 (4): 403–34. Bibcode :1976JCoPh..22..403G. doi :10.1016/0021-9991(76)90041-3.
  47. ^ Roussel MR, Zhu R (diciembre de 2006). "Validación de un algoritmo para la simulación estocástica de retardo de la transcripción y la traducción en la expresión génica procariota". Biología física . 3 (4): 274–284. Bibcode :2006PhBio...3..274R. doi :10.1088/1478-3975/3/4/005. PMID  17200603. S2CID  21456299.
  48. ^ Ribeiro A, Zhu R, Kauffman SA (noviembre de 2006). "Una estrategia general de modelado para redes reguladoras de genes con dinámica estocástica". Journal of Computational Biology . 13 (9): 1630–1639. doi :10.1089/cmb.2006.13.1630. PMID  17147485. S2CID  6629364.
  49. ^ Zabet NR, Chu DF (junio de 2010). "Límites computacionales para genes binarios". Journal of the Royal Society, Interface . 7 (47): 945–954. doi :10.1098/rsif.2009.0474. PMC 2871807 . PMID  20007173. 
  50. ^ Chu DF, Zabet NR, Hone AN (mayo-junio de 2011). "Configuración óptima de parámetros para el procesamiento de información en redes reguladoras de genes" (PDF) . Bio Systems . 104 (2–3): 99–108. Bibcode :2011BiSys.104...99C. doi :10.1016/j.biosystems.2011.01.006. PMID  21256918.
  51. ^ Zabet NR (septiembre de 2011). "Retroalimentación negativa y límites físicos de los genes". Journal of Theoretical Biology . 284 (1): 82–91. arXiv : 1408.1869 . Bibcode :2011JThBi.284...82Z. doi :10.1016/j.jtbi.2011.06.021. PMID  21723295. S2CID  14274912.
  52. ^ Ribeiro AS, Lloyd-Price J (marzo de 2007). "SGN Sim, un simulador de redes genéticas estocásticas". Bioinformática . 23 (6): 777–779. doi : 10.1093/bioinformatics/btm004 . PMID  17267430.
  53. ^ Kaznessis YN (noviembre de 2007). "Modelos para biología sintética". BMC Systems Biology . 1 : 47. doi : 10.1186/1752-0509-1-47 . PMC 2194732 . PMID  17986347. 
  54. ^ "El proyecto DREAM". Centro de análisis multiescala de redes genómicas y celulares (MAGNet) de la Universidad de Columbia.
  55. ^ Gustafsson M, Hörnquist M (febrero de 2010). "Predicción de la expresión génica mediante integración suave y el mejor rendimiento neto elástico del desafío de expresión génica DREAM3". PLOS ONE . ​​5 (2): e9134. Bibcode :2010PLoSO...5.9134G. doi : 10.1371/journal.pone.0009134 . PMC 2821917 . PMID  20169069. 
  56. ^ Smith MR, Clement M, Martinez T, Snell Q (2010). "Predicción de la expresión génica en series temporales utilizando redes neuronales con capas ocultas" (PDF) . Actas del 7.º Simposio de Biotecnología y Bioinformática (BIOT 2010) . pp. 67–69.
  57. ^ Gnanakkumaar P, Murugesan R, Ahmed SS (septiembre de 2019). "Las redes reguladoras de genes en células mononucleares periféricas revelan módulos reguladores críticos y reguladores de la esclerosis múltiple". Scientific Reports . 9 (1): 12732. Bibcode :2019NatSR...912732G. doi :10.1038/s41598-019-49124-x. PMC 6726613 . PMID  31484947. 

Lectura adicional

  • Bolouri H, Bower JM (2001). Modelado computacional de redes genéticas y bioquímicas . Cambridge, Mass.: MIT Press. ISBN 978-0-262-02481-5.
  • Kauffman SA (marzo de 1969). "Estabilidad metabólica y epigénesis en redes genéticas construidas aleatoriamente". Journal of Theoretical Biology . 22 (3): 437–467. Bibcode :1969JThBi..22..437K. doi :10.1016/0022-5193(69)90015-0. PMID  5803332.
  • Base de datos de factores de transcripción de plantas y plataforma de análisis y datos de regulación transcripcional de plantas
  • Servicio web de código abierto para análisis de GRN
  • BIB: Navegador de interacción biológica de levaduras
  • Modelos gaussianos gráficos para datos genómicos: inferencia de redes de asociación de genes con GGM
  • Una bibliografía sobre el aprendizaje de redes causales de interacciones genéticas: se actualiza periódicamente y contiene cientos de enlaces a artículos de bioinformática, estadística y aprendizaje automático.
  • BIOREL es un recurso basado en la web para la estimación cuantitativa del sesgo de la red genética en relación con la información de bases de datos disponible sobre actividad/función/propiedades/asociaciones/interacción de los genes.
  • Relojes biológicos en evolución mediante redes reguladoras genéticas: página de información con código fuente del modelo y subprograma Java.
  • Redes de genes diseñados
  • Tutorial: Algoritmos genéticos y su aplicación a la evolución artificial de redes reguladoras genéticas
  • BEN: un recurso basado en la web para explorar las conexiones entre genes, enfermedades y otras entidades biomédicas
  • Red global de interacción proteína-proteína y regulación genética de Arabidopsis thaliana Archivado el 16 de marzo de 2016 en Wayback Machine
Obtenido de "https://es.wikipedia.org/w/index.php?title=Red_reguladora_genética&oldid=1227557493"