Ciclo de eclipses

Los eclipses pueden ocurrir repetidamente, separados por ciertos intervalos de tiempo: estos intervalos se denominan ciclos de eclipses . [1] La serie de eclipses separados por una repetición de uno de estos intervalos se denomina serie de eclipses .
Condiciones de eclipse

Los eclipses pueden ocurrir cuando la Tierra y la Luna están alineadas con el Sol , y la sombra de un cuerpo proyectada por el Sol cae sobre el otro. Así, en la luna nueva , cuando la Luna está en conjunción con el Sol, la Luna puede pasar por delante del Sol visto desde una región estrecha en la superficie de la Tierra y causar un eclipse solar . En la luna llena , cuando la Luna está en oposición al Sol, la Luna puede pasar a través de la sombra de la Tierra, y un eclipse lunar es visible desde la mitad nocturna de la Tierra. La conjunción y la oposición de la Luna juntas tienen un nombre especial: sicigia ( del griego "unión"), debido a la importancia de estas fases lunares .
No se produce un eclipse en cada luna nueva o llena, porque el plano de la órbita de la Luna alrededor de la Tierra está inclinado con respecto al plano de la órbita de la Tierra alrededor del Sol (la eclíptica ): así que, visto desde la Tierra, cuando la Luna aparece más cerca del Sol (en luna nueva) o más lejos de él (en luna llena), los tres cuerpos normalmente no están exactamente en la misma línea.
Esta inclinación es en promedio de unos 5° 9′, mucho mayor que el diámetro medio aparente del Sol (32′ 2″), la Luna vista desde la superficie de la Tierra directamente debajo de la Luna (31′ 37″) y la sombra de la Tierra a la distancia lunar media (1° 23′).
Por lo tanto, en la mayoría de las lunas nuevas, la Tierra pasa demasiado al norte o al sur de la sombra lunar, y en la mayoría de las lunas llenas, la Luna no alcanza la sombra de la Tierra. Además, en la mayoría de los eclipses solares, el diámetro angular aparente de la Luna es insuficiente para ocluir completamente el disco solar, a menos que la Luna esté alrededor de su perigeo , es decir, más cerca de la Tierra y aparentemente más grande que el promedio. En cualquier caso, la alineación debe ser casi perfecta para provocar un eclipse.
Un eclipse puede ocurrir solamente cuando la Luna está en el plano de la órbita de la Tierra o cerca de él, es decir, cuando su latitud eclíptica es baja. Esto sucede cuando la Luna está alrededor de cualquiera de los dos nodos orbitales de la eclíptica en el momento de la sicigia . Por supuesto, para que se produzca un eclipse, el Sol también debe estar alrededor de un nodo en ese momento: el mismo nodo para un eclipse solar o el nodo opuesto para un eclipse lunar.
Recurrencias

Pueden ocurrir hasta tres eclipses durante una temporada de eclipses , un período de uno o dos meses que ocurre dos veces al año, alrededor del momento en que el Sol está cerca de los nodos de la órbita de la Luna.
Un eclipse no ocurre todos los meses, porque un mes después de un eclipse la geometría relativa del Sol, la Luna y la Tierra ha cambiado.
Visto desde la Tierra, el tiempo que tarda la Luna en volver a un nodo, el mes dracónico , es menor que el tiempo que tarda la Luna en volver a la misma longitud eclíptica que el Sol: el mes sinódico . La razón principal es que durante el tiempo que la Luna ha completado una órbita alrededor de la Tierra, la Tierra (y la Luna) han completado aproximadamente 1 ⁄ 13 de su órbita alrededor del Sol: la Luna tiene que compensar esto para volver a entrar en conjunción u oposición con el Sol. En segundo lugar, los nodos orbitales de la Luna precesan hacia el oeste en longitud eclíptica, completando un círculo completo en aproximadamente 18,60 años, por lo que un mes dracónico es más corto que un mes sideral . En total, la diferencia de período entre el mes sinódico y el dracónico es de casi 2+1 ⁄ 3 días. Asimismo, visto desde la Tierra, el Sol pasa por ambos nodos a medida que avanza por su trayectoria eclíptico. El período que tarda el Sol en volver a un nodo se denomina eclipse o año dracónico : unos 346,6201 días, lo que supone aproximadamente 1 ⁄ 20 años más corto que un año sideral debido a la precesión de los nodos.
Si se produce un eclipse solar en una luna nueva, que debe estar cerca de un nodo, entonces en la siguiente luna llena la Luna ya se encuentra más de un día más allá de su nodo opuesto, y puede o no pasar por encima de la sombra de la Tierra. En la siguiente luna nueva está aún más adelante del nodo, por lo que es menos probable que haya un eclipse solar en algún lugar de la Tierra. Para el mes siguiente, seguramente no habrá ningún evento.
Sin embargo, unas 5 o 6 lunaciones después, la luna nueva caerá cerca del nodo opuesto. En ese tiempo (medio año de eclipses) el Sol también se habrá movido al nodo opuesto, por lo que las circunstancias volverán a ser propicias para uno o más eclipses.
Periodicidad
La periodicidad de los eclipses solares es el intervalo entre dos eclipses solares cualesquiera en sucesión, que será de 1, 5 o 6 meses sinódicos . [2] Se calcula que la Tierra experimentará un número total de 11.898 eclipses solares entre 2000 a. C. y 3000 d. C. Un eclipse solar en particular se repetirá aproximadamente cada 18 años, 11 días y 8 horas (6.585,32 días) de período, pero no en la misma región geográfica. [3] Una región geográfica en particular experimentará un eclipse solar en particular en cada período de 54 años y 34 días. [2] Los eclipses solares totales son eventos raros, aunque ocurren en algún lugar de la Tierra cada 18 meses en promedio. [4]
Repetición de eclipses solares
Para que dos eclipses solares sean casi idénticos, la alineación geométrica de la Tierra, la Luna y el Sol, así como algunos parámetros de la órbita lunar, deben ser los mismos. Para que se repita un eclipse solar, deben repetirse los siguientes parámetros y criterios:
- La Luna debe estar en fase nueva.
- La longitud del perigeo o apogeo de la Luna debe ser la misma.
- La longitud del nodo ascendente o del nodo descendente debe ser la misma.
- La Tierra estará casi a la misma distancia del Sol, e inclinada respecto a él en casi la misma orientación.
Estas condiciones están relacionadas con los tres períodos del movimiento orbital de la Luna, a saber, el mes sinódico , el mes anomalístico y el mes dracónico , y con el año anomalístico . En otras palabras, un eclipse particular se repetirá solo si la Luna completará aproximadamente un número entero de períodos sinódico, dracónico y anomalístico y la geometría Tierra-Sol-Luna será casi idéntica. La Luna estará en el mismo nodo y a la misma distancia de la Tierra. Esto sucede después del período llamado saros . Gamma ( qué tan lejos está la Luna al norte o al sur de la eclíptica durante un eclipse) cambia monótonamente a lo largo de cualquier serie de saros. El cambio en gamma es mayor cuando la Tierra está cerca de su afelio (junio a julio) que cuando está cerca del perihelio (diciembre a enero). Cuando la Tierra está cerca de su distancia promedio (marzo a abril o septiembre a octubre), el cambio en gamma es promedio.
Repetición de eclipses lunares
Para que se repita un eclipse lunar, se debe repetir la alineación geométrica de la Luna, la Tierra y el Sol, así como algunos parámetros de la órbita lunar. Para que se repita un eclipse lunar, se deben repetir los siguientes parámetros y criterios:
- La Luna debe estar en fase llena.
- La longitud del perigeo o apogeo de la Luna debe ser la misma.
- La longitud del nodo ascendente o del nodo descendente debe ser la misma.
- La Tierra estará casi a la misma distancia del Sol, e inclinada respecto a él en casi la misma orientación.
Estas condiciones están relacionadas con los tres períodos del movimiento orbital de la Luna, a saber, el mes sinódico , el mes anomalístico y el mes dracónico . En otras palabras, un eclipse particular se repetirá solo si la Luna completará aproximadamente un número entero de períodos sinódicos, dracónicos y anomalísticos (223, 242 y 239) y la geometría Tierra-Sol-Luna será casi idéntica a ese eclipse. La Luna estará en el mismo nodo y a la misma distancia de la Tierra. Gamma cambia monótonamente a lo largo de cualquier serie de Saros . El cambio en gamma es mayor cuando la Tierra está cerca de su afelio (junio a julio) que cuando está cerca del perihelio (diciembre a enero). Cuando la Tierra está cerca de su distancia promedio (marzo a abril o septiembre a octubre), el cambio en gamma es promedio.
Los eclipses no ocurrirían todos los meses
Otro aspecto a tener en cuenta es que el movimiento de la Luna no es un círculo perfecto. Su órbita es claramente elíptica, por lo que la distancia lunar a la Tierra varía a lo largo del ciclo lunar. Esta distancia variable cambia el diámetro aparente de la Luna y, por lo tanto, influye en las probabilidades, la duración y el tipo (parcial, anular, total, mixto) de un eclipse. Este período orbital se denomina mes anomalístico y, junto con el mes sinódico, causa el llamado " ciclo de luna llena " de aproximadamente 14 lunaciones en los tiempos y apariencias de las lunas llenas (y nuevas). La Luna se mueve más rápido cuando está más cerca de la Tierra (cerca del perigeo) y más lento cuando está cerca del apogeo (la distancia más lejana), cambiando así periódicamente el tiempo de las sicigias en hasta 14 horas a cada lado (en relación con su tiempo medio), y haciendo que el diámetro angular lunar aparente aumente o disminuya en aproximadamente un 6%. Un ciclo de eclipse debe comprender cerca de un número entero de meses anomalísticos para funcionar bien en la predicción de eclipses.
Si la Tierra tuviera una órbita perfectamente circular centrada alrededor del Sol, y la órbita de la Luna también fuera perfectamente circular y centrada alrededor de la Tierra, y ambas órbitas fueran coplanares (en el mismo plano) entre sí, entonces ocurrirían dos eclipses cada mes lunar (29,53 días). Un eclipse lunar ocurriría en cada luna llena, un eclipse solar en cada luna nueva, y todos los eclipses solares serían del mismo tipo. De hecho, las distancias entre la Tierra y la Luna y la de la Tierra y el Sol varían porque tanto la Tierra como la Luna tienen órbitas elípticas. Además, ambas órbitas no están en el mismo plano. La órbita de la Luna está inclinada unos 5,14° con respecto a la órbita de la Tierra alrededor del Sol. Por lo tanto, la órbita de la Luna cruza la eclíptica en dos puntos o nodos. Si una Luna Nueva tiene lugar a unos 17° de un nodo, entonces un eclipse solar será visible desde algún lugar de la Tierra. [5] [6] [7]
A una velocidad angular media de 0,99° al día, el Sol tarda 34,5 días en cruzar la zona de eclipse de 34° de ancho centrada en cada nodo. Debido a que la órbita de la Luna con respecto al Sol tiene una duración media de 29,53 días, siempre habrá uno y posiblemente dos eclipses solares durante cada intervalo de 34,5 días cuando el Sol pase por las zonas de eclipse nodales. Estos períodos de tiempo se denominan temporadas de eclipses. [2] Ocurren dos o tres eclipses en cada temporada de eclipses. Durante la temporada de eclipses, la inclinación de la órbita de la Luna es baja, por lo que el Sol , la Luna y la Tierra se alinean lo suficientemente rectos (en sicigia ) para que se produzca un eclipse.
Valores numéricos
Estas son las duraciones de los distintos tipos de meses discutidos anteriormente (según las efemérides lunares ELP2000-85, válidas para la época J2000.0; tomadas de ( por ejemplo ) Meeus (1991)):
- SM = 29,530588853 días (mes sinódico) [8]
- DM = 27,212220817 días (mes dracónico) [9]
- AM = 27,55454988 días (mes anómalo) [10]
- EY = 346,620076 días (año del eclipse)
Obsérvese que hay tres puntos móviles principales: el Sol, la Luna y el nodo (ascendente); y que hay tres períodos principales, cuando cada uno de los tres pares posibles de puntos móviles se encuentran: el mes sinódico cuando la Luna regresa al Sol, el mes dracónico cuando la Luna regresa al nodo, y el año del eclipse cuando el Sol regresa al nodo. Estas tres relaciones bidireccionales no son independientes (es decir, tanto el mes sinódico como el año del eclipse dependen del movimiento aparente del Sol, tanto el mes dracónico como el año del eclipse dependen del movimiento de los nodos), y de hecho el año del eclipse puede describirse como el período de compás de los meses sinódico y dracónico (es decir, el período de la diferencia entre los meses sinódico y dracónico); en la fórmula:
como se puede comprobar rellenando los valores numéricos indicados anteriormente.
Los ciclos de eclipses tienen un período en el que un cierto número de meses sinódicos es casi igual a un número entero o medio entero de meses dracónicos: uno de esos períodos después de un eclipse, una sicigia ( luna nueva o luna llena ) tiene lugar nuevamente cerca de un nodo de la órbita de la Luna en la eclíptica , y un eclipse puede ocurrir nuevamente. Sin embargo, los meses sinódicos y dracónicos son inconmensurables: su razón no es un número entero. Necesitamos aproximar esta razón por fracciones comunes : los numeradores y denominadores dan entonces los múltiplos de los dos períodos (meses dracónicos y sinódicos) que (aproximadamente) abarcan la misma cantidad de tiempo, lo que representa un ciclo de eclipses.
Estas fracciones se pueden encontrar mediante el método de fracciones continuas : esta técnica aritmética proporciona una serie de aproximaciones progresivamente mejores de cualquier valor numérico real mediante fracciones propias.
Dado que puede haber un eclipse cada medio mes dracónico, necesitamos encontrar aproximaciones para el número de medios meses dracónicos por mes sinódico: por lo que la relación objetivo para aproximar es: SM / (DM/2) = 29,530588853 / (27,212220817/2) = 2,170391682
La expansión de fracciones continuas para esta relación es:
2.170391682 = [2;5,1,6,1,1,1,1,1,11,1,...]: [11]Cocientes convergentes medio ciclo decimal DM/SM nombrado (si lo hay) 2; 2/1 = 2 meses sinódicos 5 11/5 = 2,2 pentaluminio 1 13/6 = 2,166666667 semestre 6 89/41 = 2,170731707 heptones 1 102/47 = 2,170212766 octones 1 191/88 = 2.170454545 tzolkinex 1 293/135 = 2.170370370 tritos 1 484/223 = 2.170403587 saros 1 777/358 = 2.170391061 inex 11 9031/4161 = 2,170391732 bits de selección 1 9808/4519 = 2,170391679 años cuadrados ...
La relación de meses sinódicos por medio año de eclipse produce la misma serie:
5.868831091 = [5;1,6,1,1,1,1,1,11,1,...]Cocientes convergentes SM/mitad EY decimal SM/ciclo con nombre EY completo 5; 5/1 = 5 pentaluminio 1 6/1 = 6 12/1 semestre 6 41/7 = 5,857142857 heptones 1 47/8 = 5,875 47/4 octón 1 88/15 = 5.866666667 tzolkinex 1 135/23 = 5.869565217 tritos 1 223/38 = 5.868421053 223/19 saros 1 358/61 = 5.868852459 716/61 inex 11 4161/709 = 5,868829337 bits de selección 1 4519/770 = 5,868831169 4519/385 año cuadrado ...
Cada uno de ellos es un ciclo de eclipse. Se pueden construir ciclos menos precisos mediante combinaciones de estos.
Ciclos de eclipses
Esta tabla resume las características de varios ciclos de eclipses y puede calcularse a partir de los resultados numéricos de los párrafos anteriores; cf. Meeus (1997) Cap. 9. Se dan más detalles en los comentarios que aparecen a continuación y varios ciclos notables tienen sus propias páginas. Se han señalado muchos otros ciclos, algunos de los cuales han recibido nombre. [3]
El número de días indicado es el promedio. El número real de días y fracciones de días entre dos eclipses varía debido a la variación en la velocidad de la Luna y del Sol en el cielo. La variación es menor si el número de meses anómalos está cerca de un número entero, y si el número de años anómalos está cerca de un número entero. (Véase los gráficos más abajo del semestre y del ciclo hipárquico).
Cualquier ciclo de eclipse, y de hecho el intervalo entre dos eclipses, se puede expresar como una combinación de intervalos saros ( s ) e inex ( i ). Estos se enumeran en la columna "fórmula".
| Ciclo | Fórmula | Días | Meses sinódicos | Meses draconianos | Meses anómalos | Años de eclipse | Años julianos | Años anómalos | Temporadas de eclipses | Nodo |
|---|---|---|---|---|---|---|---|---|---|---|
| quincena | 19 yo − 30+1 ⁄ 2 segundo | 14,77 | 0,5 | 0,543 | 0,536 | 0,043 | 0.040 | 0.040 | 0,086 | alternar |
| mes sinódico | 38 yo − 61 s | 29,53 | 1 | 1.085 | 1.072 | 0,085 | 0,081 | 0,081 | 0,17 | mismo |
| pentalux | 53 s − 33 i | 147,65 | 5 | 5.426 | 5.359 | 0,426 | 0,404 | 0,404 | 0,852 | alternar |
| semestre | 5 yo - 8 s | 177,18 | 6 | 6.511 | 6.430 | 0,511 | 0,485 | 0,485 | 1 | alternar |
| año lunar | 10 yo - 16 s | 354.37 | 12 | 13.022 | 12.861 | 1.022 | 0,970 | 0,970 | 2 | mismo |
| hexón | 13 s - 8 i | 1.033,57 | 35 | 37.982 | 37.510 | 2.982 | 2.830 | 2.830 | 6 | mismo |
| heptón | 5 s - 3 yo | 1.210,75 | 41 | 44.493 | 43.940 | 3.493 | 3.315 | 3.315 | 7 | alternar |
| Octón | 2 yo - 3 s | 1.387,94 | 47 | 51.004 | 50.371 | 4.004 | 3.800 | 3.800 | 8 | mismo |
| Tzolkinex | 2 s − yo | 2.598,69 | 88 | 95.497 | 94.311 | 7.497 | 7.115 | 7.115 | 15 | alternar |
| Hibbardina | 31 s - 19 i | 3.277,90 | 111 | 120.457 | 118.960 | 9.457 | 8.974 | 8.974 | 19 | alternar |
| sar (medio saros) | 1 ⁄ 2 segundo | 3.292,66 | 111.5 | 120.999 | 119.496 | 9.499 | 9.015 | 9.015 | 19 | mismo |
| Tritos | yo - s | 3.986,63 | 135 | 146.501 | 144.681 | 11.501 | 10.915 | 10.915 | 23 | alternar |
| saros ( s ) | s | 6.585,32 | 223 | 241.999 | 238.992 | 18.999 | 18.030 | 18.029 | 38 | mismo |
| Ciclo metónico | 10 yo - 15 s | 6.939,69 | 235 | 255.021 | 251.853 | 20.021 | 19.000 | 18.999 | 40 | mismo |
| semanex | 3 s - yo | 9,184.01 | 311 | 337.496 | 333.303 | 26.496 | 25.145 | 25.144 | 53 | alternar |
| esto | 4 y 5 segundos | 9.361,20 | 317 | 344.007 | 339.733 | 27.007 | 25.630 | 25.629 | 54 | mismo |
| inex ( yo ) | i | 10.571,95 | 358 | 388.500 | 383.674 | 30.500 | 28.944 | 28.944 | 61 | alternar |
| exégesis | 3 segundos | 19.755,96 | 669 | 725.996 | 716.976 | 56.996 | 54.089 | 54.087 | 114 | mismo |
| Ciclo de Aubrey | yo + 1 ⁄ 2 s | 20.449,93 | 692.5 | 751.498 | 742.162 | 58.998 | 55.989 | 55.987 | 118 | alternar |
| Unidos | yo + 2 s | 23.742,59 | 804 | 872.497 | 861.658 | 68.497 | 65.004 | 65.002 | 137 | alternar |
| Ciclo calipico | 40 yo − 60 s | 27.758,75 | 940 | 1020.084 | 1007.411 | 80.084 | 75.999 | 75.997 | 160 | mismo |
| tríada | 3 yo | 31.715,85 | 1074 | 1165.500 | 1151.021 | 91.500 | 86.833 | 86.831 | 183 | alternar |
| Cuarto de ciclo de Palmen | 4 yo - 1 s | 35.702,48 | 1209 | 1312.002 | 1295.702 | 103.002 | 97.748 | 97.745 | 206 | mismo |
| Ciclo del mercurio | 2 yo + 3 s | 40.899,87 | 1385 | 1502.996 | 1484.323 | 117.996 | 111.978 | 111.975 | 236 | mismo |
| Tritrix | 3 yo + 3 s | 51.471,82 | 1743 | 1891.496 | 1867.997 | 148.496 | 140.922 | 140.918 | 297 | alternar |
| Ciclo de la Hire | 6 yo | 63.431,70 | 2148 | 2331.001 | 2302.041 | 183.001 | 173.667 | 173.662 | 366 | mismo |
| trihex | 3 yo + 6 s | 71.227,78 | 2412 | 2617.492 | 2584.973 | 205.492 | 195.011 | 195.006 | 411 | alternar |
| Ciclo Lambert II | 9 yo + s | 101.732,88 | 3445 | 3738.500 | 3692.054 | 293.500 | 278.529 | 278.522 | 587 | alternar |
| Ciclo de Macdonald | 6 yo + 7 s | 109.528,95 | 3709 | 4024.991 | 3974.986 | 315.991 | 299.874 | 299.866 | 632 | mismo |
| Ciclo de Utting | 10 yo + s | 112.304,83 | 3803 | 4127.000 | 4075.727 | 324.000 | 307.474 | 307.466 | 648 | mismo |
| seleccionar | 11 yo + s | 122.876,78 | 4161 | 4515.500 | 4459.401 | 354.500 | 336.418 | 336.409 | 709 | alternar |
| Ciclo de Hiparco | 25 yo − 21 s | 126.007,02 | 4267 | 4630.531 | 4573.002 | 363.531 | 344.988 | 344.979 | 727 | alternar |
| Año cuadrado | 12 yo + s | 133.448,73 | 4519 | 4904.000 | 4843.074 | 385.000 | 365.363 | 365.353 | 770 | mismo |
| Gregoriana | 6 yo + 11 s | 135.870,24 | 4601 | 4992.986 | 4930.955 | 391.986 | 371.992 | 371.983 | 784 | mismo |
| hexdodeca | 6 yo + 12 s | 142.455,56 | 4824 | 5234.985 | 5169.947 | 410.985 | 390.022 | 390.012 | 822 | mismo |
| Ciclo de Guinness de Grattan | 12 yo - 4 s | 142.809,92 | 4836 | 5248.007 | 5182.807 | 412.007 | 390.992 | 390.982 | 824 | mismo |
| Hiparquiano | 14 yo + 2 s | 161.177,95 | 5458 | 5922.999 | 5849.413 | 464.999 | 441.281 | 441.270 | 930 | mismo |
| Periodo básico | 18 yo | 190.295,11 | 6444 | 6993.002 | 6906.123 | 549.002 | 521.000 | 520.986 | 1098 | mismo |
| Chalepe | 18 yo + 2 s | 203.465,76 | 6890 | 7476.999 | 7.384.107 | 586.999 | 557.059 | 557.044 | 1174 | mismo |
| Tetradia (Meeus III) | 22 yo - 4 s | 206.241,63 | 6984 | 7579.008 | 7484.849 | 595.008 | 564.659 | 564.644 | 1190 | mismo |
| Tetradia (Meeus I) | 19 yo + 2 s | 214.037,71 | 7248 | 7865.499 | 7767.781 | 617.499 | 586.003 | 585.988 | 1235 | alternar |
| hiper exeligmos | 24 yo + 12 s | 332.750,68 | 11268 | 12227.987 | 12076.070 | 959.987 | 911.022 | 910.998 | 1920 | mismo |
| cartucho | 52 yo | 549.741,44 | 18616 | 20202.006 | 19951.022 | 1586.006 | 1505.110 | 1505.070 | 3172 | mismo |
| Palea-Relojería | 55 yo + 3 s | 601.213,26 | 20359 | 22093.502 | 21819.019 | 1734.502 | 1646.032 | 1645.989 | 3469 | alternar |
| hibrida | 55 yo + 4 s | 607.798,58 | 20582 | 22335.501 | 22058.012 | 1753.501 | 1664.062 | 1664.018 | 3507 | alternar |
| Selenidia 1 | 55 yo + 5 s | 614.383,90 | 20805 | 22577.499 | 22297.004 | 1772.499 | 1682.091 | 1682.047 | 3545 | alternar |
| Próxima | 58 yo + 5 s | 646.099,75 | 21879 | 23743.000 | 23448.024 | 1864.000 | 1768.925 | 1768.878 | 3728 | mismo |
| heliotropo | 58 yo + 6 s | 652.685,07 | 22102 | 23984.998 | 23687.016 | 1882.998 | 1786.954 | 1786.907 | 3766 | mismo |
| Megalosaros | 58 yo + 7 s | 659.270,40 | 22325 | 24226.997 | 23926.009 | 1901.997 | 1804.984 | 1804.936 | 3804 | mismo |
| inmobilis | 58 yo + 8 s | 665.855,72 | 22548 | 24468.996 | 24165.001 | 1920.996 | 1823.014 | 1822.966 | 3842 | mismo |
| Precisión extrema | 58 yo + 9 s | 672.441,04 | 22771 | 24710.994 | 24403.993 | 1939.994 | 1841.043 | 1840.995 | 3880 | alternar |
| Ciclo de Mackay | 76 yo + 9 s | 862736.15 | 29215 | 31703.996 | 31310.116 | 2488.996 | 2362.043 | 2361.981 | 4978 | alternar |
| Selenidia 2 | 95 yo + 11 s | 1.076.773,86 | 36463 | 39569.496 | 39077.897 | 3106.496 | 2948.046 | 2947.968 | 6213 | alternar |
| Relojería | 110 yo + 7 s | 1.209.011,84 | 40941 | 44429.003 | 43877.031 | 3488.003 | 3310.094 | 3310.007 | 6976 | mismo |
Notas
- Quincena
- Medio mes sinódico (29,53 días). Cuando hay un eclipse, hay una buena probabilidad de que en la siguiente sicigia haya otro eclipse: el Sol y la Luna se habrán movido unos 15° con respecto a los nodos (la Luna está opuesta a donde estaba la vez anterior), pero las luminarias todavía pueden estar dentro de los límites para hacer un eclipse. Por ejemplo, el eclipse lunar penumbral del 26 de mayo de 2002 es seguido por el eclipse solar anular del 10 de junio de 2002 y el eclipse lunar penumbral del 24 de junio de 2002. La quincena lunar más corta entre una luna nueva y una luna llena dura solo unos 13 días y 21,5 horas, mientras que la quincena lunar más larga de este tipo dura unos 15 días y 14,5 horas. (Debido a la evasión , estos valores son diferentes de un cuarto de luna a otro. La quincena lunar más corta entre el primer y el último cuarto de luna dura solo unos 13 días y 12 horas, mientras que la más larga dura unos 16 días y 2 horas).
- Para obtener más información, consulte temporada de eclipses .
- Mes sinódico
- De manera similar, dos eventos con un mes sinódico de diferencia tienen al Sol y a la Luna en dos posiciones a cada lado del nodo, a 29° de distancia: ambos pueden causar un eclipse solar parcial. En el caso de un eclipse lunar, se trata de un eclipse lunar penumbral.
- Pentalunex
- 5 meses sinódicos. Los eclipses solares o lunares sucesivos pueden ocurrir con 1, 5 o 6 meses sinódicos de diferencia. [3] Cuando dos eclipses solares están separados por un mes, uno se verá cerca del Círculo Polar Ártico y el otro cerca del Círculo Antártico . Cuando están separados por cinco meses, ambos se verán cerca del Círculo Polar Ártico o ambos cerca del Círculo Antártico.
- Semestre
- Medio año lunar. Los eclipses se repetirán exactamente con un semestre de diferencia en nodos alternos en un ciclo que dura 8 o 9 eclipses. Debido a que está cerca de la mitad de un entero de meses anomalísticos, dracónicos y años tropicales, cada eclipse solar (normalmente) alternará entre hemisferios cada semestre, así como entre total y anular. Por lo tanto, normalmente hay un máximo de un eclipse total o anular cada uno en un año lunar determinado. (Sin embargo, en medio de una serie de ocho semestres, los hemisferios cambian, y hay un cambio durante la serie entre si los impares o los pares son totales). Es posible tener dos eclipses separados por un semestre y un tercer eclipse un mes antes o después, de modo que dos de los tres estén separados por siete meses, pero esto solo sucede durante ciertos siglos (ver gráfico de inex versus fecha a continuación). Debido a que está cerca de un medio entero de meses anomalísticos, dracónicos y años tropicales, cada eclipse lunar generalmente alternará entre los bordes de la sombra de la Tierra cada semestre, así como también alternará entre eclipses lunares con la diferencia de sombra penumbral y umbral de la Luna menor o mayor que 1. Por lo tanto, generalmente hay un máximo de un eclipse lunar con la diferencia de sombra penumbral y umbral de la Luna menor o mayor que 1 cada uno en un año lunar determinado.
- Año lunar
- Doce meses (sinódicos), un poco más largo que un año de eclipse: el Sol ha regresado al nodo, por lo que pueden volver a ocurrir eclipses:
- Hexón
- 6 estaciones de eclipses y un ciclo de eclipses bastante corto. Cada eclipse en una serie de hexones (excepto el último) es seguido por un eclipse cuyo número de serie de saros es 8 veces menor, y siempre ocurre en el mismo nodo. Es igual a 35 meses sinódicos, 1 menos que 3 años lunares (36 meses sinódicos). En cualquier momento dado hay seis series de hexones activas.
- Heptón
- 7 estaciones de eclipses y uno de los ciclos de eclipses menos destacables. Cada eclipse en un heptón es seguido por un eclipse 3 series de saros antes, que siempre ocurre en nodos alternos. Es igual a 41 meses sinódicos. El intervalo es casi un número entero de semanas (172,96), por lo que cada eclipse es seguido por otro que suele ocurrir el mismo día de la semana (retrocediendo irregularmente en un promedio de un cuarto de día). En cualquier momento dado hay siete series de heptones activas.
- Octón
- 8 temporadas de eclipses, 1 ⁄ 5 del ciclo metónico y un ciclo de eclipses corto bastante decente, pero pobre en retornos anómalos. Cada octón de una serie está separado por 2 saros y siempre ocurre en el mismo nodo. Es igual a 47 meses sinódicos. En cualquier momento dado hay ocho series de octones activas.
- Tzolkinex
- Incluye medio mes dracónico, por lo que ocurre en nodos alternos y se alterna entre hemisferios. Cada eclipse consecutivo es miembro de la serie de saros que precede al anterior. Equivale a casi diez tzolk'ins . Cada tercer tzolkinex en una serie está cerca de un número entero de meses anómalos y, por lo tanto, tendrá propiedades similares.
- Hibbardina
- Un "ciclo" de eclipses de 3 eclipses como máximo, pero que en realidad se entiende como un período que separa un par de eclipses similares con valores gamma opuestos. Si se añade 1 lunación (para 112 meses sinódicos) se obtiene otro período con la misma propiedad, la otra mitad de un saros. Los dos rodean un sar (medio saros). Se llama así por William B. Hibbard, quien lo identificó en 1956. [3] Un año lunar menos que una Hibbardina, 99 lunaciones, es solo alrededor de un día y medio más que ocho años.
- Sar (medio saros)
- Incluye un número impar de quincenas (223). Como resultado, los eclipses lunares y solares se alternan en cada ciclo, y ocurren en el mismo nodo y con características similares. Un eclipse solar con una pequeña gamma será seguido por un eclipse lunar total muy central. Un eclipse solar en el que la penumbra de la Luna apenas roza el borde sur de la Tierra será seguido medio saros más tarde por un eclipse lunar en el que la Luna apenas roza el borde sur de la penumbra de la Tierra. [3]
- Tritos
- Equivale a un inex menos un saros. Un triple tritos se acerca a un número entero de meses anómalos y, por lo tanto, tendrá propiedades similares.
- Saros
- El ciclo de eclipses más conocido (descrito en el Almagesto pero al que no se le da este nombre) y uno de los mejores para predecir eclipses, en el que 223 meses sinódicos equivalen a 242 meses dracónicos con un error de solo 51 minutos. También está muy cerca de 239 meses anomalísticos, lo que hace que las circunstancias entre dos eclipses separados por un saros sean muy similares. Al ser un tercio de día más que un número entero de días, cada eclipse sucesivo está centrado unos 120° más al oeste sobre la Tierra. Si la órbita de la Tierra alrededor del Sol fuera circular, el ciclo de saros estaría muy cerca de una órbita periódica que se repetiría exactamente cada 223 meses.ὤ [12]

- Ciclo metónico o eneadecaeteris
- Casi 6940 días, pero como ciclo de eclipses se puede considerar como 235 meses sinódicos. Esto es sólo una hora y media menos que 19 años de 365+1 ⁄ 4 días. También son 5 períodos "octón" y cerca de 20 años de eclipse, por lo que da una serie corta de cuatro o cinco eclipses en la misma fecha del calendario o en dos fechas del calendario. Equivale a 110 "meses huecos" de 29 días y 125 "meses completos" de 30 días.
- Semanex
- Equivale a un número entero de semanas más una centésima de día, por lo que los eclipses consecutivos del ciclo suelen coincidir en el mismo día de la semana. Cada eclipse de este período es miembro de una serie de saros anterior, que siempre se produce en nodos alternos. [3]
- Tix
- Este ciclo de eclipses dura algo más de 36 tzolk'ins y 317 lunaciones. Cada eclipse de este período es seguido por otro eclipse 4 series de saros después, que siempre ocurren en el mismo nodo. [3]
- Inex
- Muy conveniente en la clasificación de los ciclos de eclipses. Un inex después de un eclipse, otro eclipse tiene lugar en la latitud opuesta. Las series de inex, después de un comienzo intermitente, continúan durante muchos miles de años dando lugar a eclipses cada 29 años menos 20 días, o 21 días si el último año tiene 366 días. Dieciocho ciclos de inex (ver "Período básico") son iguales a 520,9996 años julianos, por lo que un inex es 28+17/18Años julianos . El ciclo inex es el ciclo que produce el mayor número de eclipses mientras dura. La serie inex 30 produjo por primera vez un eclipse solar en la serie saros -245 (en 9435 a. C.), ha estado produciendo eclipses cada 29 años desde la serie saros -197 (en 8045 a. C.), y continuará haciéndolo mucho después del año 15 000 d. C. [13], momento en el que habrá producido 707 eclipses consecutivos. El nombre fue introducido por George van den Bergh en 1951. [3]
- Exeligmos
- Un triple saros, con la ventaja de que tiene casi un número entero de días, por lo que el siguiente eclipse será visible en lugares cercanos al eclipse que ocurrió un exeligmos antes, en contraste con el saros, en el que el eclipse ocurre unas 8 horas más tarde en el día o unos 120° al oeste del eclipse que ocurrió un saros antes. Ptolomeo en el Almagesto lo menciona después de discutir lo que ahora llamamos el saros, y dice que se llama el exeligmos (ἐξελιγμός, que significa "desenrollado").
- Ciclo de Aubrey
- Recibe su nombre por el cálculo de los eclipses medidos con los agujeros de Aubrey , ubicados en Stonehenge . Con 1385 quincenas, los eclipses lunares y solares se alternan en 56 años menos 3,5 días. [3]
- Unidos
- Muy cerca de 65 años. Equivale a 67 años lunares y supera a 65 años julianos por solo 1,3 días (1,8 días sobre 65 años gregorianos promedio). Nombre sugerido por Karl Palmen en el que se suman 2 saros sobre un inex. [3] Un período de tres Unidos (195 años, un "Trihex") está bastante cerca tanto de un número entero de años anomalísticos como de un número entero de meses anomalísticos, lo que significa que el intervalo entre dos eclipses es bastante constante.
- Ciclo calipico
- Originalmente definido como 4 ciclos metónicos menos un día o exactamente 76 años de 365+1 ⁄ 4 días. En la tabla, tomados como 940 meses sinódicos, equivalen a 441 meses huecos y 499 meses completos. Este ciclo, aunque útil por ejemplo en el cálculo de la fecha de Pascua , puede producir como máximo dos eclipses solares (ambos parciales) y como máximo dos eclipses lunares (ambos penumbrales). El ciclo calípico es de 20 octones, y las series de octones a menudo producen solo 21 eclipses, por lo que solo el primero y el último de una serie de este tipo están separados por un ciclo calípico. La mayoría de los eclipses no son seguidos por otro eclipse 940 lunaciones después, sino 939 lunaciones después (dos inex y un saros), lo que se acerca a un número entero de meses dracónicos, produciendo eclipses similares. Esto se llama un período calípico corto. [3]
- Tríada
- Un triple inex, con la ventaja de que tiene casi un número entero de meses anomalísticos, lo que hace que las circunstancias entre dos eclipses separados por una tríada sean muy similares, pero en latitudes opuestas. Casi exactamente 87 años calendario menos 2 meses. La tríada significa que cada tercera serie de saros será similar (eclipses centrales mayoritariamente totales o mayoritariamente anulares, por ejemplo). Los saros solares 130 , 133 , 136 , 139 , 142 y 145 , por ejemplo, todos producen eclipses principalmente totales cuando son centrales, porque la luna está cerca del perigeo. De hecho, el eclipse solar del 17 de octubre de 1781, que estaba en la serie de saros 130 e inex 50, fue muy central y en perigeo. [12] Pero esta repetición no es perfecta. Dentro de unos 2460 años, la serie antes mencionada, 130, 133... (equivalente a 1 módulo 3) dará eclipses solares centrales anulares, próximos al apogeo. Dentro de unos 820 años, los eclipses lunares centrales, pero no los solares, estarán cerca del perigeo cada tres series de saros, y dentro de unos 1640 años la serie solar de saros con índice equivalente a 2 módulo 3 dará eclipses centrales cercanos al perigeo. [14]
- Ciclo del Cuarto de Palmen
- Recibe su nombre en honor a Karl Palmen, ya que a 4 inex se le resta un saros. A cada eclipse le sigue una serie de eclipses de 4 saros más tarde, que siempre ocurren en el mismo nodo. Equivale a 97 años y 9 meses o 1209 lunaciones. [3]
- Ciclo del mercurio
- Equivale aproximadamente a 353 períodos sinódicos de Mercurio , [15] de modo que los eclipses se sincronizan con el momento de la posición de Mercurio en su órbita durante cada período, lo que equivale a 112 años menos una semana o 1385 lunaciones. [3]
- Tritrix
- Es igual a 3 inex más 3 saros, que son 140 años 11 meses o 1743 lunaciones, siempre ocurriendo en nodos alternados. [3] El tritrix está muy cerca de un número entero de meses anomalísticos ((1867.9970) y cerca de un número entero de años anomalísticos, lo que significa que el intervalo entre dos eclipses es bastante constante. Dos tritrix menos un saros (3263 lunaciones) está aún más cerca de un número entero de meses anomalísticos (3497.0018), siendo exactamente trece diecisieteavos del Ciclo de Hiparco (ver abajo).
- Ciclo de la Hire
- Un inex séxtuple, adoptado por Phillippe de la Hire en su Tabularum Astronomicarum en 1687. Equivale a 6 períodos inex, lo que equivale a 173 años y alrededor de 8 meses, o 2148 lunaciones, que equivalen a 179 años lunares, y siempre ocurren en el mismo nodo en casi un número entero de meses anomalísticos, ya que equivale a 2 tríadas. [3]
- Trihex
- Equivale a 3 inex más 6 saros, con una duración de 195 años julianos y 4 días o 2412 lunaciones, lo que equivale a 201 años lunares, y siempre se produce en nodos alternos. Sólo dos días en un número entero de años anomalísticos y cerca de un número entero de meses anomalísticos, lo que significa que el intervalo entre dos eclipses es bastante constante.
- Ciclo Lambert II
- Ciclo de eclipses en el que los eclipses ocurren en circunstancias similares, según Johann Heinrich Lambert en 1765. (El "ciclo Lambert I" es lo que también llamamos el inex.) Muy cercano a un número medio entero de meses dracónicos. Equivale a unos 278 años y medio. [3]
- Ciclo de Macdonald
- Un ciclo de eclipses de una duración de 299 años y unos diez meses y medio, que se produce siempre en el mismo nodo. Peter Macdonald descubrió que una serie de eclipses de duración especialmente larga visibles desde Gran Bretaña se produce con este intervalo en el período comprendido entre el año 1 y el 3000 d. C. [3] Una serie de Macdonald tiene alrededor de diez eclipses y dura unos 3000 años. Todos o la mayoría tienen lugar el mismo día de la semana, ya que el intervalo es solo una hora menos que un número entero de semanas y la duración es bastante constante porque la anomalía de la luna es casi constante.
- Ciclo de Utting
- El séptimo convergente en el desarrollo de fracciones continuas entre la relación del año del eclipse y el mes sinódico, si esta relación se aproxima a entre 2,17039173 y 2,17039179. Discutido por James Utting en 1827. [3]
- Selebit
- Un ciclo de eclipses en el que el número de años de eclipse (354,5) coincide (por casualidad) con el número de días de un año lunar (354,371). Equivale aproximadamente a 336 años, 5 meses y 6 días o 4161 lunaciones. Es un convergente en el desarrollo de fracciones continuas de la relación entre el año de eclipse y el mes sinódico, lo que da a una serie de eclipses separados por un selebit una esperanza de vida de miles de años.
- Ciclo de Hiparco
- No es un ciclo de eclipses de larga duración, pero Hiparco lo construyó para que coincidiera con un número entero de meses, años y días sinódicos y anomalísticos (345). Debido a que está cerca de un número entero tanto de meses como de años anomalísticos, su duración siempre está dentro de una hora de 126007 días y media hora. (Véanse los gráficos más abajo del ciclo semestral y de Hiparco). Esto significa que en el momento del segundo eclipse el mismo lado de la Tierra estará de cara al Sol que en el primer eclipse (pero el valor de gamma será diferente). Al comparar sus propias observaciones de eclipses con los registros babilónicos de 345 años antes, Hiparco pudo verificar la precisión de los diversos períodos que usaban los caldeos. Ptolomeo señala que dividirlo por 17 todavía da un número entero de meses sinódicos (251) y meses anomalísticos (269), pero esto no es un intervalo de eclipse porque no está cerca de un número entero o medio entero de meses dracónicos.
- Año cuadrado
- Ciclo de eclipses en el que el número de años solares (365,371) coincide (por casualidad) con el número de días de un año solar (365,242). Dura 365 años y 4,5 meses o 4519 lunaciones. Es el octavo convergente en el desarrollo de fracciones continuas de la relación entre el año de eclipse y el mes sinódico, lo que da a una serie de eclipses separados por un año cuadrado una esperanza de vida de miles de años. Muchos eclipses de nuestros días pertenecen a series de "años cuadrados" o series de selebit que se han estado produciendo durante más de 13.000 años, y muchos continuarán durante más de 13.000 años. [13] [3]
- Gregoriana
- Conocido por regresar hacia el mismo día de la semana y fecha del calendario gregoriano, a medida que se logra un número entero de años, meses y semanas, generalmente moviéndose solo un cuarto de día más tarde en el calendario gregoriano. [3] [16]
- Hexdodeka
- Equivale a seis unidos o dos trihex. Útil para realizar cálculos precisos de la cronología de las sicigias lunisolares. [3]
- Ciclo de Guinness de Grattan
- El ciclo más corto que da eclipses en la misma fecha (más o menos) tanto en el calendario gregoriano como en un calendario lunar de 12 meses, porque es casi exactamente un número entero de años gregorianos (391.00029) además de ser exactamente 403 años lunares de 12 meses. Descubierto por Henry Grattan Guinness en una interpretación especulativa de Apocalipsis 9:15. [17] [3]
- Hiparquiano
- Catorce inex más dos saros. El Almagesto atribuye este ciclo a Hiparco . George van den Bergh lo llamó el "Período Babilónico Largo" o el "Período Babilónico Antiguo", pero no hay evidencia de que los babilonios estuvieran al tanto de él. [3]
- Periodo básico
- Alcanza casi un número entero (521) de años julianos , años anomalísticos (521 años anomalísticos menos 5 días) y semanas (27185 semanas más 0,1 días), lo que da lugar a eclipses en el mismo día del calendario juliano y semana. [3]
- Chalepe
- Equivale a 18 inex más 2 saros, por lo tanto 557 años más aproximadamente 1 mes. [3]

- Tetradia
- A veces ocurren 4 eclipses lunares totales seguidos con intervalos de 6 lunaciones (un semestre) entre ellos, y esto se llama tétrada . Giovanni Schiaparelli notó que hay eras en las que tales tétradas ocurren con relativa frecuencia, interrumpidas por eras en las que son raras. Esta variación toma alrededor de 6 siglos. Antonie Pannekoek (1951) ofreció una explicación para este fenómeno y encontró un período de 591 años. Van den Bergh (1954) a partir del Canon der Finsternisse de Theodor von Oppolzer encontró un período de 586 años. Esto resulta ser un ciclo de eclipses; véase Meeus [I] (1997). El fenómeno está relacionado con la órbita elíptica de la Tierra, como se explica a continuación. Recientemente, Tudor Hughes explicó que los cambios seculares en la excentricidad de la órbita de la Tierra hacen que el período de ocurrencia de tétradas sea variable, y actualmente es de alrededor de 565 años; véase Meeus III (2004) para una discusión detallada. El período Tetradia también aparece en la distancia entre eras en las que hay pares de eclipses (no consecutivos) con siete meses de diferencia, o eras en las que hay más pares de eclipses con un mes de diferencia, o eras en las que hay series de saros en las que gamma es bastante constante durante muchas décadas, o eras con más eclipses de gamma baja. [14]
- Hiper exeligmos
- Equivale a 12 "Períodos Calípicos Cortos" (cada uno un mes más corto que un ciclo Calípico), o 12 ciclos Calípicos menos 1 año lunar, por lo tanto un poco más de 911 años o 11268 lunaciones, que son 939 años lunares. Mencionado por primera vez por Alexander Pogo en 1935. [3]
Los nueve ciclos siguientes, desde Cartouche hasta Accuratissima, son todos similares, ya que equivalen a 52 períodos inex, más hasta dos tríadas y varias cantidades de períodos saros. Esto significa que todos tienen un número casi entero de meses anómalos. Su duración va de 1505 a 1841 años y cada serie dura muchos miles de años.
- Cartucho
- Equivale a 52 inex, es decir, 1505 años y entre 1 y 2 meses. Los eclipses en este período ocurren a una distancia similar, ya que se alcanza un número casi entero de meses anomalísticos. [3]
- Palea-Relojería
- Equivale a 55 inex más 3 saros, lo que equivale a más de 1646 años. Resulta útil para calcular el tiempo de los eclipses. Es casi un número entero de meses anómalos. Una serie dura decenas de miles de años. [3]
- hibrida
- Equivale a 55 inex más 4 saros, un saros más que una Palaea-Horologia, por lo tanto más de 1664 años, cerca de un número entero de meses anomalísticos, por lo tanto con propiedades similares, pero en latitud opuesta. [3]
- Selenidium
- Un saros más que un Hybridia. Nombre de los ciclos de eclipses útil para calcular las magnitudes de los eclipses en el tercer milenio . George van den Bergh mencionó por primera vez un período de 55 inex más 5 saros (durante 1682 años) antes de mencionar un período de 95 inex más 11 saros (durante 2948 años) en 1951. [3]
- Próxima
- Equivale a 58 inex más 5 saros, por lo tanto un poco menos de 1769 años, ocurriendo siempre en el mismo nodo y hacia un número entero de meses y semanas dracónicos y anomalísticos, haciendo que las circunstancias de cada eclipse próximo aparte sean similares en carácter. [3]
- Heliotropo
- Equivale a 58 inex más 6 saros, un saros más que Próxima, por lo tanto unos 1787 años. Útil para calcular las posiciones longitudinales de las líneas centrales de los eclipses en la superficie de la Tierra cerca de un número entero de años (1786,954 años julianos, 1786,991 gregorianos). [3]
- Megalosaros
- Equivale a 58 inex más 7 saros (un saros más que un heliotropo), lo que equivale a 95 ciclos metónicos, o 95 saros más 95 años lunares, o 100 saros más 25 lunaciones, o un poco más de 1805 años, siempre ocurriendo en el mismo nodo, y revelando el desajuste del ciclo metónico de 19 años ya que 95 repeticiones acumulan el desajuste a unos tres años. Las 25 lunaciones adicionales son necesarias porque 100 ciclos saros exceden la expectativa de vida de una serie saros. [3] [18]
- Inmobiliaria
- Equivale a 58 inex más 8 saros (un saros más que un Megalosaros), lo que equivale exactamente a 1879 años lunares. Siempre ocurre en el mismo nodo. Muy cerca de un número entero de meses anomalísticos, aunque 43 inex menos 5 saros (14279 meses, 1154,5 años) está aún más cerca. [3]
- Exactitud absoluta
- Equivale a 58 inex más 9 saros (un saros más que un Immobilis), por lo tanto 1841 años 1 mes o 22771 lunaciones, que actualmente es aproximadamente una hora más que un número entero de semanas, lo que permite que los eclipses ocurran el mismo día de la semana. Debido a la desaceleración de la rotación de la Tierra, la duración de la Accuratissima será exactamente igual a un número entero de días o semanas alrededor del año 2100 d. C., lo que significa que un eclipse alrededor del año 1200 d. C. se repetirá a la misma hora del día en el mismo día de la semana 1841 años después. La Accuratissima también es útil para calcular la magnitud y el carácter de los eclipses. [3] Una Accuratissima más un Tritrix más un saros hace que un ciclo de eclipse sea 1,8 días más corto que 2000 años julianos, o 13,2 días más largo que 2000 años gregorianos. Es sólo medio día menos que un número entero de meses anómalos, mientras que el Accuratisssima sólo tiene 0,2 días menos que un número entero de meses anómalos.
- Ciclo de Mackay
- Equivale a 76 inex más 9 saros, es decir, 2362 años y aproximadamente un mes, siempre en el mismo nodo. Mencionado por A. Mackay en el siglo XIX. [3]
- Relojería
- Equivale a 110 inex más 7 saros, por lo tanto 3310 años y aproximadamente 2 meses, y siempre ocurre en el mismo nodo. Es útil para calcular el tiempo y la magnitud de los eclipses, ya que están separados por aproximadamente un número entero de meses y semanas dracónicos y anomalísticos (172.715,97 semanas), lo que da lugar a eclipses similares en carácter y tiempo de semanas. [3]
Serie Saros y serie Inex


Cualquier eclipse puede asignarse a una serie determinada de Saros y a una serie de Inex . El año de un eclipse solar (en el calendario gregoriano ) se obtiene aproximadamente mediante: [19]
- año = 28,945 × número de la serie saros + 18,030 × número de la serie inex − 2882,55
Cuando es mayor que 1, la parte entera da el año d.C., pero cuando es negativo el año a.C. se obtiene tomando la parte entera y sumando 2. Por ejemplo, el eclipse en la serie saros 0 y la serie inex 0 fue a mediados del 2884 a.C.
Luca Quaglia y John Tilley han elaborado un "panorama" de eclipses solares organizados por saros e inex que muestra 61775 eclipses solares desde 11001 a. C. hasta 15000 d. C. (ver más abajo). [20] Cada columna del gráfico es una serie completa de Saros que progresa suavemente desde eclipses parciales a eclipses totales o anulares y de nuevo a parciales. Cada fila del gráfico representa una serie inex. Dado que un saros, de 223 meses sinódicos, es ligeramente menos que un número entero de meses dracónicos, los eclipses tempranos en una serie de saros (en la parte superior del diagrama) ocurren después de que la Luna pase por su nodo (el comienzo y el final de un mes dracónico), mientras que los eclipses posteriores (en la parte inferior) ocurren antes de que la Luna pase por su nodo. Cada 18 años, el eclipse ocurre en promedio alrededor de medio grado más al oeste con respecto al nodo, pero la progresión no es uniforme.
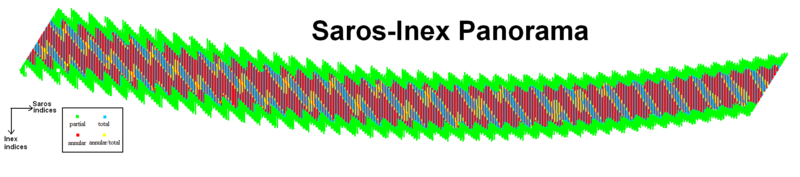

Se pueden calcular los números Saros e inex para un eclipse cercano a una fecha determinada. También se puede encontrar la fecha aproximada de los eclipses solares en fechas distantes determinando primero uno en una serie inex, como la serie 50. Esto se puede hacer sumando o restando algún múltiplo de 28,9450 años gregorianos al eclipse solar del 10 de mayo de 2013, o 28,9444 años julianos a la fecha juliana del 27 de abril de 2013. Una vez que se haya encontrado un eclipse de este tipo, se pueden encontrar otros en torno a la misma fecha utilizando los ciclos cortos. Para los eclipses lunares, se pueden utilizar las fechas de anclaje del 4 de mayo de 2004 o del 21 de abril juliano.
Los números saros e inex también se definen para los eclipses lunares. Un eclipse solar de una serie determinada de saros e inex será precedido quince días antes por un eclipse lunar cuyo número saros sea 26 menor y cuyo número inex sea 18 mayor, o será seguido quince días después por un eclipse lunar cuyo número saros sea 12 mayor y cuyo número inex sea 43 menor. Al igual que con los eclipses solares, el año gregoriano de un eclipse lunar se puede calcular como:
- año = 28,945 × número de la serie saros + 18,030 × número de la serie inex − 2454,564
Los eclipses lunares también se pueden representar en un diagrama similar, que abarca desde el año 1000 d. C. hasta el año 2500 d. C. La banda diagonal amarilla representa todos los eclipses desde el año 1900 hasta el año 2100. Este gráfico muestra de inmediato que este período de 1900 a 2100 contiene una cantidad de eclipses lunares totales superior a la media en comparación con otros siglos adyacentes.

Esto está relacionado con el hecho de que las tétradas (ver arriba) son más comunes en la actualidad que en otros períodos. Las tétradas ocurren cuando cuatro eclipses lunares ocurren en cuatro números inex lunares, decrecientes en 8 (es decir, con un semestre de diferencia), que están en el rango que da eclipses bastante centrales ( gamma pequeño ), y además los eclipses tienen lugar aproximadamente a mitad de camino entre el perihelio y el afelio de la Tierra. Por ejemplo, en la tétrada de 2014-2015 (las llamadas Cuatro Lunas de Sangre ), los números inex fueron 52, 44, 36 y 28, y los eclipses ocurrieron en abril y finales de septiembre-principios de octubre. Normalmente, el valor absoluto de gamma disminuye y luego aumenta, pero debido a que en abril el Sol está más al este que su longitud media , y en septiembre/octubre más al oeste que su longitud media, los valores absolutos de gamma en el primer y cuarto eclipse disminuyen, mientras que los valores absolutos en el segundo y tercero aumentan. El resultado es que los cuatro valores gamma son lo suficientemente pequeños como para provocar eclipses lunares totales. El fenómeno de la "alcanzamiento" de la Luna con el Sol (o el punto opuesto al Sol), que normalmente no está en su longitud media, se ha denominado "persecución severa". [21]
Las series inex se mueven lentamente a lo largo del año, y cada eclipse ocurre unos 20 días antes, 29 años después. Esto significa que, a lo largo de un período de 18,2 ciclos inex (526 años), la fecha se mueve a lo largo de todo el año. Pero, como el perihelio de la órbita de la Tierra también se mueve lentamente, las series inex que ahora están produciendo tétradas volverán a estar a medio camino entre el perihelio y el afelio de la Tierra en unos 586 años. [14]

Se puede inclinar el gráfico de inex versus saros para eclipses solares o lunares de modo que el eje x muestre la época del año. (Un eclipse que se produce dos series de saros y una serie de inex después de otro se producirá solo 1,8 días después en el año en el calendario gregoriano). Esto muestra las oscilaciones de 586 años como oscilaciones que ascienden alrededor del perihelio y descienden alrededor del afelio (ver gráfico).
Propiedades de los eclipses
Las propiedades de los eclipses, como el momento, la distancia o el tamaño de la Luna y el Sol, o la distancia que pasa la Luna al norte o al sur de la línea que separa el Sol de la Tierra, dependen de los detalles de las órbitas de la Luna y la Tierra. Existen fórmulas para calcular la longitud, la latitud y la distancia de la Luna y del Sol utilizando las series de senos y cosenos. Los argumentos de las funciones seno y coseno dependen únicamente de cuatro valores, los argumentos de Delaunay:
- D, la elongación media (ángulo entre las longitudes del Sol y la Luna)
- F, el argumento medio de latitud (el ángulo entre la Luna y el nodo ascendente)
- l, la anomalía media de la Luna (qué tan lejos está la Luna del perigeo)
- l', la anomalía media del Sol (o de la Tierra)
Estos cuatro argumentos son básicamente funciones lineales del tiempo pero con términos de orden superior que varían lentamente. Un diagrama de índices inex y saros como el "Panorama" que se muestra arriba es como un mapa, y podemos considerar los valores de los argumentos de Delaunay en él. La elongación media, D, recorre 360° 223 veces cuando el valor inex aumenta en 1, y 358 veces cuando el valor saros aumenta en 1. Por lo tanto, es equivalente a 0°, por definición, en cada combinación del índice solar saros y el índice inex, porque los eclipses solares ocurren cuando la elongación es cero. A partir de D se puede encontrar el tiempo transcurrido real a partir de algún tiempo de referencia como J2000 , que es como una función lineal de inex y saros pero con una desviación que crece cuadráticamente con la distancia desde el tiempo de referencia, que asciende a unos 19 minutos a una distancia de 1000 años. El argumento medio de latitud, F, es equivalente a 0° o 180° (dependiendo de si el índice saros es par o impar) a lo largo de la curva suave que pasa por el centro de la banda de eclipses, donde gamma es cercano a cero (alrededor de la serie inex 50 en la actualidad). F disminuye a medida que nos alejamos de esta curva hacia series inex más altas, y aumenta en el otro lado, en aproximadamente 0,5° por serie inex. Cuando el valor inex está demasiado lejos del centro, los eclipses desaparecen porque la Luna está demasiado al norte o al sur del Sol. La anomalía media del Sol es una función suave, que aumenta aproximadamente 10° cuando se aumenta inex en 1 en una serie saros y disminuye aproximadamente 20° cuando se aumenta el índice saros en 1 en una serie inex. Esto significa que es casi constante cuando se aumenta inex en 1 y el índice saros en 2 (el intervalo "Unidos" de 65 años). El gráfico anterior, que muestra la época del año en que se producen los eclipses, muestra básicamente la anomalía solar, ya que el perihelio se mueve sólo un día por siglo en el calendario juliano, o 1,7 días por siglo en el calendario gregoriano. La anomalía media de la Luna es más complicada. Si observamos los eclipses cuyo índice saros es divisible por 3, entonces la anomalía media es una función suave de los valores inex y saros. Los contornos se extienden en un ángulo, de modo que la anomalía media es bastante constante cuando los valores inex y saros aumentan juntos en una proporción de alrededor de 21:24. La función varía lentamente, cambiando sólo 7,4° cuando se cambia el índice saros por 3 con un valor inex constante. Una función suave similar se obtiene para los eclipses con saros módulo 3 igual a 1, pero desplazado unos 120°, y para saros módulo 3 igual a 2, desplazado 120° en sentido contrario. [22] [23]

El resultado es que las propiedades varían lentamente a lo largo del diagrama en cualquiera de los tres conjuntos de series de Saros. El gráfico adjunto muestra solo las series de Saros que tienen un índice de Saros módulo 3 igual a cero. Las áreas azules son donde la anomalía media de la Luna está cerca de 0°, lo que significa que la Luna está cerca del perigeo en el momento del eclipse y, por lo tanto, es relativamente grande, lo que favorece los eclipses totales. En el área roja, la Luna generalmente está más lejos de la Tierra y los eclipses son anulares. También podemos ver el efecto de la anomalía del Sol. Los eclipses en julio, cuando el Sol está más lejos de la Tierra, tienen más probabilidades de ser totales, por lo que el área azul se extiende sobre un rango mayor de índice de inex que para los eclipses en enero.
La ondulación que se observa en el gráfico también se debe a la anomalía del Sol. En abril, el Sol está más al este que si su longitud progresara uniformemente, y en octubre está más al oeste, y esto significa que en abril la Luna alcanza al Sol relativamente tarde, y en octubre relativamente temprano. Esto a su vez significa que el argumento de latitud en el momento real del eclipse se elevará más en abril y se reducirá en octubre. Los eclipses (ya sean parciales o no) con un índice inex bajo (cerca del borde superior en el gráfico "Panorama") no ocurren en abril porque la sicigia ocurre demasiado al este del nodo, pero ocurren más eclipses con valores inex altos en abril porque la sicigia no está tan al oeste del nodo. Lo opuesto se aplica a octubre. También significa que en abril los eclipses solares de nodo ascendente proyectarán su sombra más al norte (como el eclipse solar del 8 de abril de 2024 ), y los eclipses de nodo descendente más al sur. Lo opuesto es el caso en octubre.
Los eclipses que ocurren cuando la Tierra está cerca del perihelio (anomalía solar cercana a cero) se encuentran en la serie de Saros, en la que el valor gamma cambia poco cada 18,03 años. La razón de esto es que de un eclipse al siguiente en la serie de Saros, el día del año avanza unos 11 días, pero la posición del Sol se mueve hacia el este más de lo que lo hace para ese cambio de día en el año en otros momentos. Esto significa que la posición del Sol en relación con el nodo no cambia tanto como para las series de Saros que dan eclipses en otros momentos del año. En la primera mitad del siglo XXI, las series de Saros solares que muestran esta lenta tasa de cambio de gamma incluyen 122 (que da un eclipse el 6 de enero de 2019), 132 (5 de enero de 2038), 141 (15 de enero de 2010) y 151 (4 de enero de 2011). A veces este fenómeno lleva a que una serie de saros produzca un gran número de eclipses centrales; por ejemplo, el saros solar 128 produjo 20 eclipses con |γ|<0,75 entre 1615 y 1958, mientras que la serie 135 produjo solo nueve, entre 1872 y 2016. [14]


El intervalo de tiempo entre dos eclipses en un ciclo de eclipses es variable. El tiempo de un eclipse puede adelantarse o retrasarse hasta diez horas debido a la excentricidad de la órbita de la Luna: el eclipse será temprano cuando la Luna esté pasando del perigeo al apogeo, y tarde cuando esté pasando del apogeo al perigeo. El tiempo también se retrasa debido a la excentricidad de la órbita de la Tierra. Los eclipses ocurren aproximadamente cuatro horas más tarde en abril y cuatro horas antes en octubre. Esto significa que el retraso varía de un eclipse a otro en una serie. El retraso es la suma de dos funciones de tipo seno, una basada en el tiempo en el año anomalístico y otra en el tiempo en el mes anomalístico. Los períodos de estas dos ondas dependen de lo cerca que esté el intervalo nominal entre dos eclipses en la serie de un número entero de años anomalísticos y meses anomalísticos. En series como la "Immobilis" o la "Accuratissima", que son casi números enteros de ambas, el retraso varía muy lentamente, por lo que el intervalo es bastante constante. En series como el octón, la anomalía de la Luna cambia considerablemente al menos dos veces cada tres intervalos, por lo que los intervalos varían considerablemente.
El "Panorama" también puede estar relacionado con el lugar de la Tierra donde cae la sombra de la Luna en el momento central del eclipse. Si este "eclipse máximo" para un eclipse dado se produce en un lugar determinado, los eclipses que se produzcan tres saros después se producirán en una latitud (porque el saros está cerca de un número entero de meses dracónicos) y una longitud (porque un período de tres saros siempre está a un par de horas de tener una duración de 19755,96 días, lo que cambiaría la longitud en unos 13° hacia el este). Si, en cambio, aumentamos el índice saros a un índice inex constante, los intervalos son bastante variables porque el número de meses o años anómalos no está muy cerca de un número entero. Esto significa que, aunque la latitud será similar (pero cambiará de signo), el cambio de longitud puede variar en más de 180°. Un movimiento de seis inex (un ciclo de De la Hire) conserva bastante bien la latitud, pero el cambio de longitud es muy variable debido a la variación de la anomalía solar.

Tanto el tamaño angular de la Luna en el cielo durante los eclipses en el nodo ascendente como el tamaño del Sol en esos eclipses varían en una especie de onda sinusoidal. Los tamaños en el nodo descendente varían de la misma manera, pero con un desfase de 180°. La Luna es grande en un eclipse en el nodo ascendente cuando su perigeo está cerca del nodo ascendente, por lo que el período para el tamaño de la Luna es el tiempo que tarda el ángulo entre el nodo y el perigeo en recorrer 360°, o
- años
(Tenga en cuenta que se utiliza un signo más porque el perigeo se mueve hacia el este mientras que el nodo se mueve hacia el oeste). Un máximo de esto es en 2024 (septiembre), lo que explica por qué el eclipse solar del nodo ascendente del 8 de abril de 2024 está cerca del perigeo y es total y el eclipse solar del nodo descendente del 2 de octubre de 2024 está cerca del apogeo y es anular. Aunque este ciclo es aproximadamente un día menos que seis años, los eclipses de superluna en realidad ocurren cada tres años en promedio, porque también hay eclipses en el nodo descendente que ocurren entre los del nodo ascendente. En los eclipses lunares, el tamaño de la Luna está desfasado 180° con su tamaño en los eclipses solares.
El Sol es grande en un eclipse de nodo ascendente cuando su perigeo (la dirección hacia el Sol cuando está más cerca de la Tierra) está cerca del nodo ascendente, por lo que el período para el tamaño del Sol es
- años
En términos de los argumentos de Delaunay, el Sol es más grande en los eclipses solares de nodo ascendente y más pequeño en los eclipses solares de nodo descendente alrededor de cuando l'+D=F (módulo 360°), como en junio de 2010. Es más pequeño en los eclipses solares de nodo descendente y más grande en los eclipses solares de nodo ascendente 9,3 años después, como en septiembre de 2019.
Tendencias a largo plazo
La duración de los meses sinódicos, dracónicos y anomalísticos, la duración del día y la duración del año anomalístico están cambiando lentamente. Los meses sinódicos y dracónicos, el día y el año anomalístico (al menos en la actualidad) se están haciendo más largos, mientras que el mes anomalístico se está acortando. La excentricidad de la órbita de la Tierra está disminuyendo actualmente a un ritmo de aproximadamente un uno por ciento cada 300 años, lo que disminuye el efecto de la anomalía del sol. Las fórmulas para los argumentos de Delaunay muestran que el alargamiento del mes sinódico significa que los eclipses tienden a ocurrir más tarde de lo que ocurrirían de otra manera proporcionalmente al cuadrado de la separación temporal a partir de ahora, en aproximadamente 0,32 horas por milenio al cuadrado. Los demás argumentos de Delaunay (la anomalía media de la Luna y del Sol y el argumento de la latitud) se verán reforzados por este motivo, pero, por otra parte, los argumentos de Delaunay también se ven afectados por el hecho de que las duraciones del mes dracónico y del mes y año anomalísticos están cambiando. Los resultados netos son:
- El argumento medio de latitud se reduce en 0,16° por milenio al cuadrado, lo que corresponde a 0,00045 meses dracónicos.
- La anomalía media de la Luna aumenta en 1,1° por milenio al cuadrado, lo que corresponde a 0,0030 meses anomalísticos.
- La anomalía media del Sol disminuye en 0,002° por milenio al cuadrado, lo que es bastante insignificante.
Por ejemplo, desde el eclipse solar de abril de 1688 a. C. hasta el de abril de 1623 d. C., hay 110 inex más 7 saros (equivalentes a una "Palaea-Horologia" más una "tritrix", 3310,09 años julianos). Según la tabla anterior, los argumentos de Delaunay deberían cambiar de la siguiente manera:
- 40941 meses sinódicos, 44429.003 meses dracónicos, 43877.032 meses anómalos, 3310.007 años anómalos, resp.
Pero debido a los cambios en la longitud de estos, en realidad cambiaron en: [22]
- 40940.998 meses sinódicos, 44429.006 meses dracónicos, 43876.990 meses anómalos, 3310.007 años anómalos, resp.
Obsérvese que en este ejemplo, en términos de anomalía (posición con respecto al perigeo), la luna regresa al 1% de una órbita (aproximadamente 3,4°), en lugar del 3,2% como se predijo utilizando los valores actuales de la duración de los meses.
El hecho de que el día se esté haciendo más largo significa que hay más revoluciones de la Tierra desde algún punto en el pasado de lo que uno podría calcular a partir de la hora y la fecha, y menos desde ahora hasta algún momento futuro. Este efecto significa que los eclipses ocurren antes en el día o calendario, yendo en la dirección opuesta en relación con el efecto del alargamiento del mes sinódico ya mencionado. Este efecto se conoce como ΔT . No se puede calcular con exactitud, pero asciende a alrededor de 50 minutos por milenio al cuadrado. [24] En nuestro ejemplo anterior, esto significa que aunque el eclipse en 1688 a. C. estaba centrado el 16 de marzo a las 00:15:31 en tiempo dinámico , en realidad ocurrió antes de la medianoche y, por lo tanto, el 15 de marzo (usando el tiempo basado en la ubicación del Greenwich actual y usando el calendario juliano proléptico ). [25]
El hecho de que el argumento de latitud sea menor explica por qué se ve una curvatura en el "Panorama" de arriba. Los eclipses centrales en el pasado y en el futuro son más altos en el gráfico (número inex más bajo) de lo que se esperaría de una extrapolación lineal. Esto se debe a que la relación entre la duración de un mes sinódico y la duración de un mes dracónico se está haciendo más pequeña. Aunque ambos se están haciendo más largos, el mes dracónico lo está haciendo más rápidamente porque la velocidad a la que el nodo se mueve hacia el oeste está disminuyendo. [22]
Véase también
Referencias
- ^ propiamente, se trata de períodos, no de ciclos
- ^ abc NASA Periodicidad de los eclipses solares
- ^ abcdefghijklmnopqrstu vwxyz aa ab ac ad ae af ag ah ai aj ak Rob van Gent. "Un catálogo de ciclos de eclipses". Universidad de Utrecht.
- ^ Eclipses solares: 2011-2020
- ^ Littmann, Mark; Fred Espenak; Ken Willcox (2008). Totalidad: Eclipses de Sol . Oxford University Press. ISBN 978-0-19-953209-4.
- ^ Periodicidad de los eclipses lunares y solares, Fred Espenak
- ^ Catálogo de eclipses lunares y solares de cinco milenios: -1999 a +3000, Fred Espenak y Jean Meeus
- ^ Meeus (1991) forma. 47.1
- ^ Meeus (1991) cap. 49 pág. 334
- ^ Meeus (1991) forma. 48.1
- ^ 2,170391682 = 2 + 0,170391682 ; 1/0,170391682 = 5 + 0,868831085... ; 1/0,868831085... = 1 +5097171...6237575... ; etc. ; Evaluando esta cuarta fracción continua: 1/6 + 1 = 7/6; 6/7 + 5 = 41/7 ; 7/41 + 2 = 89/41
- ^ de Giovanni Valsecchi, Ettore Perozzi, Archie Roy, Bonnie Steves (marzo de 1993). "Órbitas periódicas cercanas a la de la Luna". Astronomía y Astrofísica : 311.
{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace ) - ^ ab Ver Panorama de Quaglia y Tilley.
- ^ abcd John H. Duke (20 de mayo de 2010). "¿Las consolidaciones periódicas de las contracorrientes del Pacífico desencadenan un enfriamiento global mediante un fenómeno de La Niña simétrico en el ecuador?" (PDF) . Climate of the Past Discussions . 6 (3): 928–929. Bibcode :2010CliPD...6..905D. doi : 10.5194/cpd-6-905-2010 .Véanse especialmente las figuras 10 y 13.
- ^ Boletín SE de febrero de 1999,
- ^¿ Con qué frecuencia ocurre un eclipse solar en el equinoccio de marzo?
- ^ Vidas eminentes en la ciencia y la religión del siglo XX,
- ^ Ciclo de eclipse de 29 años,
- ^ Basado en los ciclos Saros, Inex y Eclipse.
- ^ Panorama de Saros-Inex. Datos en eclipse solar panaorama.xls.
- ^ John H. Duke (20 de mayo de 2010). "¿Las consolidaciones periódicas de las contracorrientes del Pacífico desencadenan un enfriamiento global mediante un fenómeno de La Niña simétrico en el ecuador?" (PDF) . Climate of the Past Discussions . 6 (3): 905. Bibcode :2010CliPD...6..905D. doi : 10.5194/cpd-6-905-2010 .Véase también Fergus Wood (1976). El papel estratégico de las mareas vivas de perigeo en la historia náutica y las inundaciones costeras de América del Norte, 1635-1976.
- ^ abc Jean-Louis Simon; et al. (1994). "Expresiones numéricas para fórmulas de precesión y elementos medios para la Luna y los planetas" (PDF) . Astronomía y Astrofísica . Bibcode :1994A&A...282..663S.
- ^ TC van Flandern y KF Pulkkinen (1979). "Fórmulas de baja precisión para posiciones planetarias" (PDF) . Serie de suplementos de revistas astrofísicas . Código Bibliográfico :1979ApJS...41..391V.
- ^ Basado en la duración de un siglo aumentando en 62 segundos por siglo (ver ΔT (cronometraje) ).
- ^ Fred Espenak. "Catálogo de eclipses solares de cinco milenios -1699 a -1600 (1700 a. C. a 1601 a. C.)". Sitio web de la NASA sobre eclipses .El Tiempo Universal de momentos dados de un eclipse es diferente del Tiempo de Efemérides dado por los cálculos – véase p. 59 de Schaefer, BE (marzo de 1990). Visibilidad lunar y la crucifixión. Royal Astronomical Society Quarterly Journal, 31(1), 53–67.
- S. Newcomb (1882): Sobre la recurrencia de los eclipses solares. Astron.Pap.Am.Eph. vol. I pt. I. Oficina de Navegación, Departamento de la Marina, Washington 1882
- JN Stockwell (1901): Ciclos eclipsarios. Astron.J. 504 [vol.xx1(24)], 14 de agosto de 1901
- ACD Crommelin (1901): El ciclo de eclipses de 29 años. Observatorio xxiv n.° 310, 379, oct. 1901
- A. Pannekoek (1951): Periodicidades de los eclipses lunares. Proc. Kon. Ned. Acad. Wetensch. Ser.B vol.54 págs.30..41 (1951)
- G. van den Bergh (1954): Eclipses en el segundo milenio antes de Cristo Tjeenk Willink & Zn NV, Haarlem 1954
- G. van den Bergh (1955): Periodicidad y variación de los eclipses solares (y lunares), 2 vols. Tjeenk Willink & Zn NV, Haarlem 1955
- Jean Meeus (1991): Algoritmos astronómicos (1ª ed.). Willmann-Bell, Richmond VA 1991; ISBN 0-943396-35-2
- Jean Meeus (1997): Fragmentos de astronomía matemática [I], cap. 9 Eclipses solares: algunas periodicidades (págs. 49 a 55). Willmann-Bell, Richmond VA 1997; ISBN 0-943396-51-4
- Jean Meeus (2004): Bocados de astronomía matemática III, capítulo 21 Tétradas lunares (págs. 123..140). Willmann-Bell, Richmond VA 2004; ISBN 0-943396-81-6
Enlaces externos
- Un catálogo de ciclos de eclipses (más completo que el anterior)
- Busque 5000 años de eclipses entre el año 2000 a. C. y el año 3000 d. C.
- Los eclipses, el reloj cósmico de los antiguos
- Los Saros y el Inex


