Pseudobosque

En teoría de grafos , un pseudobosque es un grafo no dirigido ^[1] en el que cada componente conexo tiene como máximo un ciclo . Es decir, es un sistema de vértices y aristas que conectan pares de vértices, de modo que ningún par de ciclos de aristas consecutivas comparten ningún vértice entre sí, ni ningún par de ciclos pueden estar conectados entre sí por un camino de aristas consecutivas. Un pseudoárbol es un pseudobosque conexo.

Los nombres se justifican por analogía con los árboles y bosques más comúnmente estudiados . (Un árbol es un gráfico conectado sin ciclos; un bosque es una unión disjunta de árboles). Gabow y Tarjan ^[2] atribuyen el estudio de los pseudobosques al libro de Dantzig de 1963 sobre programación lineal , en el que los pseudobosques surgen en la solución de ciertos problemas de flujo de red . ^[3] Los pseudobosques también forman modelos de funciones en teoría de grafos y ocurren en varios problemas algorítmicos . Los pseudobosques son grafos dispersos - su número de aristas está linealmente limitado en términos de su número de vértices (de hecho, tienen como máximo tantas aristas como vértices) - y su estructura matroide permite que varias otras familias de grafos dispersos se descompongan como uniones de bosques y pseudobosques. El nombre "pseudobosque" proviene de Picard y Queyranne (1982).

Definimos un grafo no dirigido como un conjunto de vértices y aristas de modo que cada arista tiene dos vértices (que pueden coincidir) como puntos finales. Es decir, permitimos múltiples aristas (aristas con el mismo par de puntos finales) y bucles (aristas cuyos dos puntos finales son el mismo vértice). ^[1] Un subgrafo de un grafo es el grafo formado por cualquier subconjunto de sus vértices y aristas de modo que cada arista en el subconjunto de aristas tenga ambos puntos finales en el subconjunto de vértices. Un componente conexo de un grafo no dirigido es el subgrafo que consiste en los vértices y aristas a los que se puede llegar siguiendo las aristas desde un único vértice inicial dado. Un grafo es conexo si cada vértice o arista es alcanzable desde todos los demás vértices o aristas. Un ciclo en un grafo no dirigido es un subgrafo conexo en el que cada vértice incide exactamente en dos aristas, o es un bucle. ^[4]

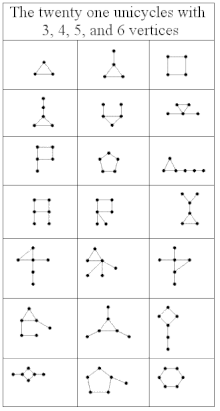
Un pseudobosque es un grafo no dirigido en el que cada componente conexo contiene como máximo un ciclo. ^[5] Equivalentemente, es un grafo no dirigido en el que cada componente conexo no tiene más aristas que vértices. ^[6] Los componentes que no tienen ciclos son simplemente árboles , mientras que los componentes que tienen un solo ciclo dentro de ellos se denominan 1-árboles o grafos unicíclicos . Es decir, un 1-árbol es un grafo conexo que contiene exactamente un ciclo. Un pseudobosque con un solo componente conexo (normalmente llamado pseudoárbol , aunque algunos autores definen un pseudoárbol como un 1-árbol) es o bien un árbol o bien un 1-árbol; en general, un pseudobosque puede tener múltiples componentes conexos siempre que todos ellos sean árboles o 1-árboles.

Si se elimina de un árbol 1 una de las aristas de su ciclo, el resultado es un árbol. Invirtiendo este proceso, si se aumenta un árbol conectando dos de sus vértices mediante una nueva arista, el resultado es un árbol 1; el camino en el árbol que conecta los dos puntos finales de la arista añadida, junto con la arista añadida misma, forman el ciclo único del árbol 1. Si se aumenta un árbol 1 añadiendo una arista que conecta uno de sus vértices con un vértice recién añadido, el resultado es de nuevo un árbol 1, con un vértice más; un método alternativo para construir árboles 1 es empezar con un único ciclo y luego repetir esta operación de aumento cualquier número de veces. Las aristas de cualquier árbol 1 se pueden dividir de forma única en dos subgrafos, uno de los cuales es un ciclo y el otro es un bosque, de modo que cada árbol del bosque contenga exactamente un vértice del ciclo. ^[7]

También se han estudiado ciertos tipos más específicos de pseudobosques.

Un 1-bosque , a veces llamado pseudobosque máximo , es un pseudobosque al que no se pueden agregar más aristas sin provocar que algún componente del grafo contenga múltiples ciclos. Si un pseudobosque contiene un árbol como uno de sus componentes, no puede ser un 1-bosque, ya que se puede agregar una arista que conecte dos vértices dentro de ese árbol, formando un solo ciclo, o una arista que conecte ese árbol con algún otro componente. Por lo tanto, los 1-bosques son exactamente los pseudobosques en los que cada componente es un 1-árbol.

Los pseudobosques que abarcan un grafo no dirigido G son los subgrafos pseudobosque de G que tienen todos los vértices de G. Un pseudobosque de este tipo no necesita tener aristas, ya que, por ejemplo, el subgrafo que tiene todos los vértices de G y ninguna arista es un pseudobosque (cuyos componentes son árboles que constan de un único vértice).

Los pseudobosques máximos de G son los subgrafos de pseudobosques de G que no están contenidos dentro de ningún pseudobosque mayor de G. Un pseudobosque máximo de G es siempre un pseudobosque que se expande, pero no a la inversa. Si G no tiene componentes conectados que sean árboles, entonces sus pseudobosques máximos son 1-bosques, pero si G tiene un componente de árbol, sus pseudobosques máximos no son 1-bosques. Dicho de manera precisa, en cualquier grafo G sus pseudobosques máximos consisten en cada componente de árbol de G , junto con uno o más 1-árboles disjuntos que cubren los vértices restantes de G.

También se utilizan versiones de estas definiciones para grafos dirigidos . Al igual que un grafo no dirigido, un grafo dirigido consta de vértices y aristas, pero cada arista está dirigida desde uno de sus puntos finales al otro punto final. Un pseudobosque dirigido es un grafo dirigido en el que cada vértice tiene como máximo una arista saliente; es decir, tiene un grado de salida como máximo uno. Un 1-bosque dirigido , más comúnmente llamado grafo funcional (ver más abajo), a veces pseudobosque dirigido maximalista , es un grafo dirigido en el que cada vértice tiene un grado de salida exactamente uno. ^[8] Si D es un pseudobosque dirigido, el grafo no dirigido formado al eliminar la dirección de cada arista de D es un pseudobosque no dirigido.

Cada pseudobosque sobre un conjunto de n vértices tiene como máximo n aristas, y cada pseudobosque maximal sobre un conjunto de n vértices tiene exactamente n aristas. Por el contrario, si un grafo G tiene la propiedad de que, para cada subconjunto S de sus vértices, el número de aristas en el subgrafo inducido de S es como máximo el número de vértices en S , entonces G es un pseudobosque. Los 1-árboles pueden definirse como grafos conexos con la misma cantidad de vértices y aristas. ^[2]

Pasando de los grafos individuales a las familias de grafos, si una familia de grafos tiene la propiedad de que cada subgrafo de un grafo en la familia también está en la familia, y cada grafo en la familia tiene como máximo tantas aristas como vértices, entonces la familia contiene solo pseudobosques. Por ejemplo, cada subgrafo de un thrackle (un grafo dibujado de modo que cada par de aristas tenga un punto de intersección) también es un thrackle, por lo que la conjetura de Conway de que cada thrackle tiene como máximo tantas aristas como vértices puede reformularse diciendo que cada thrackle es un pseudobosque. Una caracterización más precisa es que, si la conjetura es verdadera, entonces los thrackles son exactamente los pseudobosques sin ciclo de cuatro vértices y como máximo un ciclo impar. ^[9]

Streinu y Theran ^[10] generalizan las condiciones de escasez que definen a los pseudobosques: definen un grafo como ( k , l )-disperso si cada subgrafo no vacío con n vértices tiene como máximo kn  −  l aristas, y ( k , l )-estrecho si es ( k , l )-disperso y tiene exactamente kn  −  l aristas. Por lo tanto, los pseudobosques son los grafos (1,0)-dispersos, y los pseudobosques máximos son los grafos (1,0)-estrechos. Se pueden definir varias otras familias importantes de grafos a partir de otros valores de k y l , y cuando l  ≤  k los grafos ( k , l )-dispersos se pueden caracterizar como los grafos formados como la unión disjunta de aristas de l bosques y k  −  l pseudobosques. ^[11]

Casi todo grafo aleatorio suficientemente disperso es un pseudobosque. ^[12] Es decir, si c es una constante con 0 < c < 1/2, y P _c ( n ) es la probabilidad de que elegir uniformemente al azar entre los grafos de n vértices con cn aristas resulte en un pseudobosque, entonces P _c ( n ) tiende a uno en el límite para n grande . Sin embargo, para c > 1/2, casi todo grafo aleatorio con cn aristas tiene un componente grande que no es unicíclico.

Un grafo es simple si no tiene bucles propios ni múltiples aristas con los mismos puntos finales. La cantidad de árboles 1 simples con n vértices etiquetados es ^[13]

${\displaystyle n\sum _{k=1}^{n}{\frac {(-1)^{k-1}}{k}}\sum _{n_{1}+\cdots +n_{k}=n}{\frac {n!}{n_{1}!\cdots n_{k}!}}{\binom {{\binom {n_{1}}{2}}+\cdots +{\binom {n_{k}}{2}}}{n}}.}$

Los valores para n hasta 300 se pueden encontrar en la secuencia OEIS : A057500 de la Enciclopedia en línea de secuencias enteras .

El número de pseudobosques dirigidos máximos en n vértices, que permiten bucles propios, es n ⁿ , porque para cada vértice hay n puntos finales posibles para el borde saliente. André Joyal utilizó este hecho para proporcionar una prueba biyectiva de la fórmula de Cayley , de que el número de árboles no dirigidos en n nodos es n ^{n  − 2} , al encontrar una biyección entre pseudobosques dirigidos máximos y árboles no dirigidos con dos nodos distinguidos. ^[14] Si no se permiten bucles propios, el número de pseudobosques dirigidos máximos es en cambio ( n  − 1) ⁿ .

Los pseudobosques dirigidos y las endofunciones son, en cierto sentido, matemáticamente equivalentes. Cualquier función ƒ de un conjunto X hacia sí mismo (es decir, un endomorfismo de X ) puede interpretarse como la definición de un pseudobosque dirigido que tiene una arista de x a y siempre que ƒ( x ) = y . El pseudobosque dirigido resultante es máximo y puede incluir bucles propios siempre que algún valor x tenga ƒ( x ) = x . Alternativamente, omitir los bucles propios produce un pseudobosque no máximo. En la otra dirección, cualquier pseudobosque dirigido máximo determina una función ƒ tal que ƒ( x ) sea el objetivo de la arista que sale de x , y cualquier pseudobosque dirigido no máximo puede hacerse máximo añadiendo bucles propios y luego convertirse en una función de la misma manera. Por esta razón, los pseudobosques dirigidos máximos a veces se denominan grafos funcionales . ^[2] Ver una función como un gráfico funcional proporciona un lenguaje conveniente para describir propiedades que no son tan fáciles de describir desde el punto de vista de la teoría de funciones; esta técnica es especialmente aplicable a problemas que involucran funciones iteradas , que corresponden a caminos en gráficos funcionales.

La detección de ciclos , el problema de seguir una ruta en un gráfico funcional para encontrar un ciclo en él, tiene aplicaciones en criptografía y teoría de números computacionales , como parte del algoritmo rho de Pollard para la factorización de números enteros y como un método para encontrar colisiones en funciones hash criptográficas . En estas aplicaciones, se espera que ƒ se comporte de manera aleatoria; Flajolet y Odlyzko ^[15] estudian las propiedades de teoría de grafos de los gráficos funcionales que surgen de mapeos elegidos aleatoriamente. En particular, una forma de la paradoja del cumpleaños implica que, en un gráfico funcional aleatorio con n vértices, la ruta que comienza desde un vértice seleccionado aleatoriamente típicamente retrocederá sobre sí misma para formar un ciclo dentro de O( √ n ) pasos. Konyagin et al. han logrado avances analíticos y computacionales en las estadísticas de grafos. ^[16]

Martin, Odlyzko y Wolfram ^[17] investigan pseudobosques que modelan la dinámica de los autómatas celulares . Estos grafos funcionales, que ellos llaman diagramas de transición de estados , tienen un vértice para cada configuración posible en la que puede estar el conjunto de células del autómata, y una arista que conecta cada configuración con la configuración que la sigue según la regla del autómata. Se pueden inferir propiedades del autómata a partir de la estructura de estos diagramas, como el número de componentes, la longitud de los ciclos limitantes, la profundidad de los árboles que conectan los estados no limitantes con estos ciclos, o las simetrías del diagrama. Por ejemplo, cualquier vértice sin arista entrante corresponde a un patrón de Jardín del Edén y un vértice con un bucle propio corresponde a un patrón de naturaleza muerta .

Otra aplicación temprana de los grafos funcionales se encuentra en los trenes utilizados para estudiar los sistemas triples de Steiner . ^[18] El tren de un sistema triple es un grafo funcional que tiene un vértice para cada triple posible de símbolos; cada triple pqr se mapea mediante ƒ a stu , donde pqs , prt y qru son los triples que pertenecen al sistema triple y contienen los pares pq , pr y qr respectivamente. Se ha demostrado que los trenes son un invariante poderoso de los sistemas triples, aunque algo engorrosos de calcular.

Un matroide es una estructura matemática en la que ciertos conjuntos de elementos se definen como independientes , de tal manera que los conjuntos independientes satisfacen propiedades modeladas a partir de las propiedades de independencia lineal en un espacio vectorial . Uno de los ejemplos estándar de un matroide es el matroide gráfico en el que los conjuntos independientes son los conjuntos de aristas en los bosques de un grafo; la estructura matroide de los bosques es importante en los algoritmos para calcular el árbol de expansión mínimo del grafo. Análogamente, podemos definir matroides a partir de pseudobosques.

Para cualquier grafo G = ( V , E ), podemos definir un matroide en los bordes de G , en el que un conjunto de bordes es independiente si y solo si forma un pseudobosque; este matroide se conoce como el matroide bicircular (o matroide bicicleta ) de G . ^{[19] [20]} Los conjuntos dependientes más pequeños para este matroide son los subgrafos conexos mínimos de G que tienen más de un ciclo, y estos subgrafos a veces se denominan bicicletas. Hay tres tipos posibles de bicicleta: un grafo theta tiene dos vértices que están conectados por tres caminos internamente disjuntos, un grafo en forma de 8 consta de dos ciclos que comparten un solo vértice, y un grafo de esposas está formado por dos ciclos disjuntos conectados por un camino. ^[21] Un grafo es un pseudobosque si y solo si no contiene una bicicleta como subgrafo. ^[10]

La formación de un menor de un pseudobosque contrayendo algunos de sus bordes y eliminando otros produce otro pseudobosque. Por lo tanto, la familia de pseudobosques está cerrada bajo menores, y el teorema de Robertson-Seymour implica que los pseudobosques pueden caracterizarse en términos de un conjunto finito de menores prohibidos , de manera análoga al teorema de Wagner que caracteriza a los grafos planares como los grafos que no tienen ni el grafo completo K ₅ ni el grafo bipartito completo K _3,3 como menores. Como se discutió anteriormente, cualquier grafo que no sea pseudobosque contiene como subgrafo un grafo de esposas, figura 8 o theta; cualquier grafo de esposas o figura 8 puede contraerse para formar un grafo mariposa (figura 8 de cinco vértices), y cualquier grafo theta puede contraerse para formar un grafo diamante (grafo theta de cuatro vértices), ^[22] por lo que cualquier no pseudobosque contiene una mariposa o un diamante como menor, y estos son los únicos grafos no pseudobosques menores-minimalistas. Por lo tanto, un grafo es un pseudobosque si y solo si no tiene la mariposa o el rombo como menores. Si se prohíbe solo el rombo pero no la mariposa, la familia de grafos más grande resultante consta de los grafos de cactus y las uniones disjuntas de múltiples grafos de cactus. ^[23]

En términos más simples, si se consideran multigrafos con bucles propios , solo hay un menor prohibido: un vértice con dos bucles.

Un uso algorítmico temprano de los pseudobosques involucra el algoritmo de red simplex y su aplicación a problemas de flujo generalizados que modelan la conversión entre productos de diferentes tipos. ^{[3] [24]} En estos problemas, se da como entrada una red de flujo en la que los vértices modelan cada producto y los bordes modelan las conversiones permitidas entre un producto y otro. Cada borde está marcado con una capacidad (cuánto de un producto se puede convertir por unidad de tiempo), un multiplicador de flujo (la tasa de conversión entre productos) y un costo (cuánta pérdida o, si es negativo, ganancia se incurre por unidad de conversión). La tarea es determinar cuánto de cada producto se debe convertir a través de cada borde de la red de flujo, para minimizar el costo o maximizar la ganancia, al mismo tiempo que se obedecen las restricciones de capacidad y no se permite que los productos de ningún tipo se acumulen sin usar. Este tipo de problema se puede formular como un programa lineal y resolverse utilizando el algoritmo simplex . Las soluciones intermedias que surgen de este algoritmo, así como la solución óptima final, tienen una estructura especial: cada borde de la red de entrada no se utiliza o se utiliza a su máxima capacidad, excepto un subconjunto de los bordes, formando un pseudobosque que abarca la red de entrada, para el cual las cantidades de flujo pueden estar entre cero y la máxima capacidad. En esta aplicación, los grafos unicíclicos también se denominan a veces árboles aumentados y los pseudobosques máximos también se denominan a veces bosques aumentados . ^[24]

El problema del pseudobosque de expansión mínima implica encontrar un pseudobosque de expansión de peso mínimo en un grafo ponderado por aristas más grande G . Debido a la estructura matroide de los pseudobosques, se pueden encontrar pseudobosques máximos de peso mínimo mediante algoritmos voraces similares a los del problema del árbol de expansión mínima . Sin embargo, Gabow y Tarjan encontraron un enfoque de tiempo lineal más eficiente en este caso. ^[2]

La pseudoarboricidad de un grafo G se define por analogía con la arboricidad como el número mínimo de pseudobosques en los que se pueden dividir sus aristas; equivalentemente, es el k mínimo tal que G es ( k ,0)-escaso, o el k mínimo tal que las aristas de G se pueden orientar para formar un grafo dirigido con grado de salida como máximo k . Debido a la estructura matroide de los pseudobosques, la pseudoarboricidad se puede calcular en tiempo polinomial. ^[25]

Un grafo bipartito aleatorio con n vértices en cada lado de su bipartición, y con cn aristas elegidas independientemente al azar de cada uno de los n ² pares de vértices posibles, es un pseudobosque con alta probabilidad siempre que c sea una constante estrictamente menor que uno. Este hecho juega un papel clave en el análisis del algoritmo cuckoo hashing , una estructura de datos para buscar pares clave-valor buscando en una de dos tablas hash en ubicaciones determinadas a partir de la clave: se puede formar un grafo, el "grafo cuckoo", cuyos vértices corresponden a ubicaciones de la tabla hash y cuyas aristas unen las dos ubicaciones en las que se podría encontrar una de las claves, y el algoritmo cuckoo hashing logra encontrar ubicaciones para todas sus claves si y solo si el grafo cuckoo es un pseudobosque. ^[26]

Los pseudobosques también juegan un papel clave en algoritmos paralelos para la coloración de gráficos y problemas relacionados. ^[27]

• Weisstein, Eric W. , "Gráfico unicíclico", MathWorld